基于CEEMD和改進小波閾值法的鋼架結構沉降數據去噪方法

王民頓 尚俊娜

1 杭州電子科技大學通信工程學院，杭州市2號大街1158號,310018

近年來，隨著中國基礎建設的蓬勃發展，各種復雜的大型工程建筑體日益增多[1]，但施工條件和施工質量難以準確監測監控，高層建筑和大型設備設施坍塌事件時有發生，往往造成嚴重的人員傷亡和財產損失。如何減少這類事故的發生，已迫在眉睫。

形變數據監測是衡量建筑物結構安全穩定性的標尺[2]，所以大力開展形變實時監測系統以及險情預警研究勢在必行，這樣有利于施工人員及時發現施工建筑存在的隱患，進而提高建筑物的安全性。然而在實際監測過程中，由于受到各種外界因素的影響，形變監測數據往往存在不穩定因素，如存在許多跳變點和尖峰，以及各時段的數據之間存在非線性、隨機性[3]等情況，因此有必要關注沉降數據的去噪問題。

現今應用于形變監測的手段包括GNSS技術、常規大地測量、InSAR方法及其他專用測量技術[4]，本文以鋼架結構建筑物為例，采用GNSS技術獲取監測站的實時差分定位(RTK)數據，開展將安全監測數據作精準測量數據處理的探索。目前在去噪處理方面使用的方法主要有傅里葉變換、經驗模態分解、小波神經網絡[5]等。考慮到CEEMD適用于非平穩信號的分析及小波分析在信號去噪方面的優良性能，本文采用CEEMD分解和小波變換混合去噪，降低數據處理過程產生的誤差，提高信號還原精度。經仿真和實際驗證，該方法適用于鋼架監測數據的分析和處理，能夠很好地反映出信號特征，避免有效信號的損失。

1 混合去噪方法

1.1 CEEMD分解

Huang等[6]展示了一種嶄新的時頻分析手段——希爾伯特-黃變換(Hilbert-Huang transform，HHT)。該方法首先采用EMD(empirical mode decomposition)算法篩選非平穩信號，依據其信號特征自適應地分解成為一系列IMF分量及一個殘余量；然后再對各個IMF分量進行希爾伯特變換，其結果能真實反映信號能量在時間及各尺度上的分布規律。傳統的時頻分析技術需要一定先驗知識才能得到優良效果[7-8]，可能還會受限于信號的線性及平穩性；EMD無須預先設定任何基函數，在理論上可以應用于任何信號的分解，其分解基于信號本身極值點的分布。但間斷信號、脈沖干擾和噪聲等成分會造成信號的間歇，這勢必影響極值點的選取，由錯誤包絡求得的IMF分量就會存在模態混疊問題，使IMF失去具體的物理意義。

Wu等[9]依據白噪聲功率譜密度平均分布的特性提出一種噪聲輔助分析方法(EEMD)，其主要原理是在原始噪聲信號中人為添加白噪聲，為抵消白噪聲帶來的影響需要增加集合平均次數，這無疑增加了計算代價甚至可能帶來誤差。不僅如此，對白噪聲幅度的考量也至關重要，當數值不滿足要求時無法克服模態混疊。Yeh等[10]在2010年基于EEMD提出了互補集合經驗模態分解(complementary EEMD，CEEMD)，為減少EEMD殘留的白噪聲，取兩次原始信號作為一組分別添加互為相反數的輔助白噪聲，組與組之間相互獨立，顯著降低了集合平均次數，同時能減少分解迭代次數、提高計算效率，克服了EEMD分解完備性差、重構誤差大的缺陷。

CEEMD分解主要依賴于EMD分解，共分為3個步驟：

i=1,2,…,Lq=1,2

(1)

式中，ui(t)是第i次添加的白噪聲；ξ0是噪聲幅度，一般為0.1～0.2倍信號標準差。

(2)

式中，k為本征模函數的階數。

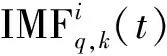
(3)

各階IMF分量集合平均后即為CEEMD分解的結果。

1.2 改進小波閾值去噪

小波變換作為當代流行的時頻分析方法，具備多尺度、去相關等性質[9]，特別是對隨機噪聲的抑制效果良好。小波變換涉及到基函數選取，以及閾值函數、閾值規則和分解層數的選擇。Dohono[10]于1995年提出閾值去噪方法，認為含噪信號在各尺度的分量其信噪能量是分離的，存在一個與小波系數w有關的臨界閾值λ，當w>λ時，認為此時信號占據主要部分，需要保留；當w≤λ時，認為此時噪聲為主體，應當將其舍棄，這便是硬閾值函數的由來。軟閾值不是僅對噪聲進行抑制，而是根據閾值的大小對小波系數進行向零逼近，最后對各個尺度下濾波信號進行重構，獲得降噪信號。小波閾值去噪基本步驟如下：

1)選取合理的分解層數和基函數，對原始含噪信號進行小波分析，獲取低頻系數和高頻細節分量。

2)對小波系數進行閾值處理，選擇合適的閾值規則，采用全局閾值或分層閾值的方式，經由小波閾值函數的濾波保留期望的小波分量。

3)利用小波逆變換重構各尺度分量，得到去噪信號。

硬閾值、軟閾值方法是常用的閾值處理手段。硬閾值的函數表達式為：

(4)

軟閾值函數的表達式為：

(5)

硬閾值在閾值點存在突變點，函數值不連續，導致信號產生振蕩，光滑度下降；而軟閾值雖然沒有間斷點，但是處理前后的小波系數會存在恒定偏差，這將影響到信號的重構相似度。為克服以上兩種方法的缺陷，在此提出新的閾值函數方法。

改進閾值函數的表達式為：

(6)

1.3 基于CEEMD的改進小波閾值去噪法

對于含噪的形變監測信號，當有用信號含量比較低時，若采用小波閾值去噪，極大可能會將隱匿于大量噪聲中的低幅值有用信號一并去除。如單純使用CEEMD分解去噪時，通常根據相關性法則，在剔除噪聲的過程中，含有最多噪聲成分的高頻IMF分量首先被剔除[8]，這樣會喪失高頻有效信息。本文提出的方法是力圖用CEEMD分解聯合小波閾值去噪來處理鋼架監測數據中的誤差，彌補單一方法處理形變監測數據時存在的不足，提高監測精度。用混合方法進行去噪處理主要步驟如下：

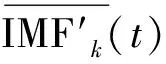
(7)

按照正常EMD分解重構的流程，會將各個IMF分量作自相關，與含噪信號的自相關曲線進行對比分析，根據經驗篩選處理后的IMF分量。由于隨機噪聲的自相關曲線是一個尖峰，而興趣信號具備一定寬度的自相關主瓣，IMF分量自相關的表現會依據所含信號和噪聲能量的比例逼近信號或噪聲。本文對全部IMF分量作小波閾值去噪，不用考慮IMF分量的選擇。

2 仿真實驗

為模擬長時間形變數據，采用MATLAB自帶的Blocks標準測試信號，調節因子N取16，在原始信號中添加信噪比為-5 dB的白噪聲還原真實的噪聲環境。原始信號和帶噪信號如圖2所示。

分別對帶噪的信號進行EMD、CEEMD分解，CEEMD每次疊加白噪聲的幅度ξ0選取為0.2倍的含噪信號標準差，循環疊加次數為100。由圖3可見，CEEMD分解能夠有效處理模態混疊問題，而其效果取決于噪聲幅度的選取。幅值過小的白噪聲無法抵消環境噪聲的影響，幅值過大的白噪聲會直接導致原始信號失真。本文在此未檢驗白噪聲幅值的影響。

為驗證混合算法的可行性，針對原始信號分別進行3組實驗，方案如下：1)直接進行軟閾值和硬閾值去噪，統一選擇極大極小規則進行分層閾值去噪，小波基函數為sym5，分解層數為5；2)對原始信號進行EMD和CEEMD分解重構，這里舍棄了IMF1至IMF4的分量，得到最優效果；3)在CEEMD分解的基礎上保留所有IMF成分，采用改進閾值函數對每一個IMF成分進行去噪，其中改進閾值函數中t選為0.2，再采用軟、硬閾值進行對比實驗，最終去噪效果見圖4。

這里采用信噪比SNR和均方根誤差RMSE衡量算法優劣：

(8)

(9)

式中，s(t)為原始信號，x′(t)為去噪信號。

圖4(a)和(b)反映了硬閾值和軟閾值的缺陷，硬閾值濾除噪聲的同時也濾除了低幅度的有效信號，軟閾值把各個小波系數按照閾值進行縮減。圖4(c)和(d)顯示，直接舍棄近似無關的IMF分量，帶來的誤差會更加明顯。圖4(e)和(f)將軟閾值和硬閾值混合到CEEMD分解中，相比單純使用軟閾值或硬閾值，信噪比得到提高。圖4(g)改進閾值能夠調節小波系數的衰減程度，克服了軟、硬閾值的弊端，雖然波形上存在一些毛刺，但從表1可知其性能優于其他兩種混合算法。

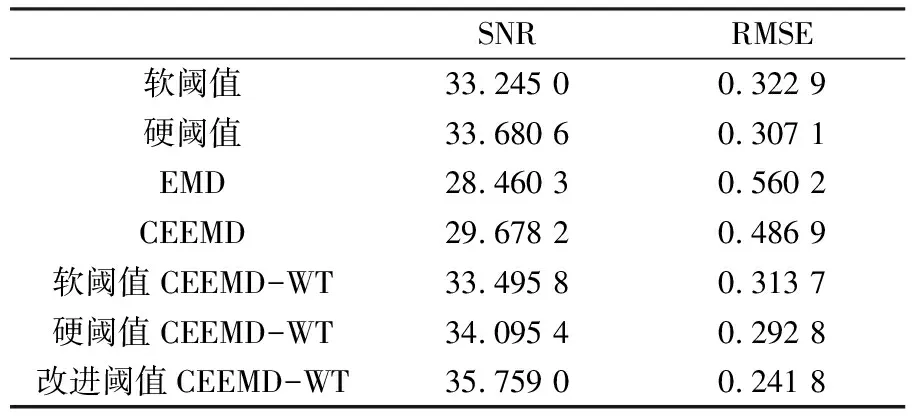
表1 Blocks信號去噪后的SNR、RMSE

3 實例驗證

為驗證混合算法在鋼架結構沉降數據處理中的可行性，于2020-10-26～27在杭州富陽市金鑫廣場進行桁架張拉測試。監測位置為圖5(a)紅色箭頭所指處，位于桁架中部略偏右，測試內容主要是監測施工輔助支架拆除過程中桁架下沉高度數據的變化情況。圖5(b)是金鑫廣場桁架總體結構及張拉部位示意圖，主要監測4個圓管柱上的斜拉索張拉過程中鋼結構的形變情況，及撐架卸載過程中桁架的下沉情況。

測試結果如圖6所示(數據監測頻率為2 Hz)，其中黑色部分：共9 772個數據，監測時間為2020-10-26 16:06～17:26，持續時間約1.3 h，為繩索張拉到50%張力過程；紅色部分：共23 808個數據，監測時間為2020-10-27 8:00～11:25，持續時間約3.3 h，為繩索張拉到80%張力過程；藍色部分：共13 610個數據，監測時間為2020-10-27 12:42～14:37，持續時間約1.9 h,為切割掉下面支撐架過程。

原始數據處理過程中，小波閾值去噪的基函數改為sym7、分解層數改為7。圖7是金鑫廣場桁架高程變化，通過改進閾值CEEMD-WT降噪后，顯著提高了信號分辨率。經表2實例再次驗證，混合算法降噪效果更為理想，較表現最好的硬閾值去噪方法均方根差下降0.7 mm。

表2 鋼架結構監測數據去噪后的SNR、RMSE

4 結 語

本文在固有的模態分解和小波閾值去噪的基礎上構建了互補集合經驗模態分解和改進小波閾值函數的混合去噪算法，首先對含噪信號作CEEMD分解，將各個IMF進行改進小波閾值的降噪，最后還原成降噪后的信號。其中，改進的小波閾值函數很好地緩解了軟閾值對恒定偏差的影響，也規避了硬閾值閾值點的間斷性。經過仿真及實例驗證，改進后的混合算法相比單一的模態分解或傳統小波閾值去噪方法精度至少提高0.7 mm，該算法可以有效處理形變監測中帶來的噪聲問題。