基于狀態(tài)空間建模的智能農(nóng)機(jī)模型辨識(shí)與柔化控制

袁洪良 郭 銳 薛夢(mèng)琦 盧瀟瀟 楊浚宇 徐立鴻

(1.同濟(jì)大學(xué)電子與信息工程學(xué)院， 上海 201804； 2.中移(成都)產(chǎn)業(yè)研究院， 成都 610041)

0 引言

我國(guó)各類農(nóng)業(yè)機(jī)械保有量大，研制智能農(nóng)機(jī)裝備是我國(guó)智慧農(nóng)業(yè)發(fā)展的重點(diǎn)任務(wù)。傳統(tǒng)農(nóng)業(yè)機(jī)械(農(nóng)機(jī))作業(yè)勞動(dòng)強(qiáng)度大，作業(yè)效率不高，作業(yè)質(zhì)量參差不齊。隨著導(dǎo)航技術(shù)和車輛控制技術(shù)的發(fā)展，傳統(tǒng)農(nóng)機(jī)裝備正在逐步向智能化精準(zhǔn)化發(fā)展。自動(dòng)導(dǎo)航控制算法具有比人類駕駛員的作業(yè)精度更高，降低農(nóng)機(jī)駕駛員的工作負(fù)擔(dān)，提高生產(chǎn)效率等優(yōu)勢(shì)[1-4]。

農(nóng)機(jī)自動(dòng)導(dǎo)航算法是農(nóng)機(jī)自動(dòng)導(dǎo)航系統(tǒng)的核心，主要有預(yù)瞄、追蹤、模糊、PID和基于模型的控制等類別[5-9]。

許多研究中使用了基于運(yùn)動(dòng)學(xué)模型的控制算法[10-15]。運(yùn)動(dòng)學(xué)模型的特點(diǎn)是建模簡(jiǎn)單、易于實(shí)現(xiàn)，但模型精度不高。在變速行駛、高速行駛和不平整地面工況中，往往無(wú)法滿足橫向控制的精確性和穩(wěn)定性要求，因此有研究提出了基于農(nóng)機(jī)動(dòng)力學(xué)模型的控制方法。文獻(xiàn)[15-17]建立了一種新型的農(nóng)機(jī)航向角速度動(dòng)力學(xué)模型，在此基礎(chǔ)上設(shè)計(jì)了LQR控制器，在農(nóng)機(jī)的高速行駛時(shí)具有較好的控制效果。EATON等[18-19]將反步(Backstepping)控制方法應(yīng)用到農(nóng)機(jī)的路徑跟蹤控制中，取得了較好的效果。RAJAMANI[20]指出隨著車輛速度的提高，車輛運(yùn)動(dòng)學(xué)模型不能準(zhǔn)確描述系統(tǒng)，動(dòng)力學(xué)模型具有更高的精度。

本文以東風(fēng)DF1004-2型拖拉機(jī)為實(shí)驗(yàn)平臺(tái)，使用實(shí)驗(yàn)法對(duì)其橫擺運(yùn)動(dòng)進(jìn)行狀態(tài)空間動(dòng)力學(xué)模型辨識(shí)，并通過(guò)仿真平臺(tái)和實(shí)驗(yàn)測(cè)試進(jìn)行模型驗(yàn)證。在此基礎(chǔ)上設(shè)計(jì)柔化LQR控制策略以期較好地解決農(nóng)機(jī)速度切變時(shí)的弱穩(wěn)定問(wèn)題。

1 農(nóng)機(jī)自動(dòng)導(dǎo)航系統(tǒng)設(shè)計(jì)與實(shí)現(xiàn)

農(nóng)機(jī)自動(dòng)導(dǎo)航系統(tǒng)包括農(nóng)機(jī)自動(dòng)導(dǎo)航控制終端、伺服電機(jī)、角度傳感器、北斗衛(wèi)星定位模塊、RTK基準(zhǔn)站、車載觸控平板計(jì)算機(jī)等。控制終端負(fù)責(zé)信息采集和控制計(jì)算；伺服電機(jī)是方向盤執(zhí)行機(jī)構(gòu)，用于轉(zhuǎn)動(dòng)方向盤；角度傳感器用于反饋導(dǎo)向輪角度；RTK基準(zhǔn)站提供北斗差分校正信息，北斗模塊提供農(nóng)機(jī)位置航向信息，RTK-北斗能夠?qū)崿F(xiàn)厘米級(jí)定位[21]；觸控平板計(jì)算機(jī)用于人機(jī)交互。

1.1 自動(dòng)導(dǎo)航硬件系統(tǒng)搭建

硬件部分設(shè)計(jì)主要包括自動(dòng)導(dǎo)航終端和RTK基站的印刷電路板，以及前輪轉(zhuǎn)角傳感器、方向盤電機(jī)和轉(zhuǎn)向管柱的適配機(jī)構(gòu)，系統(tǒng)架構(gòu)如圖1所示。

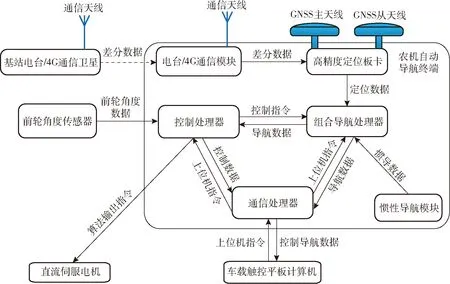
圖1 智能農(nóng)機(jī)系統(tǒng)架構(gòu)Fig.1 Intelligent agricultural machinery system architecture

上述硬件設(shè)計(jì)合適的結(jié)構(gòu)后安裝固定在農(nóng)機(jī)上，使用農(nóng)機(jī)自身12 V蓄電池供電，圖2為完成硬件搭建的東風(fēng)DF1004-2型拖拉機(jī)自動(dòng)導(dǎo)航實(shí)驗(yàn)平臺(tái)。

圖2 智能農(nóng)機(jī)自動(dòng)導(dǎo)航系統(tǒng)實(shí)驗(yàn)平臺(tái)Fig.2 Intelligent automatic driving system for agricultural tractor

1.2 農(nóng)機(jī)模型辨識(shí)

為提升控制性能，對(duì)農(nóng)機(jī)自動(dòng)導(dǎo)航系統(tǒng)進(jìn)行包括橫擺動(dòng)力學(xué)的狀態(tài)空間建模。在運(yùn)動(dòng)學(xué)模型中，橫向運(yùn)動(dòng)模型只有航向角一個(gè)狀態(tài)，這使得控制策略中也只能使用當(dāng)前的航向角作為反饋。如果橫向運(yùn)動(dòng)模型階數(shù)提高，即把航向角速度也作為一個(gè)狀態(tài)進(jìn)行建模，則控制器將具備根據(jù)航向角運(yùn)動(dòng)的趨勢(shì)進(jìn)行調(diào)節(jié)的能力，從而提升控制系統(tǒng)的快速性、穩(wěn)定性和精度。

基于上述思路，建立農(nóng)機(jī)運(yùn)動(dòng)四維狀態(tài)空間模型，4個(gè)狀態(tài)分別為農(nóng)機(jī)橫向誤差、航向角、航向角速度和前輪轉(zhuǎn)角，農(nóng)機(jī)路徑跟蹤示意圖如圖3所示。

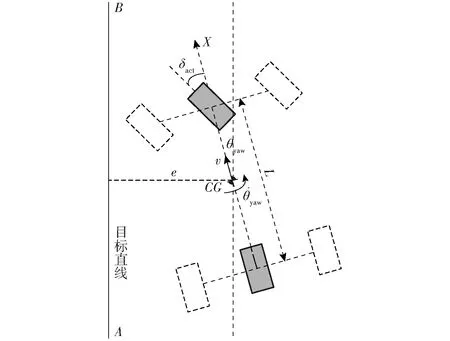
圖3 農(nóng)機(jī)路徑跟蹤示意圖Fig.3 Path following diagram of agricultural tractor

圖3中，e為農(nóng)機(jī)橫向誤差，θyaw為農(nóng)機(jī)航向角，δact為農(nóng)機(jī)實(shí)際前輪轉(zhuǎn)角，v為農(nóng)機(jī)縱向速度。由運(yùn)動(dòng)學(xué)幾何關(guān)系得到農(nóng)機(jī)橫向誤差e的變化率

(1)

在小角度條件下，式(1)可近似為

(2)

本文所選方向盤執(zhí)行機(jī)構(gòu)是直流伺服電機(jī)，通過(guò)雙環(huán)反饋控制設(shè)計(jì)為轉(zhuǎn)角伺服系統(tǒng)。控制量輸入到實(shí)際的前輪轉(zhuǎn)角的動(dòng)力學(xué)模型為一階模型，即

(3)

式中δcmd——農(nóng)機(jī)指令前輪轉(zhuǎn)角

K1——一階系統(tǒng)增益

τ——一階系統(tǒng)時(shí)間常數(shù)

s——拉普拉斯算子

根據(jù)車輛動(dòng)力學(xué)理論，在硬路面上輪胎抓地良好的條件下，航向角速度、車速和前輪轉(zhuǎn)角之間的關(guān)系式為

(4)

式中L——農(nóng)機(jī)軸距

在小角度條件下可以對(duì)tanδact進(jìn)行近似，得

(5)

考慮到農(nóng)田土壤松軟、農(nóng)機(jī)輪胎側(cè)滑等因素，輪胎側(cè)向力的建立不像硬路面那么快速，因此本文假設(shè)，航向角速度在式(5)的基礎(chǔ)上，還存在一個(gè)一階滯后環(huán)節(jié)。因此在s域，航向角速度和前輪轉(zhuǎn)角的關(guān)系可表示為

(6)

式中r——航向角速度

K2——一階滯后環(huán)節(jié)的比例系數(shù)

T——一階滯后環(huán)節(jié)的時(shí)間常數(shù)

式(6)反變換至?xí)r間域即可得農(nóng)機(jī)橫擺動(dòng)力學(xué)模型

(7)

又由于農(nóng)機(jī)航向角速度為航向角的導(dǎo)數(shù)，因此有

(8)

聯(lián)立式(2)～(8)可整理得農(nóng)機(jī)橫向動(dòng)力學(xué)狀態(tài)空間方程為

(9)

考慮到農(nóng)機(jī)循AB線穩(wěn)態(tài)行駛時(shí)導(dǎo)向輪調(diào)整幅度較小，因此在系統(tǒng)辨識(shí)實(shí)驗(yàn)設(shè)計(jì)中分別以±3°、±5°和±8°作為農(nóng)機(jī)前輪轉(zhuǎn)角的階躍輸入信號(hào)，每個(gè)指令轉(zhuǎn)角均在旱田中進(jìn)行了多組實(shí)驗(yàn)。通過(guò)Matlab系統(tǒng)辨識(shí)工具箱處理，結(jié)果顯示在不同指令前輪轉(zhuǎn)角作用下，各參數(shù)辨識(shí)結(jié)果較為一致，實(shí)驗(yàn)結(jié)果如表1所示。該結(jié)果也驗(yàn)證了式(6)中一階滯后環(huán)節(jié)的假設(shè)具有可行性。

對(duì)表1中各組數(shù)據(jù)作均值處理可得農(nóng)機(jī)的各項(xiàng)參數(shù)最終值，K1為1.01、τ為0.32、K2為-1.16、T為0.06。

為驗(yàn)證農(nóng)機(jī)橫向動(dòng)力學(xué)模型參數(shù)的準(zhǔn)確性，在Simulink中搭建農(nóng)機(jī)狀態(tài)空間模型進(jìn)行模型驗(yàn)證，如圖4所示。

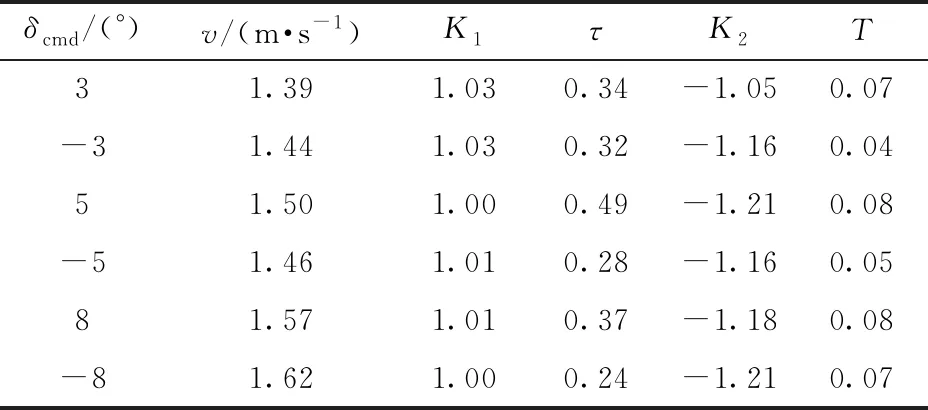
表1 農(nóng)機(jī)系統(tǒng)辨識(shí)實(shí)驗(yàn)結(jié)果Tab.1 Experimental result of agricultural tractor system identification

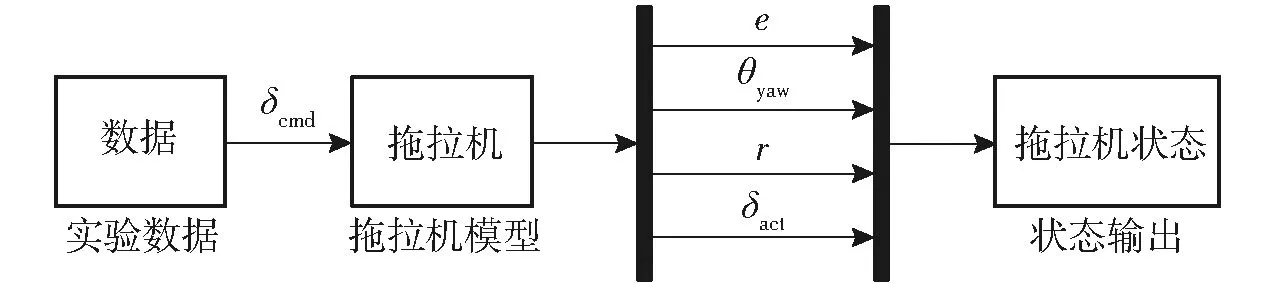
圖4 拖拉機(jī)橫向動(dòng)力學(xué)模型驗(yàn)證平臺(tái)Fig.4 Verification platform for lateral dynamic model of agricultural tractor

仿真實(shí)驗(yàn)中選取指令前輪轉(zhuǎn)角為5°，行駛速度為1.5 m/s的工況，得到農(nóng)機(jī)指令前輪角-實(shí)際前輪轉(zhuǎn)角模型驗(yàn)證效果如圖5所示，農(nóng)機(jī)實(shí)際前輪轉(zhuǎn)角-航向角模型驗(yàn)證效果如圖6所示。

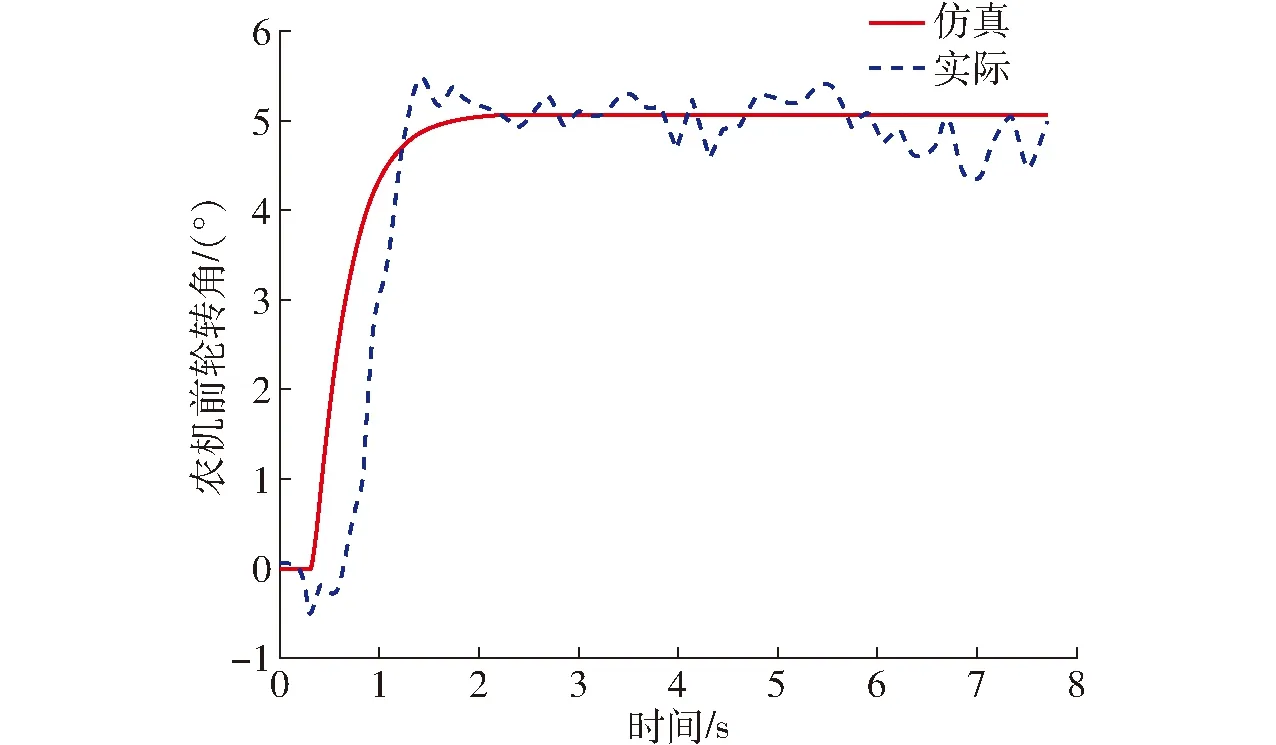
圖5 農(nóng)機(jī)前輪轉(zhuǎn)角模型驗(yàn)證Fig.5 Verification of front wheel angle model of agricultural tractor

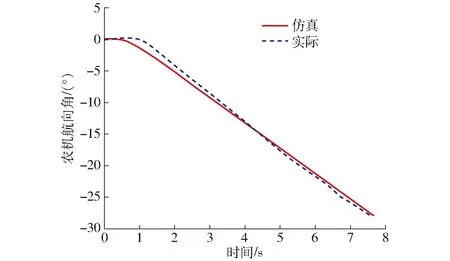
圖6 農(nóng)機(jī)航向角模型驗(yàn)證Fig.6 Verification of yaw angle model of agricultural tractor

從圖5、6中可以看出，相同輸入下，農(nóng)機(jī)實(shí)際航向角和仿真航向角的曲線吻合程度較高，且穩(wěn)態(tài)值驗(yàn)算也符合式(7)，表明辨識(shí)結(jié)果準(zhǔn)確，所建模型可以支持狀態(tài)空間反饋控制。

1.3 農(nóng)機(jī)自動(dòng)導(dǎo)航控制算法

(1)將所建立和驗(yàn)證的動(dòng)力學(xué)模型作為控制對(duì)象進(jìn)行狀態(tài)空間反饋設(shè)計(jì)。把式(9)改寫為狀態(tài)空間標(biāo)準(zhǔn)表達(dá)式

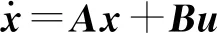
(10)

其中

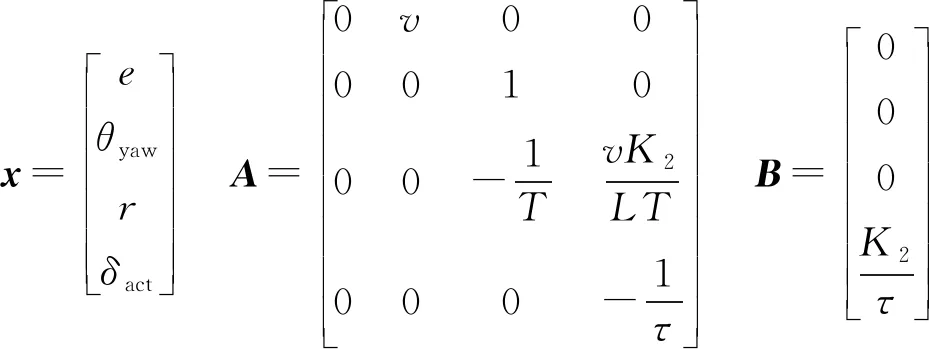
式中x——系統(tǒng)狀態(tài)A——系統(tǒng)矩陣

B——輸入矩陣u——系統(tǒng)輸入

(2)設(shè)計(jì)LQR控制器對(duì)農(nóng)機(jī)前輪轉(zhuǎn)角進(jìn)行控制。LQR控制器是以系統(tǒng)狀態(tài)變量x和控制變量u的線性二次型為性能指標(biāo)，使閉環(huán)系統(tǒng)漸近穩(wěn)定且指標(biāo)最優(yōu)的控制器。該問(wèn)題在線性定常系統(tǒng)上有系統(tǒng)性的解法且控制效果良好，因此在工業(yè)上有廣泛應(yīng)用。假設(shè)農(nóng)機(jī)自動(dòng)導(dǎo)航控制系統(tǒng)的性能指標(biāo)為J，則

(11)

式中Q——狀態(tài)變量加權(quán)矩陣

R——系統(tǒng)輸入加權(quán)矩陣

Q為半正定常數(shù)對(duì)稱矩陣，R為正定常數(shù)對(duì)稱矩陣。實(shí)際調(diào)參過(guò)程中，選擇Q為對(duì)角陣，又由于Q和R不需要同時(shí)變化，且系統(tǒng)是單輸入系統(tǒng)，因此可選取R=1。本文經(jīng)過(guò)實(shí)驗(yàn)調(diào)試，Q取值為

Q=diag[0.3 0.5 0.001 0.000 1]

最優(yōu)控制器是使性能指標(biāo)式(11)達(dá)到最小的狀態(tài)反饋控制器，其形式是

u=-Kx

(12)

求解最優(yōu)控制問(wèn)題就是要尋找增益矩陣K，使得上述性能指標(biāo)J最小，根據(jù)龐特里亞金極小值原理和李雅普諾夫穩(wěn)定性理論可以推導(dǎo)出，當(dāng)

K=R-1BTP

(13)

Q+ATP+PA-PBR-1BTP=0

(14)

成立時(shí)性能指標(biāo)J達(dá)到最小值[22]。

式(13)、(14)中P為對(duì)稱正定矩陣，式(14)也稱作代數(shù)黎卡提方程。代數(shù)黎卡提方程可以轉(zhuǎn)換為一個(gè)多元二次方程組進(jìn)行解析求解，但由于算法需要在嵌入式控制器上使用C語(yǔ)言進(jìn)行實(shí)現(xiàn)，且系統(tǒng)矩陣A中存在變量v，解析法求解代碼較為復(fù)雜，故本文中采用迭代法來(lái)求解P，算法為

Φ0=0

E=(I-A)-1(I-A)

G=2(I-A)-1B

H=R+BT(I-A)-1Q(I-A)-1B

W=Q(I-A)-1B

while |Φi+1-Φi|≥εdo

T=(ETΦiG+W)(GTΦiG+H)-1(ETΦiG+W)

Φi+1=ETΦiE-T+Q

算法中ε為可調(diào)節(jié)正常數(shù)，I為單位陣，矩陣E、G、H、W、T、Φ為中間變量。算法迭代到滿足條件的Φi+1后(一般迭代30次即可收斂，計(jì)算時(shí)間不到10 ms)，可以求得黎卡提方程的解為

P=2(I-AT)-1Φi+1(I-A)-1

(15)

把迭代法求解結(jié)果式(15)與Matlab中解析法求解的結(jié)果進(jìn)行比對(duì)，驗(yàn)證了2種算法結(jié)果是一致的。

(3)設(shè)計(jì)柔化控制器。LQR控制器在無(wú)速度突變時(shí)的直線路徑跟蹤中性能較好，但是在農(nóng)機(jī)行駛速度發(fā)生突變時(shí)，算法輸出的控制指令有時(shí)會(huì)產(chǎn)生較大的振蕩，控制性能下降。因此在LQR控制器的基礎(chǔ)上，進(jìn)一步設(shè)計(jì)了柔化控制器，其表達(dá)式為

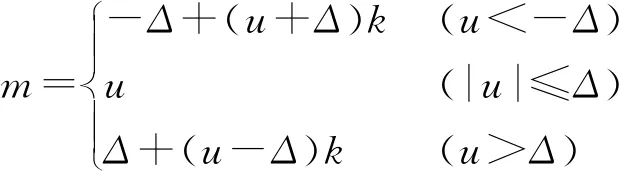
(16)

式中u——控制輸入m——控制輸出

Δ、k——柔化參數(shù)

系統(tǒng)整體控制架構(gòu)為雙閉環(huán)反饋控制，如圖7所示。內(nèi)環(huán)為方向盤電機(jī)的角度伺服控制，電機(jī)配置為轉(zhuǎn)速輸入模式，由PID控制器根據(jù)指令和實(shí)際轉(zhuǎn)角的誤差進(jìn)行調(diào)節(jié)。外環(huán)是基于狀態(tài)空間模型的LQR柔化控制器，實(shí)現(xiàn)農(nóng)機(jī)的路徑跟蹤控制。

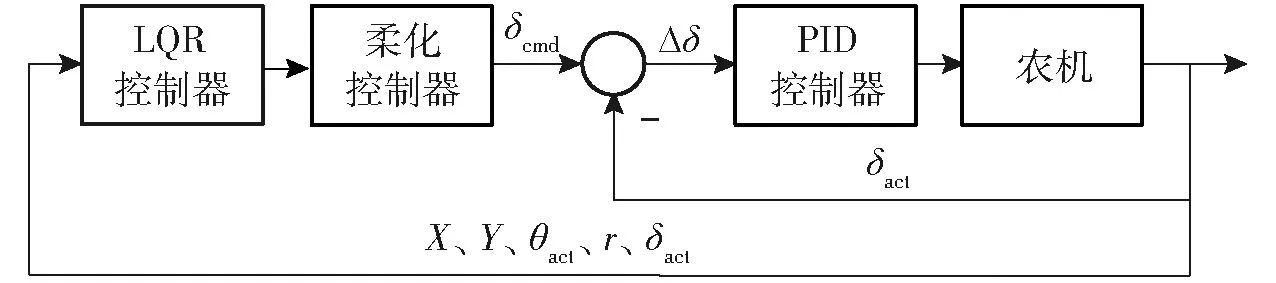
圖7 農(nóng)機(jī)雙閉環(huán)反饋控制框圖Fig.7 Block diagram of agricultural tractor control system

2 實(shí)驗(yàn)與結(jié)果分析

為驗(yàn)證上述控制方法的性能，在搭建的農(nóng)機(jī)自動(dòng)導(dǎo)航平臺(tái)上實(shí)現(xiàn)了LQR和柔化控制算法，并在實(shí)驗(yàn)田中針對(duì)未柔化勻速場(chǎng)景、未柔化速度突變場(chǎng)景和柔化速度突變場(chǎng)景分別進(jìn)行了實(shí)驗(yàn)，測(cè)試現(xiàn)場(chǎng)如圖8所示。

圖8 農(nóng)機(jī)測(cè)試現(xiàn)場(chǎng)Fig.8 Dongfeng agricultural tractor test scenario

2.1 未柔化、無(wú)速度突變場(chǎng)景

本項(xiàng)實(shí)驗(yàn)考察了單獨(dú)使用LQR控制器時(shí)，在常見的勻速直線路徑跟蹤作業(yè)中的性能。圖9、10顯示了在勻速條件下農(nóng)機(jī)橫向誤差、航向角、車輛行駛速度和前輪轉(zhuǎn)角變化曲線。可以看到控制系統(tǒng)經(jīng)過(guò)5 s左右的調(diào)節(jié)之后，農(nóng)機(jī)進(jìn)入穩(wěn)態(tài)行駛階段，穩(wěn)態(tài)誤差波動(dòng)范圍在0.03 m以內(nèi)。圖10也顯示在整個(gè)行駛過(guò)程中農(nóng)機(jī)前輪實(shí)際轉(zhuǎn)角能夠較好地跟蹤控制指令，電機(jī)的角度伺服性能良好。可見，單獨(dú)LQR控制器對(duì)無(wú)速度突變的直線路徑跟蹤性能較好。

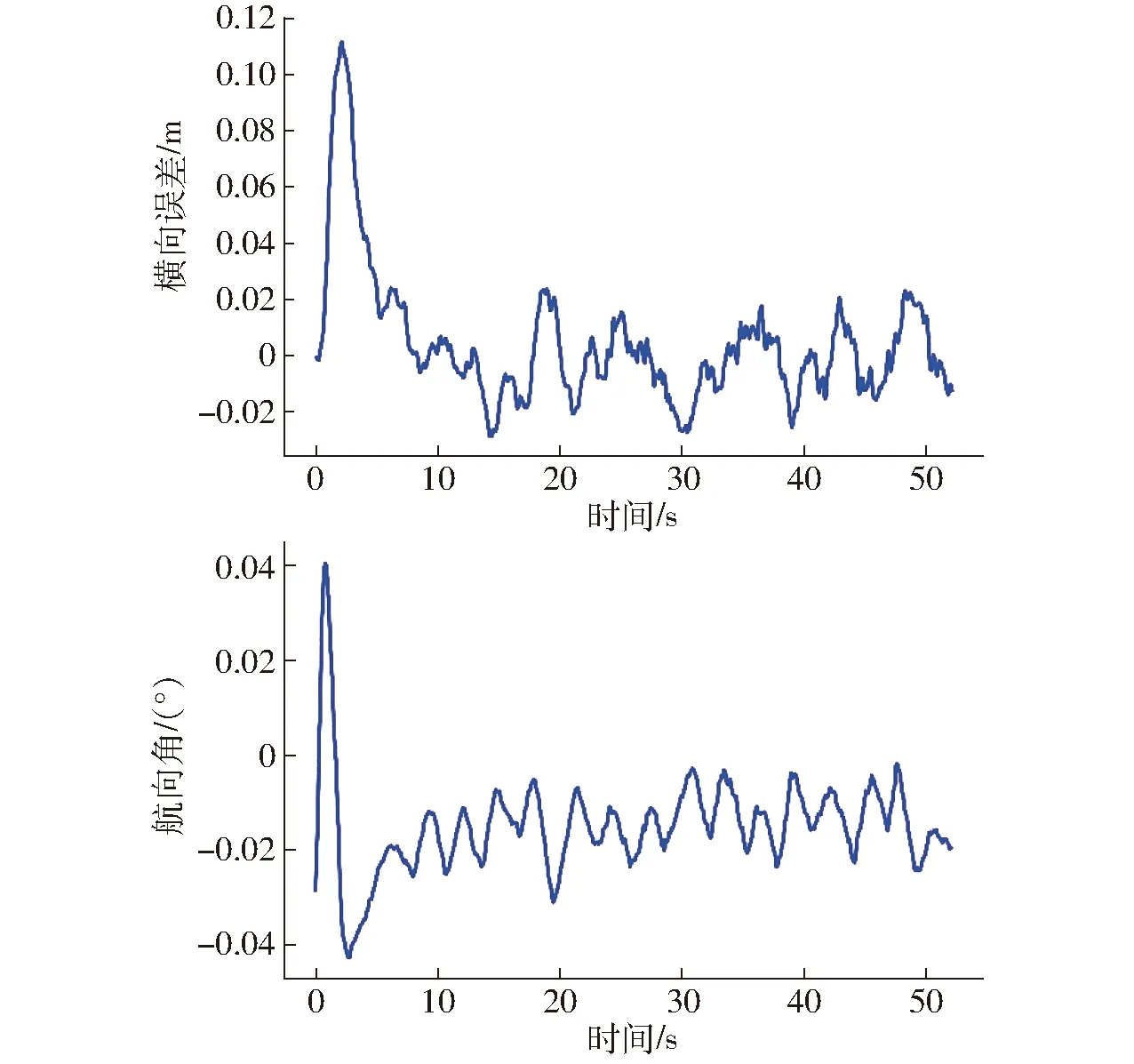
圖9 未柔化、無(wú)速度突變時(shí)橫向誤差和航向角Fig.9 Lateral error and yaw angle of agricultural tractor before flexible control without speed change

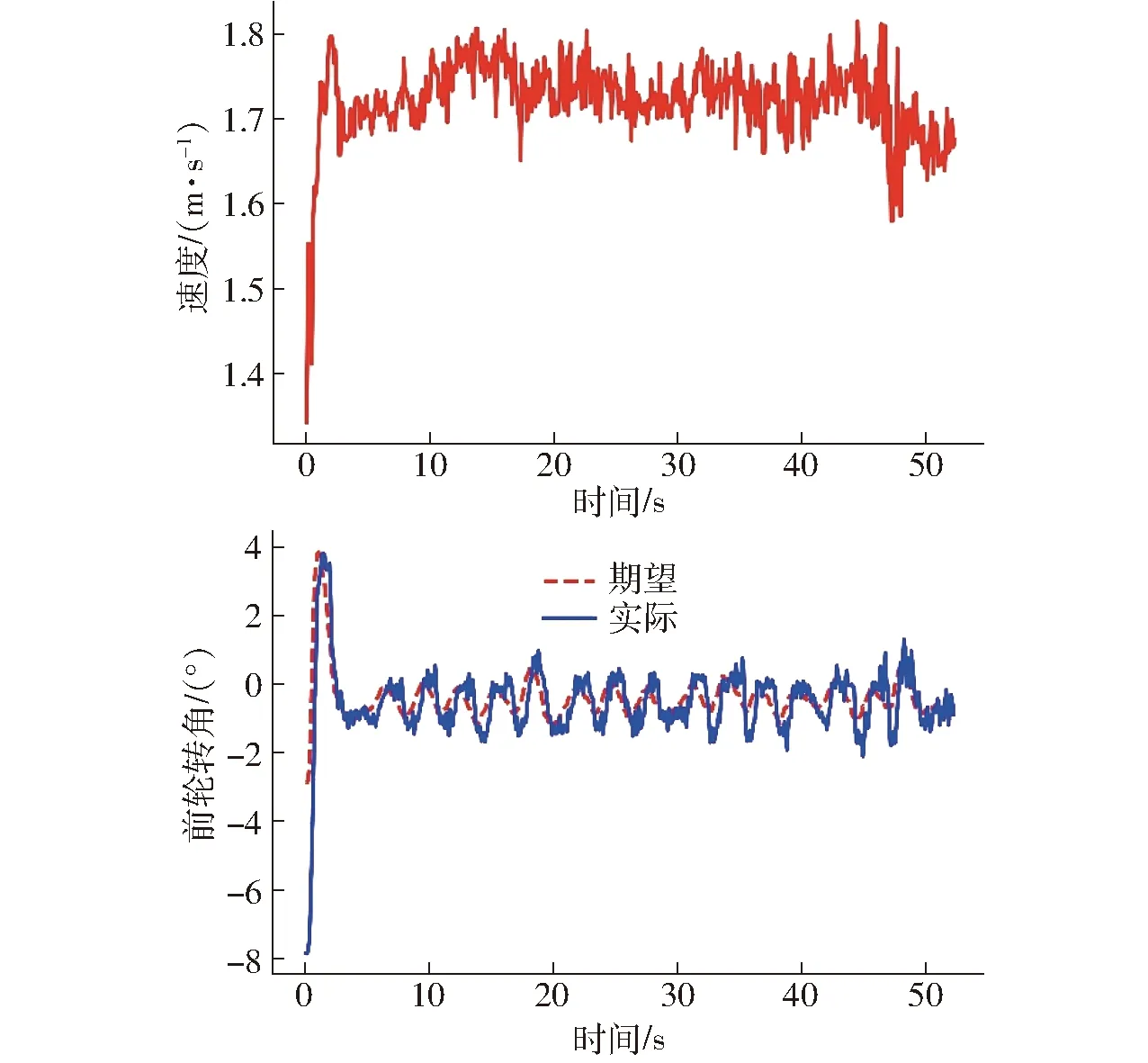
圖10 未柔化、無(wú)速度突變時(shí)農(nóng)機(jī)速度和前輪轉(zhuǎn)角Fig.10 Speed and front wheel angle of agricultural tractor before flexible control without speed change

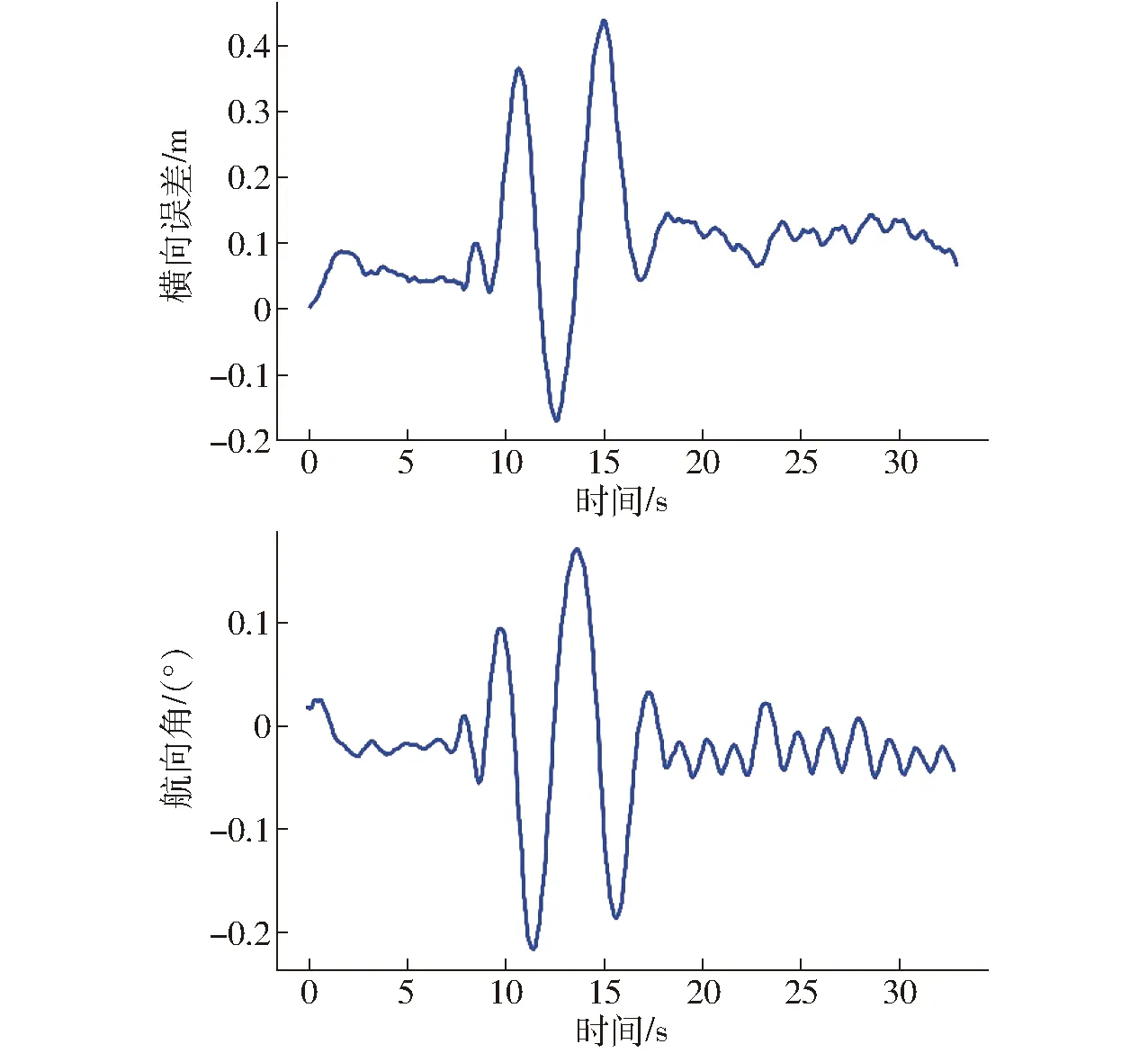
圖11 未柔化、速度突變時(shí)農(nóng)機(jī)橫向誤差和航向角Fig.11 Lateral error and yaw angle of agricultural tractor before flexible control with speed change

2.2 未柔化、有速度突變場(chǎng)景

本實(shí)驗(yàn)考察了單獨(dú)LQR控制器在速度突變條件下的響應(yīng)。圖11、12為農(nóng)機(jī)從勻速突然變速再到勻速工況下的橫向誤差、航向角、速度和前輪轉(zhuǎn)角的變化曲線。從圖中可以看到，LQR控制器對(duì)速度變化表現(xiàn)較為敏感，控制輸出和系統(tǒng)狀態(tài)均產(chǎn)生較大幅度的振蕩，穩(wěn)定性下降。系統(tǒng)經(jīng)過(guò)約10 s調(diào)整以后，仍能再次趨于穩(wěn)定，但動(dòng)態(tài)過(guò)程中位置誤差最大值達(dá)到了0.4 m以上，農(nóng)機(jī)車身出現(xiàn)明顯的擺動(dòng)，不滿足實(shí)際作業(yè)需求。因此，需對(duì)速度突變條件下的系統(tǒng)控制進(jìn)行柔化處理。

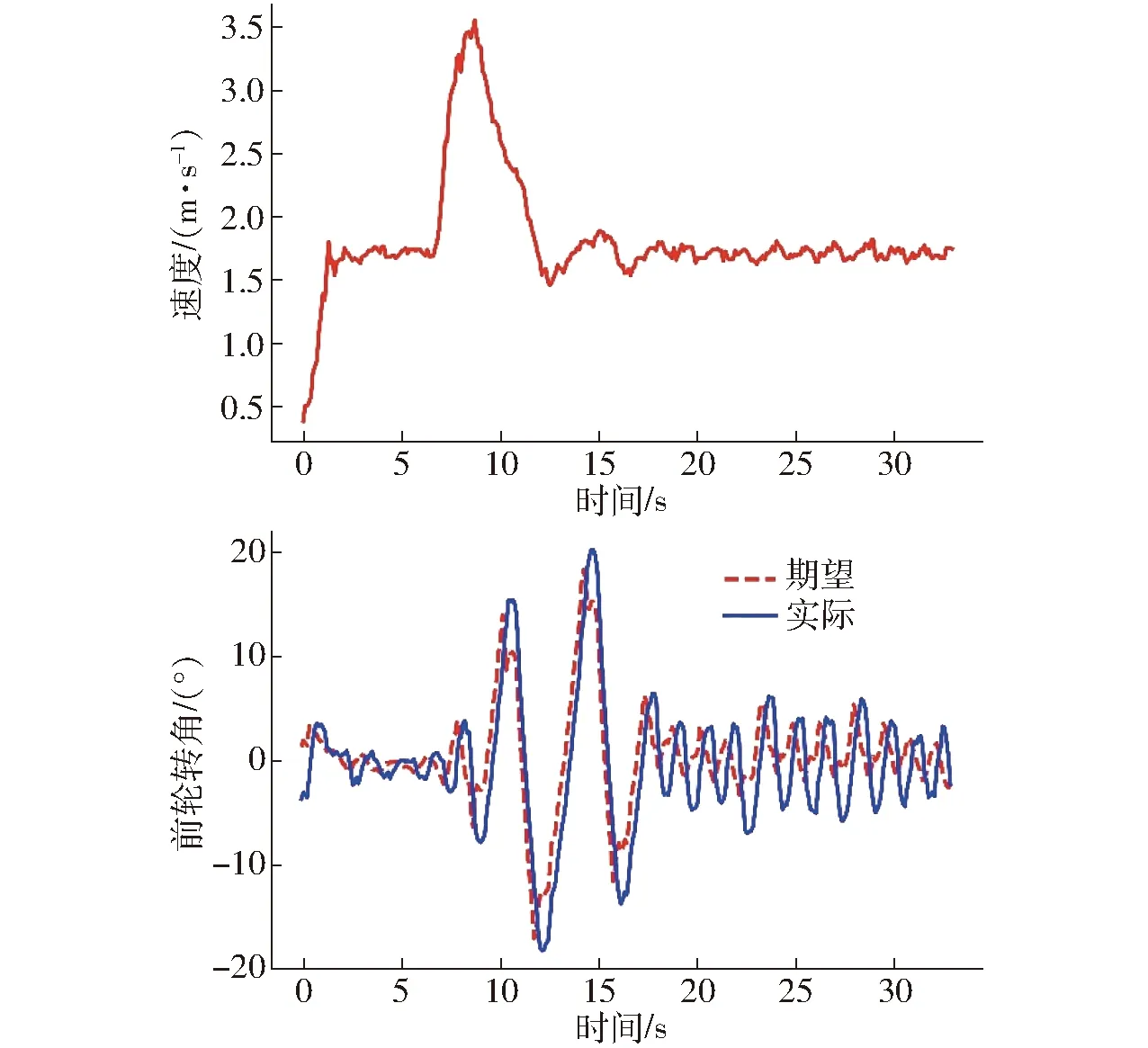
圖12 未柔化、速度突變時(shí)農(nóng)機(jī)速度和前輪轉(zhuǎn)角Fig.12 Speed and front wheel angle of agricultural tractor before flexible control with speed change

2.3 柔化、有速度突變場(chǎng)景

實(shí)驗(yàn)中在LQR控制器后串聯(lián)了柔化控制器，增加了系統(tǒng)的阻尼，使速度突變?cè)斐傻臓顟B(tài)變化有一個(gè)較平緩的過(guò)渡過(guò)程，以解決速度突變條件下發(fā)生的穩(wěn)定性弱化的問(wèn)題。本場(chǎng)景中速度進(jìn)行了連續(xù)階梯狀突變，比圖12中的速度變化更為劇烈，未柔化控制器在本場(chǎng)景中會(huì)迅速發(fā)散、失控。柔化控制后的效果如圖13、14所示。

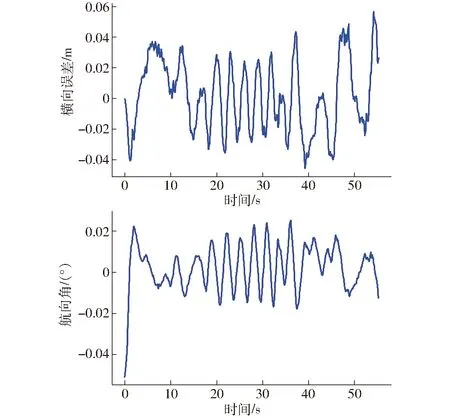
圖13 柔化控制后農(nóng)機(jī)橫向誤差和航向角Fig.13 Lateral error and yaw angle of agricultural tractor after flexible control

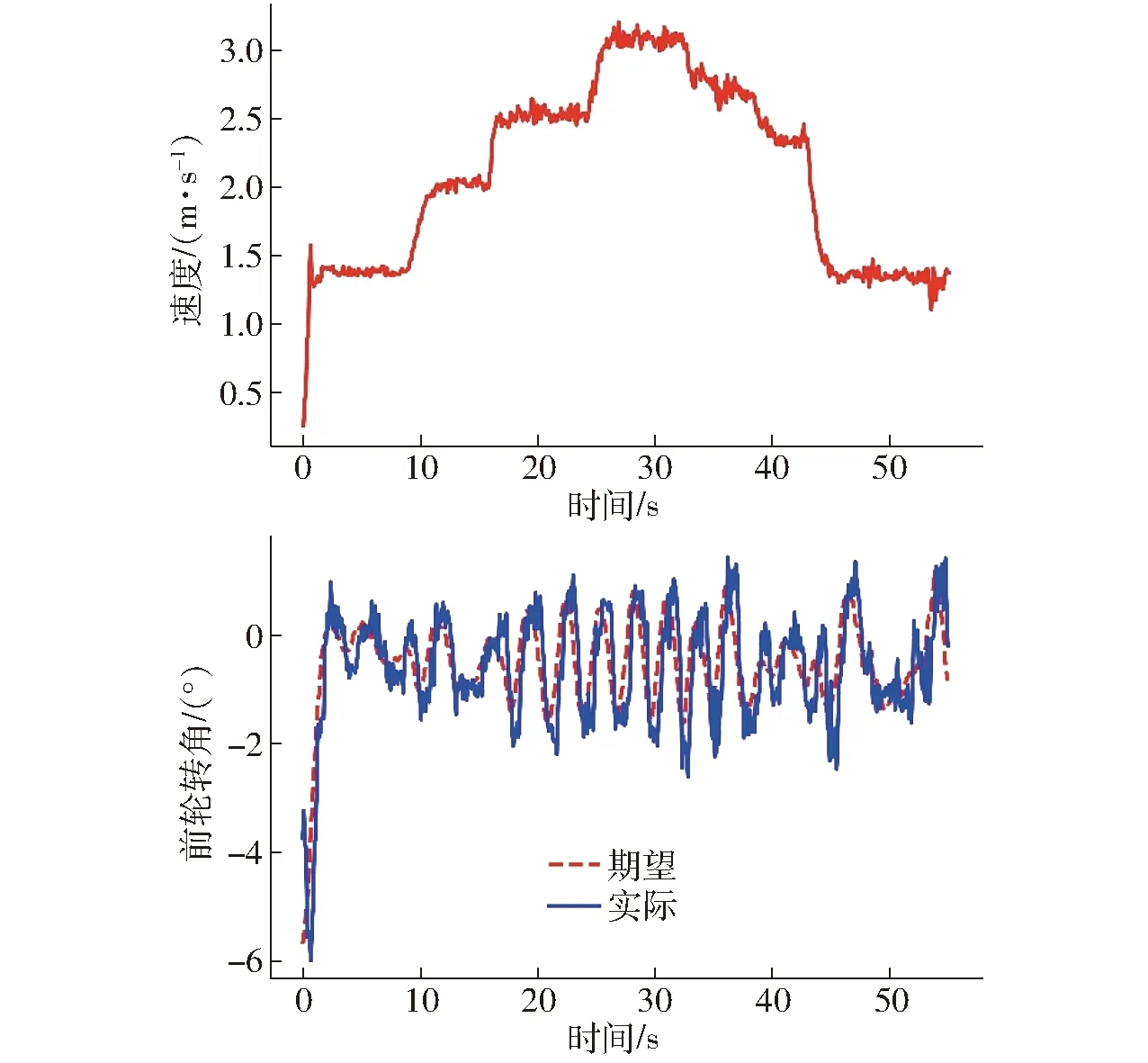
圖14 柔化控制后農(nóng)機(jī)速度和前輪轉(zhuǎn)角Fig.14 Speed and front wheel angle of agricultural tractor after flexible control

由圖13、14可知，在連續(xù)變速的條件下，進(jìn)行柔化控制優(yōu)化之后，農(nóng)機(jī)仍保持穩(wěn)定，雖然農(nóng)機(jī)速度的變化會(huì)導(dǎo)致農(nóng)機(jī)被控狀態(tài)產(chǎn)生小幅波動(dòng)，比無(wú)速度突變場(chǎng)景(圖9、10)略微增大，但是由于對(duì)算法輸出進(jìn)行了柔化控制，前輪轉(zhuǎn)角并未產(chǎn)生大幅振蕩，農(nóng)機(jī)橫向誤差也始終維持在0.05 m以內(nèi)，農(nóng)機(jī)車身未產(chǎn)生擺動(dòng)。

總體而言，柔化控制改善了農(nóng)機(jī)在變速條件下的穩(wěn)定性，無(wú)論是勻速情況還是變速情況，農(nóng)機(jī)均保持穩(wěn)定，并且有較短的調(diào)節(jié)時(shí)間以及較高的控制精度，滿足日常作業(yè)需求。

3 結(jié)束語(yǔ)

研究了農(nóng)機(jī)自動(dòng)導(dǎo)航中建模和控制的相關(guān)問(wèn)題。首先，搭建了農(nóng)機(jī)自動(dòng)導(dǎo)航的硬件系統(tǒng)。其次，對(duì)搭建的硬件平臺(tái)進(jìn)行動(dòng)力學(xué)建模，采用實(shí)驗(yàn)法分別建立了實(shí)際前輪轉(zhuǎn)角-航向角模型和期望前輪轉(zhuǎn)角-實(shí)際前輪轉(zhuǎn)角模型，并建立起包括農(nóng)機(jī)橫擺動(dòng)力學(xué)的狀態(tài)空間模型。選取橫向偏差、航向角、航向角速度和前輪轉(zhuǎn)角4個(gè)狀態(tài)，與基于運(yùn)動(dòng)學(xué)模型的控制系統(tǒng)不同，由于使用了航向角速度反饋，使得控制器能夠預(yù)見航向角的變化趨勢(shì)，并更快做出響應(yīng)。此外為了優(yōu)化在農(nóng)機(jī)速度切變時(shí)穩(wěn)定性減弱的問(wèn)題，對(duì)LQR算法的結(jié)果進(jìn)行了柔化處理，避免了導(dǎo)向輪和系統(tǒng)狀態(tài)的大幅振蕩，使農(nóng)機(jī)橫向誤差精度在勻速狀態(tài)下達(dá)到0.03 m，變速狀態(tài)下可維持在0.05 m以內(nèi)，農(nóng)機(jī)路徑跟蹤性能有明顯提升，可以滿足農(nóng)機(jī)日常作業(yè)需求。