基于神經網絡的軌道電路行車信號判斷＊

賈智奧，禹建麗，劉澤源，陳洪根

（1.鄭州航空工業管理學院管理工程學院，河南鄭州 450046；2.河南科技大學材料科學與工程學院，河南洛陽 471000）

1 研究背景

隨著“交通強國，鐵路先行”的國家戰略政策的實施，高鐵已經成為人們出行必不可少的交通工具，鐵路業也得到了突飛猛進的發展。近年來，隨著鐵路總里程數的增加，列車運行頻次不斷提高，鐵路運行的安全性逐漸成為鐵路運輸的主題。在保證安全性的前提下，現代鐵路還要提高鐵路運輸的效率，這就需要加大鐵路設備的建設從而達到效率和安全的雙重保障。而在各種鐵路設備中，軌道電路系統是列車控制系統的核心，是信號系統的重要組成部分。軌道電路設備故障引起鐵路信號系統故障的情況是鐵路事故的重要原因之一[1]。因此，軌道電路行車信號判斷的研究具有重要意義。

關于軌道電路方面的研究，國內學者已經取得了很多研究成果，曹雲夢等[2]采用BP 神經網絡對高壓脈沖軌道電路進行故障預測，實現了有關故障的識別分類，較傳統預測方法更為可行高效；彭麗宇等[3]采用神經網絡方法對鐵路軌道不平順進行預測分析，為鐵路軌道養護維修提供技術支持；陶漢卿等[4]將多分支BP神經網絡用于軌道電路故障預測，提高了預測準確率和計算效率；徐紹俊[5]以25 Hz 相敏軌道電路為研究對象，提出一種BP 神經網絡與模擬退火相結合的故障診斷方法，有效提高了診斷效率和準確度；米根鎖等[6]采用BP 神經網絡對軌道電路的分路不良進行故障預警，得到可靠預警結果等。而ZPW-2000R 型無絕緣移頻軌道電路是鐵路區間段的基礎設備，它根據主接入電壓、調接入電壓等數據來判斷是否有列車占用車道[7]，來達到自動控制目的，以提高運輸效率。

鑒于目前關于軌道電路行車信號判斷的研究相對較少，本文提出一種基于神經網絡的智能方法。通過采集軌道電路設備的列車運行實時數據，以軌道電路室內設備的主接收器調接入電壓為輸入，列車行車信號為輸出，構建人工神經網絡來判斷軌道電路行車信號，通過調節各層神經元的權值達到機器學習的效果。測試實驗研究表明，本文所提方法對軌道電路行車信號判斷準確率達到100%，體現了人工智能方法的高效性和可行性。

2 神經網絡模型

2.1 神經網絡拓撲結構及學習算法

由于受到生物神經元結構的信息傳遞的啟發[8]，W.McCulloch 和W.Pitts 提出了第一個神經網絡模型，開啟了人工神經網絡發展的時代。人工神經網絡具有自適應性、自學習性、自組織性、容錯性，并且具有并行式處理能力、分布式存儲能力、自動提取信息能力等[9]，其最主要的功能是非線性映射功能和較強泛化能力[10]。

BP 神經網絡（Back Propagation Neural Network）是人工神經網絡算法之一，是一種有效的分類和識別工具。BP 神經網絡學習過程分為信息正向傳播和誤差反向傳播過程。通過不斷調整各層神經元的權值使實際輸出與期望輸出之間的誤差不斷減小[11]，直到滿足精度要求。本文研究的BP 神經網絡模型如圖1 所示。

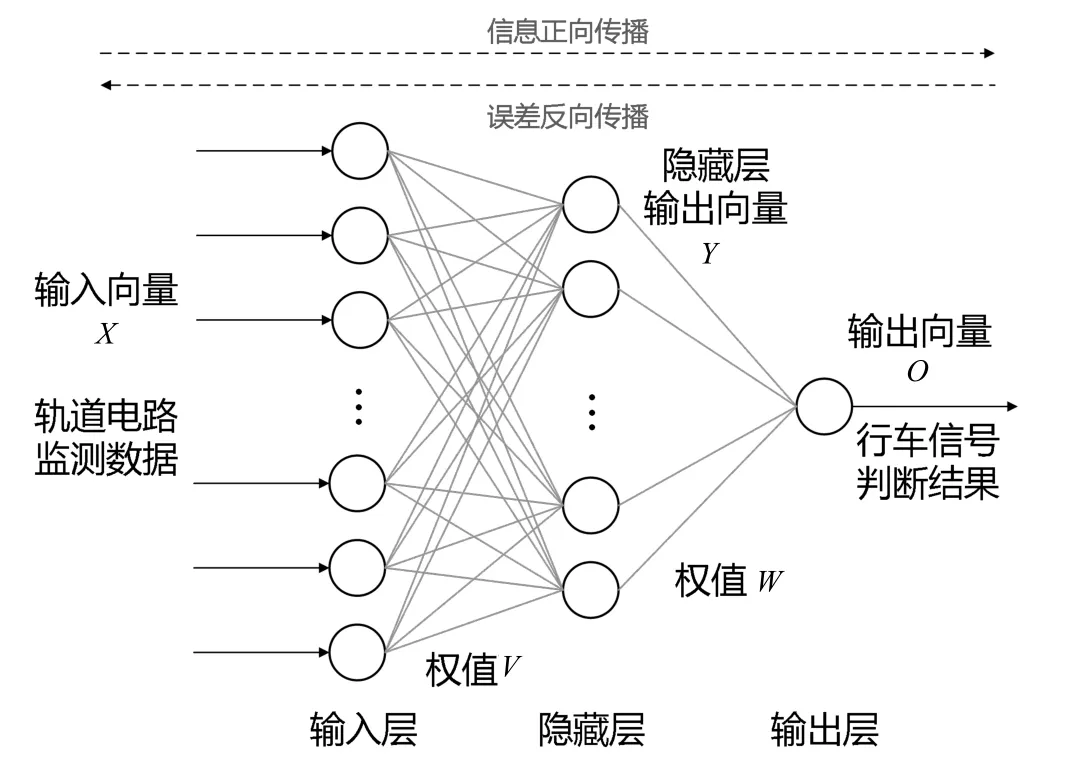
圖1 神經網絡結構

其中，網絡的輸入向量為X=（x1，x2，…，xi，…，xn）T，隱藏層輸出向量為Y=（y1，y2，…，yj，…，ym）T，輸出層輸出向量為O=（o1，o2，…，ok，…，xl）T，期望輸出向量為d=（d1，d2，…，dk，…，dl）T，輸入層到隱藏層的權值矩陣：V=（v1，v2，…，vj，…，vm），隱藏層到輸出層的權值矩陣：W=（w1，w2，…，wk，…，wl）。

對于輸出層，有：

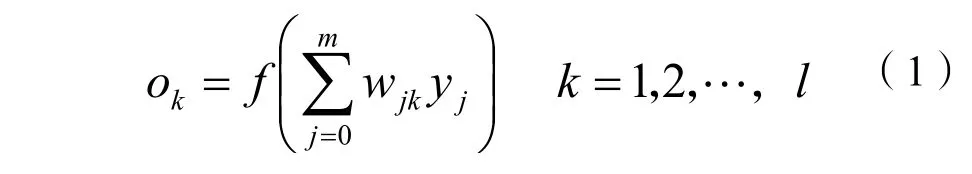
對于隱藏層，有：

公式（3）即期望輸出與輸出向量的誤差，又稱性能指標函數。

至此為網絡的信息正向傳播過程。若誤差E不滿足期望精度，則通過梯度下降法調整各層權值矩陣V和W，通過對誤差E求偏導數，可得到輸出層到隱藏層和隱藏層到輸出層的權值調整分別為：

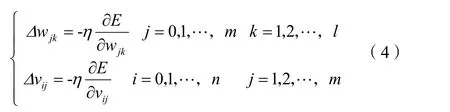
式（4）中，負號表示梯度下降；常數η∈（0，1），表示學習速率。

一般BP 神經網絡需要經過多次的信息正向傳播和誤差反向傳播不斷減小誤差[12]，可通過設置目標誤差精度和最大迭代次數來使網絡學習過程停止，最后通過保存相應的權值閾值即得到最終的模型。

盡管BP 神經網絡的非線性映射能力和泛化能力很強，可有效解決很多實際問題，但采用負梯度下降調整權值可能會陷入局部最小值，故引入動量因子來修正權值，使網絡學習速率加快且保持穩定。加入動量因子的權值調整為：

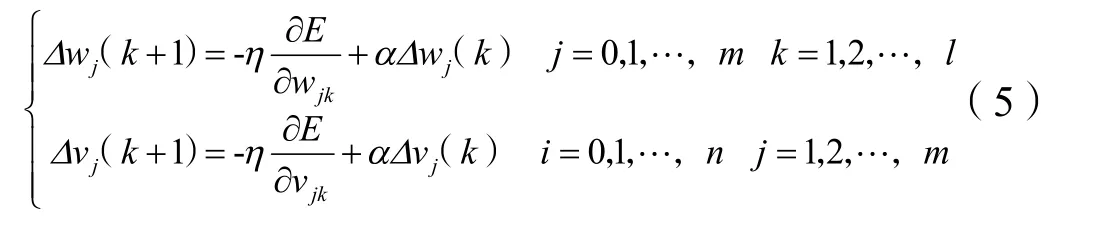
2.2 BP 神經網絡模型構建

本文實驗根據ZPW-2000R 型無絕緣移頻軌道電路系統設備采集的實時電壓數據來判斷行車信號，且主接收器的調接入電壓大小在軌道過車占用和正常空閑狀態有較為明顯的差別。實驗采集的軌道過車占用和正常空閑的調接入電壓數據變化如圖2 和圖3所示。

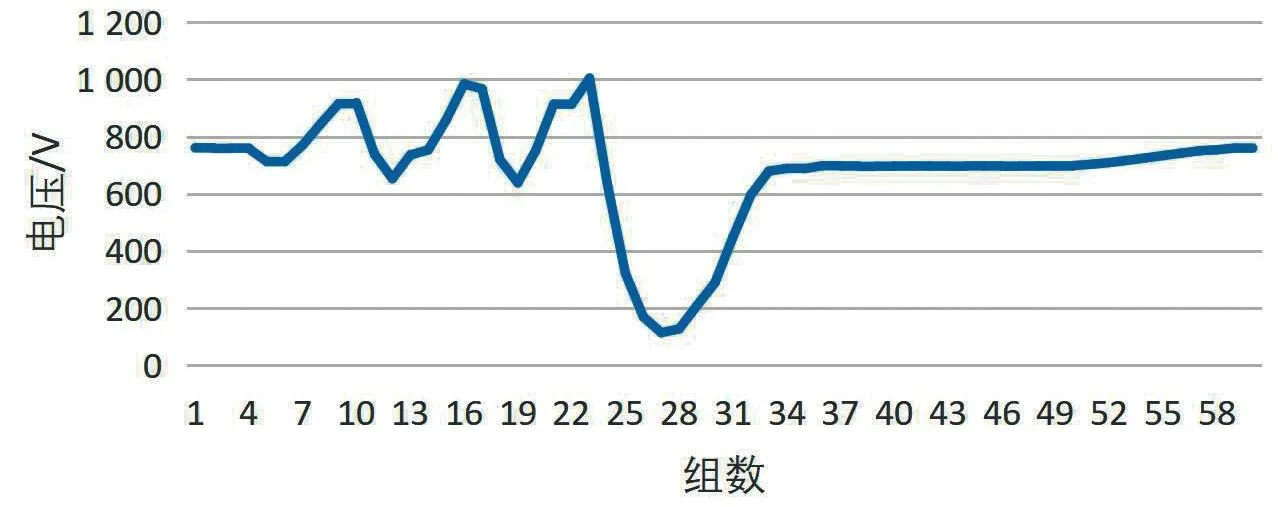
圖2 軌道行車占用電壓變化

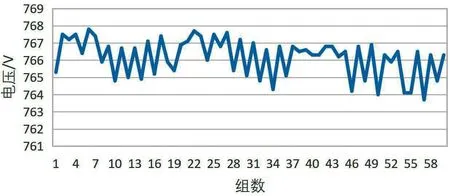
圖3 軌道正常空閑電壓變化

神經網絡模型構建的基礎是網絡的輸入和輸出，本文將軌道電路系統主接收器的調接入電壓實時數據作為網絡的輸入向量，由于監測目的是判斷是否有列車占用車道，所以將軌道電路行車信號判斷結果（過車占用或正常空閑）作為神經網絡輸出。

通過采集得到了15 組軌道過車的實時電壓數據，每組均為一個列向量，由于行車道每次過車的時間長短不一，導致了每組數據的維度不盡相同，所以取其中維度最高的60 維作為標準，將其余的數據前后補上車道正常電壓數據至所有數據均達到相同的維數60，得到了最終的60×15 車道過車占用數據組成的矩陣，對于車道的正常空閑數據采集了36 組，把15 組車道過車數據其中的11 組和36 組正常數據其中的20 組合并為一個60×31 的矩陣，即為最終的神經網絡訓練輸入矩陣P；其余的4 組過車數據和16 組正常數據合并為了60×20 的網絡行車信號判斷實驗的測試矩陣P2；對于網絡輸出，定義“車道過車占用”為1、“車道正常空閑”為0，得到MATLAB 中神經網絡訓練輸出矩陣T=[ones（1，11） zeros（1，20）]，同理可得網絡行車判斷實驗的輸出矩陣T2=[ones（1，4）zeros（1，16）]。

以下是神經網絡模型的一些基本參數的確定和選取。

輸入層和輸出層神經元個數：由于神經網絡輸入矩陣P、輸出矩陣T的維度分別為60 和1，確定輸入層和輸出層神經元個數分別為60 和1。

激活函數：本文網絡模型選取transig 函數為隱藏層激活函數，purelin 線性傳遞函數為輸出層激活函數，訓練函數為traingdx。運用信號正向傳播、誤差反向傳播的方式不斷調整各層之間的權值，減小誤差，提高準確率。

損失函數：模型的損失函數表征出了所有樣本與實際值的誤差總和。本文的回檢實驗采用默認的均方誤差（MSE）為性能函數，而行車判斷實驗采用平均絕對誤差（MAD）和均方誤差（MSE）來作為性能函數，其計算公式為：

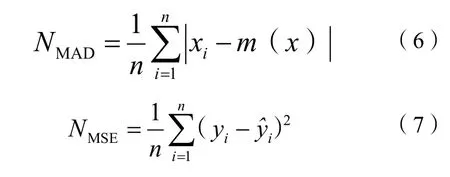
3 神經網絡訓練

采用MATLAB R2018b 軟件，先將輸入矩陣P進行歸一化處理，建立神經網絡模型，并進行回檢，得到初始回檢結果如圖4 所示。

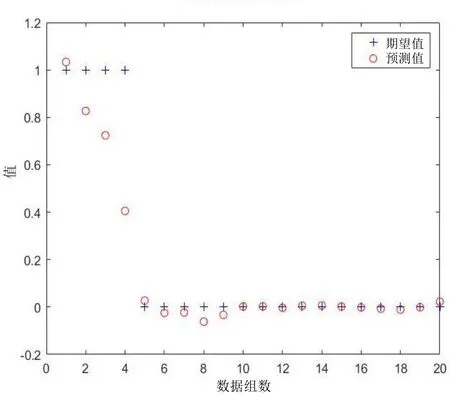
圖4 初步回檢結果

從圖4 可以看出，后3 組車道過車數據和前5 組車道正常數據的判斷結果較差，因此，后續實驗將所有對應數據打亂順序，之后再輸入到神經網絡中進行算法學習。

而隱藏層神經元個數依據經驗公式：

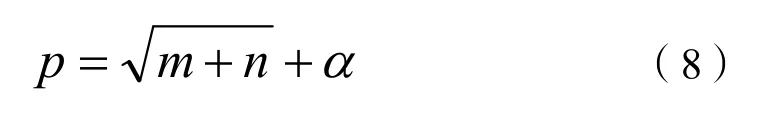
式（8）中：p、m和n分別為隱藏層、輸入層和輸出層神經元個數；α為1～10 的常數。

由上述公式（8）可以得出隱藏層神經元個數應介于9～18。

該行為中國工商銀行安徽省分行，在安徽省內，其綜合實力排名靠前，所以此結果證明了該模糊綜合評判模型的有效性和可行性。

通過神經網絡算法訓練、回檢及行車判斷實驗，發現當隱藏層神經元個數不同時模型回檢的均方差均在10-5量級，差別較小，所以采用行車判斷結果的平均絕對誤差和均方差來確定隱藏層神經元個數。并由公式（6）（7）計算出隱藏層神經元個數為9、10、11、12、13、14、15、16、17、18 的平均絕對誤差分別為0.369 00、0.366 76、0.293 63、0.315 26、0.401 32、0.375 35、0.388 71、0.418 65、0.357 28、0.382 78，均方誤差分別為0.298 91、0.293 73、0.195 44、0.221 63、0.342 88、0.320 35、0.335 56、0.366 99、0.307 85、0.339 02。

行車判斷結果誤差與隱藏層神經元個數的關系如圖5 所示。由圖可知，2 種誤差變化較為穩定，p為11 時均達到最小值為0.293 63 和0.195 44。

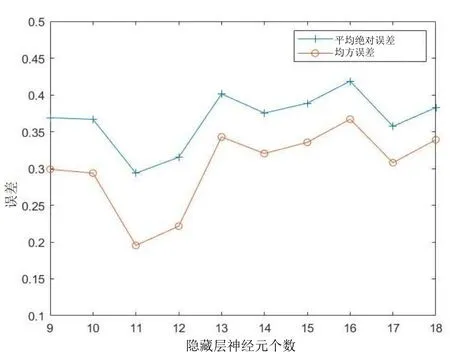
圖5 隱藏層神經元個數與誤差關系

當p=11 時，網絡訓練的均方差隨迭代次數的變化如圖6 所示，由圖可知，算法進行到第400 代時，均方差逐漸趨于穩定，當進行到1 000 代時，算法停止，即達到最大迭代次數的停止條件，且網絡均方差在第986 代達到1.27×10-5。

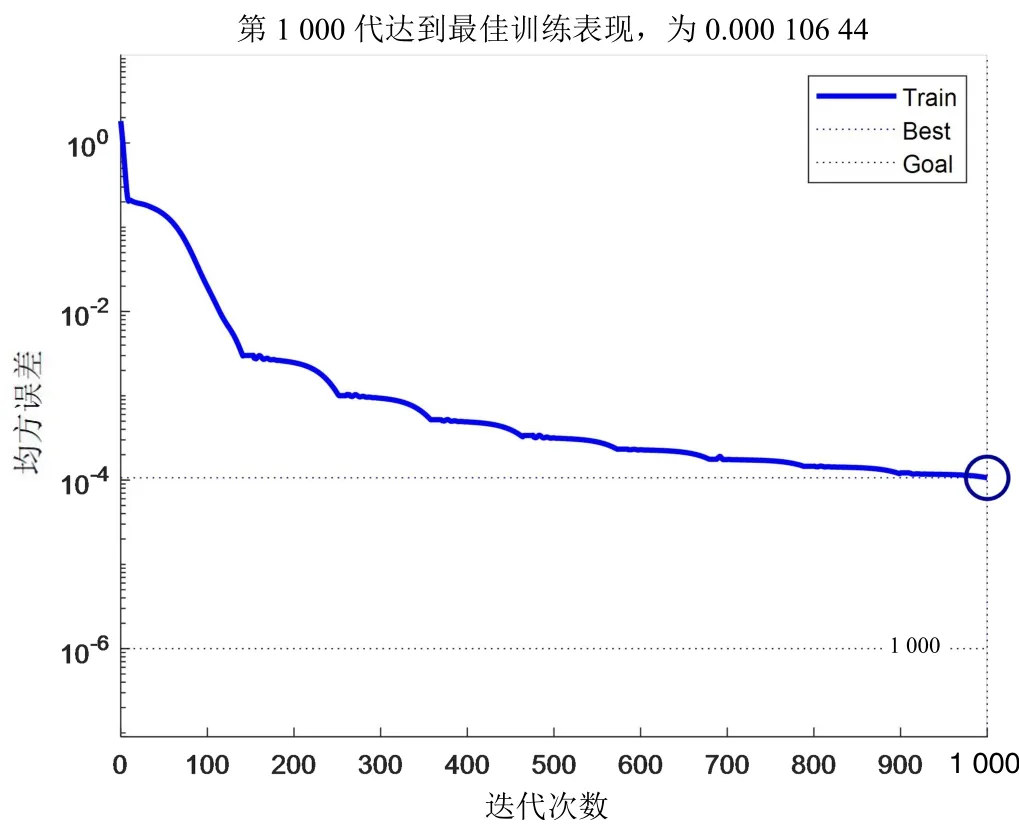
圖6 網絡均方差變化圖

此外，算法的迭代次數、學習率、目標精度等參數也會對判斷結果產生一定的影響。

對于學習率的選取，太低的學習率會減緩網絡的訓練速度，過高的學習率又會對損失函數產生影響，分別對學習率為0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.10 進行實驗，通過比較行車判斷結果的誤差來確定學習率，結果如圖7 所示。

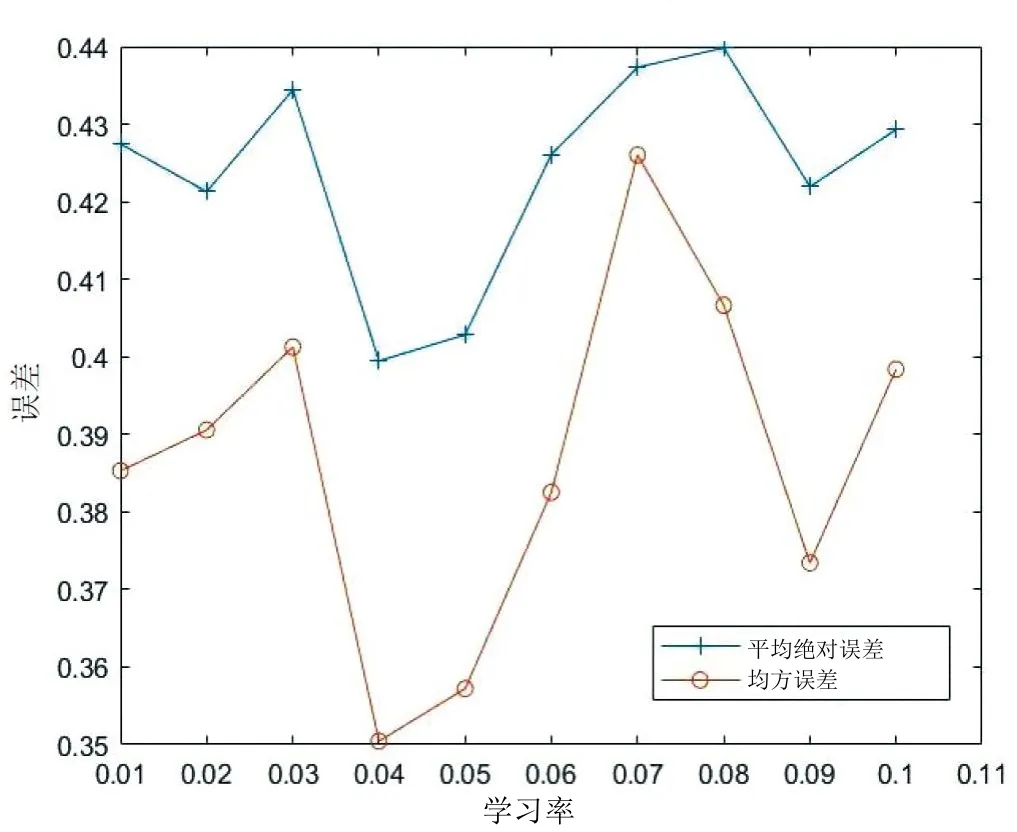
圖7 學習率與誤差關系

從圖7 可以看出，當學習率為0.04 時，兩種判斷誤差均達到最小，所以算法的學習率設置為0.04。

在反向傳播過程中動量因子的引入，既可加快學習速度又可保持算法穩定，具體表達式為：

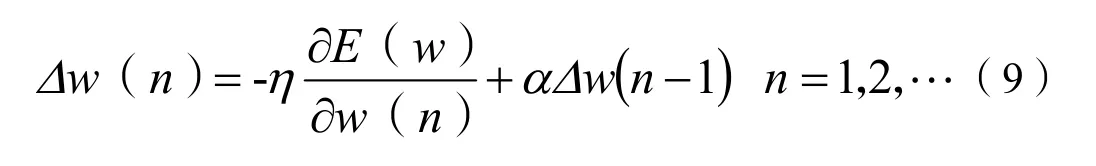
公式（9）中第二項為動量項，α∈（0，1），為動量因子。分別對0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9 進行訓練，得到動量因子和判斷結果誤差的關系如圖8 所示，從圖中可以看出，動量因子為0.1 時兩種誤差均達到最小，所以算法的動量因子設置為0.1。

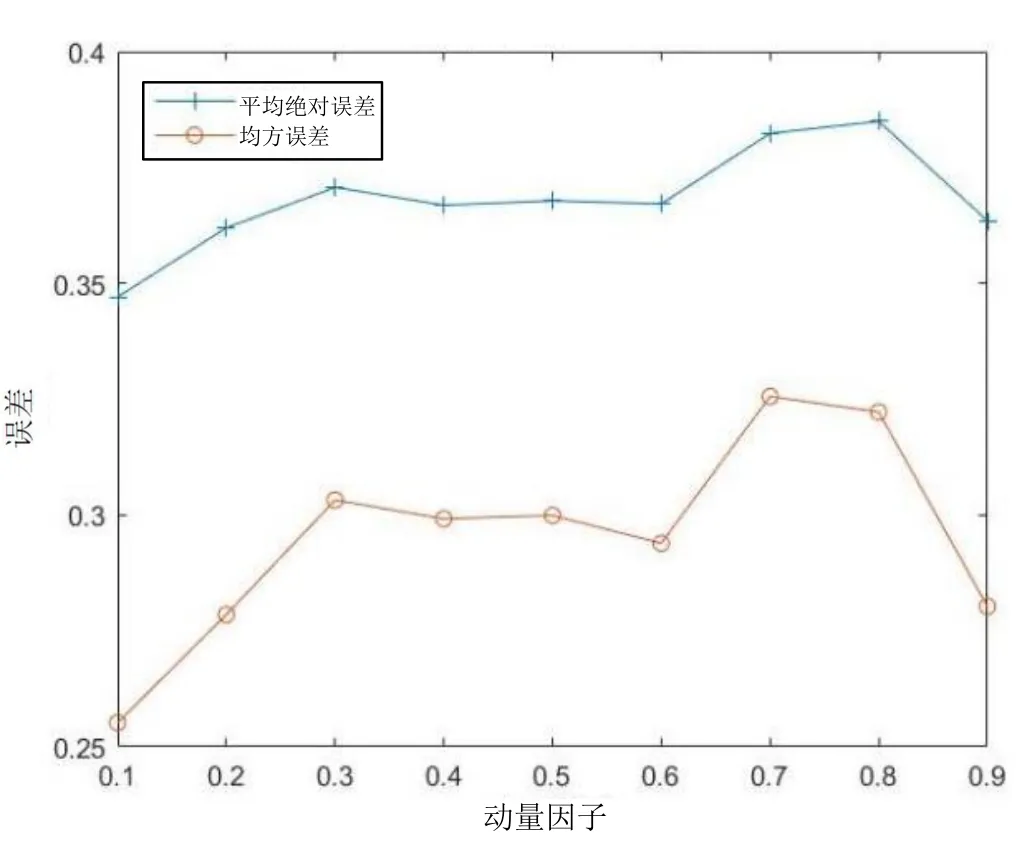
圖8 動量因子與誤差關系

本文確定的算法的相關參數如表1 所示。

表1 神經網絡模型參數

4 BP 神經網絡回檢實驗及行車判斷

采用p=11 的神經網絡判斷模型進行回檢實驗，將31 組行車信號實時數據（其中包括11 組過車占用數據和20 組正常空閑數據）輸入神經網絡，回檢結果如圖9 所示。

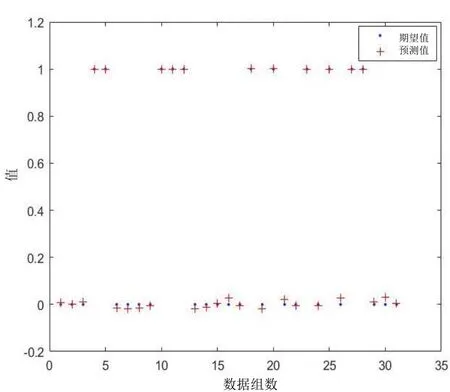
圖9 模型回檢結果

由圖9 可知，31 組回檢實驗數據的其中第4、5、10、11、12、18、20、23、25、27、28 組結果接近1，為過車占用信號。其余20 組的結果接近0，為正常空閑信號，回檢準確率為100%。

當神經網絡回檢完成后，為了驗證神經網絡對行車判斷的準確性，再把20 組的實時測試數據集P2（其中包括4 組過車占用數據和16 組正常空閑數據）代入訓練完成的神經網絡，進行軌道電路行車信號判斷實驗驗證。

對于模型的預測值，若大于等于0.5，記為1，表示為過車占用信號，小于0.5，記為0，表示為正常空閑信號，來檢驗結果是否為有效判斷。具體判斷結果如表2 所示。

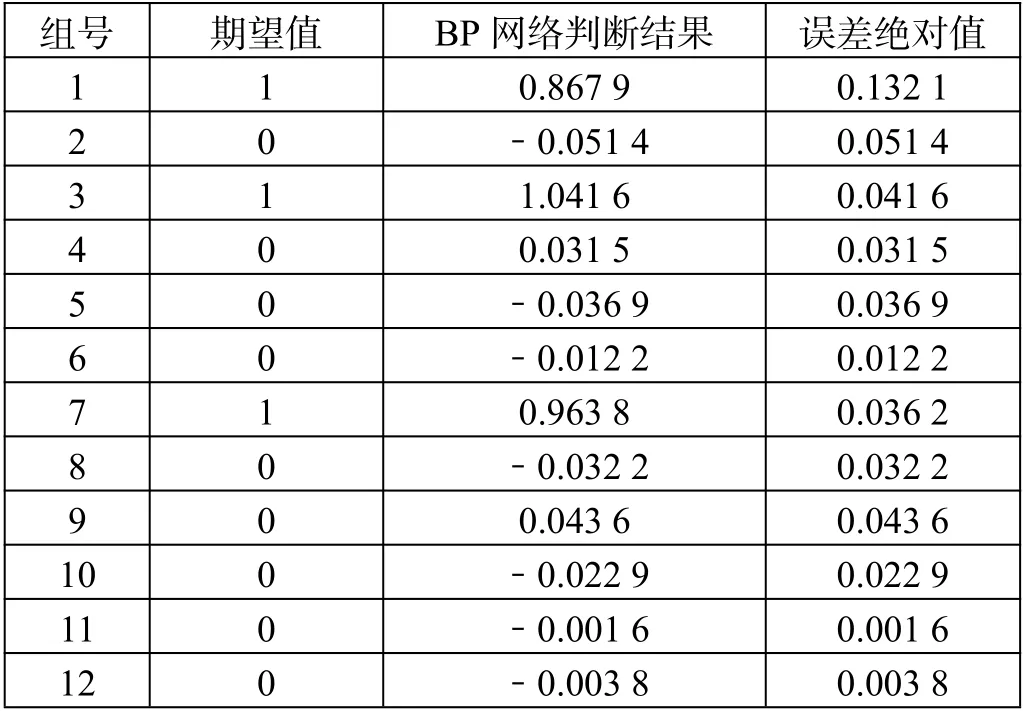
表2 模型測試結果

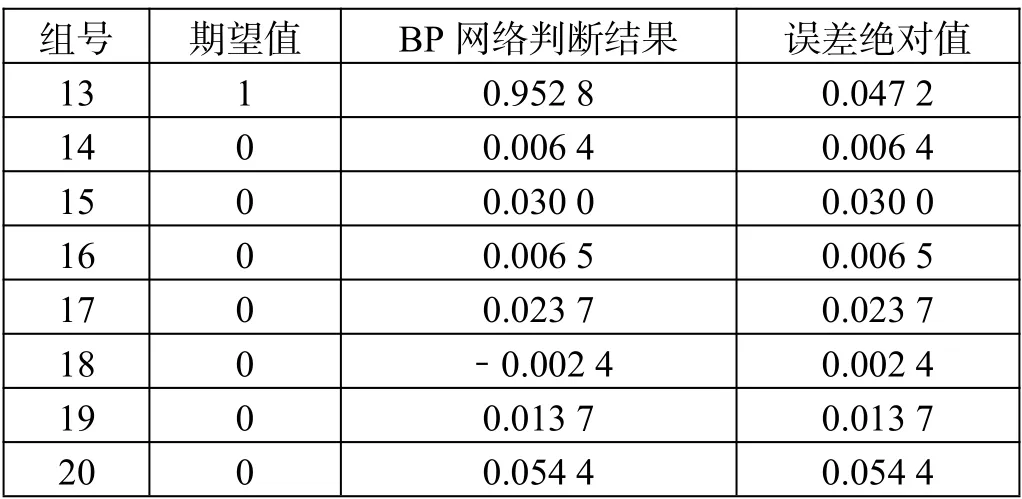
表2（續）

由表2 可知，20 組測試數據判斷結果中第1、3、7、13 測試組的結果均大于0.5，記為1，即過車占用信號，其余16 組小于0.5，記為0，即正常空閑信號，判斷準確率為100%。

5 基于RBF 神經網絡的行車判斷

徑向基函數（RBF）神經網絡是一種三層結構的前饋型人工神經網絡，包括輸入層、隱藏層和輸出層。從輸入層到隱藏層的是非線性變換，隱藏層的輸出層是線性變換[14]。

RBF 神經網絡需要求解的參數有基函數的中心、方差和隱藏層到輸出層的權值。一般采用自組織選取學習中心方法，即第一步通過無監督學習過程求解隱藏層的基函數中心和方差，第二步通過有監督學習過程求解隱藏層到輸出層的權值[15]。

RBF 神經網絡的隱藏層節點采用輸入模式與中心向量的距離（如歐式距離）作為函數的自變量，并使用徑向基函數作為激活函數。神經元的輸入離徑向基函數中心越遠，神經元的激活程度就越低。RBF 網絡的輸出與部分調參數有關，譬如，一個隱藏層輸出值只影響一個輸出層的輸出值，因此具有“局部映射”特性。

本文調用徑向基（RBF）神經網絡語句net=newrb（P，T，goal，spread，mn，df），設置目標誤差goal為10-6，初始常數spread 設置為1，最大神經元個數mn 為20，df 為1，表示每增加1 個神經元顯示一次結果，通過行車判斷實驗發現當spread 常數為1 和2 時，對正常信號可有效判斷，而對過車信號無法正確判斷，準確率分別為80%和90%，當大于等于3 時，準確率均為100%；當spread 常數為3 時，神經元個數增加到12 個時達到目標誤差算法停止，判斷結果如表3 所示。

由表3 可知，RBF 網絡20 組測試數據判斷結果中第4、13、16、17 測試組的結果均大于0.5，記為1，即過車占用信號，其余16 組小于0.5，記為0，即正常空閑信號，判斷準確率為100%。

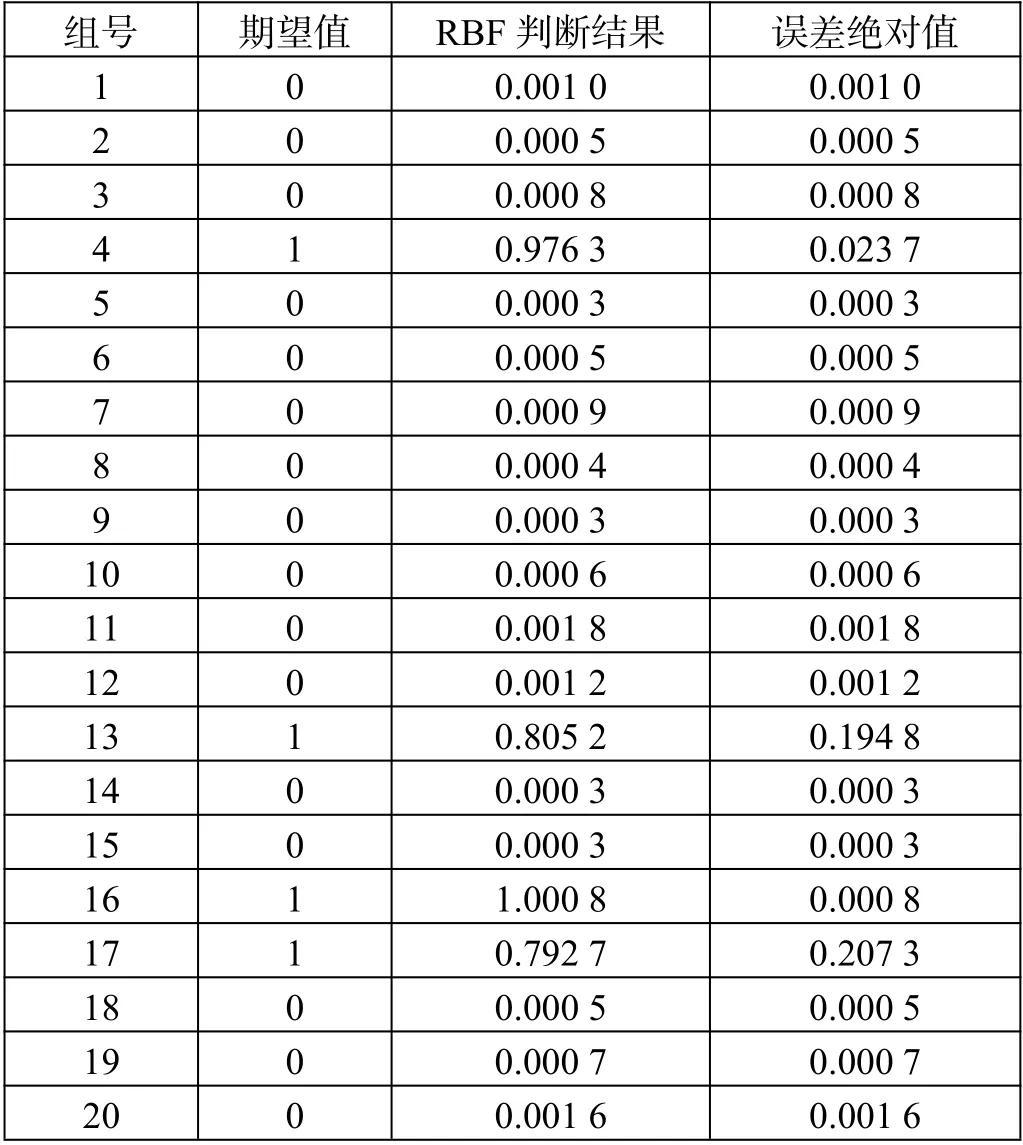
表3 RBF 模型判斷結果

6 結語

本文為了解決ZPW-2000R 型軌道電路系統中行車信號的實時判斷問題，研究了基于BP 和RBF 神經網絡的智能判斷方法。

以軌道電路系統主接收器的主機調接入電壓為輸入，列車運行狀態為輸出，將實驗采集的不同維度的實時數據補齊至相同的維度后作為神經網絡訓練的輸入，并用MATLAB 軟件編寫算法程序，通過實驗來確定模型隱藏層神經元個數、學習率、動量因子等相關參數，不斷訓練和優化網絡模型，并對模型進行回檢驗證實驗，分別建立了BP 和RBF 神經網絡模型。

將測試數據代入訓練好的模型對軌道電路行車信號進行判斷，實驗結果表明，本文提出的基于BP 和RBF 神經網絡的智能判斷方法對軌道電路主機調接入電壓行車信號判斷準確率均達到100%，從而為實際軌道電路中利用主機主接入電壓和主機調接入電壓信號聯合判斷軌道占用狀態和空閑狀態提供了一種智能方法。