垂直橫流條件下扇形氣膜孔的冷卻和流動特性分析*
石淯臣,孫震,楊柳青,何宇翔,王尊
(天津理工大學機械工程學院,天津 300384;天津理工大學天津市先進機電系統設計與智能控制重點實驗室,天津 300384;機電工程國家級實驗教學示范中心(天津理工大學),天津 300384)
燃氣輪機具有質量輕,體積小,水、電和潤滑油消耗少,起動快,自動化程度高和可以綜合利用余熱大幅度提高能源利用率等優點[1]而被廣泛應用到軍工產業當中。通過提高燃氣輪機渦輪的進口溫度,可以有效提高其熱效率。但是受到耐熱材料的限制,目前燃氣輪機渦輪的進口溫度已遠超葉片材料的耐熱極限,設計并使用高效的氣膜冷卻技術便是保證其正常高性能運行的關鍵。
影響氣膜冷卻的因素有很多[2],如主流氣體和冷氣的流動參數、冷氣/主流氣體的吹風比、氣膜孔的形狀和幾何參數等[3]。為了改善氣膜孔的冷卻和流動特性,國內外研究人員對氣膜孔的結構進行了大量的相關研究,主要集中于改變氣膜孔的幾何形狀(即設計新穎的異型孔)和在典型的圓柱孔出口處增加輔助結構兩方面。近年來,學者們在通過改善氣膜孔的形狀和幾何參數來提高冷卻效率和改善流動特性上取得了重大的突破,設計發明出了雙射流孔、同心圓孔、凹坑孔和扇形孔等多種孔型。其中,扇形孔已經被證明具有較高的冷卻效率。需要指出的是,在對上述部分孔型進行研究時,采用的冷氣流道多為冷氣腔結構,對于冷氣垂直橫流條件下的研究開展較少,而燃氣輪機渦輪動葉內部多采用垂直橫向冷氣流動與氣膜冷卻相結合的形式冷卻渦輪動葉。與通常冷氣腔結構中的冷氣流動不同,垂直橫流條件下的冷氣流動會呈現出明顯的單側偏向性,這會對不同形狀氣膜孔的冷卻特性產生不同且不可忽略的影響[4]。因此,本文將垂直橫流條件下的平板氣膜冷卻作為研究對象,采用計算流體動力學方法,對扇形氣膜孔在不同吹風比下的流場結構和冷卻效率進行分析并得出相應結論。
1 物理模型及計算設置
1.1 物理模型
所研究的扇形氣膜孔的簡圖如圖1 所示。目前所研究的孔的尺寸是直徑約為1.0 mm 的典型圓柱氣膜孔的8 倍。因此,扇形孔的孔軸長度為6D=48.0 mm,圓柱形零件部分直徑D=8.0 mm,長度為2D=16.0 mm,與主流方向的傾斜角為30°,橫向擴張角兩側相等,數值為10°(在7°~14°的典型數值范圍內)。原點位于扇形氣膜孔出口邊緣與孔中心線的交點處。坐標X、Y和Z分別表示流向、橫向和法線方向。
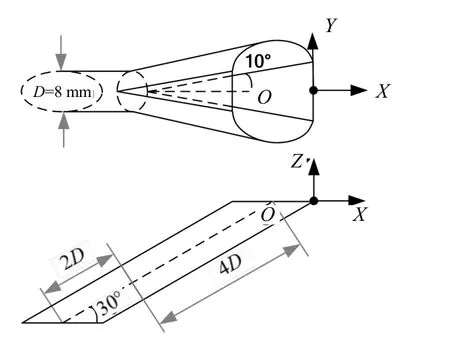
圖1 扇形氣膜孔簡圖
所研究的平板氣膜冷卻模型的前視圖如圖2所示。主流氣體流道流向長度為80D=640.0 mm,橫向寬度為3D=24.0 mm。主流流道入口與原點之間的距離為23.7D=189.6 mm。冷氣流道垂直于主流氣體流道,其橫向長度為35D=280.0 mm,流向寬度為3D=24.0 mm。主流氣體流道和冷氣流道在垂直于主流壁面的正負方向上(法線方向)的長度為15.6D=124.8 mm。扇形氣膜孔入口位于冷氣流道中點。主流氣體沿流向流動,冷氣沿橫向流動。冷氣由冷氣流道入口流入,大部分冷氣仍從冷氣流道出口流出,小部分冷氣從扇形氣膜孔入口流入主流氣體流道,在主流壁面上形成低溫氣體保護層以冷卻壁面。
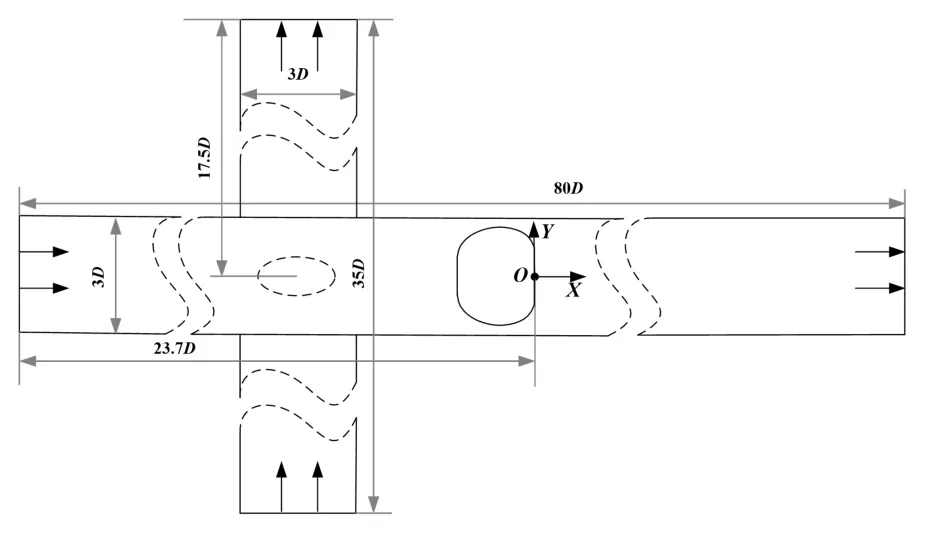
圖2 平板氣膜冷卻模型前視圖
1.2 邊界條件
設定主流氣體為理想氣體,溫度為414 K,主流氣體流道入口均勻流速為25 m/s,湍流強度為3.5%,主流氣體流道出口靜壓設置為101.3 kPa。設定冷氣為理想氣體,溫度為300 K,冷氣流道入口均勻流速為15 m/s,湍流強度為1%。計算得到主流氣體與冷氣的密度比為1.37。通過調節冷氣流道出口處的靜壓來產生特定的吹風比M,使M為0.5、1.0、1.5、2.0。主流氣體流道和冷氣流道兩側壁面均設置為對稱邊界,主流氣體流道和橫向冷氣流道的上下壁面均設置為絕熱、無滑移條件。
1.3 計算網格及方法
本文采用結構化網格進行模擬計算,網格在待冷卻壁面和扇形氣膜孔周圍進行局部加密,使y+值接近1。采用大約293 萬的網格數量作為后續模擬的網格獨立解。采用有限體積法求解雷諾平均Navier-Stokes 方程、離散連續性方程、動量方程和能量方程,離散格式采用高精格式。當所有變量的均方根殘差達到10-6時,認為仿真結果具有收斂性。采用SST 湍流模型來分析冷氣的冷卻效率及流場結構[5-6]。
2 計算結果及分析
2.1 流動特性
吹風比M為0.5 和1.5 時冷氣射流在平面X/D=5處的流線分布如圖3 所示。在吹風比M=0.5 時,冷氣射流沿孔中心線Y/D=0 形成大致相等的對稱反腎形渦對。這意味著垂直橫向冷氣流動會顯著影響孔出口下游處的流場,少量冷氣從負Y側向正Y側流動,然后在正Y側被卷入逆時針渦旋。在吹風比M=1.5 時,流場結構的非對稱性較吹風比M=0.5 時明顯增強。在吹風比M=1.5 時,冷氣的橫向流動方向是從正Y側到負Y側,與吹風比M=0.5 時相反。冷氣的橫向流動在流場中占主導地位,規模較小的逆時針渦旋出現在遠離孔中心線的區域(1.0<Y/D<1.5),而規模較大的順時針渦旋則移動到離主流壁面較遠的左上角區域(-1.5<Y/D<0.5)。

圖3 平面X/D=5 處的流線分布
2.2 冷卻特性
吹風比M為0.5 和1.5 時扇形氣膜孔的冷卻效率分布云圖如圖4 所示。冷卻效率用η表示,在吹風比M為0.5 和1.5 時,孔出口近下游區域均具有較好的冷氣覆蓋和較高的冷卻效率。在吹風比M=0.5 時,冷卻效率分布呈現雙峰且近似對稱的形狀,這與圖3 中孔出口處的速度分布保持一致。局部冷卻效率在孔出口近下游區域較高,遠下游區域較低。隨著吹風比M增大到1.5,冷卻效率分布的不對稱性逐漸增強,呈現偏向Y+側的單峰形狀。吹風比M=1.5 時的局部冷卻效率高于吹風比M=0.5 時,孔出口遠下游區域也具有較好的冷氣覆蓋。

圖4 冷卻效率分布云圖
不同吹風比下展向平均冷卻效率沿流向分布曲線圖如圖5 所示。展向平均冷卻效率用ηL表示。在較低吹風比,即M=0.5 時,緊靠孔出口下游區域具有最高的展向平均冷卻效率,約為0.64。隨著冷氣向下游的流動,展向平均冷卻效率逐漸降低至0.18 附近。展向平均冷卻效率在吹風比M為1.0 和1.5 時均呈現先上升后下降的趨勢,在吹風比M=2.0 時呈現先上升后下降再上升的趨勢,這是因為冷氣射流的出口動量較大,冷氣射流被抬離主流壁面,導致在緊靠孔出口下游區域的展向平均冷卻效率較小,隨著冷氣射流沿流向逐漸向下游流動,冷氣與主流氣體的相互摻混作用逐漸增強,冷氣射流的動量減小且向主流壁面方向下降,展向平均冷卻效率得以提高。中高吹風比條件下的展向平均冷卻效率在緊靠孔出口下游區域均低于吹風比M=0.5 時。吹風比M=1.5 時的展向平均冷卻效率在X/D=0.5 時達到最大值,在0.68 左右,之后均高于其他吹風比的展向平均冷卻效率。展向平均冷卻效率在吹風比M=1.0 時最終保持在0.20 附近,而在吹風比M為1.5 和2.0 時則最終保持在0.33 附近。
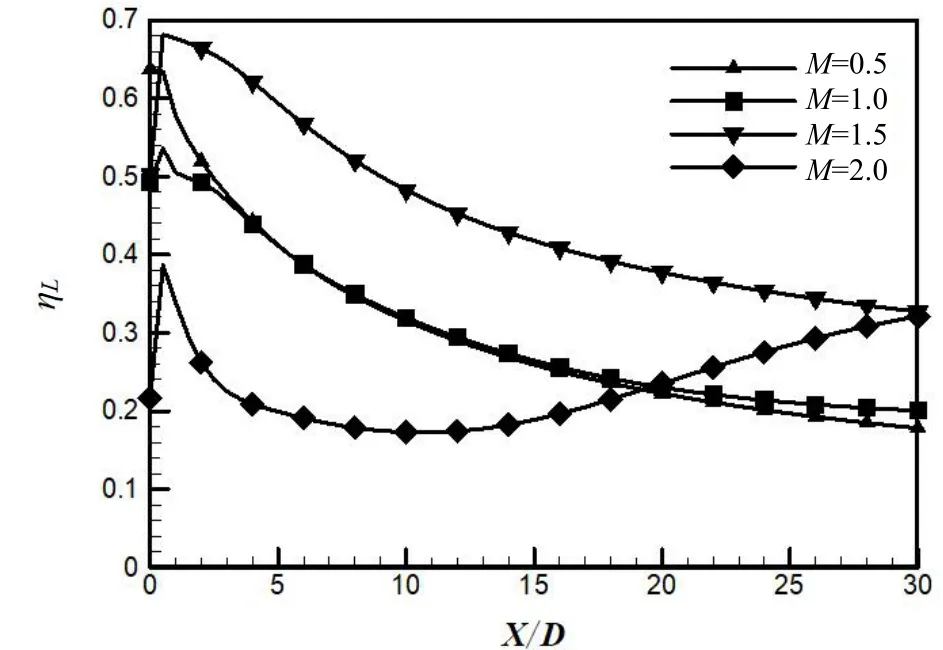
圖5 展向平均冷卻效率沿流向分布曲線圖
不同吹風比下面積平均冷卻效率的柱狀圖如圖6所示。面積平均冷卻效率用ηav表示。隨著吹風比的增加,面積平均冷卻效率呈現先增大后減小的趨勢,吹風比M為0.5 與1.0 之間的變化較小,吹風比M為1.0與1.5、1.5 與2.0 之間的變化較大,約為0.154 和0.218。面積平均冷卻效率在吹風比M=1.5 時達到最大值,約為0.454,在吹風比M=2.0 時達到最小值,約為0.236。
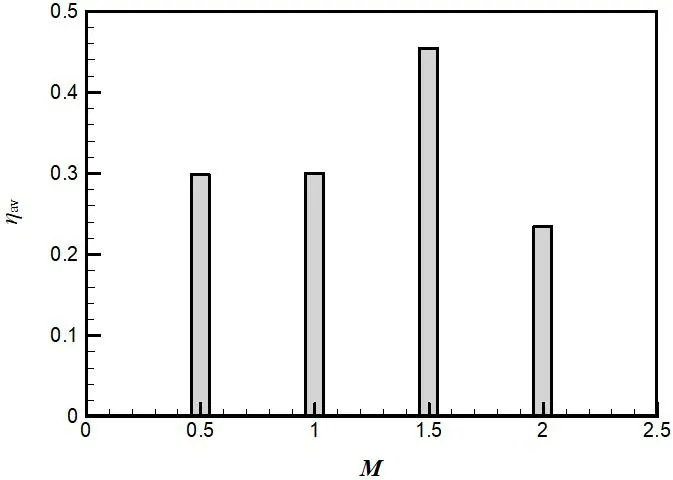
圖6 面積平均冷卻效率柱狀圖
3 結語
本文通過數值模擬的方法對垂直橫向冷氣流動條件下不同吹風比M為0.5、1.0、1.5 和2.0 時扇形氣膜孔平板氣膜冷卻的流場結構和冷卻效率進行研究分析,得到了以下結論:①吹風比M=0.5 時,冷氣射流呈現大致相等的對稱反腎形渦對,冷氣由負Y側流到正Y側;隨著吹風比增大到M=1.5,流場的不對稱性明顯增強,冷氣的流動方向與較低吹風比時相反,冷氣的橫向流動在流場中占主導地位。②吹風比M=0.5時,冷卻效率呈現近似對稱的雙峰形狀;隨著吹風比M增大到1.5,冷卻效率分布的不對稱性增強,呈現單峰形狀。中高吹風比時的局部冷卻效率和冷氣的覆蓋程度均優于低吹風比時。③展向平均冷卻效率沿流向在吹風比M=0.5 時呈現下降趨勢,在吹風比M為1.0和1.5 時呈現先上升后下降趨勢,在吹風比M=2.0 時呈現先上升后下降在上升趨勢。除緊靠孔出口下游區域外,吹風比M=1.5 時的展向平均冷卻效率最高,最大值約為0.68。在緊靠孔出口下游區域,吹風比M=0.5時的展向平均冷卻效率最高,最大值約為0.64。面積平均冷卻效率隨吹風比的增大先增大后減小,當吹風比M=0.5 時達到最大值,約為0.454。

