圓筒型永磁直線電機的磁熱雙向耦合分析

嚴 謹，蘇朝葵，毛宏勇，曹 勇，羅楊陽

1.廣東海洋大學海洋工程與能源學院，廣東 湛江 524029；

2.中廣核工程有限公司核電安全監控技術與裝備國家重點實驗室，廣東深圳 518172；

3.武漢第二船舶設計研究所，湖北 武漢 430064；

4.武漢工程大學機電工程學院，湖北 武漢430205

在石油開采領域，與傳統的旋轉電機相比，圓筒型永磁直線電機直接帶動抽油桿柱進行往復直線運動，簡化了動力傳遞過程，可以提高抽油效率，因此逐漸得到廣泛應用。

圓筒型永磁直線電機工作時需要向初級繞組通入正弦電流，在氣隙中產生行波磁場，行波磁場和次級永磁體的勵磁磁場相互作用產生電磁推力。如果初級固定，次級便在電磁推力作用下做往復直線運動［1］。為了產生滿足要求的電磁推力，通入初級繞組的正弦電流往往比較大，因而電機在工作時會產生大量的熱量，引起電機的溫度升高。溫度變化對電機的工作性能和使用壽命會有極大的影響，為了更好地改善電機的發熱和散熱問題，必須對電機進行準確的溫升分析。

對電機的溫升分析涉及到電磁場和溫度場計算，電磁場的計算一般使用有限元法，而溫度場的計算主要有簡化公式法、等效熱網絡法和有限元法［2］。簡化公式法計算簡單，但準確度低，只能粗略計算電機的平均溫升，無法了解電機的溫度分布，僅適用一些要求不高的場合。等效熱網絡法可計算出電機各部分的溫升，計算速度快且準確度高［3］，但其計算的是人為設置的各個節點的溫度，若想更全面地了解電機的溫度分布，需要增加電機溫度場的網絡節點的數量，從而導致計算量大大增加［4］。有限元法計算準確度高，邊界適應性好，可全面了解電機的溫度分布和過熱點的位置。文獻［2］分別用等效熱網絡法和有限元法對輪轂電機的溫度場進行計算，兩種方法的計算結果和實驗測量數據存在較小的差異，都在合理的計算誤差范圍內，相對而言，有限元法的計算結果誤差更小。

電磁場和溫度場目前以單向耦合為主，單向耦合比雙向耦合設置更簡單，計算更快速，但計算準確度不如雙向耦合高，因此也有文章以磁熱雙向耦合法分析電機溫升。文獻［5］提出了一種磁熱單向耦合分析方法，在電磁場中計算出輪轂電機的繞組損耗、定轉子損耗和永磁體渦流損耗，將其作為熱源導入到溫度場中，在溫度場中計算出電機的溫度分布，但沒有考慮到溫度場對電磁場的影響。文獻［6］提出了一種有限元法和熱網絡法相結合的磁熱雙向耦合方法，采用有限元法分析電磁場，熱網絡法分析溫度場，并將電磁場和溫度場相互耦合，其仿真結果比磁熱單向耦合的仿真結果更加接近實驗數據，驗證了磁熱雙向耦合法的準確性。該方法考慮了實際中溫度場對電磁場的影響，不過用熱網絡法計算溫度場得到的是各個節點的溫度，不夠直觀和全面。

為了全面且準確的計算圓筒型永磁直線電機工作時的溫度分布，本文提出了一種基于有限元法的磁熱雙向耦合分析方法：采用有限元法分析電磁場和溫度場，并將電磁場和溫度場相互耦合，該方法考慮了溫度場對電磁場的影響。

1 圓筒型永磁直線電機的參數及模型

圓筒型永磁直線電機的主要參數如表1 所示。采用SolidWork 軟件對電機進行建模，模型如圖1所示，在電磁場和溫度場中可將該模型直接導入。

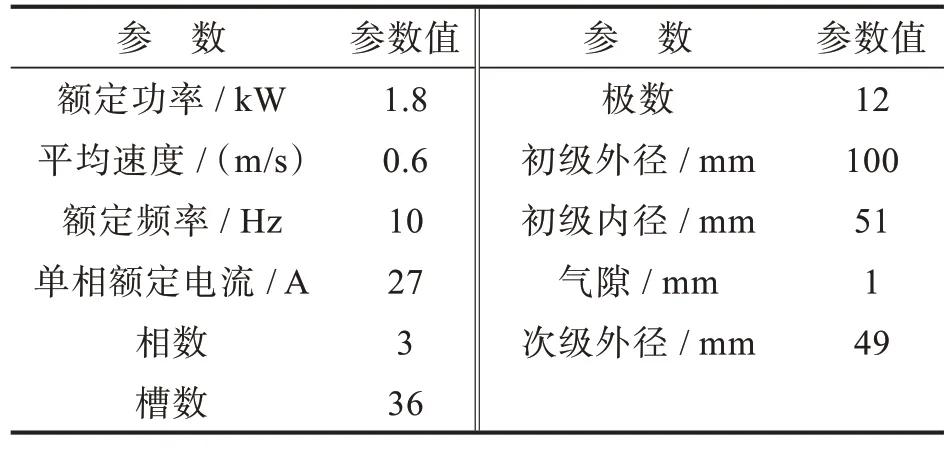
表1 電機主要參數Tab.1 Main parameters of motor

圖1 圓筒型永磁直線電機三維模型Fig.1 Three-dimensional model of tubular permanent magnet linear motor

2 能量損耗計算

電機在運行時會產生大量的熱量，熱量一般來自繞組銅損耗、定子鐵芯損耗、永磁體渦流損耗和機械損耗［7］，即

式中：PCu為繞組銅損耗，PFe為定子鐵芯損耗，Pme為永磁體渦流損耗，Pm為機械損耗。

繞組銅損耗可以根據焦耳定律求得，本文中研究的直線電機采用三相繞組，因此繞組銅損耗的計算公式為：

式中：I為每相繞組的電流有效值，R為每相繞組電阻值。

電機運行時，溫度的升高會改變電機材料的物理性質。電機的熱源損耗主要來自繞組的銅損耗，根據公式（2）可知，繞組銅損耗和銅線的電阻值成正比關系，銅線的電阻值有［8-9］：

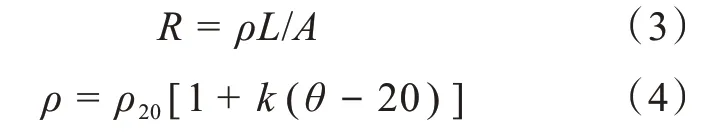
式中：R為銅線電阻值；ρ為θ℃時銅的電阻率；ρ20為20 ℃時銅的電阻率，ρ20=1.75×10-8Ω· m；k為銅的溫度系數，k=0.003 93 ℃-1；L為銅線的長度；A為銅線的截面積。

定子鐵芯損耗主要由3 部分組成，即磁滯損耗、渦流損耗和附加損耗，計算公式為［10］：

式中：Kh為磁滯損耗系數；Keddy為渦流損耗系數；Kexc為附加損耗系數；f為定子鐵芯實際磁通頻率；τ為磁滯損耗系數；Bm為定子鐵芯磁通密度最大值。

當次級作直線往復運動時，永磁體內部會感應出渦流而產生渦流損耗導致發熱，永磁體渦流損耗有［6］：

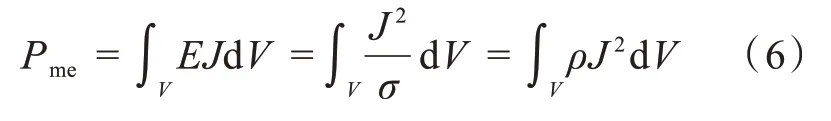
式中：σ為永磁體電導率；E為渦流電場強度；J為渦流密度；ρ為永磁體電阻率；V為永磁體的體積。

機械損耗主要來源于軸承損耗和風磨損耗，由于本文所研究電機的動子額定速度僅為0.6 m/s，因此機械損耗非常小，可以忽略不計。

3 導熱系數和對流散熱系數的計算

在直線電機中有3 種傳熱方式：熱傳導、熱對流和熱輻射。在對電機的溫度分析中，僅需考慮前兩種，熱輻射可以忽略不計。熱傳導需要確定電機各部件的導熱系數，熱對流需要確定電機各對流面的對流散熱系數。下面對這兩個系數進行計算。

3.1 導熱系數的計算

電機中除了繞組的構成較為復雜，其導熱系數需要另行計算外，其他部件的導熱系數都可由其選用的材料直接得知。

電機的繞組主要由銅導線和外包裹的絕緣材料及粘合劑組成。為了充分利用槽內空間，本電機采用矩形截面銅導線。由于銅導線均勻排列在初級槽內，可以把銅導線和聚亞安酯等效地看作一個導熱體，為等效銅繞組；環氧樹脂和槽絕緣層近似看作另一個導熱體，為等效絕緣層。等效模型如圖2 所示［11］。

圖2 繞組線圈結構及其等效模型Fig.2 Winding coil structure and its equivalent model

多層導熱體的等效導熱系數為［12］：

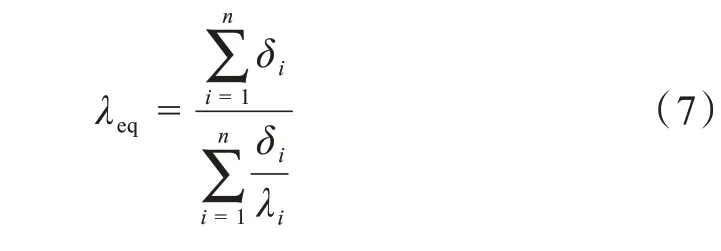
式中：λeq為等效導熱系數；δi為各導熱體的厚度；λi為各導熱體的導熱系數。

式中：Cp為等效比熱容；ρ為等效密度；V為等效體積；Ci為各導熱體的比熱容；ρi為各導熱體的密度；Vi為各導熱體的體積。

根據公式（7）～（8）可以計算出等效銅繞組和等效絕緣層的導熱系數以及比熱容。電機主要部件的材料熱屬性如表2 所示。

表2 材料熱屬性Tab.2 Thermal properties of materials

3.2 對流散熱系數的計算

電機在空氣中運行時，其散熱方式主要是與空氣進行對流散熱，因此需要準確計算出各對流面的對流散熱系數。電機的對流面有初級外表面和氣隙表面。

根據文獻［14］可知，電機初級外表面的對流散熱系數α=14.2 W（/m2·℃）。電機氣隙表面的對流散熱系數可由下列公式計算得到［15］：

式中：Re是雷諾數；v為空氣流速；D為當量直徑；γ為空氣的運動黏性系數；Nu是努謝爾數；Pr為空氣的普朗德數；L為電機初級軸向長度；α為對流表面的散熱系數。通過計算可得電機氣隙表面的對流散熱系數α=53.5 W（/m2·℃）。

4 實例分析

4.1 仿真分析

分別采用磁熱雙向耦合與單向耦合的方法對電機進行仿真，在兩種耦合方式下，電機的各項損耗如表3 所示。根據仿真結果可知，電機發熱主要是由于繞組銅損，無論單向耦合還是雙向耦合，定子鐵芯損和永磁體渦流損耗都很小，因為該電機的激勵電流的額定頻率僅為10 Hz，動子的平均運動速度僅為0.6 m/s。相比單向耦合，雙向耦合的銅損耗有較大的提升，因為溫升會造成銅導線電阻率的增大；鐵芯損耗和渦流損耗變化不大，因為其數值太小，溫度的上升對其影響不大。

表3 電機的各項損耗Tab.3 Motor losses W

兩種耦合方式計算的損耗有較大的差異，這將導致溫度場計算結果的不同。兩種耦合方式下電機穩定運行時的溫度分布云圖如圖3 所示，圖4是電機各部件的穩態溫度。

由圖3 可知，在兩種耦合方式下，電機的最高溫度都出現在中部區域的繞組處，因為繞組銅損耗是電機的主要熱源。由于中間區域的散熱比兩端要差些，因此沿軸向方向電機整體的溫度分布呈現中間高兩邊低的特點。電機各部件的穩態溫度如圖4 所示，由于雙向耦合的總損耗高于單向耦合的總損耗，因此雙向耦合下電機各部件穩態溫度均高于單向耦合仿真的結果。同時由于繞組銅損耗是電機損耗的主要來源，繞組溫度的變化幅度最大。

圖3 電機溫度分布云圖：（a）單向耦合，（b）雙向耦合Fig.3 Cloud diagrams of motor temperature distribution：（a）unidirectional coupling，（b）bidirectional coupling

圖4 電機各部件的穩態溫度Fig.4 Steady-state temperatures of each part of motor

繞組和永磁體是決定電機性能的部件，溫度過高會破壞繞組的絕緣性能以及減弱永磁體的磁性能，因此需要重點關注繞組和永磁體的溫度變化，下面用磁熱雙向耦合法對繞組和永磁體進行溫度分析。

(2)開展基金保值、增值工作，提高資金的運作能力。我國公募、非公募體育基金會在資金來源方面已有明顯差異，非公募體育基金會相對來說資金來源渠道和政府補貼少，更需要對基金做好保值、增值工作。體育基金會可以通過資本運作的方式進行投資，從而獲得投資收益，一方面實現資金的保值、增值，另一方面為體育公益項目提供更加穩定、更加豐富的資金來源。體育基金會還要加強與銀行等金融機構的合作，利用金融機構成熟的運作模式為體育基金會資金運作提供技術保障，同時依托體育基金會的公益平臺促進金融機構社會責任的履行。

圖5 是電機繞組和永磁體的最高溫度隨時間變化的曲線圖，可以看出，在電機運行后的前4 000 s內，電機的繞組和永磁體的溫度上升得很快，這是因為當電機剛剛運行時，電機產生很大的損耗，而電機的散熱是很小的。在4 000 s 后電機產生的熱量和散發到周圍環境的熱量將趨于一致，繞組和永磁體的溫度上升變慢，最終電機的溫度會達到一個平衡穩定的狀態。

圖5 繞組和永磁體的溫度隨時間變化的曲線Fig.5 Temperature changes of winding and permanent magnet with time

定子和動子的溫度沿軸向位置變化的曲線圖如圖6 所示。沿軸向方向定子和動子的溫度總體上呈現中間高兩邊低的特點。動子由永磁體和導磁套交替嵌在軸上而成，由于永磁體和導磁套的導熱性能相差不大，因此動子的溫度曲線很平滑。定子的溫度曲線呈波浪狀，波峰代表了繞組的溫度，波谷代表了絕緣層和定子鐵芯齒部的溫度，這表明包裹在繞組外的絕緣層有很好的絕熱性，阻隔了繞組的熱量向外部擴散。為了改善繞組的散熱問題，可以在繞組槽上涂抹一層導熱膠。

圖6 定子和動子的溫度沿軸向位置變化的曲線Fig.6 Temperature changes of stator and actuator along axial position

4.2 試驗結果分析

對圓筒型永磁直線電機的溫升進行實驗分析，實驗裝置主要由直線電機、往復抽油泵、過濾器、蓄能器、溢流閥、壓力表、壓力傳感器及溫度傳感器等組成。直線電機的負載是往復抽油泵，往復抽油泵的負載是溢流閥回路，模擬電機的實際工況。溫度傳感器預埋在電機的定子和動子中，分別測量繞組和永磁體的溫度。

每隔30 min 記錄一次數據，記錄2.5 h，此時電機已達到熱平衡狀態。圖7 為仿真與試驗的結果對比，可以看到，仿真結果和試驗結果曲線的趨勢是基本相同的，但電機穩定運行時的結果數值有所差異，繞組處單向耦合的誤差為21.5%，雙向耦合的誤差為8.56%；永磁體處單向耦合的誤差為21.2%，雙向耦合的誤差為8.98%。

圖7 仿真結果與試驗結果對比：（a）繞組，（b）永磁體Fig.7 Comparisons between simulation results and test results：（a）winding，（b）permanent magnet

經過分析，產生誤差的原因有：

（1）測量過程存在誤差，且有限元模型的邊界條件假設和網格剖分質量也會產生誤差。

（2）磁熱單向耦合仿真中，電機各部件的材料參數如銅線的電阻率、永磁體的剩磁等均采用20 ℃時的數值，不隨溫度變化而改變，因此當電機的穩態溫度較高時，誤差會較大。

（3）采用磁熱雙向耦合法時，銅線的電阻值隨溫度上升而增大，根據公式（2）可知銅損會增大，但在實際中，電阻值的增大還會導致銅線上的電流減小，因此計算的銅損值會高于實際的銅損值，計算溫度也會高于實際溫度。

相較于磁熱單向耦合，磁熱雙向耦合仿真結果的誤差大大降低，能夠滿足工程要求，表明了磁熱雙向耦合的準確性。電機的繞組絕緣采用C 級絕緣，永磁體采用N35UH 燒結釹鐵硼。C 級絕緣的最高允許溫度為180 ℃以上，溫升極限為140 ℃以上，繞組的最高測量溫度為159.61 ℃，可以保證絕緣材料不容易老化。永磁體的最高測量溫度為141.44 ℃，低于N35UH 燒結釹鐵硼的最高工作溫度180 ℃，永磁體不會發生嚴重退磁。表明電機在額定工況下使用時，產生的溫升不會影響其正常的工作性能，電機能夠長期且穩定的運行。

5 結論

針對圓筒型永磁直線電機的溫升問題，提出了一種磁熱雙向耦合方法，分析了電機的溫度分布以及過熱點的位置。繞組和永磁體是決定電機性能的主要部件，溫度過高會破壞繞組的絕緣性能以及減弱永磁體的磁性能，因此重點分析了繞組和永磁體的溫度變化。通過電機溫升試驗，驗證了磁熱雙向耦合法分析電機溫度場的準確性，可為電機的材料選型與熱平衡設計提供參考。