基于教與學策略的動態變異花授粉算法①

段艷明,肖輝輝,譚黔林,趙翠芹

(河池學院 大數據與計算機學院,河池 546300)

1 引言

學者Yang 受顯花植物繁殖機理的啟發,提出了一種名為花授粉算法(flower pollination algorithm,FPA)[1]的智能優化算法.該算法仿生原理簡單、參數較少、易調節,運用轉換概率參數p好地解決了探測和開采之間的平衡問題.當前,FPA 算法主要在函數(包括無約束函數和約束函數)優化、能源、通信等應用領域得到了廣泛運用,其具體應用如下:

(1)函數優化領域

函數優化是屬于連續優化問題,可分為無約束函數優化和帶約束的函數優化.郭慶等[2]分析了FPA 算法在求解多模態優化問題時存在的不足,分別利用模擬退火和單純形法思想對FPA 算法的全局搜索和局部搜索進行了改進了,設計出一種新的FPA 算法框架;最后,利用改進算法對多種類型的測試函數進行求解,并與對比算法進行了對比分析,實驗結果說明改進算法是一種具有良好競爭力的新算法.

(2)能源領域

能源是一個國家的經濟命脈,如何提高能源的利用率是一個熱點的研究話題.為此,眾多學者運用元啟發式算法來解決該問題,并取得不錯的效果.如用FPA算法對能量流管理[3]、能源交易市場單價預測[4]、電力調度[5]等問題進行優化求解,并獲得較好的結果.

(3)通信領域

Rajeswari 等[6]把鮑威爾法引入到花授粉算法中,并用改進的花授粉算法解決傳感網最小能量傳播問題,實驗結果表明新算法與對比算法相比,更適合解決此類優化問題.

雖然該算法在眾多領域中得到了廣泛應用,但該算法與其他智能算法一樣,也存在一些不足,如算法演化后期計算速度慢、容易早熟,尋優精度不高,魯棒性差等缺陷,導致其在解決大量復雜優化問題時獲得的結果不盡人意.為了克服這些算法存在上述的不足,提高其收斂能力,當前眾多學者依據各種智能算法的特征和優缺點,運用了諸多的策略和方法對其進行了改進,構建了許多優化能力更強的新算法模型,使得大量的工程優化問題得到更好的解決.

Zhou 等[7]在FPA 算法的勘探部分融入精英反向學習策略的組合探測搜索機制,以增加個體之間的差異性,擴展算法的探索領域; 在算法的開發部分加入貪婪搜索機制構造新的局部搜索策略,以提高算法的開采能力; 同時對參數p運用了動態調整策略.實驗結果表明改進算法的尋優能力得到了一定提升.一方面,該算法利用精英所具有的豐富信息,可有效提升算法的性能; 另一方面,在該算法演化過程中,由于精英起著重要作用,將引導種群快速向最優解靠近,因此,若精英一旦陷入局部極值,則導致整個種群停滯進化,易造成算法陷入“早熟”問題.

Abdel-Raouf 等[8]把particle swarm optimization(PSO)算法融合到FPA 算法中,即把PSO 算法優化后的種群作為FPA 算法的初始解,同時通過混沌映射對算法的參數進行調節,這使算法解的質量得到了改善,但該算法由于缺乏增加種群多樣性機制,使其在演化中種群的多樣性不能得到較好的保持,易陷入局部最優.Lenin 等[9]先對和聲算法增加混沌策略進行改進,再把其優化后的種群作為花授粉算法的初始解,提高算法初始解的質量,提升了算法的尋優性能,但其同樣存在文獻[8]的不足.

Tawhid 等[10]利用鯨魚優化算法的搜索獵物策略和攻擊獵物方法替換了FPA 算法的全局搜索策略,構建了一種新的混合算法whale optimization algorithm and flower pollination algorithm (WOFPA),其性能與對比算法相比,得到了一定程度的提升,但該算法增加了較多的參數,降低了算法的靈活性,同時新算法只在低維上驗證了其性能的優越性,沒有在高維得到驗證,使其缺少了說服力.

Draa[11]對FPA 算法進行了定性、定量分析及其改進.首先,從改進的FPA 算法文獻中所利用的測試函數、實驗驗證方式及傳統FPA 算法參數值的設置3 個方面進行了詳細的定性分析; 其次,依據定性分析的結果,作者對參數p的值設置進行了較全面的實驗對比分析,分析結果表明當p的值取0.2 時,該算法的尋優能力獲得最佳; 最后,根據上述的定性分析和定量分析實驗,作者把反向學習方法引入到該算法中以達到提高其尋優能力,優化結果說明該改進策略是行之有效的.但是,反向學習機制對算法的改善還是很有限的,其原因在于學習機制過于簡單,不能很好地提取和利用較劣粒子所隱含的有益信息[12]; 同時在進化后期,大部分反向點及原點都集中到小范圍區域,使反向點的適應度值并不比原值較優,所以在演化后期試圖通過反向的方式很難跳出當前的極值區域[13],其依然不能解決算法陷入局部最優、收斂精度低的問題.另外,在該算法中是以一定概率采用反向學習策略,擴大了算法的隨機性,從而減緩了其收斂速度.

綜上所述,目前的一些改進方法對FPA 算法的優化能力起到了一定的提升作用,但這些方法沒有對種群個體之間的信息進行有效利用,造成種群的多樣性在演化過程中不能較好地保持,使算法易“早熟”,影響了其全局優化能力; 同時,當前改進的FPA 算法在對多模態等復雜問題進行求解時,其求解精度、穩定性及求解速度等方面還有較大的提升空間,且有些改進措施增加了算法的時間復雜度,降低了算法的靈活性,另外一些改進策略對基本的FPA 算法原有的仿生原理做了相應的修改.

為了解決在提高算法的收斂速度、解的質量的同時防止算法“早熟”的問題,本文構建了一種把改進的教與學優化算法[14]中的教與學思想及動態高斯變異融入到花授粉算法中的改進算法(teaching learning Gauss flower pollination algorithm,TLGFPA).

TLGFPA 算法的基本思想: 首先,根據總迭代次數與當前迭代次數的關系對教與學優化算法中的教學因子進行改進,并把改進的教機制作用于花授粉算法中的全局尋優部分,充分利用最優個體(教師)與其他個體(學生或學員)間的促進作用來提高算法的收斂速度;其次,把教與學優化算法中的學機制作用于花授粉算法中的局部尋優部分,通過個體(學生或學員)之間的相互學習來保持種群的多樣性,提高其求解精度; 最后,在教與學優化算法的教階段的進化過程中,由于超級個體(教師)不斷吸引其他普通個體(學生),使得種群個體之間的差異性不能到較好的保持,從而易造成算法“早熟”,因此,在進化過程中需要判斷算法是否陷入“早熟”進行處理,若“早熟”,則利用動態高斯變異策略對種群的中間個體進行擾動,增加種群個體之間的差異性,防止算法過早收斂.

首先,通過對16 個經典的優化問題進行求解,求解結果顯示新算法與FPA 算法相比,其優化能力得到了較顯著提升; 其次,選擇了3 種FPA 改進算法進行了對比實驗,對比分析結果顯示新算法的性能總體上要好于對比算法,顯示出較好的競爭力.最后,運用TLGFPA 算法對伸縮繩應用問題進行求解,同樣也得到了較好的優化結果,進一步驗證了TLGFPA 算法的有效性和可行性.

本文的創新工作主要包括:

(1)為了解決教學機制容易導致教與學算法“早熟”問題,本文對該算法的教學因子進行改進,使其隨著迭代的進行而動態調整,能夠較好地解決其的勘探和開采能力平衡問題.

(2)把改進的教機制作用于花授粉算法中的全局尋優部分,充分運用最優個體(教師)與其他個體(學生或學員)間的促進作用來提升算法的搜索速度; 同時把教與學優化算法中的學機制作用于花授粉算法中的局部尋優部分,通過種群個體之間的相互交流學習來維持種群的多樣性,改進其求解精度.

(3)在算法中融入了動態高斯變異策略來提高種群個體之間的差異性,防止算法“早熟”而導致整個種群進化陷入停滯狀態.

本文第2 節對FPA 算法進行了簡單描述; 第3 節對教與學優化算法、改進的教與學優化算法、動態高斯變異機制、TLGFPA 算法以及該算法的時間復雜度進行了闡述; 第4 節進行實驗評測; 第5 節對本文的研究工作進行歸納,并對今后的研究方向進行展望.

2 FPA 算法

該算法的仿生原理是對花朵植物繁殖過程(異花和自花授粉)的模擬,花朵植物的異花授粉過程是通過昆蟲等方式來實現授粉繁殖,具有萊維飛行的特征,FPA 算法的全局搜索策略模擬了該過程,這使其具有良好的全局優化能力,花朵植物的自花授粉是通過同株上的花朵自行傳粉繁殖,傳播距離非常小,這個過程對應于FPA 算法的局部搜索過程.同時,該算法運用參數p來解決其的勘探和開采能力平衡問題,這使其具有較好的全局尋優能力.為了利用該算法更好地解決一系列實踐中復雜的優化問題,還必須對其設定4 條約定,其詳情見文獻[1].依據上述思路,學者Yang[1]利用以下公式對其實現了數學模型化.

FPA 算法的探索機制(全局搜索策略)是采用式(1)進行模型化:

其中,,表示算法進化中第t、t+1 代對應的解,g*表示種群中的最優個體,γ是對步長進行控制的伸縮因子,L(λ)表示種群個體的Lévy 步長,其值運用式(2)計算:

其中,λ取值1.5,G(λ)表示Gamma 函數,s的值通過式(3)計算得到:

其中,μ～N(0,σ2),V～N(0,1),σ2的值采用式(4)計算:

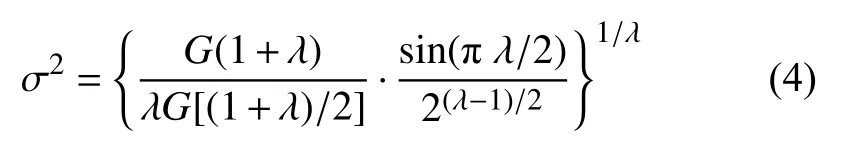
FPA 算法的種群個體采用式(5)實現開發搜索(局部搜索):

其中,ε∈[0,1]上產生的隨機數,xtj,xtk是隨機選擇的不同于xti的兩個不同的種群個體.

3 教與學優化策略的動態變異花授粉算法

3.1 教與學優化算法

受教與學的啟發,Rao 等[14]設計了一種名為教與學優化算法(TLBO),該算法模擬了教師的教學過程及學生之間的相互學習和交流的過程.該算法的種群個體分為教師和學生兩類,教師是超級個體,學生是普通個體,其所學科目數對應問題的維數.TLBO 算法把進化過程分為“教學”與“學習”兩個時段,在“教學時段”是普通個體(學生)向最優個體(教師)不斷學習的過程,從而達到提升學生的成績,同時結合了種群均值的作用,能有效地融合最優個體與普通個體的相互促進作用; 在“學習時段”,隨機選取兩個種群個體,并比較其優劣,劣者向優者學習.

教與學優化算法的具體實施過程如下.

Step 1.對算法種群(班級)個體的位置利用式(6)進行隨機初始化:

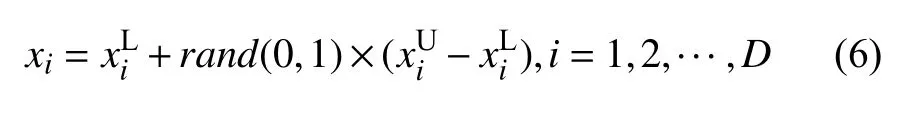
其中,和分別為解空間自變量xi的上界和下界,D為解空間的維數,rand(0,1)∈(0,1)之間的任意數.

Step 2.教學時段.每個普通個體(學生)通過最優個體(教師)和學生平均值之間的差異來向教師(最優個體)學習,首先求解當前種群每一維的平均值xmean,再利用式(7)計算教師與學生的差異,最后利用式(8)實現位置更新,即完成教的過程:

其中,xteacher是種群中的超級個體,s=rand(0,1)為學習步長,tf=round(1+rand(0,1))為教學因子.

Step 3.對普通個體(學生)位置進行更新.每個學生依據學習的效果決定對當前的位置是否更新,若優對其當前位置進行更新,否則保留其原有位置.

Step 4.學習時段.對種群中每個普通個體(學生)xi,隨機選取其學習對象xj(i≠j)進行學習,通過計算兩者間的目標函數適應度值來進行調整位置,即利用式(9)來進行學生間的學習:

其中,f(xi)和f(xj)分別表示個體xi和xj的目標函數適應度值,s=rand(0,1)為學習步長.

Step 5.對普通個體(學生)位置進行更新.每個學生依據學習的效果決定對當前的位置是否替換,若優,替換,反之保留原有位置.

Step 6.對算法的演化條件進行判斷,如條件成立,則優化結束,并輸出算法的最優值和其對應的最優解,否則進化繼續并轉Step 2.

3.2 動態高斯變異

高斯分布是一類重要的概率分布函數,在眾多領域得到廣泛應用,其計算公式如式(10):

其中,σ、μ為分別表示為方差為1 和均值為0.

動態高斯變異的思想是給原有個體增加一個擾動項,其具體形式如下:

其中,m=(Max_iter-t)/Max_iter,即m∈(1,0]為遞減變量;xi表示為算法在進化代數為t時個體i所對應的狀態;N(0,1)是服從高斯分布的一個任意向量;Max_iter表示算法的最大進化代數,t表示為算法當前進化的代數.

動態高斯變異機制能在一定程度上增加了種群個體之間的差異性,能使個體有效跳出局部極值進行全局搜索,同時提高收斂速度.

3.3 改進的教與學優化機制

3.3.1 TLBO 算法存在的問題

根據第3.1 節可知,TLBO 算法主要由“教學時段”和“學習時段”兩個核心部分構成,但由于該算法的搜索機制存在以下問題,使其優化能力受到一定的影響:

問題1.在TLBO 算法的教學時段,教學因子tf左右著學生個體與教師個體的差異,tf的大小決定著算法在該階段的搜索能力,tf越小,則搜索能力越強.但從基本TLBO 算法的教學因子的計算公式可知,其值隨機地在[1,2]中取值,沒有考慮到隨算法的進化而相應地調整該值,從而使教學階段易陷入兩種極端的狀況,學生要么學得很好,要么學得很差,但在實際的教學過程中,學生個體是以任何概率從教師處學到知識.而且,在教學前期,學生個體與教師個體的差距是較大的,到教學后期,學生個體與教師個體的差距就會不斷縮小.

問題2: 從TLBO 算法的教學階段可知,通過普通個體(學生)之間小范圍的相互交流學習來提升各自的成績,這使種群個體之間的差異性能夠得到較好的保持,從而保證了算法的持續全局尋優能力.但是,在TLBO 算法的教學階段,每個學生(個體)都向教師(最優個體)學習,雖然能快速提高搜索速度,但更易導致種群陷入局部最優.

3.3.2 對TLBO 算法進行改進

(1)對TLBO 算法的教學因子tf進行改進

針對第1 個問題,本文對教學因子tf做了改進,使其隨著迭代的進行而線性遞減,把教學因子tf的計算公式修改為:

其中,tfmin是tf取的最小值,tfmax是tf取的最大值,N_iter、t分別表示為算法的最大進化代數和當前進化的代數.

從式(12)中可以看出,tf的值在算法進化的前期取值較大,這有利于學生的學習速度和學習能力的提高,從而達到提升算法的勘探能力,提高算法的尋優速度; 在算法進化的后期,學生的學習速度和學習能力顯著下降,教學因子tf的值變小,有利于提高算法的開采能力,促進種群個體向理論解靠近,提高解的精度.

(2)融入動態高斯變異機制

針對問題2,本文把高斯變異機制融入到TLGFPA算法中,從而進一步改善算法的優化能力.這是因為TLGFPA 算法的全局授粉部分引入了TLBO 算法的教機制,而TLBO 算法的教階段在進化過程中,由于超級個體(教師)不斷吸引其他普通個體(學生),使得種群個體在進化過程容易同化,從而易造成算法陷入局部最優.為此,在進化過程中需要對算法是否陷入“早熟”進行判斷,若“早熟”,則利用動態高斯變異策略對種群的中間個體進行擾動,增加種群個體之間的差異性,防止算法過早收斂.

3.4 TLGFPA 算法

從式(1)可知,FPA 算法采用了Lévy 策略使其具有良好的勘探能力,但該策略也使其求解精度較低及收斂速度慢; 而其局部搜索部分利用了差分進化(DE)思想,這使其在解決高維復雜的優化問題時,性能比較差; 同時,跟其他群智能算法類似,該算法在演化的后期,隨著種群多樣性的減少,算法容易早熟.然而該算法運用轉化概率參數p來平衡該算法的勘探和開采能力.“教與學”優化算法(TLBO)是最近提出的一種新群智能算法,根據其仿生機理,其具有極強的收斂能力且求解速度快、精度高優點,但該算法的教階段使算法易陷入早熟,且其“探索”與“開采”能力之間的平衡問題沒得到較好的處理.依據兩種算法的結構及特性,把TLBO 算法引入到花授粉算法中,使其取長補短,提高算法的性能.鑒于此,本文提出了融合教與學優化策略的動態變異花授粉算法TLGFPA,先根據總迭代次數與當前迭代次數的關系對教與學優化算法中的教學因子進行改進,接著把改進的教機制作用于花授粉算法中的全局尋優部分,充分利用最優個體與其他個體間的促進作用來提高算法的搜索速度; 同時把教與學優化算法中的學機制作用于花授粉算法中的局部尋優部分,通過種群個體之間的相互交流學習來維系種群的多樣性,提高其計算精度; 最后,如果適應度值連續迭代3 次沒有改進或改進很小,則對進入下一代的中間種群個體進行動態高斯變異,增強種群的多樣性,避免過早收斂.通過融合多種策略,提高算法的尋優性能.

TLGFPA 算法的偽代碼如算法1 所示,其中,n為種群規模,p是算法的全局搜索和局部搜索之間的轉換概率,N_iter是算法的最大進化代數,ε∈[0,1]的任意數,fmin為種群個體中的最優值,g*為最優解,fitness 為函數適應度值,xi為種群的第i個體.

算法1.TLGFPA 算法偽代碼1.初始化所有參數2.for i=1: n 3.隨機產生 n 個個體 {xi | i=1,2,…,n};4.計算每個個體或每個解的適應度值;5.end 6.計算當前種群的最優值7.找出當前種群最優值對應的最優解;8.% TLGFPA 算法開始迭代9.for t=1: N_iter (總的迭代次數)do 10.for i=1: n do 11.if p＞rand(0,1)then 12./*全局尋優*/13.根據式(10)計算 tf 的值;14.計算種群個體的平均值 Solmean;15.根據式(7)計算 dif 值;

16.根據式(1)和式(8)產生一個新的候選解;xt+1 i xt+1 i 17.對 進行越界判斷18.else 19./* 局部尋優*/xtj xtk 20.隨機產生兩個個體 和 ;xt+1 i 21.根據式(9)產生一個新的候選解;xt+1 i 22.對 進行越界判斷23.end 24.找出當前種群的最優值和其對應的最優解fun(xt+1 i))25.if (t＞=3 && abs((-))＜δ)|| (t＞=3 && abs((-))=0)26.高斯變異xt+1 i fun(xti))fin(xti fun(xt+1 i 27.對 進行越界判斷28.找出當前種群的最優值和其對應的最優解29.end 30.end 31.end

TLGFPA 算法的實現過程如下.

步驟1.對TLGFPA 算法的種群規模n,全局和局部搜索轉換參數p,最大進化代數N_iter,問題規模D,教學因子的最大值tfmax,教學因子的最小值tfmin,分別進行賦值.

步驟2.對算法的種群進行初始化,求解每個解的值,并記錄所有值中的最小值或最大值和其相應的解.

步驟3.若p＞rand(0,1),利用式(12)計算教學因子tf的值.

步驟4.計算種群的平均位置Solmean.

步驟5.運用式(7)計算最優花朵與種群的差異dif.

步驟6.利用式(1)、式(8)對花朵個體的位置進行更新,并對新產生的解是否超出解的范圍進行處理.

步驟7.如果p＜rand(0,1),根據式(9)對花朵個體的位置進行更新,并對新產生的解是否超出解的范圍進行處理.

步驟8.對步驟6 或步驟7 產生的新個體進行求解,并更新fmin和g*.

步驟9.如果連續3 次,適應度值沒變或變化很小,則執行步驟10,否則跳到步驟11.

步驟10.對種群中間個體進行動態高斯變異.

步驟11.如進化代數大于閾值N_iter,則進化結束,并輸出所有解中的最優解和其相應的適應度值,否則,轉步驟3 繼續進化.

3.5 TLGFPA 算法的時間復雜度分析

改進措施對算法性能的提升是否可行,主要從兩個方面來衡量: (1)改進策略能較好地改善算法的性能;(2)改進算法的靈活性要好,且算法的時間復雜度值要小.算法的時間復雜度與其進化代數成正比例.倘若f(x)為求解的問題,D為求解問題的規模,則依據算法時間復雜度的求解原則和FPA 算法的優化機理,FPA算法的時間復雜度表示為:T(FPA)=O(D+f(D)).從TLGFPA 算法的具體實現過程可知,步驟3-步驟7 和步驟9 是新算法添加的步驟,即包括計算教學因子tf、計算種群的平均位置Solmean、計算最優花朵與種群的差異dif、更新花朵個體的位置和動態高斯變異.依據上述公式的闡述和時間復雜度的求解規則,則可推導出TLGFPA 的時間復雜度表示為:T(TLGFPA)=T(FPA)+T(計算教學因子)+T(計算種群的平均位置)+T(計算最優花朵與種群的差異)+T(更新花朵個體的位置)+T(高斯變異)=O(D+f(D))+T(1)+T(1)+O(D+f(D))+O(D+f(D))+O(D+f(D))=O(D+f(D)).從上述對改進算法的時間復雜度理論分析結果可知,改進算法與FPA 算法相比,其時間復雜度基本相同.

4 實驗仿真及分析

4.1 測試函數仿真及分析

為了驗證本文算法的可行性和有效性,本節選用4 類共16 個非常具有代表性的測試函數進行實驗,其具體詳情見表1.本節實驗除了與FPA 算法比較外,還與人工蜂群(artificial bee colony,ABC)算法[15]、動態領域學習粒子群(dynamic neighborhood learning particle swarm optimizer,DNLPSO)算法[16]、TLBO 算法、基于教與學的花授粉算法(teaching learning flower pollination algorithm,TLFPA)進行比較.實驗中所有參數的具體設定為: 種群規模n=30,最大進化代數MaxN_iter=5000,FPA、TLFPA 和TLGFPA 三種算法的p的值都取0.2; DNLPSO 算法的其他參數值來自文獻[16]; ABC 算法中,limit=100.

表1 本文使用的實驗測試函數

4.1.1 固定迭代次數的性能比較

為了驗證本文算法的有效性,佐證其收斂精度(解的質量)的優越性,且能較好地防止陷入局部最優,所有算法在每個求解問題上都獨自執行30 次,求解出其對應的Mean error (尋優均值偏差)、St.dev (標準方差)值,并為了判定TLGFPA 算法與其余5 種對比算法尋優性能是否存在顯著性差異,利用非參數統計檢驗(α=0.05 的Wilcoxon 檢驗)分別對16 個函數的實驗結果進行統計分析,其分析結果見表2,其中符號“?”,“≈”,“?”分別說明TLGFPA 算法的尋優精度遜于、相當于和高于其余算法,“w/t/l”符號分別說明TLGFPA算法與對比算法對比,在求解問題上,有w個的優化結果好于比較算法,有t個的尋優結果與比較算法相當,有l個的優化效果劣于比較算法.

表2 在固定進化代數下算法的尋優能力對比(D=30,4,2)

對表2 分析獲得,TLGFPA 算法與ABC,DNLPSO,TLBO,FPA 及TLFPA 算法相比,有8 個函數能找到理論最優值,3 個函數找的值接近理論值.與TLFPA 算法相比,只有在函數F07 上,尋優均值偏差要劣于對比算法,說明加入“動態高斯變異”策略,能使算法避免陷入局部最優,提高了算法的收斂精度,同時也提升了算法的魯棒性.與ABC,DNLPSO,TLBO 及FPA 算法比較,在16 個函數上,分別有12、15、14、15 個函數的尋優均值偏差要好于對比算法,這說明TLGFPA 算法的優化精度明顯優于對比的算法,驗證了本文提出的新算法是可行有效的,達到了改進的目的.

為了佐證新算法在高維函數上的優化能力同樣表現出色,表3 列出了6 種算法在14 個函數上D=100 的優化結果,并對實驗結果從數學角度進行統計分析.從表3 可以獲得,TLGFPA 算法有7 個函數能找到理論最優值,2 個函數找的值無限接近理論值,與TLFPA 算法相比,只有函數F03 和F07 的尋優均值偏差要遜于該算法,與其余4 種算法對比,本文算法的求解精度優勢較顯著.

表3 6 種算法在固定迭代次數下的尋優性能比較(D=100)

綜上所述,本文提出的新算法在4 類不同求解問題上的尋優能力與對比算法相比,其優化能力要優于對比算法,也說明本文算法能較好地解決“早熟”問題.

4.1.2 固定尋優精度的性能對比

為了比較TLGFPA 算法的穩定性和尋優速度,在尋優精度固定下,檢驗其收斂速度和魯棒性的優越性,其實驗結果如表4 所示.本節所有算法在每一個求解問題上都設置了一個固定的尋優精度邊界值,若算法收斂到上述設定的閾值(邊界值)且進化代數已大于一定的代數(本文設置為3 000),則斷定該算法對該求解問題尋優失敗; 其他參數設置同上,對比算法在每個求解問題上獨立執行30 次; 計算出SR(執行成功率,執行成功率=算法找到求解精度邊界值所需要的代數/算法總的執行代數)值和mean_iter(平均進化代數)值,對比算法的SR越大且mean_iter越小,其性能越優,表4 中符號“NA”表示對比算法尋優受挫,最好結果用加粗突出顯示.從表4 中可獲得,FPA 算法只有在2 個求解問題上的尋優成功率達到100%,其余都是0,對于函數F05,所有算法都尋優失敗,這是由于該函數的特殊屬性,使得很多群智能算法很難找到其全局極小值.TLGFPA 算法和TLFPA 算法在16 個函數上,都有11 個函數的尋優成功率是100%,但是TLGFPA 算法在這11 個函數上的平均收斂迭代次數都小于TLFPA算法,尤其在函數F01、F15、F16 上,TLGFPA 算法的平均收斂迭代次數比TLFPA 算法小1 個數量級,這說明加入“動態高斯變異”機制,能有效提高算法的收斂速度.與其余4 種算法相比,TLGFPA 算法的mean_iter和SR值明顯好于對比算法,說明TLGFPA 算法的求解速度和穩定性要優于比較算法.

由表4 可知,FPA 算法的總的平均尋優成功率只有12.5%,通過在FPA 算法中引入新的策略,TLFPA和TLGFPA 算法的尋優成功率得到大幅度提升,其中TLGFPA 算法的尋優成功率為65%,是6 種算法中最高的,說明TLGFPA 算法的穩定性最強.

表4 6 種算法的尋優成功率、平均迭代次數比較

4.1.3 Friedman 與Wilcoxon 檢驗

為了更客觀評價對比算法的綜合優化能力,本節從數學統計的角度(非參數Friedman 統計檢驗)進行對比實驗,其對比結果見表5 和表6 所示,分別是所有算法在16 個函數(維數D=30,函數F13、F14 的維數分別為4 和2)和14 個函數(維數D=100)上的Friedman的檢驗結果,從表5 和表6 可以看出,TLGFPA 算法不管在低維還是在高維上,總體性能最好,則進一步說明改進的算法是有效的.

表5 對比算法在16 個函數上的Friedman’s test (D=30,4,2)

表6 對比算法在14 個函數上的Friedman’s test (D=100)

為了更深入地對算法的優化能力進行綜合評價比較,運用a=0.05 的Wilcoxon 檢驗分析,其對比分析結果見表7 和表8,從兩個表中獲得,TLGFPA 算法與ABC,DNLPSO,TLBO 和FPA 算法之間的優化性能的差于性比較顯著,與TLFPA 顯著性差異要弱一些,但也小于0.05.這表明改進策略對提升FPA 算法的尋優性能是可行有效的.

表7 對比算法在16 個函數上的Wilcoxon’s test (D=30,4,2)

表8 對比算法在14 個函數上的Wilcoxon’s test (D=100)

4.1.4 尋優性能對比分析圖

為了更直觀地表明TLGFPA 算法的整體尋優性能優于其余對比算法,本文畫出了部分求解問題上的算法求解過程曲線圖,具體見圖1.從圖1 可知,TLGFPA算法與其他5 種對比算法相比,其優化能力明顯好于其他算法,其經過少量的進化代數就能找到理論最優值或接近理論上的最優值; 在F06 和F16 求解問題上,TLGFPA 算法和TLFPA 算法的優化能力旗鼓相當,但明顯好于其余對比算法,在F05 和F11 函數上,TLGFPA算法的求解精度要劣于ABC 算法,但比其他對比算法好; 對于函數F07,TLGFPA 算法要劣于TLBO,FPA和TLFPA 算法,但略好于其他2 種對比算法.這說明TLGFPA 的優化過程得到提速,尋優精度得到提高.

圖1 6 種算法的適應度值收斂曲線

同時,為了進一步深入地說明TLGFPA 算法在求解問題過程中的魯棒性和解的質量優于FPA 等對比算法,本文也畫出了對比算法在部分求解問題上執行30 次的優化結果變化對比圖和所有算法在求解問題上的方差對比分析圖,具體分別見圖2 和圖3.可見在這4 類函數上,TLGFPA 算法的求解精度、穩定性要好于DNLPSO,ABC,TLBO 和FPA 對比算法,而略好于TLFPA 算法.這進一步顯示改進算法在求解精度、穩定性上都得到了較好的提升.

圖2 6 種算法在部分函數上的最優適應度值比較圖

圖3 6 種算法的全局最優值方差分析

綜上所述,TLGFPA 算法的優化能力表現比較突出,驗證了本文改進算法的可行性和有效性,也證明了加入動態高斯變異的有效性.

4.2 與現有改進的FPA 算法比較

為了測試TLGFPA 算法與現有改進的FPA 算法在性能上是否具有不錯的競爭力,本節選用3 種改進的FPA 算法進行對比,分別是改進的花授粉算法(modified flower pollination algorithm,MFPA)[11]、基于廣義反向學習的改進花授粉算法(modified genera-lised oppsition-based flower pollination algorithm,MGOFPA)[11]及基于精英反向學習的花授粉算法(elite oppositionbased flower pollination algorithm,EOFPA)[7],為了更好突出本文算法的優勢,在迭代次數較少(最大迭代次數為500)的情況下比較4 種算法的尋優性能.其中,對于TLGFPA 算法除迭代次數外,其余實驗參數和求解問題同第4.1 節; 對于MFPA、MGOFPA 和EOFPA 算法的參數p取相同的值0.8、種群規模n=30 和進化代數不同于相關文獻外,其他參數取自相關文獻中,為了避免實驗的偶然性誤差,每種對比算法在其每個求解問題上都單獨執行30 次,各種對比算法的優化結果如表9所示.

從表9 可知,改進算法在所有求解問題上的優化能力明顯好于MFPA 算法; 與MGOFPA算法相比,TLGFPA算法的尋優能力在93.75%的求解問題上要優; EOFPA和TLGFPA 算法相比,TLGFPA算法在7 個求解問題上的優化能力要比EOFPA 算法優,尤其是在F02 求解問題上,TLGFPA算法能找到理論上的最優解,兩種算法在4 個求解問題(F06、F08、F14 及F15)上的優化能力旗鼓相當,而TLGFPA 算法在剩余5 個求解問題上的尋優能力要遜色于EOFPA算法.

為了更直觀地說明TLGFPA算法的優化性能好于其余對比算法,本文畫出了對比算法在部分求解問題上的收斂過程曲線圖,具體見圖4.從圖4 可看出,本文算法的求解速度在7 個函數上是4 種算法中最快的.借助表9 中“?”的數學統計結果和圖4 的收斂曲線可以看出,TLGFPA 算法的性能總體上要優于其他改進算法,顯示出較好的競爭力.

圖4 4 種改進的FPA 算法收斂曲線圖

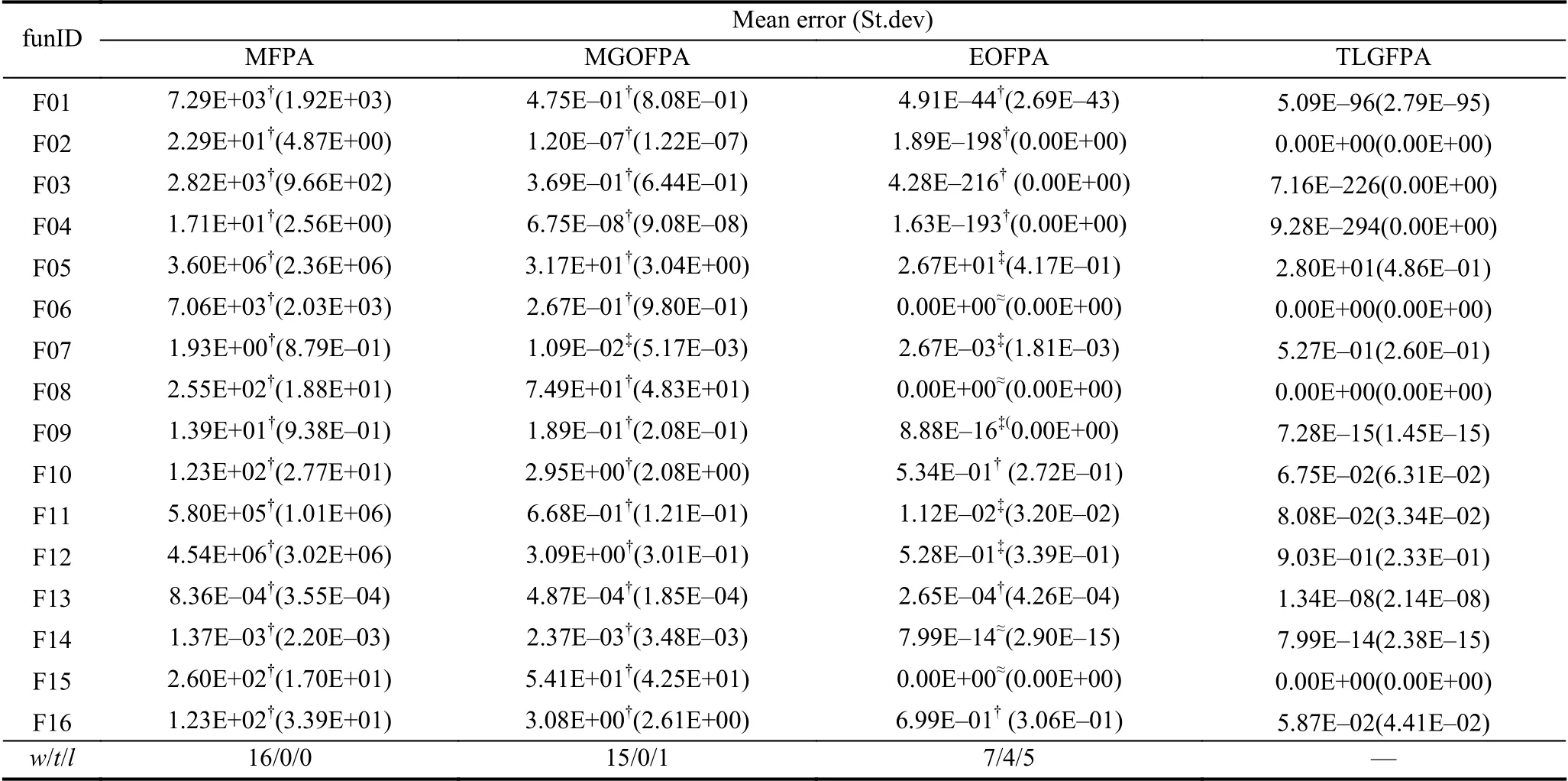
表9 4 種改進算法的尋優性能對比

4.3 利用改進算法對伸縮繩應用問題進行求解

為了驗證新算法在應用優化問題上的尋優性能,檢驗其可行性和有效性,本文選用伸縮繩應用問題進行測試.

4.3.1 伸縮繩問題的描述

在滿足x1(d)、x2(D)和x3(P)三個約束條件下使設計的繩最輕,其中d、D及P分別表示為“線的直徑”“平均卷的直徑”及“卷數”.該問題利用式(13)對其進行數學模型化,其對應的結構如圖5 所示.

圖5 伸縮繩的結構圖

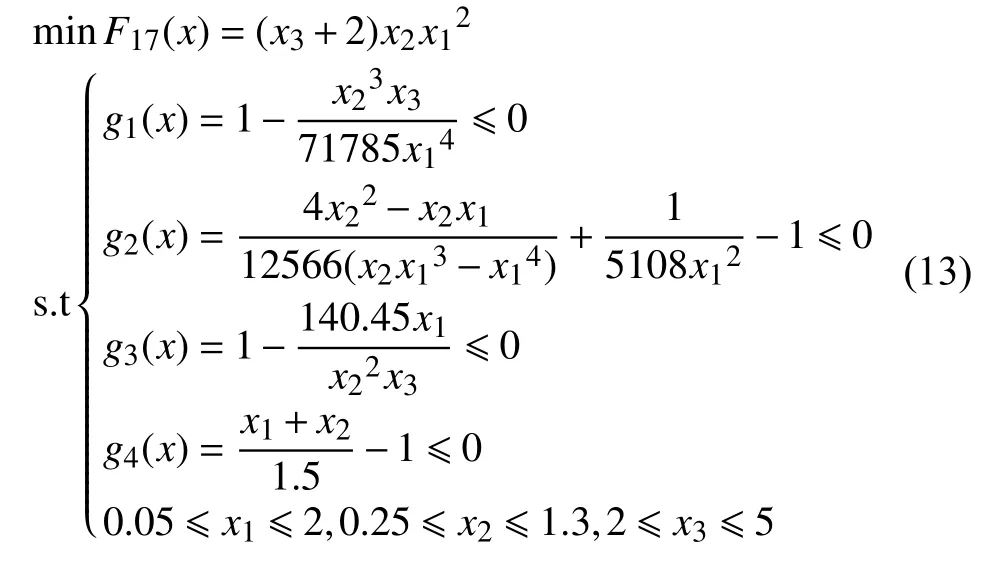
4.3.2 實驗結果及對比分析

為了進一步佐證本文算法是否行之有效,本節利用TLGFPA 算法對上述伸縮繩設計問題進行求解,并與文獻協同進化差分進化算法(co-evolutionary differential evolution,CDE)[17],一種基于可行性規則的混合粒子群約束優化(hybrid particle swarm optimization with a feasibility-based rule for constrained optimization,HPSO)[18],加速自適應權重模型(accelerating adaptive trade-off model,AATM)[19],社會和文化算法(society and civilization algorithm,SCA)[20],精英教學優化算法(elitist teaching-learning-based optimization,ETLBO)[21],

反饋精英教學優化算法(feedback elitist teachinglearning-based optimization,FETLBO)[22],基于精英反向學習的花授粉算法(elite opposition-based flower pollination algorithm,EOFPA)[7]求解結果進行比較.本節的實驗參數分別設置為: 種群規模都為25,進化代數為2 000,其余參數設置同第4.1 節,實驗結果如表10 所示.從表10 可以看出TLGFPA 算法對伸縮繩問題的優化效果要優于其他5 種算法,這表明本文的改進策略是可行和有效的.

表10 8 種算法對伸縮繩優化問題的求解結果

5 結論與展望

為了進一步解決花授粉算法的優化能力還不太理想的問題,本文提出了先對教與學優化算法中的教學因子進行改進,再把改進的教與學優化機制和動態高斯變異融入到花授粉算法中的混合算法(TLGFPA).首先,通過對16 個無約束函數的仿真實驗顯示新算法能夠較好地解決“早熟”問題,有效地提升了FPA 算法的求解精度和求解速度等性能.其次,選擇了3 種FPA改進算法進行了對比實驗,對比分析結果顯示TLGFPA算法的性能總體上要優于其他改進算法,顯示出較好的競爭力.最后,用TLGFPA 算法求解伸縮繩應用優化問題,實驗結果進一步驗證了本文算法在解決應用問題時,也比FPA 算法和其他對比算法具有更好的優化能力.

雖然本文算法性能還不錯,但在解決大規模優化問題時,其優化能力還有待提高,后續將針對此問題進一步研究.在今后的研究工作中,可以嘗試利用改進差分進化算法的思路來對其局部搜索部分進行改進,增強其開發能力.因為其局部搜索部分是采用了傳統差分進化算法的思想,在優化復雜多維的優化問題時,性能較差.同時,將其應用領域進一步地進行推廣,如解決動態組合優化問題.其次,目前“二進制的花授粉算法”研究很少,如何將二進制的花授粉算法運用到軟件工程、大數據、量子計算等領域將是值得研究的問題.