基于層次密度聚類的去噪自適應混合采樣①
姜新盈,王舒梵,嚴 濤
(上海工程技術大學 數理與統計學院,上海 201620)
現實中的很多領域存在的數據集都是不平衡的,這類數據集有著不同類別數據樣本不均、數量相差較大的特點,其中大多數樣本的類別稱為多數類別,其余樣本的類別稱為少數類別.由于不平衡數據的廣泛存在,從不平衡數據中學習對于研究界及現實應用都至關重要,例如疾病診斷[1]和石油儲層含油量識別[2]等.任何分類器的目標都是最大程度地提高總體準確性,但是傳統分類器往往更傾向于多數類樣本,這就導致少數類樣本分類錯誤[3].實際應用中,從不平衡數據中學習到的分類器需要同時在不同類別樣本上均表現良好,因此在保證多數類別分類精度的前提下,如何處理不平衡數據以提高少數類別分類準確性.
1 引言
現有的一些廣泛處理不平衡數據分類的方法主要分為數據預處理、算法改進及特征選擇這3 個層面,當前沒有一種方法能夠很好地解決所有不平衡數據集分類問題,算法改進僅僅針對單一的分類器進行改進,特征選擇容易造成信息丟失,但是數據層面的抽樣方法顯示了巨大的優越性,該方法主要是改善數據集本身而不是分類器.
欠采樣是對多數類樣本進行處理,選擇一些多數類樣本進行剔除以提高少數類樣本的分類正確率.Yen等[4]提出SBC 算法,首先將整個數據集聚類,再根據每簇采樣數量進行欠采樣,但是容易丟失關鍵信息.過采樣是通過合成少數類樣本以增加少數類樣本的算法,Barua 等[5]提出MWMOTE 算法,先選擇少數類樣本的適當子集,根據不同類別樣本間的距離對少數類樣本分配權重,再使用聚類方法并結合SMOTE 算法合成新的少數類樣本; Nekooeimehr 等[6]提出自適應半無監督加權過采樣,先對少數類樣本進行分層聚類,并根據分類復雜度等自適應地對每個子集中靠近邊界的少數類樣本進行過采樣,避免生成與多數類重疊的合成少數類樣本.石洪波等[7]研究表明使用單一的采樣算法或導致過擬合或誤刪重要樣本,而文獻[8]表明混合采樣的分類性能比單個采樣算法好,在提高運行效率,有效避免過擬合問題的情況下,還不易丟失含有重要信息的多數類樣本.戴翔等[9]提出BCS-SK 算法,采用SMOTE 合成少數類樣本,然后采用K-means 聚類算法對多數類樣本進行欠采樣;史明華[10]對整個數據集進行聚類,根據每簇不平衡率的大小將數據集分為4 類并采取不同的采樣方法,均衡了簇內的樣本分布.
以上算法各具優勢,但大部分沒有解決類內小分離及易合成低質量樣本的問題,也沒有區分不同樣本的重要性,為解決以上問題,本文提出了基于層次密度聚類的去噪自適應混合采樣算法(adaptive denoising hybrid sampling algorithm based on hierarchical density clustering,ADHSBHD)來有效合成高質量樣本.
2 相關理論
2.1 HDBSCAN 聚類
HDBSCAN 聚類算法[11]是McInnes 等人研究提出的一種基于層次聚類的最新算法,是對DBSCAN 密度聚類算法的優化,能處理不同密度和任意形狀的聚類[12],一方面是不再將Eps值作為樹狀圖的切割線,而是通過查看分裂來壓縮樹狀圖,使用該樹選擇最穩定的簇,并以不同的高度來切割樹,這樣可以根據簇的穩定性選擇密度不同的簇; 另一方面是不再需要人工設置Eps參數,只需要設置集群最小樣本數量min_samples來確定樣本是離群點還是分裂為兩個新集群即可.
相比于K-means、DBSCAN 等常用聚類具有對參數設置不敏感的優勢,通常設置兩個參數: 最小集群數量min_cluster_size,集群最小樣本數量min_samples.此外,HDBSCAN 具有噪聲感知能力,-1 表示該樣本點不在任何簇內,并且聚類結果會給數據集中的每個樣本都賦予一個0.0-1.0 的概率值,用于代表屬于某個簇的可能性,概率值為0.0 則表示該樣本點不在集群中(所有的離群點都是這個值),概率值為1.0 則表示該樣本點位于簇的核心.
2.2 Random-SMOTE 算法
由于SMOTE 算法存在合成樣本區域有限、易產生噪聲等問題,董燕杰[13]提出Random-SMOTE 算法,可以提高算法效率并更符合原數據集樣本空間.該算法的核心思想是根據3 個樣本點構成三角區域,在區域內生成新樣本,首先從少數類數據集中選擇樣本x作為根樣本,并且隨機選擇y1、y2這兩個樣本作為間接樣本,根據式(1)在y1、y2間線性插值,根據設置的采樣倍率N,生成N個臨時樣本pj,j=1,2,···,N.

其次根據式(2)在pj和x之間線性插值得到新樣本mj.

3 ADHSBHD 算法
文獻[6]表明,聚類是不錯的解決類內不平衡及小分離問題的方法.為了更深入研究解決噪聲、類內不平衡和小分離問題,提出了基于層次密度聚類的去噪自適應混合采樣算法(ADHSBHD).
3.1 基于HDBSCAN 的去噪方法
在很多情形之下,噪聲樣本會使分類器性能損失,聚類作為潛在的噪聲檢測算法,為識別噪聲提供了另一研究思路.為了有效識別噪聲點,提出了一種基于HDBSCAN 的去噪方法,首先對少數類樣本集中的每個樣本計算其k近鄰,若該樣本k近鄰全部是多數類樣本,則把該樣本點視為全局離群點.然后引入HDBSCAN聚類,將少數類樣本集進行聚類,得到若干個簇,將概率值為0 的樣本視為局部離群點,取全部離群點集和局部離群點集的交集為噪聲集,這樣可以較全面地識別出噪聲點,也避免直接刪除處于小分離狀態的樣本,為接下來提出的ADHSBHD 算法在安全區域內生成樣本做準備.
3.2 對少數類樣本的處理
若每個簇內都合成同樣數量的樣本,那么容易造成類重疊,也無益于類內不平衡的解決,因此,在對少數類樣本聚類并去除噪聲之后,需要根據每簇的密集稀疏程度,確定每個簇所需合成的樣本數量,分配給每個簇一個0 到1 的采樣權重,這樣可以使稀疏區域的樣本增添有益信息,密集區域的樣本盡可能地減少類重疊,不會忽略對小規模集群的學習.為了表示每簇的密集稀疏程度,用平均距離來表示.
定義1 (平均距離).對于數據集C和少數類樣本的任意簇C(1k),1 ≤k≤m,簇C(1k)的平均距離記為Meandist(C(1k)),即:

其中,dij為簇內各樣本之間的歐式距離,n為簇內樣本數量.
定義2 (采樣權重).任意簇C(1k),1 ≤k≤m的采樣權重為某簇的平均距離與所有簇的平均距離之和的比值,即:

當各簇的平均距離越小時,說明簇內樣本更密集,反之,則更稀疏.相應的,簇內樣本越密集時,需要合成的樣本越少,即采樣權重就越小,反之,需要合成的樣本就越多.
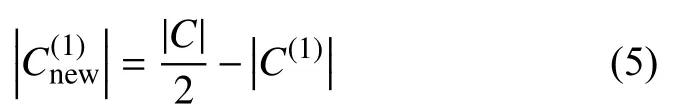
其中,|C|表示原始數據集C的樣本數量,表示少數類樣本的個數.
每簇C(1k),1 ≤k≤m需要合成的樣本數量定義如下:
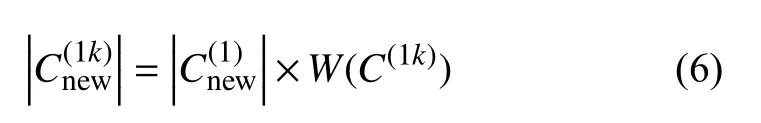
3.3 對多數類樣本的處理
根據HDBSCAN 對多數類樣本聚類,得到若干個簇和離群點,相應的得到每個簇的概率值矩陣,當概率值較低時說明樣本點越在簇的邊緣,過多的邊緣樣本會使分類器發生偏向而降低少數類的分類精度.為此,將所有多數類樣本的概率值按照從小到大的順序排列,按照一定規則,刪減的多數類樣本數量定義如下:

3.4 ADHSBHD 算法流程
ADHSBHD 算法的具體步驟描述如算法1.

算法1.ADHSBHD 算法輸入: 原始數據集 ,近鄰參數,最小集群數量min_cluster_size,集群最小樣本數量min_samples Cnew C k輸出: 均衡數據集C(0)C(1)C=C(0)∪C(1)C(0)∪C(1)=? Step 1.將原始數據集劃分為多數類樣本集和少數類樣本集且且,并識別噪聲.C(1)xkk Nt Step 1.1.計算中各個樣本,計算其近鄰,若近鄰均為多數類樣本,則將該添加到全局離群點集 中.C(1)m C(11),C(12),C(13),···,C(1m)pij,0<i≤m,0<j≤■■■C(1i)■■■NlN=Nt∩NlC NC′■■■■C′■■■■=|C|-|N|Step 1.2.用HDBSCAN 對聚類,得到 個相互獨立且不同規模的簇和若干個離群點,并且得到每個簇的樣本概率值矩陣,而離群點的概率值為0,將其添加到局部離群點集 中,則噪聲集群.從原始數據集 中刪去噪聲集群 ,得到 ,其樣本量.for i=1 to■■■C(1i)■■■Step 2.,計算每個簇需要合成的新的樣本數量并自適應合成.Step 2.1.計算每個簇中樣本之間的歐氏距離,并得到各簇的平均距離.Meandist(C(1k))W(C(1k))Step 2.2.計算每簇的采樣權重.■■■■C(1k)new■■■■x Step 2.3.計算每簇新的樣本數量,并選中簇內樣本做目標樣本,從它的近鄰中隨機選擇兩個樣本 、 ,先通過 、 隨機生成一個輔助樣本,再在目標樣本和輔助樣本之間線性插值隨機生成新樣本,即采用Random-SMOTE 在三角形區域內隨機合成樣本,將合成樣本添加到中,直到新樣本數量為.k y1y2y1y2 a x a C(1k)new■■■■C(1k)new■■■■C(1k)C(1k)new Step 2.4.合并每簇的與,各簇原始的少數類樣本集與合成樣本組成新的數據集中.C(1)new C(0)Step 3.對多數類樣本進行處理.C(0)n C(01),C(02),C(03),···,C(0n) t pij,0<i≤n,0<j≤■■■C(0i)■■■Step 3.1.對用HDBSCAN 聚類,得到個相互獨立且不同規模的簇和個離群點,并且得到每個簇的樣本概率值矩陣.t<■■■C(0)■■■-|C|2C(0)Step 3.2.當時,將中的樣本按照概率值從小到大排序,刪去離群點和部分概率值小的點,共個樣本; 當時,對刪除個離群點,剩余的多數類樣本添加到新的數據集中.Cnew=C(0)new∪C(1)new Step 4.并對分類器進行訓練.■■■C(0)■■■-|C|■■■C(0)■■■-|C|2 t≥■■■C(0)■■■-|C|2 C(0)2 C(0)new
4 實驗結果與分析
4.1 評價指標
準確率作為分類器評價指標對于非平衡數據有失公平,為了客觀評價分類算法性能好壞,研究學者常常根據混淆矩陣引入的概念來評估算法性能.根據表1的混淆矩陣,引入查全率(Recall)、查準率(Precision)、F-value值、G-mean值、AUC等定義.

表1 混淆矩陣
各定義的公式如下:

此外,AUC作為可視化指標,是根據引入的ROC曲線下的面積來表示,值越大,說明分類器性能越好.ROC曲線則是以真正例率為縱軸,以假正例率為橫軸繪制的.
4.2 數據集描述
為了驗證ADHSBHD 的有效性,本文從國際機器學習標準庫UCI 中選取了Ionosphere、Glass、Abalone、Haberman、Vehicle、Ecoli、Yeast 這7 組不平衡數據集,其中,Glass 的少數類特征為“1”; Abalone 的少數類特征為“F”; Vehicle 數據集中,將第一類視為少數類;Ecoli 的少數類特征為 “om”“omL”和“pp”; Yeast 數據集中將“MIT”視為少數類.7 組數據集的具體信息如表2所示.

表2 數據集信息
4.3 實驗分析
為了驗證本節所提出的ADHSBHD 算法表現良好,ADHSBHD 算法分別與SMOTE 算法、ADASYN算法、Random-SMOTE 算法(以下簡稱R-SMOTE)、SVMSOMTE 算法在這7 組數據集上做重采樣的對比實驗,用F-value、G-mean、AUC作為評價指標,實驗環境均在Jupyter Notebook 中運行,所使用的對比算法除R-SMOTE 外均調用imbalanced-learn 程序包實現.
此外,SVM 中核函數為高斯核函數,其他超參數均為imbalanced-learn 中的默認值,為了直觀驗證上述各對比采樣算法的有效性,設置k=5,相應的算法中的其他超參數也均為默認值,而ADHSBHD 算法中使用到的HDBSCAN 算法設置最小集群數量min_cluster_size=2,集群最小樣本數量min_samples=4.
表3、表4 和表5 展示了7 組數據集6 種不同采樣算法下的F-value值、G-mean值和AUC值以此來衡量算法分類結果,黑體加粗的數值表示同一數據集的最優算法對應指標值,avg 表示不同數據集在不同組合形式的算法下的平均值.從各表中可以看出,雖然對Haberman 數據集使用Random-SMOTE 算法的結果優于本文算法結果,這是由于本文在引入聚類算法后,在如何選擇最佳樣本參與合成時存在不足,而Random-SMOTE 算法的合成方法更符合Haberman 數據集.但是從整體性能上看,ADHSBHD 算法應用到SVM 分類器后提升了整體分類精度,在F-value、G-mean、AUC這幾種性能指標方面均優于文中所提其他4 種對比算法.

表3 不同數據集在支持向量機下的F-value 性能對比
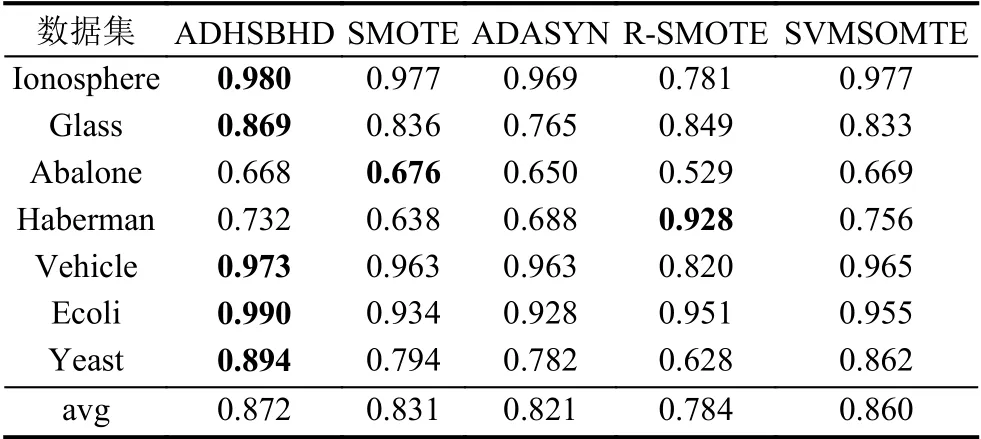
表4 不同數據集在支持向量機下的G-mean 性能對比
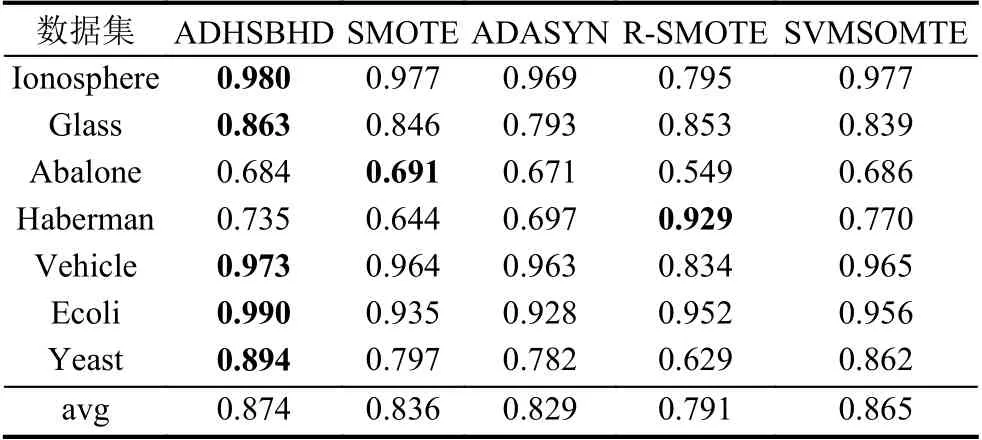
表5 不同數據集在支持向量機下的AUC 性能對比
5 結論
本文提出了基于層次密度聚類的去噪自適應混合采樣算法(ADHSBHD),以層次密度聚類為基礎,考慮到不同類別樣本的樣本空間分布,為了驗證ADHSBHD的有效性及穩定性,將該算法與SVM 分類器結合在一起,并與4 種采樣算法進行實驗對比,實驗結果表明,該算法與不同的分類器的組合有較好的泛化性,Fvalue、G-mean、AUC這3 個評價指標在上述大部分數據集上都有所提升.由于該算法是基于聚類算法展開,后續可以研究其他的聚類技術能否為該算法帶來更高性能.

