永磁同步電機超螺旋滑模自抗擾調速系統設計

杜海明，高 函，胡智宏，申永鵬，范明杰

(鄭州輕工業大學 電氣信息工程學院, 鄭州 450002)

0 引言

永磁同步電機因具有密度高、效率高和損耗小等優點，在電機應用領域備受關注[1-2]。為提高永磁同步電機的調速性能，基于調速系統采用多種非線性控制方法，如模型參考自適應、滑模控制、模型預測控制等[3-4]，但都存在計算量大和依賴精確數學模型等缺點。孫斌等[5]提出的自抗擾控制方法是一種不依賴于精確數學模型、具有較強調節能力和抗擾性的非線性魯棒控制方法，但存在參數調節復雜的缺點。為減少參數調節，文獻[6]將快速最優控制綜合函數換成常數的線性自抗擾控制器，但降低了系統的快速性；將分數階PID控制和自抗擾控制相結合，設計模糊控制器用于簡化參數整定，但模糊規則難于建立[7]。分數階自抗擾控制器在魯棒性和快速性方面具有優勢，但存在算法復雜度高、較多可調參數問題[8]。

滑模控制由于同系統參數和擾動無關，具有魯棒性強和快速性好的優點，但存在一定的抖振[9]。為降低系統的抖振，文獻[10]采用一種新型滑模趨近律，但帶來了計算復雜度高的問題。基于傳統滑模理論，高階滑模通過將不連續的控制量作用在高階導數上，能夠有效減少系統的抖振，但存在滑模變量的導數信息難以獲取的問題[11]。超螺旋滑模是基于高階滑模理論發展起來的二階滑模變結構控制方案，它不僅具有高階滑模抑制抖振的優點，同時不需要獲取滑模變量的導數信息[12-13]。文獻[14-16]將超螺旋滑模控制應用于電機控制系統中，有較快的系統響應速度，同時提升了系統的魯棒性，但與自抗擾控制策略相比，超螺旋滑模控制策略更依賴精確的數學模型。

基于文獻[16]提出的永磁同步電機SVM-DTC控制系統方案，本研究對其速度環控制器進行改進，提出了STSM-ADRC控制策略。新控制策略結合超螺旋滑模和自抗擾控制器的特點，將超螺旋滑模算法引入自抗擾控制中，對跟蹤微分器和非線性誤差反饋控制率進行優化，以達到減少可調參數、提高系統響應速度的目的。仿真結果驗證了所提算法的有效性。

1 數學模型

1.1 永磁同步電機數學模型

以表貼式永磁同步電機為研究對象，忽略磁滯和渦流損耗，忽略電機鐵芯飽和，建立基于d-q軸的永磁同步電機數學模型，表達式為：

(1)

(2)

式中；ud、uq為定子d-q軸電壓矢量;id、iq為定子d-q軸電流矢量；R為定子電阻，Ld、Lq為定子d-q軸電感；ωe、ωm為電角速度和機械角速度；Te、TL為電磁轉矩和負載轉矩；pn為極對數；J為電機的實際轉動慣量；B為阻尼黏滯系數。

根據式(2)可以得到PMSM速度數學模型為

(3)

(4)

式中：b0=1/J0，J0表示仿真模型中的轉動慣量；f表示總擾動。

1.2 線性自抗擾控制器數學模型

自抗擾控制是為解決PI控制器存在的超調性和快速性之間的矛盾而提出的新型控制器。但是非線性自抗擾控制器存在參數過多的缺點，因此有學者提出了線性自抗擾控制。線性自抗擾控制器主要有3部分組成：線性跟蹤微分器(LTD)，線性擴張狀態觀測器(LESO)和線性誤差反饋控制率(LSEF)。線性自抗擾控制系統的一種基本結構見圖1。

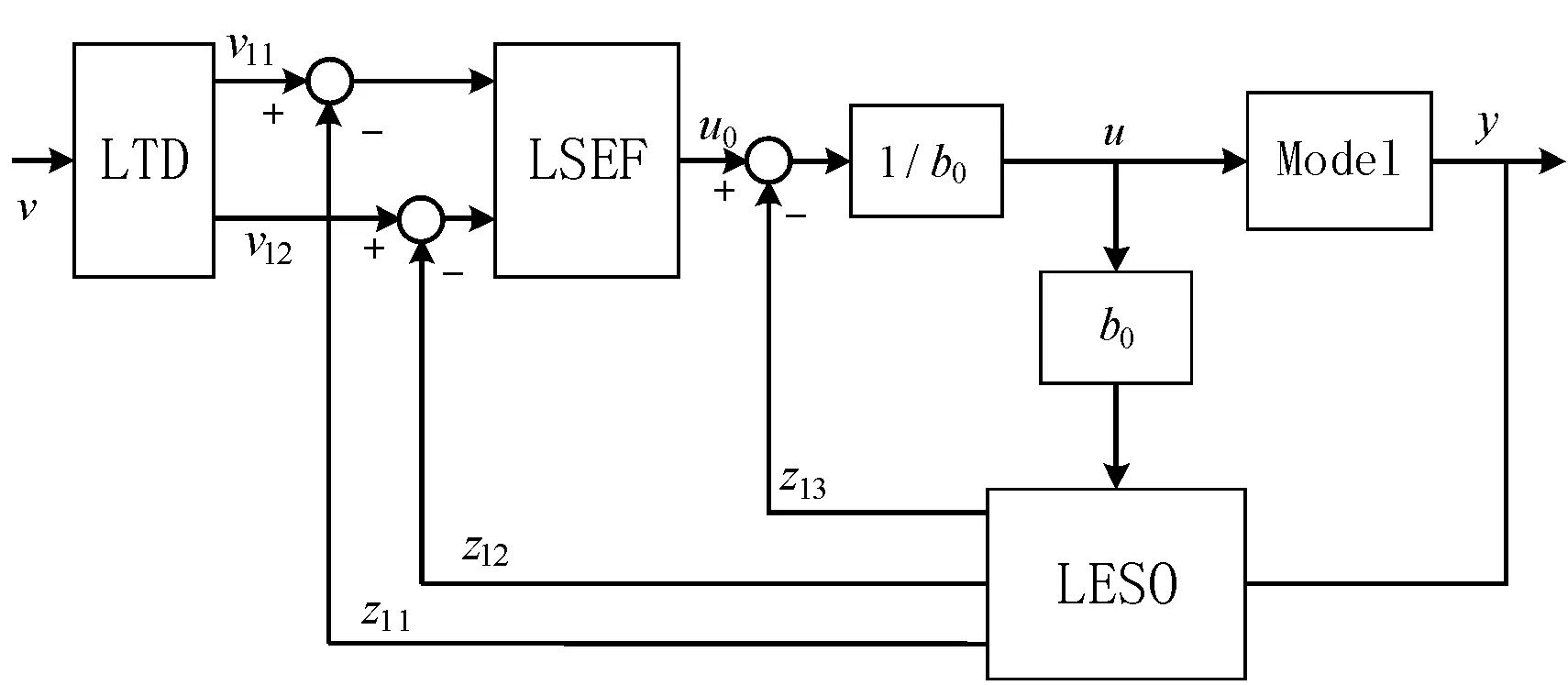
圖1 線性自抗擾控制系統基本結構框圖

圖1中，LTD的作用是對信號進行微分跟蹤，減小階躍信號導致的超調問題；LESO將總擾動擴張成新的狀態變量，并對系統進行估計和補償；LSEF將LTD和LESO的輸出信號進行非線性組合。LADRC系統的數學模型可表示為：

1) 線性跟蹤微分器(LTD)

(5)

2) 線性擴張狀態觀測器(LESO)

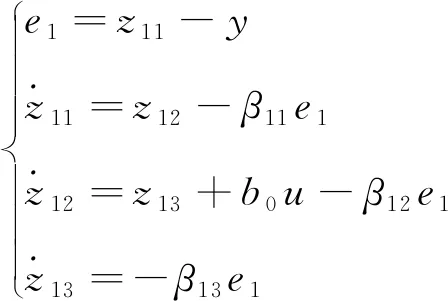
(6)

3) 線性反饋誤差跟蹤率(LSEF)

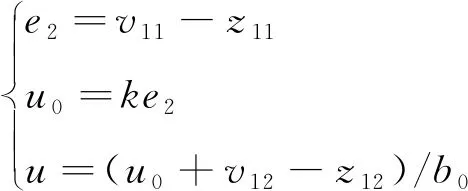
(7)

式中：e、v*、y分別為誤差信號、輸入信號、輸出信號；v11、z11、z12分別為LTD的跟蹤信號、輸出的跟蹤信號、擾動觀測值；r、β、b0、k分別為速度因子、矯正增益、補償因子、調節器增益。

2 超螺旋滑模自抗擾速度控制器設計

2.1 超螺旋滑模算法

線性自抗擾控制器雖然相對于非線性自抗擾控制器減少了可調參數，但是降低了系統的響應速度。超螺旋滑模算法是二階滑模算法的一種，它能使系統的運動軌跡以旋轉的方式在有限時間內收斂到原點，相對于傳統的滑模控制具有無抖振、快速性高的優點。因此，引入超螺旋滑模算法改善自抗擾控制器的系統性能。設動態系統結構表達式為

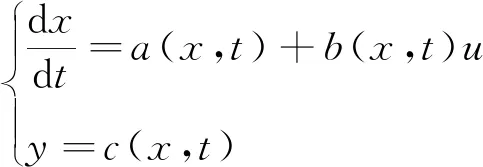
(8)

式中:x是狀態變量；u是輸入量，a、b、c是關于x的函數；y是關于x的輸出量。

設滑模變量s=y-y*，則超螺旋滑模控制器表示為

(9)

式中:kp、ki是超螺旋滑模控制器的待設計參數且大于零;r為待設計系數，一般取r=0.5。

2.2 超螺旋滑模跟蹤微分器

在線性自抗擾控制器中,二階線性跟蹤微分器的使用降低了系統的響應速度。為了提高系統的快速性，在線性自抗擾控制系統的跟蹤微分器引入超螺旋滑模算法。定義速度誤差的滑模面函數為

e0=v11-v*

(10)

式中:e0表示給定速度信號與其跟蹤信號的誤差;v11為安排過渡過程后的參考速度信號。

再令

(11)

結合式(9)(10)和式(11)得到超螺旋滑模跟蹤微分器為

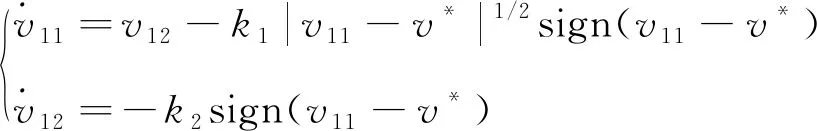
(12)

式中，v*的二階微分信號有界為M[17]，聯合式(10)(11)和式(12)得到

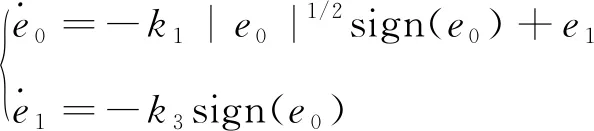
(13)

式中：k3考慮了參考速度的二階微分信號帶來的擾動，k2-M≤k3≤k2+M。采用李雅普諾夫穩定性判據進行穩定性證明，定義李雅普諾夫函數為

(14)

因此式(14)的導數為

e1(-k3sign(e0))=

-k3k1sign(e0)|e0|1/2sign(e0)<0

(15)

2.3 超螺旋滑模狀態誤差反饋控制率

由式(7)可知，線性狀態誤差反饋控制率在線性自抗擾控制器中相當于一個PID控制器中的P控制器，過大的偏差會使系統穩定性下降，降低系統的魯棒性，因此引入超螺旋滑模算法提高系統的魯棒性，取控制量為

(16)

定義誤差的滑模面函數為

(17)

式中：e2為永磁同步電機的轉速跟蹤誤差信號。

結合式(9)(16)和式(17)，利用超螺旋滑模算法的二階滑模控制基本原理得到

(18)

即超螺旋滑模狀態誤差反饋控制率為

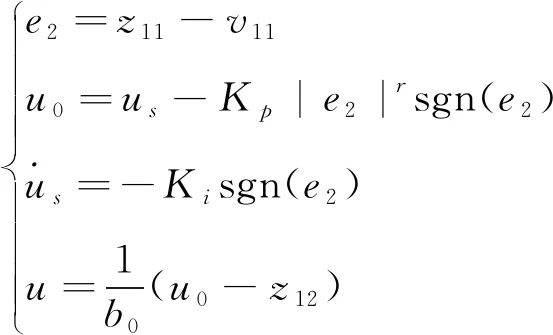
(19)

同樣，定義李雅普諾夫函數為

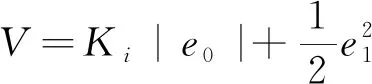
(20)

聯合式(17)(19)(20)，得到式(20)的導數為

e21(-Kisgn(e2))=-KpKi|e2|1/2<0

(21)

2.4 線性擴張狀態觀測器

將式(4)總擾動擴張為新的狀態，聯合式(6)得到線性擴張狀態觀測器為

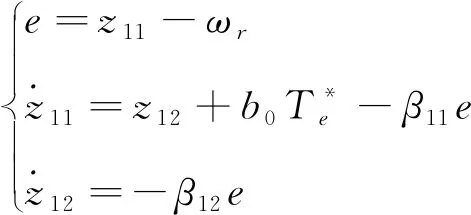
(22)

最終，STSM-ADRC速度控制器結構如圖2所示。

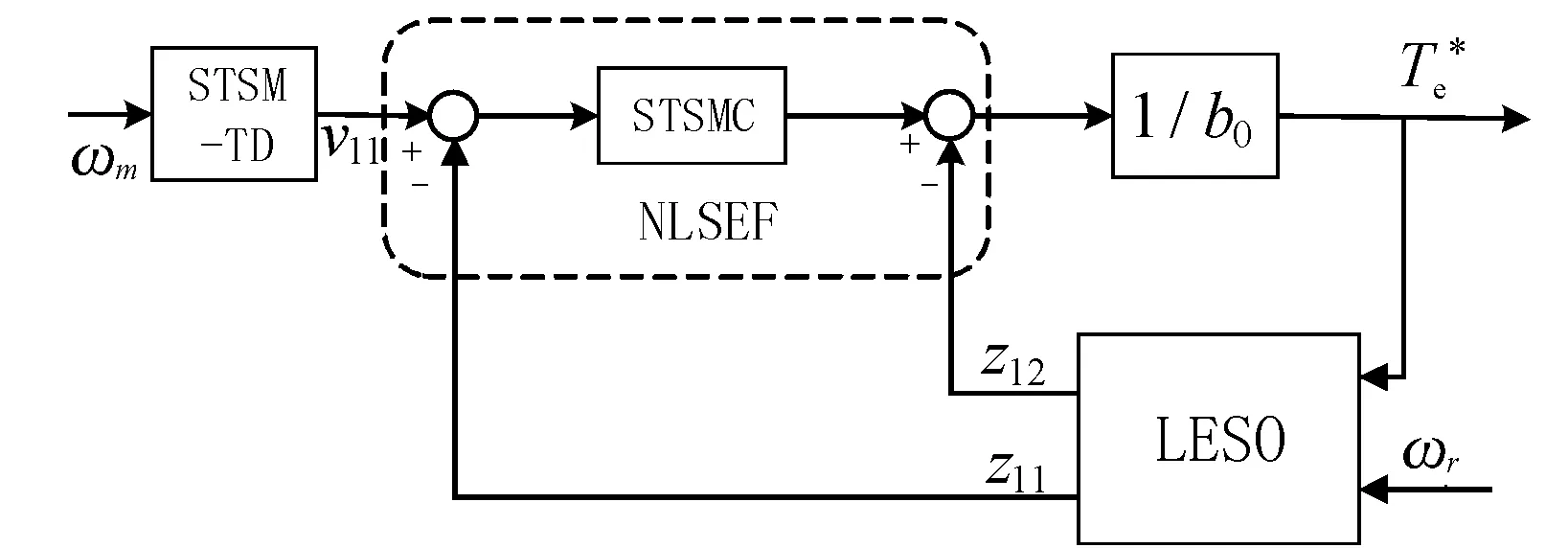
圖2 超螺旋滑模自抗擾速度控制器結構框圖

3 仿真對比分析

基于Matlab/Simulink進行仿真,驗證在PMSM上設計的STSM-ADRC控制方法的可行性和有效性。永磁同步電機參數見表1。

表1 永磁同步電機參數

基于超螺旋滑模自抗擾速度控制器的SVM-DTC結構如圖3所示。

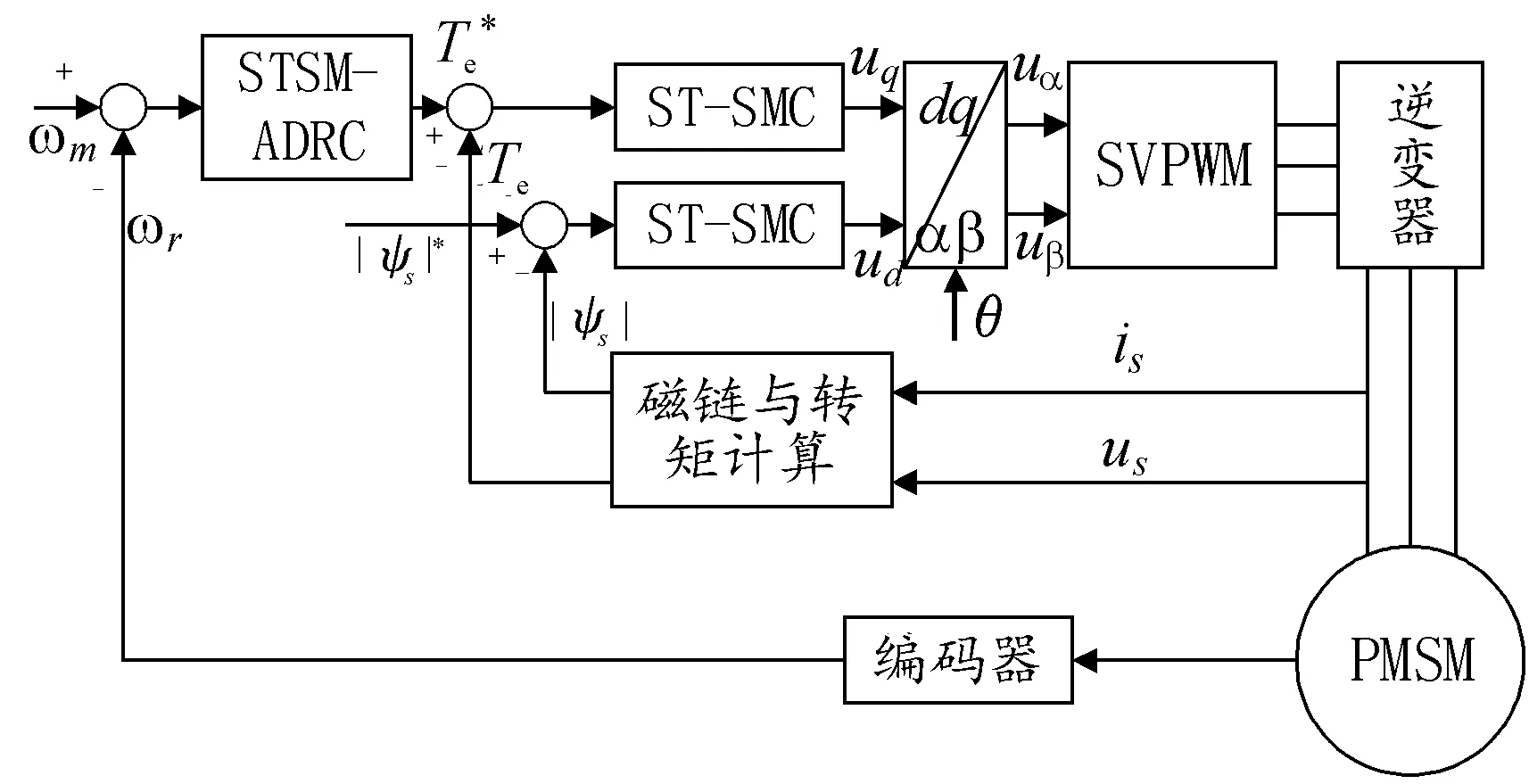
圖3 基于STSM-ADRC的SVM-DTC結構框圖

為驗證電機STSM-ADRC控制算法的速度響應性能，首先對永磁同步電機進行空載啟動實驗，仿真時間設置為0.25 s，期望轉速設置為600 r/min，結果如圖4所示。然后，對永磁同步電機進行空載變速響應實驗，仿真時間設置為0.5 s，期望轉速首先設置為600 r/min,在0.25 s時轉速設置為500 r/min，結果如圖5所示。表2和表3給出了圖4與圖5的動態性能對比數據。

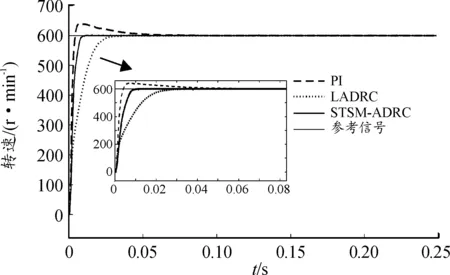
圖4 空載啟動速度響應曲線

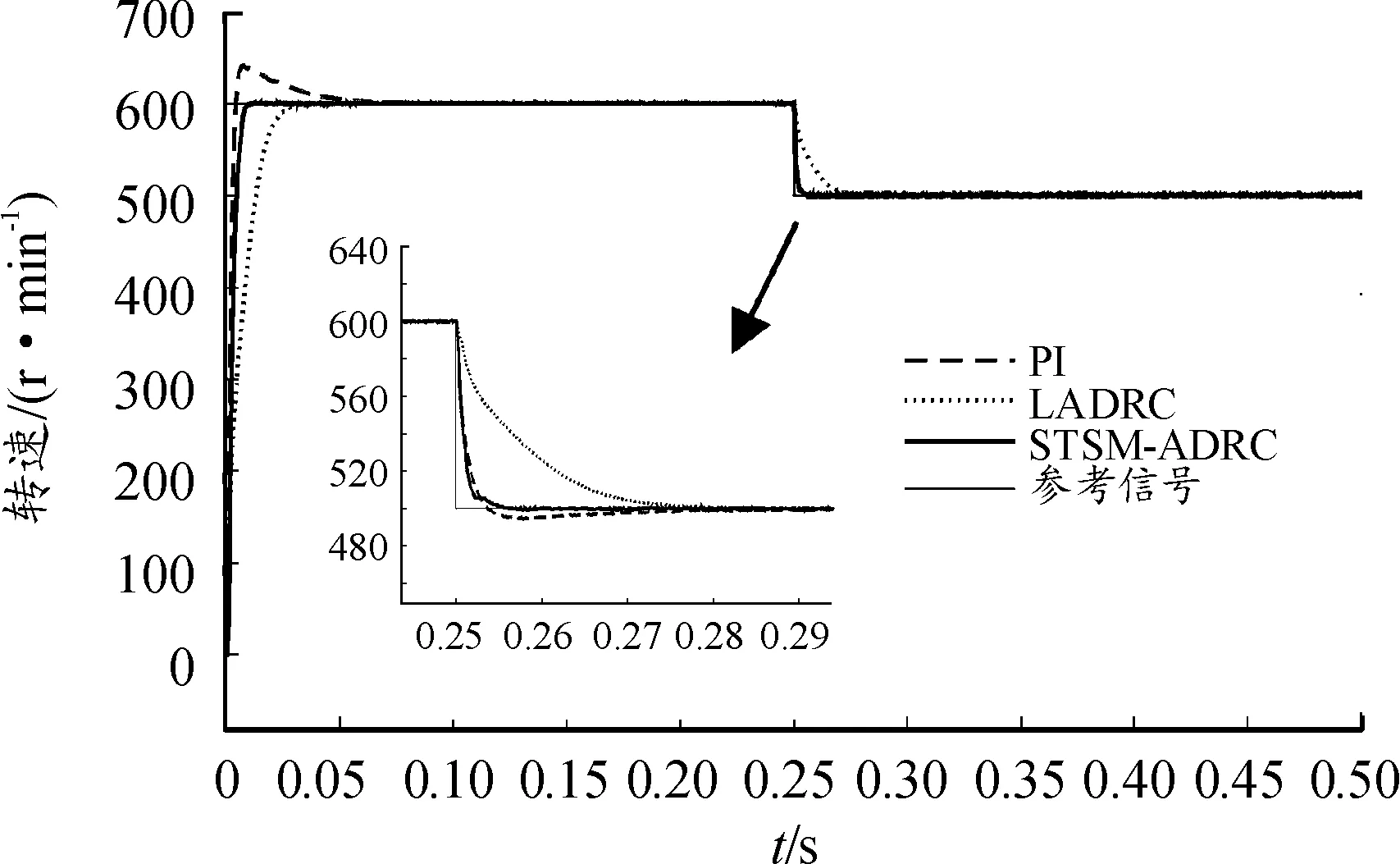
圖5 變速情況下速度響應曲線

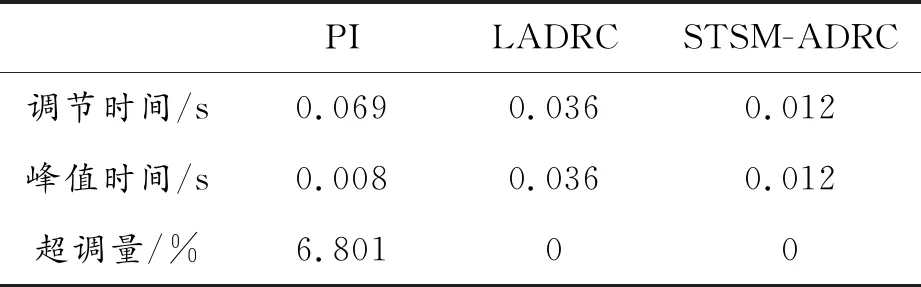
表2 空載動態性能數據

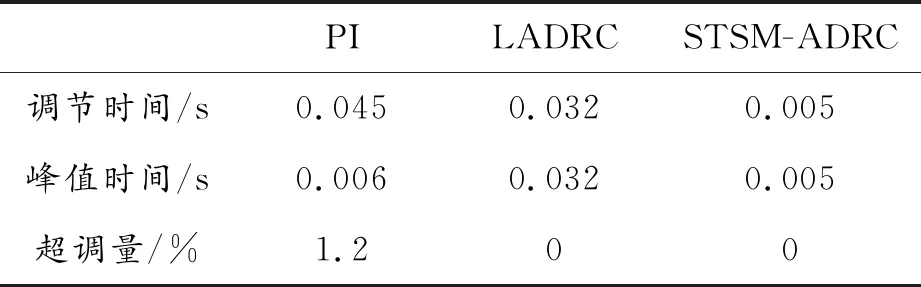
表3 變速動態性能數據

分析圖4和表2可以發現，PI和LADRC控制器所需穩定時間較長，STSM-ADRC控制器所需穩定時間最短；PI控制器到達峰值所需時間最短，STSM-ADRC控制器次之，這是因為PI控制器相較于LADRC和STSM-ADRC控制器發生了超調且首先到達峰值，而LADRC和STSM-ADRC控制器無超調，因此STSM-ADRC控制器有更快的響應速度。

分析圖5和表3可以發現，在變速干擾情況下，相對于PI和LADRC控制器，STSM-ADRC控制器所需穩定時間與到達峰值時間最小，且沒有發生超調，因此STSM-ADRC控制器可以更快地達到穩定。

為驗證所提控制策略的抗擾動能力，對永磁同步電機進行突加負載實驗，仿真時間設置為1 s，參考速度為600 r/min，在0.5 s時突加5 N的負載轉矩，其速度響應和轉矩響應如圖6和圖7所示。

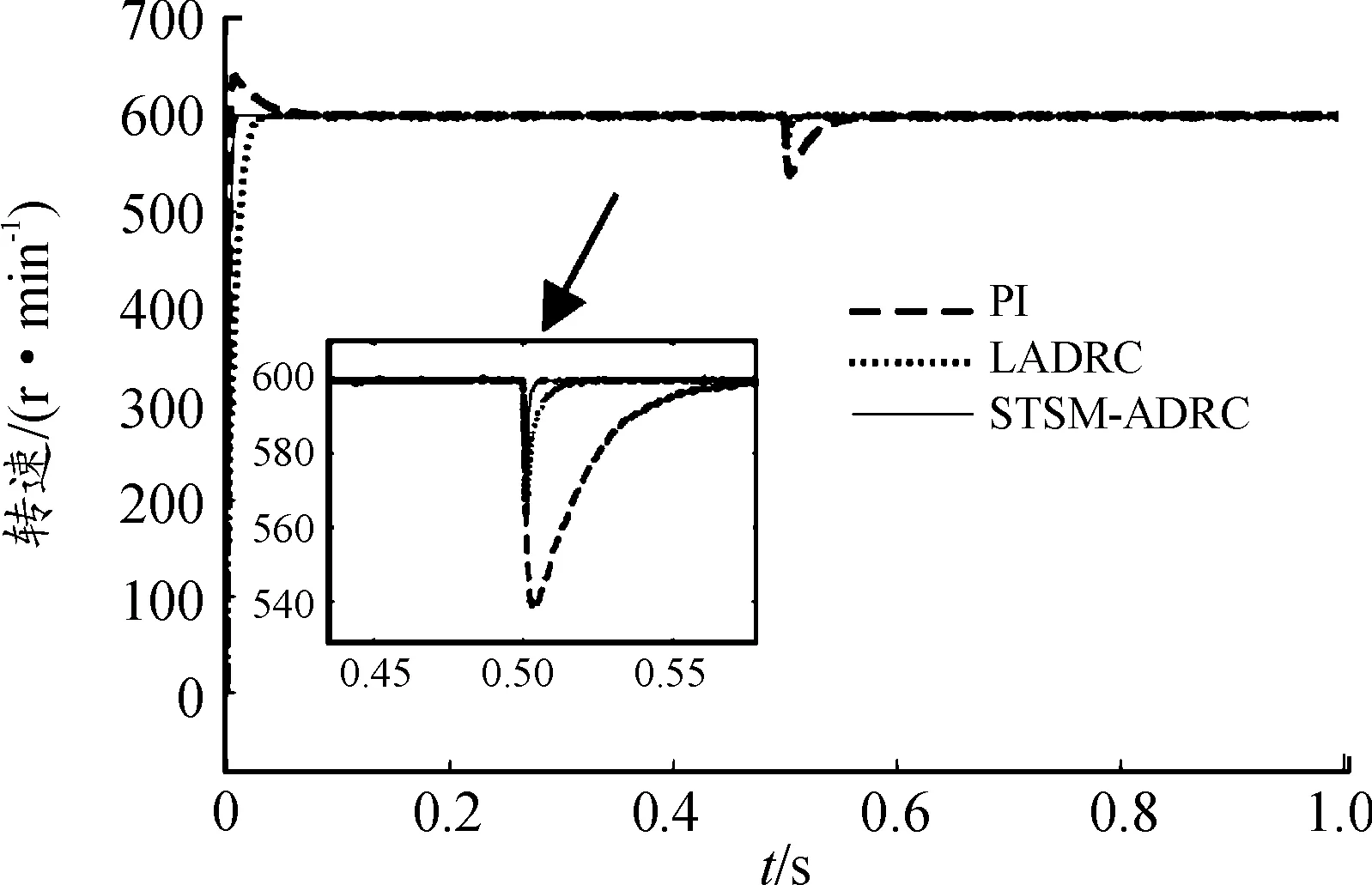
圖6 負載擾動下速度響應曲線

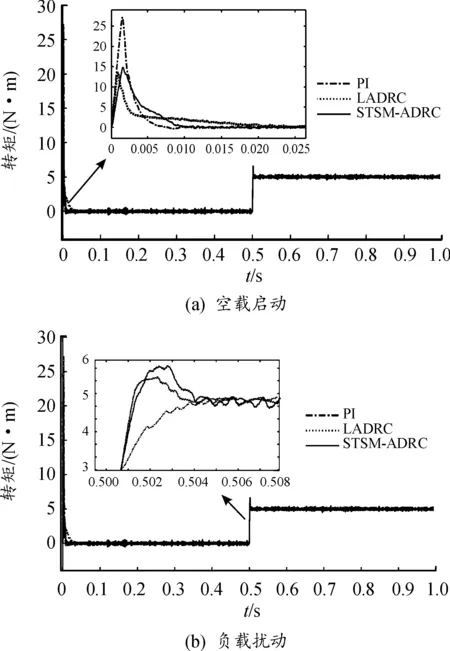
圖7 PMSM轉矩響應曲線

從圖6中可以看到，在5 N的負載擾動下，PI控制器速度波動達到62 r/min，穩定時間為0.08 s，LADRC控制器速度波動為46 r/min，穩定時間為0.015 s；STSM-ADRC控制器速度波動為34 r/min，穩定時間為0.006 s，因此在突加負載擾動情況下，STSM-ADRC控制器有更好的抗擾動能力。

為了更清楚地描述3種控制器的的轉矩響應性能，表4給出了圖7的轉矩響應性能數據。

表4 轉矩響應性能

從圖7(a)與表4中可以得出，電機在空載啟動時，3種控制方式中PI控制器啟動轉矩峰值最大，但轉矩穩定時間最短；LADRC控制器轉矩峰值最小，但是穩定時間相對較長；STSM-ADRC控制器轉矩峰值較小，穩定時間和PI控制器基本一致，表明STSM-ADRC控制器具有較好的空載啟動性能。

從圖7(b)與表4中可以得出，在突加負載情況下，3種控制器中PI控制器雖然轉矩超調較小，但是穩定時間最長；LADRC控制器轉矩超調相對較小，但是穩定時間較長；STSM-ADRC控制器轉矩超調最大，但是穩定所需時間最短，這也符合負載擾動情況下速度曲線與轉矩曲線的一致性。因此，在負載擾動下STSM-ADRC控制器具有更快的轉矩響應。

此外，為驗證所提控制策略的帶負載啟動能力，仿真時間設置為0.05 s，施加10 N的負載進行帶負載啟動。圖8為帶負載啟動時速度響應曲線。

圖8 帶負載啟動速度響應曲線

分析圖8可以得出，3種控制策略均可以實現無超調，PI控制器到達參考速度所需時間為0.07 s，LADRC控制器到達參考速度所需時間為0.035 s，STSM-ADRC控制器到達參考速度所需時間為0.012 s。因此與PI控制器和LADRC控制器相比，STSM-ADRC控制策略可以更快地達到穩態，體現了更強的魯棒性。

4 結論

1) 建立的超螺旋滑模自抗擾控制器相對于非線性自抗擾控制減少了可調參數，降低了控制器調整難度。

2) 提高了永磁同步電機調速控制系統的魯棒性，加快了調速系統的響應速度，簡化了非線性自抗擾控制器的結構。