帶有薛定諤項的分數階基爾霍夫方程解的存在性研究
韓志玲,桑彥彬,于 雪
(中北大學 數學學院, 太原 030051)
0 引言
考慮如下分數階基爾霍夫型問題:
(1)
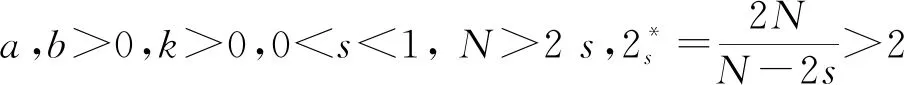
(2)

通過使用變分方法,得到解的存在性和多重性。2021年,文獻[2]利用不同的方法研究了基爾霍夫問題:
通過將其轉化為一個關于(u,λ)的等價方程組來得到原方程解的存在性。
另一方面,關于帶有臨界指數的分數階基爾霍夫問題,已有大量結論。文獻[3]通過Nehari流形和纖維映射研究了下列方程,得到了該問題非平凡解的存在性和不存在性:
文獻[4]證明了由非局部積分微分算子誘導的基爾霍夫問題非負解的存在性。文獻[5]研究了具有臨界指數的分數階基爾霍夫方程,利用變分方法得到了正基態解的存在性。更多關于帶有臨界指數的分數階薛定諤型問題的結果,可參見文獻[6-10]。
受上述文獻的啟發,把文獻[2]的整數階基爾霍夫問題推廣到帶有薛定諤項的分數階基爾霍夫問題中。目的是將基爾霍夫的非局部項和帶u的薛定諤項分離,從而轉化為等價的方程組,其中非線性項滿足次臨界增長、超線性條件,同時通過下控制函數的次數q的分類,最終建立方程(1)具有一個和2個非平凡解的存在性和不存在性。
證明方程(1)和方程組(2)等價性的方法與文獻[11]類似,通過3步獲得方程組(2)解的存在性。
首先,根據山路引理求解下列方程:
(3)
然后,當確定了u,立即可解出:
(4)
最后,借助于等價結果得出方程(1)解的存在性。
1 主要命題及定理
命題1方程(1)至少有一個非平凡解v∈Hs(RN)當且僅當方程組(2)至少有一個非平凡解(u,λ)∈Hs(RN)×R+。
假設f滿足如下條件:

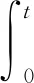
(H3) 當t→0時,f(t)=ο(t)。
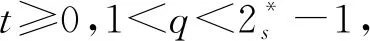
應用命題1,可以證明下面的定理。
定理1若f滿足條件(H1)—(H4),則下面結論成立:
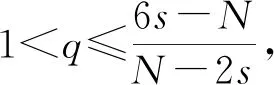
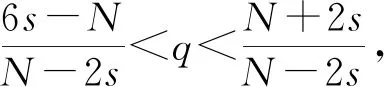
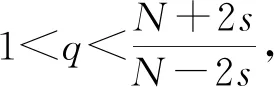
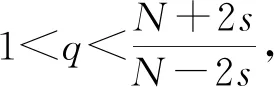
2 預備知識
在證明主要結果之前,給出一些有用的定義。分數階Sobolev空間Ds,2(RN)定義如下:
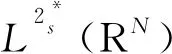
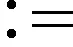
定義范數:
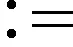

引理1存在正常數α>0,ρ>0,對任意的u∈?Bρ(0),有I(u)≥α。
證明對任意的C∈R,利用H?lder不等式,有:
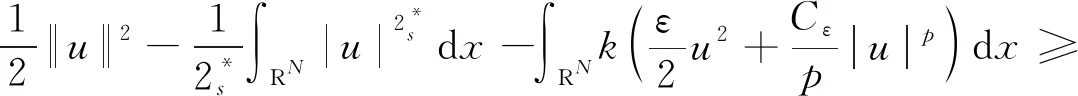
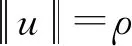
引理2存在e∈E,有I(e)<0。
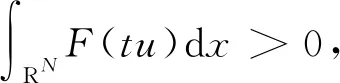
φ′(t)=-qt-q-1F(tu)+t-quf(tu)=t-q-1(-qF(tu)+tuf(tu))≥0
因此,對任意的t≥1,有F(tu)≥tqF(u)。則:
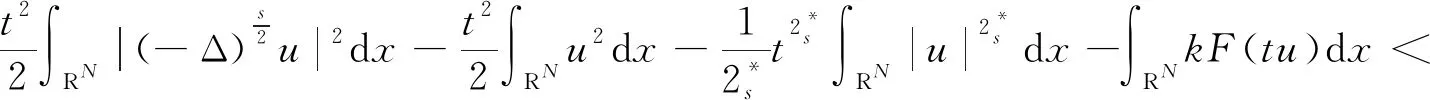
因為q>2,所以當t→∞時,I(tu)→-∞,取e=tu,得到結論,引理2成立。
通過引理1和2,知道I具有山路幾何結構,則定義I的山路水平集c為:
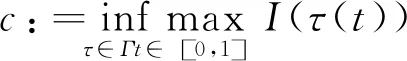
且Γ={τ∈C([0,1],E):τ(0)=0,I(τ(1))<0}。通過文獻[12]中的定理3知道,I有一個(C)c序列。
為了得到方程(3)的非平凡解,在這一部分估計山路水平集c。
從文獻[13]得到,在RN上,SN,s可由下列函數達到:
且
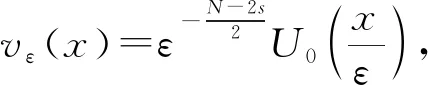
通過文獻[14]中命題21和22,可得到:
(5)
(6)
(7)
(8)
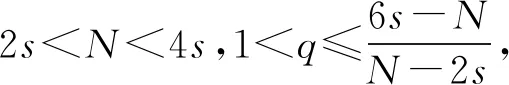
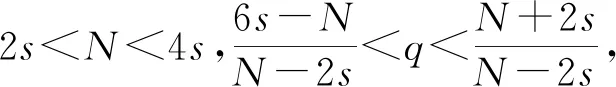
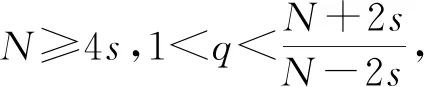
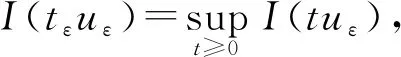
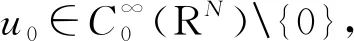
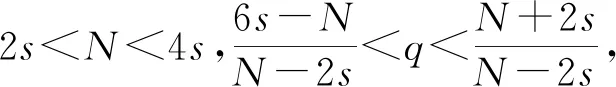
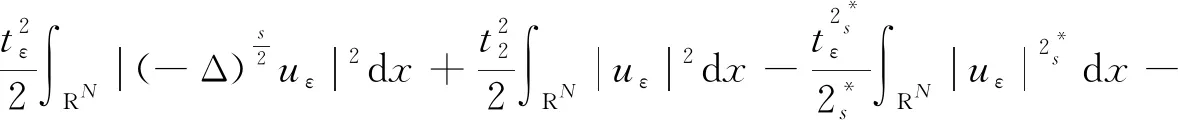
上式表明2)成立。
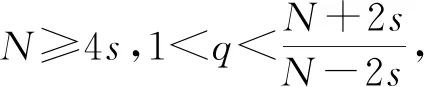
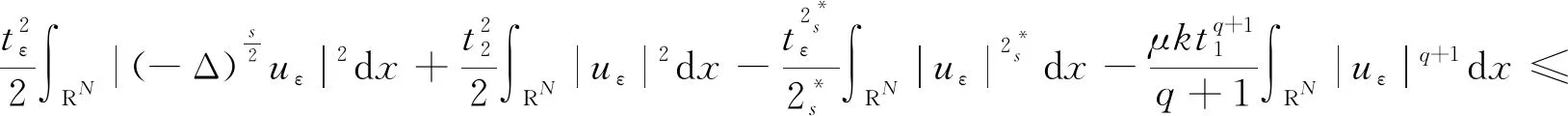
因此完成證明。
3 (C)c序列
引理4令c∈R,{un}是I的(C)c序列,則{un}是有界的。
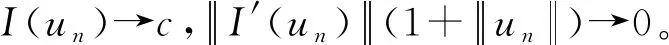
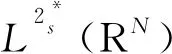
這表明在Hs(RN)中,{un}是有界的。
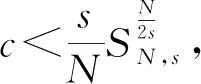
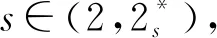
通過條件(H2),有:
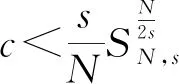
4 主要結果的證明
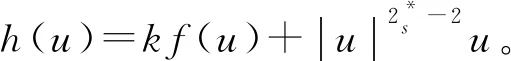
一方面,若方程(1)有解v∈Hs(RN),則:
令
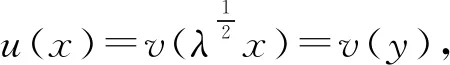
則:
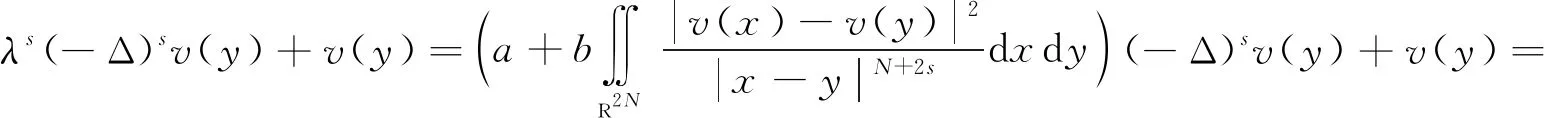
h(v(y))=h(u(x))
因此,(u,λ)∈Hs(RN)×R+是方程組(2)的解。
另一方面,若方程組(2)有解(u,λ)∈Hs(RN)×R+,有:
(-Δ)su+u=h(u),x∈RN
和
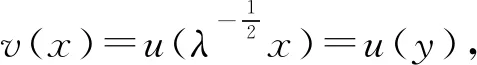
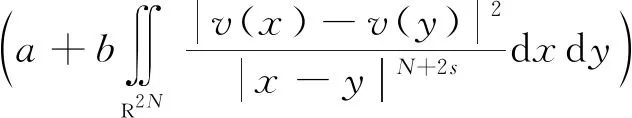
(-Δ)su(y)+u(y)=h(u(y))=h(v(x))
因此,v∈Hs(RN)是方程(1)的解,證畢。
定理1的證明由命題1和文獻[13]中的定理2.1和2.5,得到結論,證畢。
5 結論
對于帶有薛定諤項的分數階基爾霍夫型問題,即方程(1),通過對N、q、a和b進行不同的限制,并使用山路引理,最終分別得到原方程有一個非平凡解、兩個非平凡解和無解。

