柔性低頻輸電高頻諧振風險評估及抑制方法研究

華 文，林進鈿，裘 鵬，陸 翌，潘武略，張 靜，林藝哲

（1.國網浙江省電力有限公司電力科學研究院，杭州 310014；2.國網浙江省電力有限公司，杭州 310007；3.南京南瑞繼保工程技術有限公司，南京 211102）

0 引言

柔性低頻交流輸電技術在城市供區互聯及海上風電送出等場合具備一定的應用潛力，其核心設備為M3C（模塊化多電平矩陣變換器）。M3C采用全橋子模塊替代傳統矩陣式交-交變頻器的開關器件，具有模塊化、易于擴展、低諧波注入和功率因數可控等優點［1-3］。M3C的控制系統采用已經廣泛應用在電壓源型換流器中的雙環控制［4-5］，外環為功率控制器，內環為電流矢量控制器。然而，電壓源型換流器在具有快速動態過程的電流矢量控制下，易在高頻段呈現出負阻尼效應，如果與所接入系統阻抗匹配不當，會使系統產生高頻諧振［6-7］。在實際工程中已經多次出現此類事故：2013年，德國Borwin1海上風電經柔性直流（以下簡稱“柔直”）送出工程出現250～350 Hz 的高頻諧振，產生的諧波損毀了濾波器并導致工程長期停運［8］；2017 年，魯西背靠背柔直單元與受端交流系統發生1 270 Hz 高頻諧振，致使系統停運［9-11］；2018 年，在渝鄂柔直工程調試期間，系統中出現了1 810 Hz左右的高頻振蕩［12-13］。因此，急需對柔性低頻交流輸電工程的高頻諧振穩定性進行評估，并針對性地提出高頻諧振抑制策略。

目前，分析電力電子裝置并網穩定性的方法主要包括特征值分析法［14-15］和阻抗分析法［16-20］。特征值分析法是基于系統的狀態空間模型，通過求解特征值獲取系統的諧振模式并判斷其穩定性。但是，特征值分析法中狀態空間模型的階數通常較高，而且當系統運行方式改變時，需要重新建立模型，限制了特征值分析法的使用。阻抗分析法則是根據電力電子裝置等效阻抗和交流電網等效阻抗之間的匹配情況判斷整個系統的穩定性，近年來該方法取得了廣泛的應用。文獻［11-12］利用阻抗分析法研究了柔直換流器與交流電網產生高頻諧振的機理，分析表明電壓前饋中的延時環節是引發柔直系統高頻諧振的主要原因；文獻［21］提出在電壓前饋環節中附加帶阻濾波器，通過改善柔直換流器高頻段的阻抗特性，進而抑制柔直系統的高頻諧振；文獻［22］采用附加無源濾波裝置的思路，通過阻抗分析法分析了對于濾波裝置外特性的需求，并設計了二階RLC 高通濾波器實現高頻諧振的抑制。以上研究均針對柔直工程展開，而基于M3C的柔性低頻交流輸電系統的高頻諧振分析與抑制尚未見報道。

為了彌補現有M3C 高頻諧振問題研究的不足，降低實際工程運行中的高頻諧振風險，本文以規劃建設中的杭州工程為例，建立了M3C的高頻阻抗模型，在多種運行方式下評估了M3C與交流系統的高頻諧振風險，并分析了高頻諧振的產生機理。在此基礎上，提出了在M3C電壓前饋環節附加低通濾波器的高頻諧振抑制策略。最后，在PSCAD/EMTDC 中進行了電磁暫態仿真，驗證了分析結果的準確性和所提高頻諧振抑制策略的有效性。

1 M3C高頻阻抗模型

三相M3C 的主回路結構如圖1 所示，定義工頻側為輸入側，其電氣量下標用大寫字母（A、B、C）和字母i表示，低頻側為輸出側，其電氣量用小寫字母（a、b、c）和字母o 表示。M3C 由3 個子換流器和9個橋臂組成，每個橋臂包含N個級聯子模塊、橋臂電感L0和橋臂電阻R0。正常運行時，M3C 的輸入側和輸出側分別在輸入、輸出頻率下進行dq坐標變換，并通過各自的外環功率控制器和內環電流控制器實現解耦控制。

圖1 M3C基本拓撲結構

杭州柔性低頻交流輸電工程分別在中埠站和亭山站建設M3C換頻站，實現杭州富陽供區和昇光供區之間的柔性互聯，換頻站的主要參數如表1所示。通常，電力電子換流器受dq控制不對稱的影響存在頻率耦合效應，在阻抗特性方面，表現為正負序阻抗間的耦合。但是，已有的很多研究表明，頻率耦合效應僅在中低頻段有較大影響，在高頻段影響較小，高頻段換流器的正負序阻抗可以近似解耦且趨于一致，因此忽略耦合項后的一維阻抗對于分析高頻振蕩問題已經足夠準確［23-24］。考慮M3C 控制系統延時分別為300 μs、400 μs、500 μs 和600 μs 的情況，在PSCAD/EMTDC 中對杭州工程的電磁暫態仿真模型進行阻抗掃描，可以得到兩個M3C工頻側和低頻側的阻抗特性，如圖2—圖5中的各條虛線所示。阻抗掃描的具體方法為：針對某一頻率，在M3C一側施加該頻率下的小信號諧波電壓，提取對應的諧波電流，諧波電壓與諧波電流的比值即為該頻率下的等效諧波阻抗［25-27］。

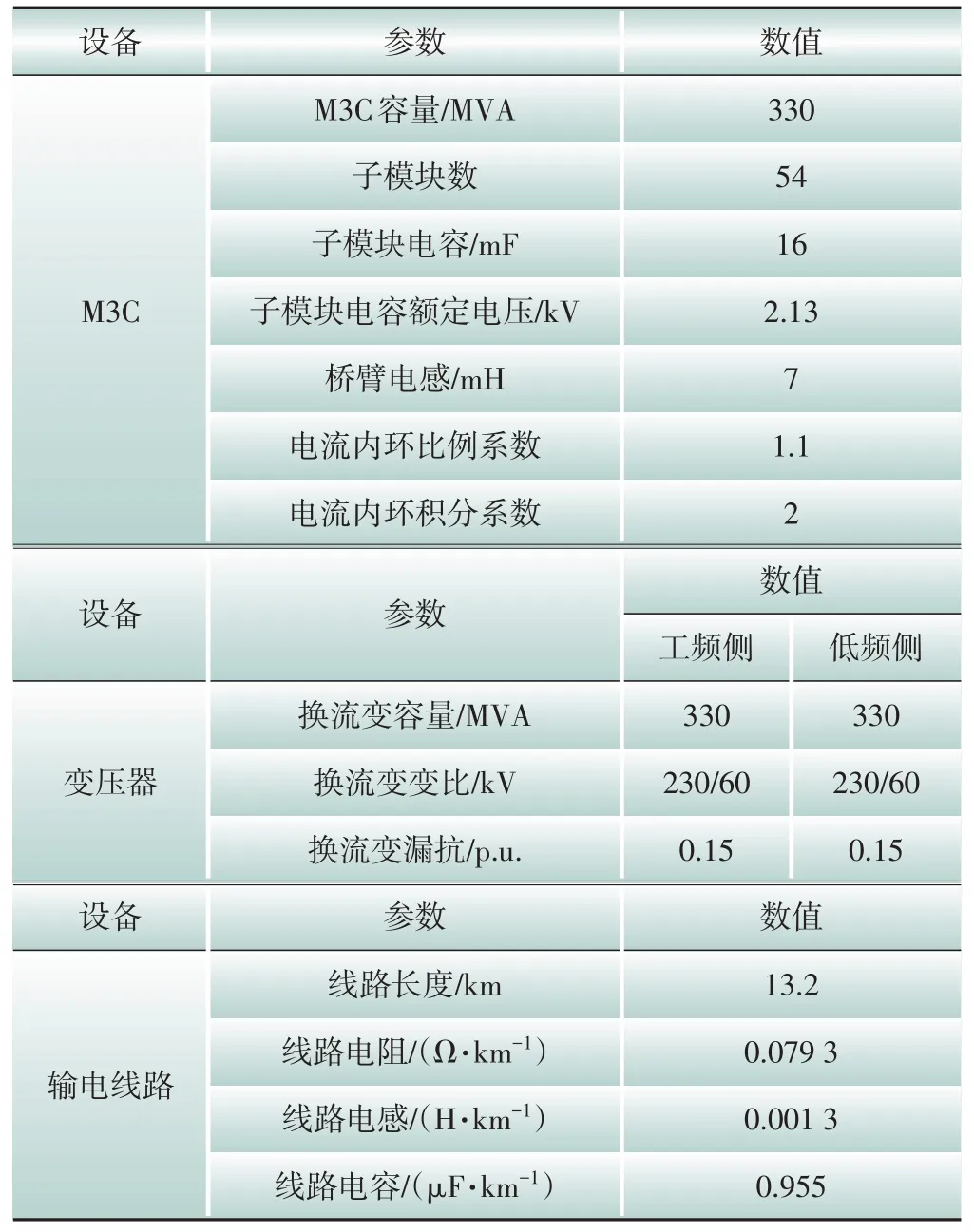
表1 杭州工程主要參數

2 柔性低頻輸電系統高頻諧振評估

本文以杭州工程為例，在多種運行方式下分析了系統的高頻諧振風險。對于M3C，分別考慮其控制系統延時為300 μs、400 μs、500 μs 和600 μs 的情況。對于工頻側交流系統，考慮以下兩類拓撲結構：

1）交流系統完整運行。

2）連接換頻站和與換頻站直接相連節點的輸電線路中，一條輸電線路發生N-1斷線。對于低頻側交流系統，其拓撲結構簡單，僅包含一條輸電線路，因此僅考慮一種拓撲結構。

2.1 工頻側系統高頻諧振評估結果

根據阻抗分析法［16］，工頻側系統的高頻諧振穩定性可由交流系統與M3C阻抗幅值相交時的相角差判斷。若交流系統與M3C阻抗之間的相角差超過180°，則系統中會發生不穩定高頻諧振。

M3C 延時分別為300 μs、400 μs、500 μs 和600 μs 時，亭山站M3C 工頻側阻抗如圖2 中各條虛線所示。在工頻側，與亭山站直接相連的節點有荷花站和昇光站，當交流系統正常運行以及連接亭山站、荷花站和昇光站的其中一條輸電線路發生N-1 斷線時，亭山站工頻側交流系統阻抗掃描結果如圖2中的各條實線所示。

根據圖2可知，在上述各種運行方式下，交流系統阻抗幅值與亭山站M3C工頻側阻抗幅值均不存在交點。因此在所考慮的運行方式范圍內，亭山站M3C 不會與其工頻側交流系統產生高頻諧振。

圖2 亭山站工頻側系統阻抗分析

M3C 延時分別為300 μs、400 μs、500 μs 和600 μs 時，中埠站M3C 工頻側阻抗如圖3 中各條虛線所示。在工頻側，與中埠站直接相連的節點有富陽站和龍隱站，當交流系統正常運行以及連接中埠站、富陽站和龍隱站的其中一條輸電線路發生N-1 斷線時，中埠站工頻側交流系統阻抗掃描結果如圖3中的各條實線所示。

圖3 中埠站工頻側系統阻抗分析

當延時為300 μs 時，一種N-1 斷線工況下的交流系統阻抗幅值與M3C 阻抗幅值在1 880 Hz 處存在交點，二者相角差為159°，因此不會導致系統出現不穩定高頻諧振；當延時為400 μs 時，一種N-1斷線工況下的交流系統阻抗幅值與M3C阻抗幅值存在2個交點，最大相角差出現在1 860 Hz處，達到178°，在這種工況下，系統相角裕量不為負但裕度不足，對系統運行不利；當延時為500 μs 和600 μs 時，交流系統阻抗幅值與M3C 阻抗幅值不存在交點，此時系統不會產生高頻諧振。

2.2 低頻側系統高頻諧振評估結果

低頻側系統結構如圖4（a）所示。低頻系統電壓由中埠站控制，中埠站低頻側等效電路如圖4（b）所示，根據阻抗分析法［16］，其高頻諧振穩定性由ZM3C1與Zeq1幅值相交時的相角差判斷；亭山站低頻側等效電路如圖4（c）所示，其高頻諧振穩定性由Zeq2與ZM3C2幅值相交時的相角差判斷。Zeq1和Zeq2分別為：

圖4 杭州工程低頻系統結構

當M3C延時分別為300 μs、400 μs、500 μs和600 μs 時，中埠站M3C 低頻側阻抗ZM3C1如圖5 中各虛線所示，Zeq1如圖5 中各實線所示。當延時為300 μs 和400 μs 時，ZM3C1與Zeq1阻抗幅值無交點；當延時為500 μs時，ZM3C1與Zeq1阻抗幅值在720 Hz頻率處相交，相角差為134°；當延時為600 μs時，ZM3C1與Zeq1阻抗幅值在780 Hz 頻率處相交，相角差為171°。因此中埠站M3C 低頻側不存在高頻諧振風險。

圖5 中埠站低頻側系統阻抗分析

M3C 延時分別為300 μs、400 μs、500 μs 和600 μs 時，亭山站M3C 低頻側阻抗ZM3C2如圖6 中各虛線所示，Zeq2如圖6 中各實線所示。當延時為300 μs時，ZM3C2與Zeq2阻抗幅值在580 Hz頻率處相交，相角差為158°；當延時為400 μs 時，ZM3C2與Zeq2阻抗幅值在540 Hz 頻率處相交，相角差為150°；當延時為500 μs時，ZM3C2與Zeq2阻抗幅值在720 Hz 頻率處相交，相角差為152°；當延時為600 μs時，ZM3C2與Zeq2阻抗幅值在730 Hz頻率處相交，相角差為168°。因此中埠站M3C 低頻側不存在高頻諧振風險。

圖6 亭山站低頻側系統阻抗分析

綜上所述，在所考慮的運行方式下，亭山站工、低頻系統和中埠站低頻系統不存在高頻諧振風險，中埠站工頻系統可能出現交流系統阻抗與M3C 阻抗相角差接近180°的情況，若考慮到運行時運行條件的變化使相角差進一步增大，則會導致系統失穩，因此中埠站工頻系統存在一定的高頻諧振風險。

3 高頻諧振抑制策略

3.1 高頻諧振機理分析

根據第2章的分析，在柔性低頻交流輸電系統的工頻側存在相角裕度不足的工況，表現出了一定的高頻諧振風險，其根本原因在于部分頻段內M3C 的相角過大，呈現負電阻電感特性，與呈現容性特征的交流系統發生諧振。

M3C 運行時，工頻側和低頻側分別在各自頻率下進行dq坐標變換，并實現解耦控制，即其中任意一側的交流側輸出電流并不受另一側控制器的影響。且已有研究表明，子模塊電容動態以及帶寬較低的外環控制與鎖相環對換流器高頻段的影響很小，內環控制、電壓前饋和延時因素對換流器高頻段影響較大［7，20］。鑒于此，可以得到考慮內環控制、電壓前饋和延時因素影響的M3C工頻側簡化控制框圖，如圖7所示。

圖7 中：Iref為輸入側或輸出側的電流指令值；Iout為該側的輸出電流；Ugird為該側電網電壓；Km為調制環節系數；R為等值電阻，R=R0/3；L為等值電感，L=Ls+L0/3，其中Ls為該側變壓器漏電感；Gpi為內環pi 控制器的傳遞函數；GT1和GT2分別為電流、電壓測量的延時環節，如式（3）所示。

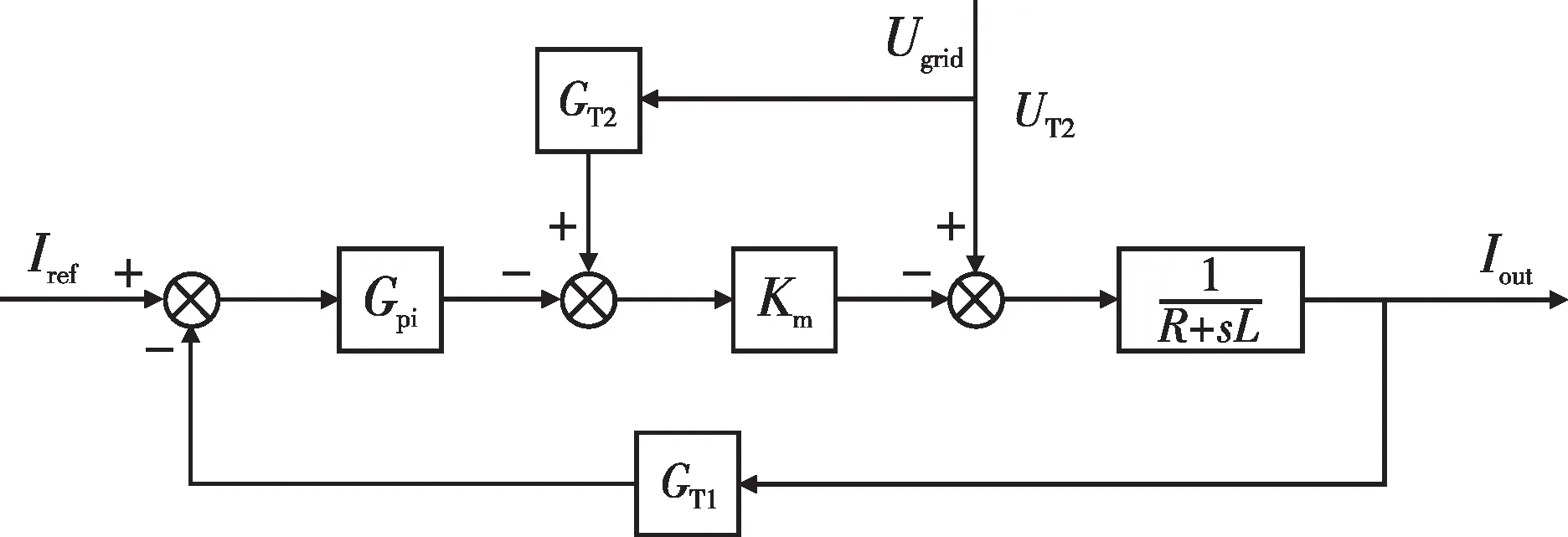
圖7 M3C簡化控制框圖

根據圖7得到的輸出電流的表達式為：

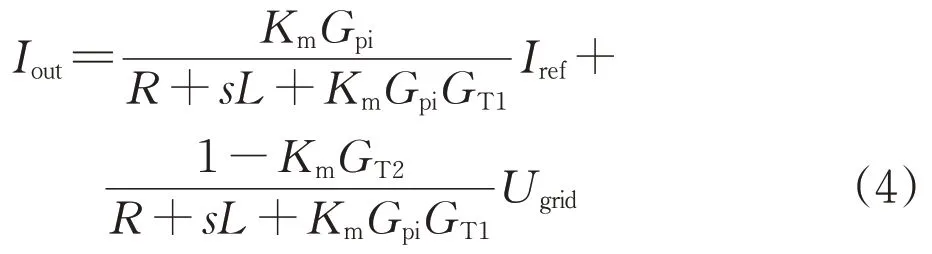
因此M3C工頻側高頻阻抗表達式為：

當延時為400 μs 時，中埠站工頻側高頻阻抗的理論計算結果和PSCAD 掃頻結果對比，如圖8所示。可以看出，根據式（5）得到的理論計算結果與掃頻結果基本一致。

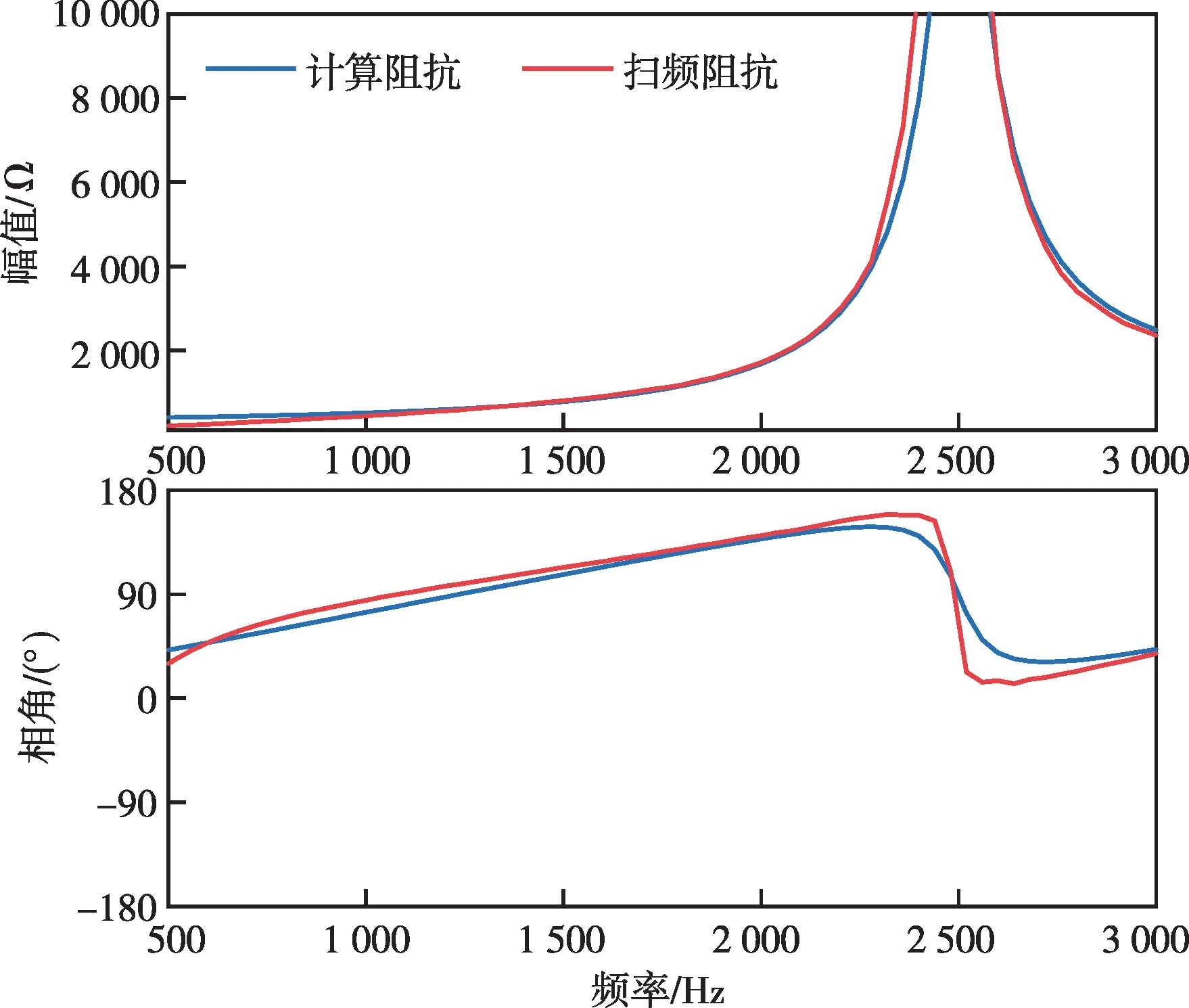
圖8 計算阻抗與仿真掃頻阻抗對比

根據式（5），M3C 的高頻阻抗為ZM3C=Z1Z2，其中Z1和Z2可分別表示為：

以電壓、電流測量環節延時400 μs為例，圖9給出了ZM3C、Z1和Z2的相頻曲線。根據圖9 可知，Z1在高頻段相角近似為90°，表現為電感特性，當Z2相角為正時，由于∠ZM3C=∠Z1+∠Z2，ZM3C相角將大于90°，此時M3C阻抗與交流系統阻抗間的相角差可能會接近或超過180°。若通過阻抗重塑策略將M3C阻抗相角限制在90°以下，由于交流系統阻抗相角在±90°之間，則交流系統阻抗與M3C阻抗間的相角差不會超過180°，系統不會產生不穩定高頻諧振。具體地，Z1在高頻段表現為電感特性，結合式（6）可知，這是因為其相角特性主要由其表達式中的sL項決定，受控制系統影響較小，因此難以通過控制策略改變其相角特性；Z2僅受電壓前饋環節影響，因此通過重塑電壓前饋通道特性可以改變Z2的相頻特性，進而實現對ZM3C的阻抗重塑。

圖9 ZM3C、Z1和Z2的相頻曲線

3.2 高頻諧振抑制策略

本文選擇在電壓前饋環節中附加二階低通濾波器的M3C阻抗重塑策略，如圖10所示。濾波器表達式見式（7），其中f0為低通濾波器截止頻率，ζ為阻尼比。附加低通濾波器后，Z2=1/（1-KmGfilterGT2），在高頻段由于濾波器的低通特性，Gfilter≈0，Z2≈1，因此∠Z2≈0°。

圖10 附加低通濾波器后M3C簡化控制框圖

以工頻側出現相角裕量不足的運行方式為例，選擇f0=500 Hz，ζ=0.707。附加低通濾波器后，M3C和交流系統阻抗對比如圖11所示。根據圖11可知，附加低通濾波器后M3C阻抗相角減小到90°附近，M3C 阻抗幅值與交流系統阻抗幅值存在兩個交點，最大相角差出現在1 835 Hz 處，相角差為104°，原先相角裕量不足的情況得以改善。

圖11 附加低通濾波器后M3C阻抗與交流系統阻抗對比

4 高頻諧振抑制策略驗證

根據第2章的分析可知，柔性低頻交流輸電系統的高頻諧振風險來自于呈負電阻電感特性的M3C與呈容性的交流系統間的諧振。在PSCAD/EMTDC 中搭建圖12 所示的仿真系統，M3C 的主要參數與表1中一致，延時為400 μs，低頻側接入理想電源，工頻側經過并聯支路后接入電源，參數如表2所示，可以模擬呈現容性特征的交流系統。

圖12 仿真系統示意圖

表2 工頻側交流系統參數

圖13給出了M3C工頻側阻抗與工頻側交流系統阻抗對比結果。在M3C 工頻側接入系統1 時，系統諧振頻率為1 540 Hz，諧振點處阻抗相角差為178°，裕度不足；在M3C工頻側接入系統2時，諧振頻率為1 590 Hz，諧振點處阻抗相角差為183°，系統會出現高頻諧振失穩。電壓前饋環節附加f0=500 Hz、ζ=0.707 的二階低通濾波器后，M3C 工頻側阻抗與工頻側系統阻抗的對比結果如圖14 所示。在圖14 中，當接入系統1 時，諧振點處阻抗相角差變為146°，當接入系統2時，諧振點處阻抗相角差變為146°。

圖13 M3C無附加低通濾波器時仿真系統的阻抗分析

圖14 M3C附加低通濾波器時仿真系統的阻抗分析

在PSCAD/EMTDC 仿真模型中，使系統運行進入穩態，0.5 s 時工頻側交流系統切換至系統1，0.6 s 時投入低通濾波器。圖15（a）給出了交流系統A 相電壓仿真波形，0.5 s 時A 相電壓出現高頻諧波，由圖15（b）的諧波分析結果可知，諧波分量主要為30 次諧波，投入低通濾波器后該諧波分量消失。

圖15 M3C接入系統1時仿真波形和諧波分析

在PSCAD/EMTDC 仿真模型中，使系統運行進入穩態，0.5 s 時工頻側交流系統切換至系統2，0.6 s 時投入低通濾波器。圖16（a）給出了交流系統A 相電壓仿真波形，0.5 s 時A 相電壓發生不穩定高頻諧振，由圖16（b）的諧波分析結果可知，其諧波分量主要為31次和33次諧波，投入低通濾波器后高頻諧振得以抑制。

圖16 M3C接入系統2時仿真波形和諧波分析

綜上所述，對于諧振點處阻抗相角差接近180°的系統相角裕量不足的情況和相角差超過180°的系統失穩的情況，均可以通過在電壓前饋環節中附加低通濾波器得到改善。仿真結果與理論分析基本一致，驗證了理論分析的準確性和所提高頻諧振抑制策略的有效性。

5 結論

本文對柔性低頻交流輸電系統的高頻諧振風險進行了評估，分析了系統產生高頻諧振的機理，提出了在電壓前饋環節中附加低通濾波器的高頻諧振抑制策略，并在PSCAD/EMTDC 中進行仿真，驗證了所提策略的有效性，具體得到以下結論［28-31］：

1）針對杭州工程，在所考慮的工況范圍內，亭山站工、低頻系統和中埠站低頻系統不存在高頻諧振風險，中埠站工頻系統存在一定的諧振風險，諧振風險大小與M3C電壓前饋環節延時和交流系統運行方式有關。

2）在高頻段的部分頻段內，電壓前饋環節延時在原先90°附近的M3C相角上又疊加了一個正角度，使M3C整體阻抗相角超過90°，從而導致某些諧振頻率點上交流系統與M3C 阻抗相角差過大，給系統引入了高頻諧振風險。通過在電壓前饋環節中附加低通濾波器，可以將M3C阻抗相角限制在90°附近，避免出現交流系統與M3C阻抗相角差過大的情況，有效地降低了系統發生高頻諧振的風險。