考慮風光互補特征的多微網系統自治經濟調度模型

吉 祥，謝 敏，曾 東，張 昕，吳 偉，尹 起，付世杰，吳子杰

（1.國網浙江省電力有限公司嘉興供電公司，浙江 嘉興 314000；2.華南理工大學 電力學院，廣州 510640）

0 引言

隨著環境污染、氣候變化等問題凸顯，世界各國逐步開始向能源低碳化、可持續發展轉型。中國正積極推動能源電力系統根本性變革，構建綠色低碳可持續發展的現代能源體系，提出“雙碳”目標。2030年風電太陽能發電裝機容量將超過12億kW，非化石能源占一次能源消費比重將提升至25%。風電和光伏等可再生能源的零碳排放和清潔型特征，對于促進能源結構轉型、構建新型電力系統具有重要意義。隨著可再生能源滲透率持續提高，風電、光伏固有的隨機性及波動性對高比例可再生能源電力系統穩定機理、調度運行和規劃發展方面產生深刻影響。

多微網系統是微網系統的延伸和深化，能夠有效應對隨機波動性對配電網的沖擊，促進提升可再生能源消納水平。電力市場中，不同微網隸屬于不同的利益主體，具有隱私性特征，傳統的電力調度方式無法準確反映不同微網主體的利益訴求；同時，同區域的風光出力呈現天然互補性［1］，高比例可再生能源接入時考慮協同作用和互補效益能提高能源利用率。因此，研究考慮風光互補特征的多微網自治經濟調度具有十分重要的意義。

從已有的研究來看，多微網能量管理從調度角度分為集中式控制、分布式控制兩種模式［2］，集中式分層控制將微網、配電網作為整體進行優化調度，分布式控制將微網、配電網作為獨立的個體分別建模。文獻［3］建立多微網互聯系統的協調調度模型，應用粒子群優化算法求解。文獻［4］基于儲能電站服務，構建冷熱電多微網運轉模式，并構建混合整數線性規劃模型。文獻［5］對一致性算法、交替方向乘子法、分布式梯度下降算法等分布式協同控制算法進行歸納分析。文獻［6］考慮負荷的綜合需求響應模型，建立主從博弈的多微網綜合能源系統優化調度策略。文獻［7］提出一種面向多微網能源協調交易的共治決策方法，采用層次分析法實現多微網系統分散式決策和分布式能量管理。文獻［8-9］利用ATC（目標級聯分析法）提出分布式優化調度方法。以上研究實現了多微網系統能量優化管理，但并未充分考慮同區域風光互補特征對多微網經濟調度的影響。

基于以上研究，本文充分考慮多微網分散自治特點以及風電、光伏等新能源的隨機性和相關性，構建考慮風光互補特征的多微網自治經濟調度模型。首先基于核密度估計和Copula 理論，結合拉丁超立方抽樣及場景縮減形成典型場景生成方法；其次以多場景下多微網系統經濟運行成本、場景轉移費用最優為目標，建立考慮風光相關性的多微網雙層優化調度模型；應用ATC，構建兼顧配電網與各微網系統利益的并行求解方法；最后以IEEE 33 節點系統為例，通過比較考慮風光相關性與僅考慮隨機性情景的綜合費用，分析風光互補特征對系統經濟性及安全性的影響，為安全經濟調度提供輔助決策。

1 多微網系統結構

區域多微網系統中，各微網在局部區域內將分布式能源和用戶整合在一起，當各微網產能過剩或者不足時，微網中央控制器通過聯絡線與配電網進行能量交互。多微網系統在配電網故障時提供電力支撐，保障非故障區域可靠供電；同時，也可作為可調節負荷實現削峰填谷的功能［10］。

在電力市場環境下，多微網系統優化運行控制策略如圖1所示。各微網與配電網分屬于不同的利益主體，配電網及各微網控制模塊分別統籌區域內發電機及負荷以實現效益最優，監測各類設備運行工況，并實時將電氣參數等運行數據傳遞至多微網系統能量管理系統。能量管理系統作為多微網系統運行控制的核心，通過功率控制、負荷管理及潮流管控等功能維持電壓、頻率穩定，實現系統運行安全；長期運行管理模式下，綜合考慮系統運行目標、機組出力、負荷用電等需求制訂合理調度策略，建立優化調度模型，選取合適的算法實現多微網系統綜合成本最小、促進新能源消納等優化目標。配電網及各微網控制模塊收到能量管理系統的優化策略后快速予以響應。

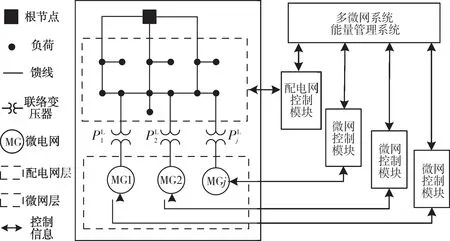
圖1 多微網系統運行控制策略

2 考慮風光相關性的場景生成方法

同時建有風電、光伏機組的微網，風電場和光伏電站地理位置臨近，有功出力呈現相關性和互補性特征［11］。隨著新能源滲透率持續提高，分析風光互補特征對多微網系統經濟調度的影響具有重大實際價值。Copula 理論是描述多維隨機變量相互關系的重要工具，Sklar 定理論證了Copula函數將聯合分布與邊緣分布函數聯接的可行性與唯一性［12］。基于Copula 理論，風光出力聯合分布函數可由風電、光伏邊緣分布與Copula 函數連接生成。本文基于Copula 理論及拉丁超立方抽樣，提出風電、光伏典型場景生成方法，流程如下：

1）基于風電、光伏歷史出力樣本，運用核密度估計法計算風電場出力x、光伏出力y的概率密度函數（累積分布函數及密度函數）。

2）基于Copula理論，運用極大似然函數法對5類常用Copula 函數（Gaussian 函數、t 函數、Gumbel 函數、Clayton 函數、Frank函數）的未知參數α進行估計，建立Copula聯合分布函數。

3）綜合Spearman相關性系數、Kendall相關性系數、歐式距離、最大距離這4 類指標，對5 種Copula 函數的擬合優度進行評價。其中Spearman相關性系數、Kendall 相關性系數表征隨機變量間的相關性程度；歐式距離、最大距離檢驗函數分布與樣本的擬合程度，其值越小表明擬合程度越好。與樣本相關性系數接近、擬合指標值最小者作為最優Copula函數。

4）根據Copula理論，風光聯合密度函數h（x，y）為風光出力邊緣密度函數與Copula 函數的乘積，即h（x，y）=c（F（x），F（y）；α）·f（x）·f（y），其中，F（x）和f（x）分別為風電場出力x的邊緣分布函數和邊緣密度函數；F（y）和f（y）分別為光伏出力y的邊緣分布函數和邊緣密度函數；c（F（x），F（y）；α）為Copula密度函數。

5）選取最優Copula 函數構建風光聯合密度函數，根據該分布函數拉丁超立方抽樣最終生成N個具有風光相關性特征的出力場景。

抽樣生成的樣本數量龐大，導致計算量增加，因此本文基于概率距離的快速前代消除技術將相似度較高的場景進行削減，生成Ns個誤差場景并計算各場景對應的概率，使得削減生成的誤差場景盡可能地符合風光出力場景的隨機互補特征。

3 多微網系統經濟調度模型

根據區域多微網系統結構和運營策略，配電網與微網分屬于不同運營商。各運營商通過部分信息交互追求各自效益最優。多微網系統以滿足安全運行為前提，最大程度滿足風光清潔能源消納，各運營商優化時通過聯絡線交互功率相互影響、彼此關聯，其經濟調度具有雙層優化問題的特征。

3.1 上層配電網經濟調度模型

3.1.1 上層配電網目標函數

配電網層運行目標為機組運行成本與各微網功率購售收益之和最優，其目標函數表述為：

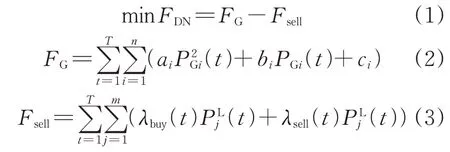
式中：FDN、FG、Fsell分別為配電網運行成本、配電網發電機運行成本、配電網與各微網功率交互成本；T為調度周期；n為配電網機組數量；PGi(t)為常規機組i在t時刻的出力，ai、bi、ci為機組i的發電成本系數；m為微網數量；為配電網在t時刻與微網j的傳輸功率，其值為負則表示配電網向微網購電；λbuy(t)和λsell(t)分別為t時刻對應的購電和售電價格。

3.1.2 上層配電網約束條件

配電網層運行時需滿足功率平衡約束，常規機組出力上下限、機組爬坡約束，聯絡線傳輸限額約束，同時留有旋轉備用容量確保安全運行，具體如下：

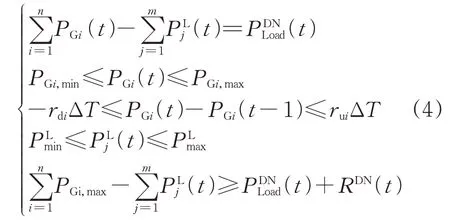
式中：ΔT為時間間隔；為配電網在t時刻的預測負荷；PGi，min和PGi，max分別為常規機組i的出力下限和上限；rdi和rui分別為機組i向下和向上爬坡速率；分別為聯絡線傳輸功率最低和最高限額；RDN(t)為配電網t時刻的備用容量。

3.2 下層微網經濟調度模型

風光功率預測是微網經濟調度的先決條件，以風光聯合密度函數為基礎，按照第2章場景生成方法生成考慮風光相關性的典型場景，應用場景法建立微網經濟調度模型，即微網在風電、光伏預測場景及典型場景（誤差場景）下制訂機組出力計劃。

3.2.1 下層各微網目標函數

3.2.2 下層各微網預測場景約束條件

在預測場景下，微網經濟調度需滿足以下約束條件。

1）功率平衡約束為：

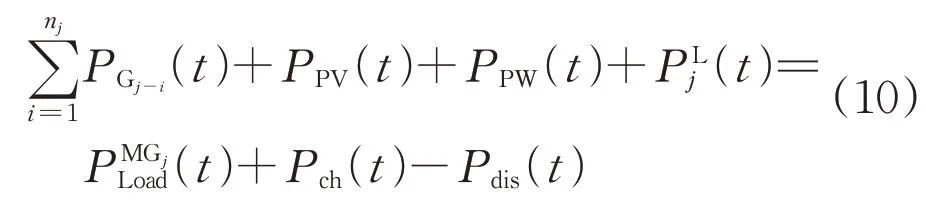
式中：PPV和PPW分別為光伏和風電發電功率；為微網j預測負荷。

2）各設備出力上下限及爬坡約束為：

目標管理是進行任何一項管理工作的基本方法和手段，成本控制也應遵循這一原則，即目標設定、分解、責任到位和成本執行結果、評價和目標修正，從而形成目標管理的計劃、實施、檢查、處理的循環.在實施目標管理過程中，目標的設定應切合實際，更落實到各部門、班組甚至個人；目標責任應全面，既有工作責任，更有成本責任[3].

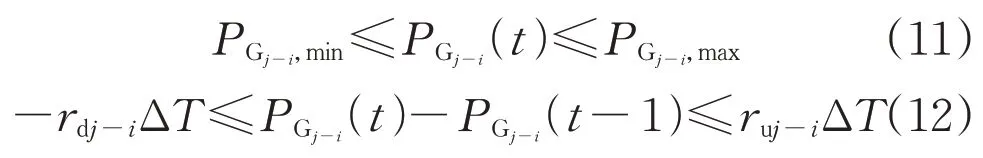
3）聯絡線功率交互約束為：

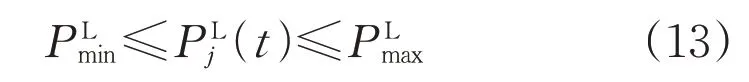
4）儲能裝置約束為：

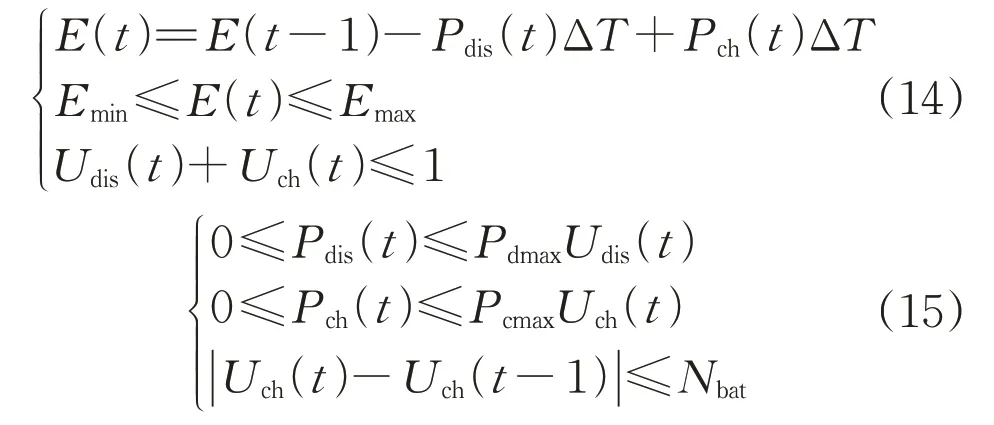
式中：E（t）為儲能裝置容量狀態；Emin和Emax為儲能裝置容量的下限和上限；Uch（t）和Udis（t）分別為儲能設備充電和放電0-1狀態變量；Pcmax和Pdmax分別為充電和放電功率限額；Nbat為充放電狀態轉換次數限制。

式（14）為儲能裝置運行約束條件，式（15）為儲能裝置充放電限值約束條件。

3.2.3 下層各微網誤差場景約束條件

微網在滿足預測場景運行約束的同時，需同時保證誤差場景s下穩定運行。參照預測場景約束條件，誤差場景s下的約束條件為：

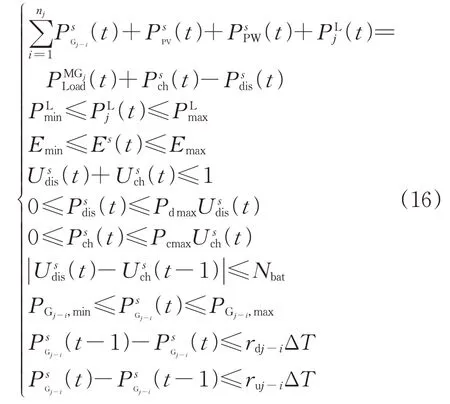
為確保風光出力由預測場景向誤差場景波動時，機組留有足夠的調節裕度保障區域微網運行穩定，微網需滿足場景轉移約束：

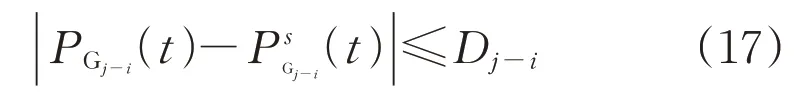
4 考慮風光相關性的多微網自治優化經濟調度模型

4.1 基于ATC的分層求解方法

按照第3 章模型，配電網與微網模型彼此關聯，聯絡線傳輸功率存在一致性約束。上、下層模型具有高度耦合性，無法獨立求解。ATC常用于解決復雜系統優化設計問題，在航天、汽車等結構設計領域已有成熟應用。其將復雜系統分解為子系統進行優化，各子系統將一致性約束以罰函數形式引入目標函數，實現并行獨立求解。計算中罰函數乘子不斷更新迭代直至共享變量（耦合變量）一致，達成系統最優目標。罰函數形式和乘子更新方式靈活，可采用二次函數、基于泰勒展開的對角線二次近似函數、拉格朗日函數等作為罰函數，其收斂性和最優性經過嚴格的理論證明［13］。ATC的分層優化思想與多微網自治優化經濟調度特征一致。

上層配電網優化經濟調度時，需要考慮微網與配電網間的功率交互。在配電網優化目標中，增加拉格朗日罰函數項表征配電網與微網的偏差，因此上層目標函數修正見式（18），約束由式（4）構成；同理下層各微網優化經濟調度時需考慮交互功率影響，各微網目標函數增加罰函數后修正見式（19），約束由預測場景約束（10）—（15）及誤差場景約束（16）、（17）構成。

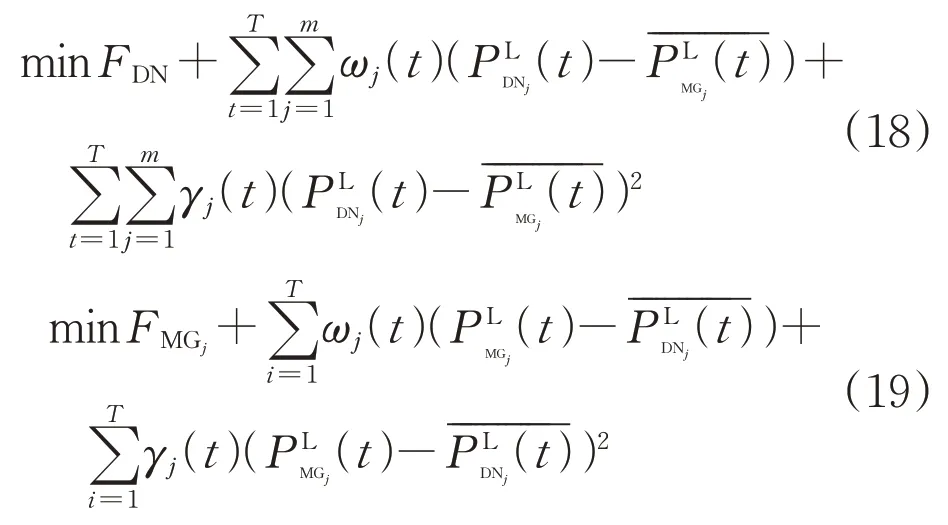
式中：ωj(t)和γj(t)為拉格朗日罰函數乘子；為多微網系統配電網與微網j的計劃交互功率；為微網j優化后向上層配電網傳遞的虛擬交互功率；為微網j的計劃交互功率；為配電網優化后向下層微網j傳遞的虛擬交互功率。

基于ATC實現上層配電網與下層各微網經濟調度問題的解耦，微網與各微網自主優化、交替迭代實現系統最優，其收斂滿足以下檢驗條件：

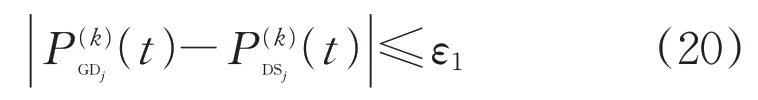
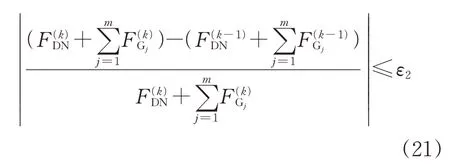
式中：上標（k）表示第k次迭代，下同；ε1和ε2為收斂精度。

式（20）為共享變量一致性檢驗條件，式（21）為總體效益最大化檢驗條件。

若迭代時不滿足收斂條件，則更新罰函數乘子，進入下一次迭代［14］：

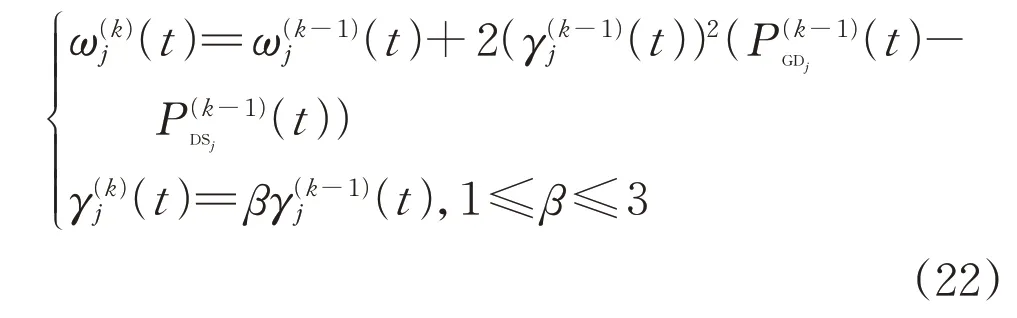
4.2 算法求解流程

考慮風光相關性的多微網自治優化經濟調度模型求解流程如圖2所示。

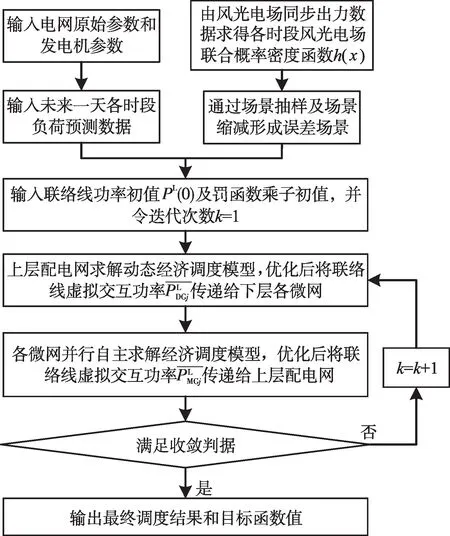
圖2 算法求解流程

5 算例分析

5.1 風光出力典型場景生成

選取湖北孝感某園區2014 年風電場及光伏電場歷史輸出功率為樣本，采樣周期為1 h。按照月份統計樣本日均出力情況，并分析風光出力相關系數，結果如圖3所示。

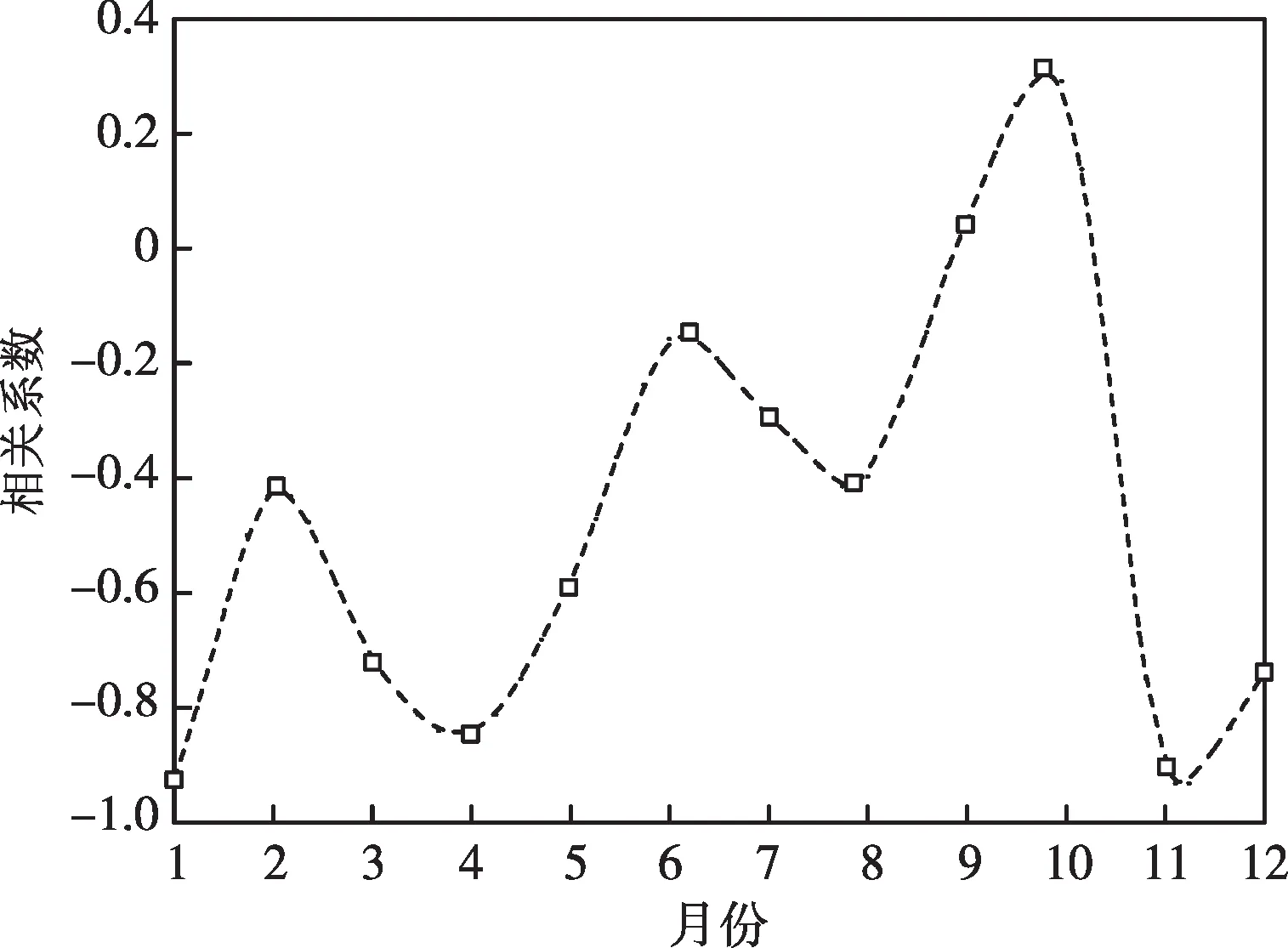
圖3 湖北某地區風光出力相關系數

從圖3 可以看出，風電場和光伏發電僅在9月、10 月呈現弱正相關性，其余月份相關系數均為負值，且1月、4月、11月呈現明顯的負相關特征。因此，有必要在多微網經濟調度問題中考慮風光互補特征的影響。

按照第2節方法開展核密度估計求出風光累計分布函數，采用極大似然函數法對5 類Copula 函數進行參數估計，評價指標值見表1。

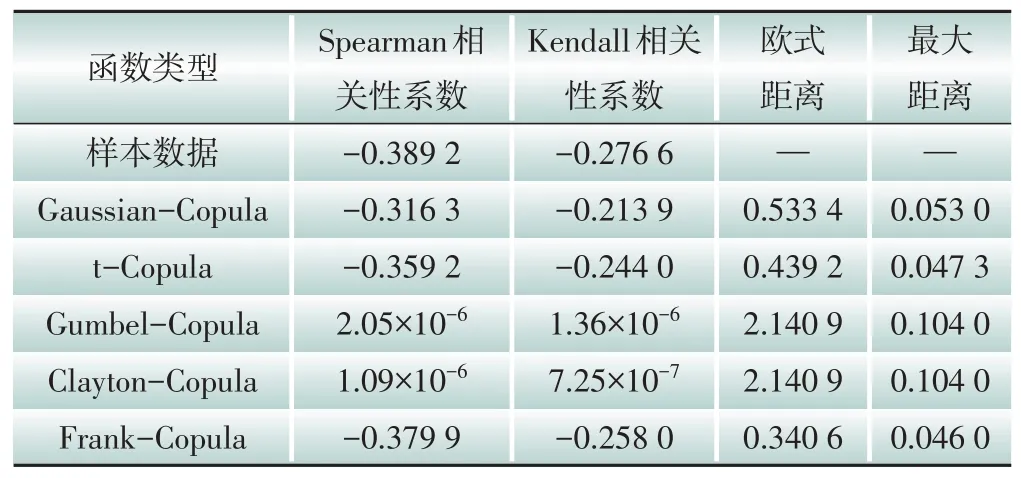
表1 各類Copula函數評價指標值

從表1 可以看出Gumbel-Copula、Clayton-Copula 兩類函數的相關性為正相關，與樣本的負相關性不符，且歐式距離及最大距離最大，擬合效果不佳。Gaussian-Copula、t-Copula、Frank-Copula 三類Copula 函數均能呈現樣本的負相關特征，且歐式距離及最大距離較小，適宜用于風光聯合建模。其中Frank-Copula 函數相關性與樣本最接近，且擬合性能最好，因此選取該函數作為最優Copula函數。

基于Copula函數抽樣生成1 000組數據，并經過場景削減形成5個典型風光出力場景。以風電出力為例對生成場景進行分析，5個誤差場景風電場統計如圖4所示，誤差場景出力覆蓋風電場預測出力及實際出力曲線，表明生成的場景能有效反映風電出力隨機特征。

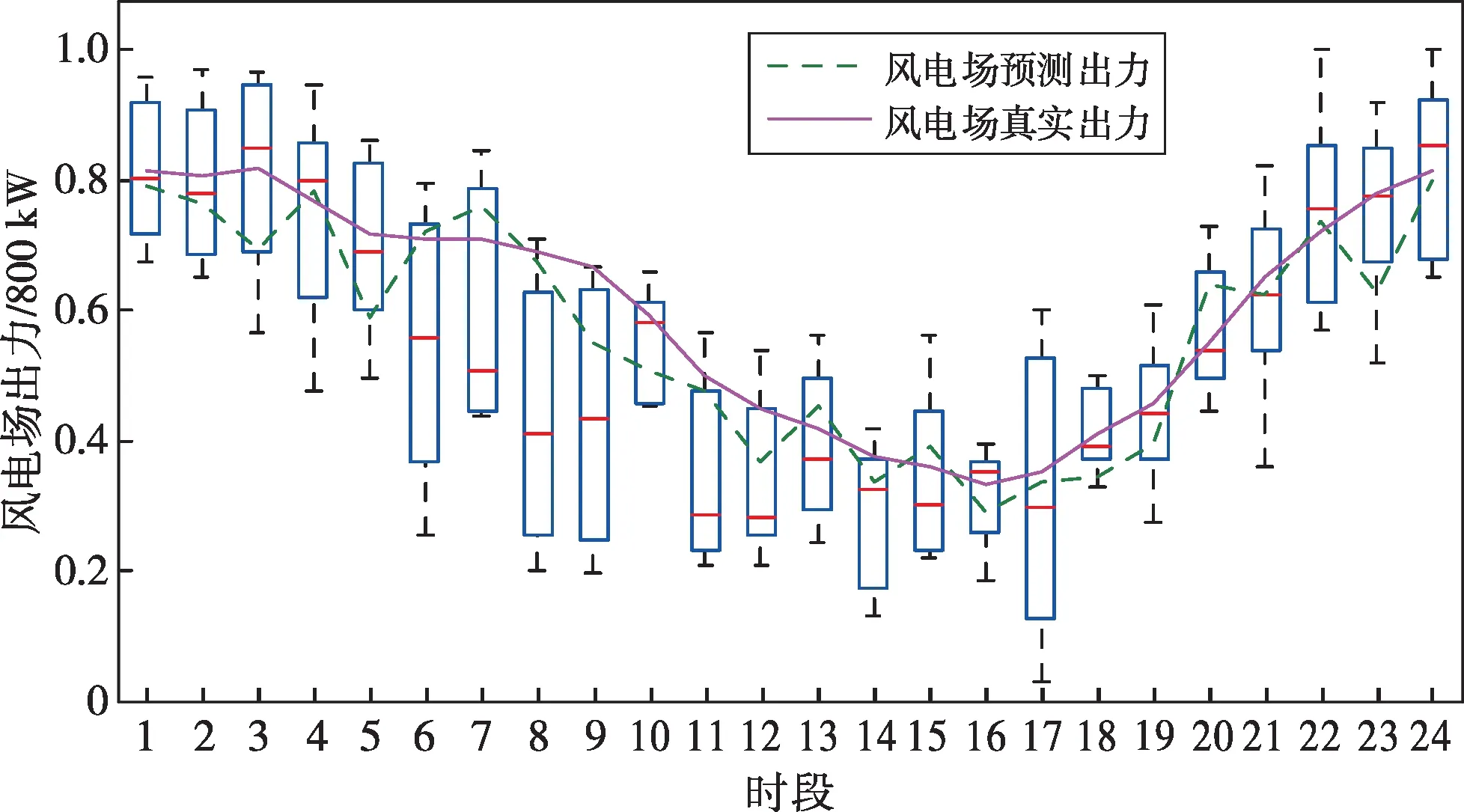
圖4 風電場誤差場景統計

5.2 優化經濟調度分析

以IEEE 33 節點多微網系統為例，家庭型微網MG1、商業性微網MG2 分別在節點28 和11 接入，如圖5所示。

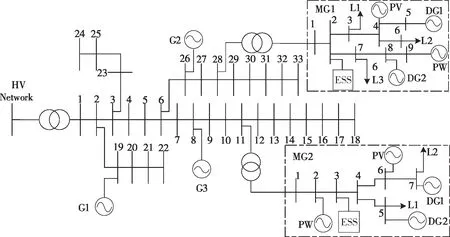
圖5 IEEE 33節點多微網系統

兩組微網日最大負荷為3 MW，均包含2 臺1.5 MW燃氣輪機、1臺0.8 MW風電機組、1組蓄電池。MG1 光伏裝機容量為0.4 MW，MG2 光伏裝機容量為0.6 MW。各微網配置情況均來源于某實際運行微網，機組參數如表2所示。配電網與各系統的分時交易電價參見文獻［15］。蓄電池充電價格為0.4 元/kWh，放電價格為0.6 元/kWh。罰函數乘子ωj和γj初值設置為1.5，收斂精度ε1和ε2取0.01，聯絡線功率初始值為0。

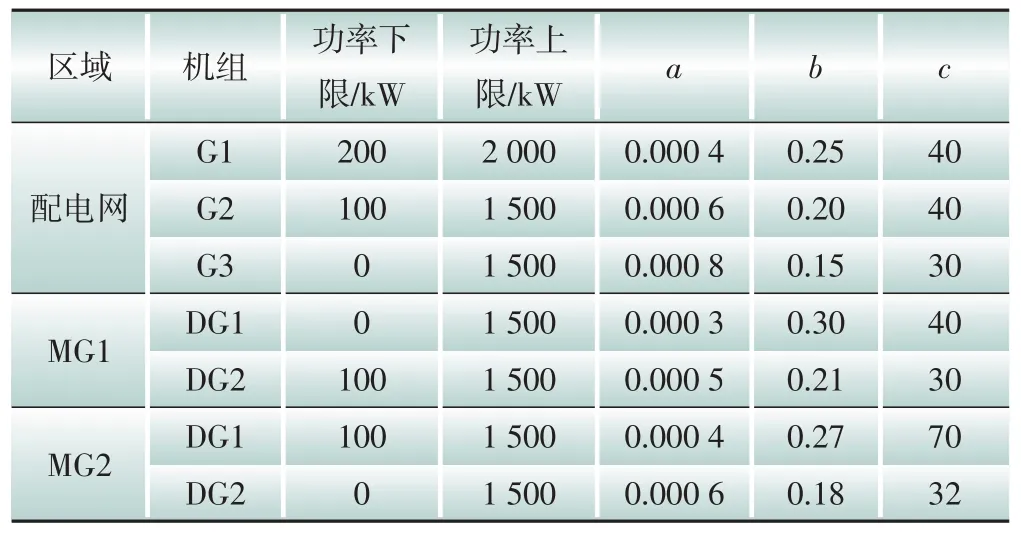
表2 多微網系統各機組參數

為驗證模型和方法的有效性，設置三種情景進行分析：

情景一：風光出力不考慮隨機性及相關性，其曲線取風光功率預測曲線，分別采用本文方法和集中式調度方法進行對比論證。

情景二：風光出力考慮隨機性及相關性，其誤差場景出力曲線由Copula函數抽樣縮減形成。

情景三：風光出力僅考慮隨機性，兩者出力獨立，參照情景二抽樣生成誤差場景（情景三為情景二Copula函數為常數1的特例）。

情景一下配電網、各微網部分機組調度結果如圖6所示。從圖6可以看出，本文模型及求解方法與集中式求解結果一致，各微網優化時獨立并行求解且具有全局收斂性。文獻［14］對ATC的算法性能進行了全面分析，本文不再贅述。

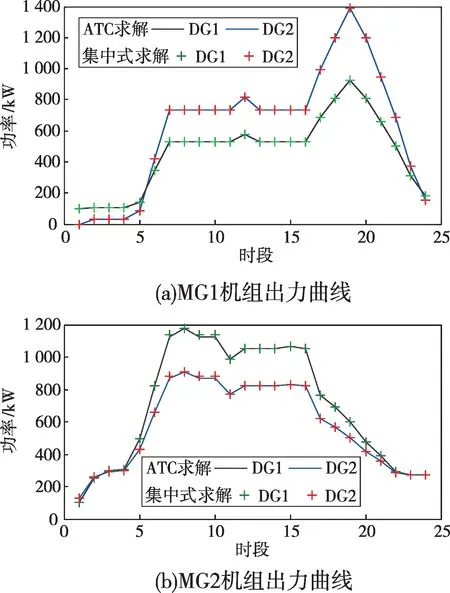
圖6 情景一下兩種求解方法的結果對比

情景二下微網各機組出力情況如圖7所示。與情景一相比，當考慮風光隨機互補特征時，各微網機組出力曲線與負荷協同趨勢減弱，呈現明顯的波動性。在該情景下，各微網調度兼顧運行的安全性與經濟性，系統不僅追求預測場景下的成本最優，而且誤差場景發生時各機組留有足夠的可調節裕度來確保系統穩定，因此機組出力需進行更多調整。

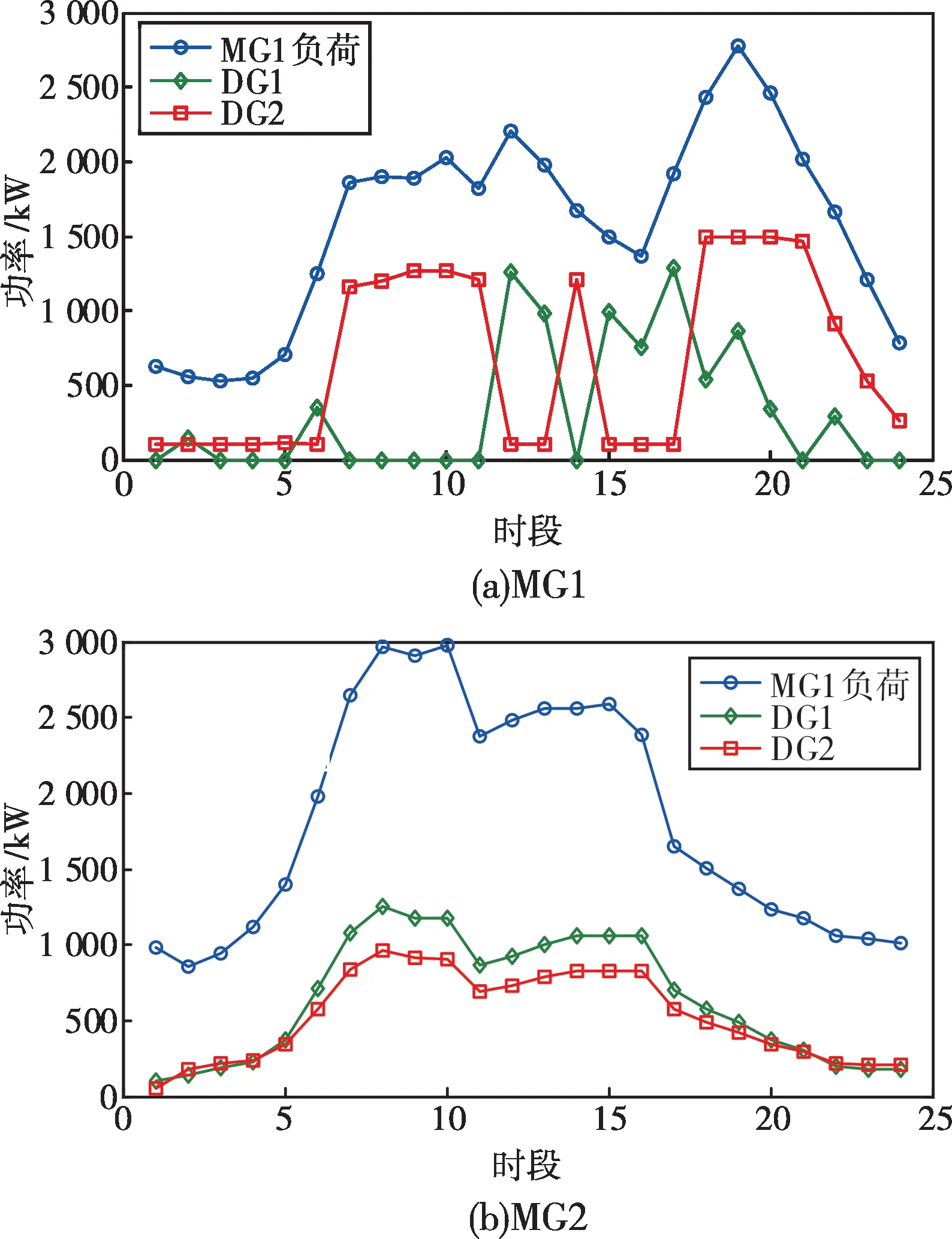
圖7 情景二下各微網機組出力情況

預測場景及誤差場景下機組出力如圖8 所示。宏觀上兩種場景下機組出力具有相同的變化趨勢，微觀上誤差場景下機組出力圍繞預測場景變化，各機組通過實時調整出力大小應對新能源的波動。圖8展現了風光隨機互補特征對微網各機組調度的影響，以及誤差場景下機組出力的變化范圍，可協助調度運行人員全面分析、制訂調度計劃。

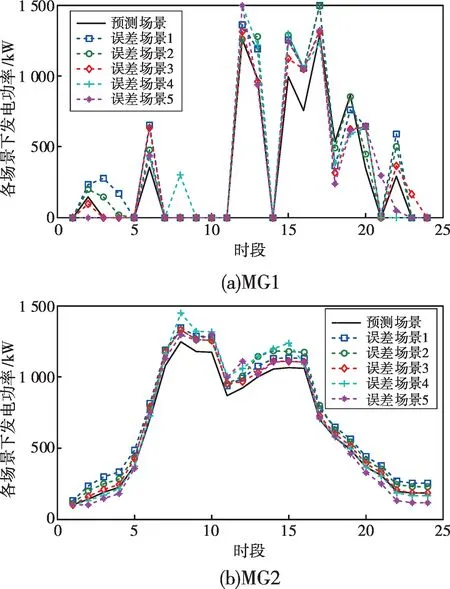
圖8 預測場景及誤差場景下機組出力曲線

為驗證風光互補特征對調度結果的影響，對情景二和情景三收益成本進行核算。根據調度當天風光電場實際出力大小求得機組的真實出力，以及不同情景下機組計劃出力與真實出力的再調度成本，如表3所示。

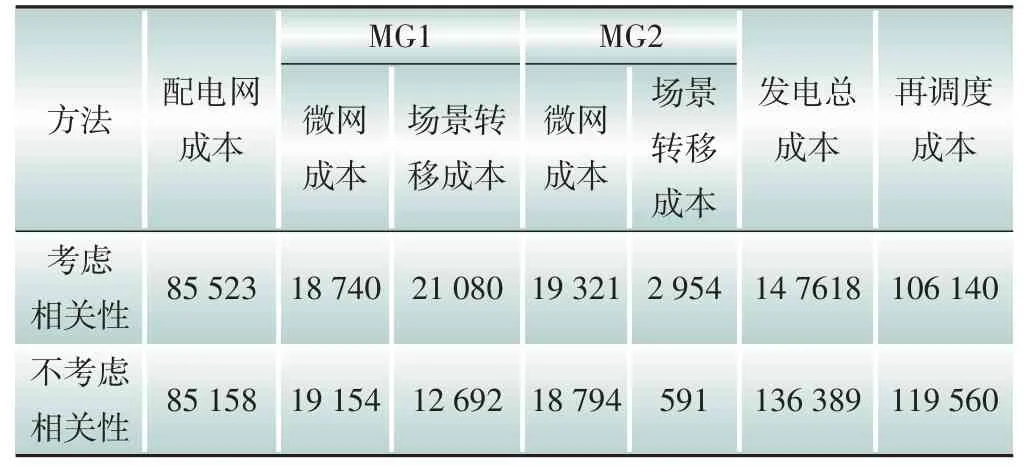
表3 考慮相關性和不考慮相關性的成本對比 元

由表3可知，考慮風光相關性時，多微網系統場景轉移費用及發電總成本均比不考慮相關性時費用高，但再調度成本較低。兩種情景下：配電網及各微網各部分費用大致相同；場景轉移費用方面，在情景二下，系統充分考慮其互補特征，兼顧風力發電充裕、光伏電站出力少的極端情況，因此其場景轉移費用及發電總成本高于情景三；再調度費用方面，考慮風光相關性時各機組已預留足額裕度應對風電滿發、光伏停發等情況，使得調度結果更符合實際情況，系統再調度成本比不考慮風光相關性時減少13 420元。

綜合發電總成本及再調度費用來看，考慮風電相關性時再調度費用大幅減少，系統總體費用降低，實現了多微網系統經濟性提升，驗證了本文模型及算法的有效性。

6 結語

本文應用Copula 理論及場景縮減技術構建考慮風光相關性的場景生成方法，基于雙層規劃理論及場景法建立多微網系統經濟調度模型，并引入ATC實現不同利益主體并行求解［16-18］。結論如下：

1）本文提出基于歷史數據和Copula 函數的風光互補場景生成步驟，建立相關性和擬合性指標的Copula模型綜合評價方法。算例分析表明風光出力呈現負相關性，經進一步對比分析，Frank-Copula較Gumbel-Copula、Clayton-Copula、Gaussian-Copula、t-Copula 擬合指標更優，函數相關性與樣本最接近。

2）本文基于雙層規劃理論及場景法構建多微網系統經濟調度模型，依托Frank-Copula 函數構建風光聯合密度函數，考慮風光出力相關性、隨機性對系統經濟調度的影響。將ATC 應用于上、下層模型并行求解，降低信息交互度，且與集中式求解方法結果一致。

3）本文對IEEE 33 節點系統算例進行分析，考慮風光相關性時再調度費用減少11.2%，系統總成本降低。且考慮風光相關性時各機組已預留足額裕度應對風電滿發、光伏停發等情況，在極端場景時能靈活調整機組出力，提升系統的安全性。

本文分析風光互補特征對多微網系統經濟性、安全性的影響，但模型僅考慮了配電網與微網的相互作用，未考慮微網間的協同互濟、互為備用，未體現電力市場環境下電價彈性機制、可中斷彈性負荷對模型的影響，未分析多種分布式能源間（如相鄰風電場之間）的相關性。后續將研究配電網-多微網-需求側負荷多層次的協調模型，分析多種分布式能源的相關性，提升新能源消納水平［19-21］。