基于Kalman濾波的改進灰色模型在基坑變形監測中的應用

劉國超，彭衛平，朱曉強

(1.廣州市城市規劃勘測設計研究院，廣東 廣州 510060； 2.廣東省城市感知與監測預警企業重點實驗室，廣東 廣州 510060)

1 引 言

隨著城市化進程的快速推進，大城市人口規模的快速增加，使得城市土地愈發緊張，建筑設計向上要空間，使得樓層越來越高，基坑越挖越深，建筑規模越來越大，隨之而來的工程沉降、工程塌陷問題愈發突出。高層建筑一般位于城市核心地帶，基坑規模大，周邊環境復雜，施工引起的沉降問題不容忽視，如果發生險情可能引發投資增加、工程安全或人員傷亡等一系列問題。基坑監測作為驗證基坑設計、保護基坑施工的主要手段，可以直觀反映基坑在各種施工工況、巖土體卸荷載狀態下的變化情況，通過對監測數據的分析和預測，可以為后續設計和施工提供有益指導[1]。

基坑監測數據由于其離散性、高噪聲等特點，使得監測數據呈現一定的波動性、隨機性，為了對基坑的穩定狀態及變形趨勢做出更加準確的分析，國內外學者做了很多有益嘗試。文獻2中介紹了新陳代謝GM(1，1)模型在建筑物沉降數據預測中的應用，相比于傳統的GM(1，1)模型和多項式擬合模型，精度提高明顯[2]；文獻3中建立了基于卡爾曼濾波的灰色理論預測模型，利用迭代濾波理論和LevenbergMarquardt優化濾波，有效提高了預測精度[3]；文獻4中系統闡述了自適應卡爾曼濾波在變形監測數據處理中的應用，并探討了不同自適應卡爾曼濾波模型的不同應用領域[4]；文獻5中詳細討論了離散線性系統的卡爾曼濾波模型建立及精度評定，并將其應用于大壩動態變形監測中[5]。以上探索和嘗試，為變形監測分析和預測提供了豐富工具，本文擬采用Kalman濾波+新陳代謝GM(1，1)模型組合方式，利用Kalman濾波對原始監測數據濾波消噪，并結合新陳代謝GM(1，1)模型對變形趨勢項進行建模分析，來預測變形趨勢。結合實際案例分析，基于Kalman濾波的新陳代謝GM(1，1)相比于傳統的單一GM(1，1)、ARMA模型[6-7]，有效降低了觀測噪聲影響，并具有更高的預測精度。

2 基于Kalman濾波的新陳代謝GM(1，1)模型

2.1 Kalman濾波模型

Kalman濾波是一種利用線性系統狀態方程，對系統狀態進行最優估計的一種算法，能有效剔除測量數據中隨機擾動誤差，得到接近真實情況的測量數據。其數學模型包括狀態方程(也稱動態方程)和觀測方程兩部分：

Xk=Φk/k-1Xk-1+Wk-1

(1)

Lk=HkXk+Vk

(2)

式中，Xk是tk時刻系統的狀態向量；Lk為tk時刻系統的觀測向量；Φk/k-1為時間tk-1至tk的系統狀態轉移矩陣；Wk-1為tk-1時刻的動態噪聲；Hk為tk時刻的觀測矩陣；Vk為tk時刻的觀測噪聲。

離散的線性系統Kalman濾波遞推公式為：

狀態預報：

(3)

狀態協方差陣預報：

Pk/k-1=Φk/k-1Pk-1+Qk-1

(4)

狀態估計：

(5)

狀態協方差陣估計：

Pk=(I-KkHk)Pk/k-1(6)

其中，Kk為濾波增益矩陣，其具體形式為

(7)

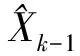
2.2 GM(1，1)模型

灰色模型是通過少量的、不完全的信息，建立數學模型并做出預測的一種方法，是黑箱概念的推廣，通過分析系統各因素之間是否具有確定關系來區別白色與黑色系統，進而建立數學模型，并做出預測。

設觀測原始序列：

x(0)={x(0)(1)，x(0)(2)，x(0)(3)，…，x(0)(N)}

對x(0)作一次累加生成(1-AGO)，得到：

(8)

從而獲得生成序列：

x(1)={x(1)(1)，x(1)(2)，x(1)(3)，…，x(1)(N)}

設x(1)滿足：

(9)

其中，常數u稱為發展灰數，a為內生控制灰數，是對系統的常定輸入。通過最小二乘估計可得：

(10)

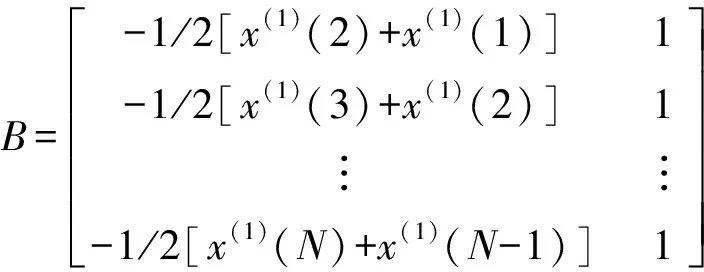
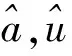
(11)

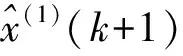
2.3 Kalman濾波與GM(1，1)模型組合及算法實現

Kalman濾波能有效剔除測量數據的隨機項，得到接近真實情況的測量數據；新陳代謝GM(1，1)模型可以對監測數據趨勢項進行建模，以預測變形趨勢。本文擬采用Kalman濾波+新陳代謝GM(1，1)模型組合方式，利用Kalman濾波對原始監測數據濾波消噪，并結合新陳代謝GM(1，1)模型對變形趨勢項進行建模分析，來預測變形趨勢。

首先采用Kalman濾波對監測數據進行濾波，剔除監測數據中的隨機擾動誤差，然后對剔除了隨機項的監測數據進行GM(1，1)建模。針對灰色系統隨時間推移，預測精度與可靠度不斷下降的問題，本文擬通過將已經獲取的最新已知信息引入模型，淘汰作用弱的信息，淡化灰平面的灰度，以降低模型精度的損失，準確反映系統狀態。

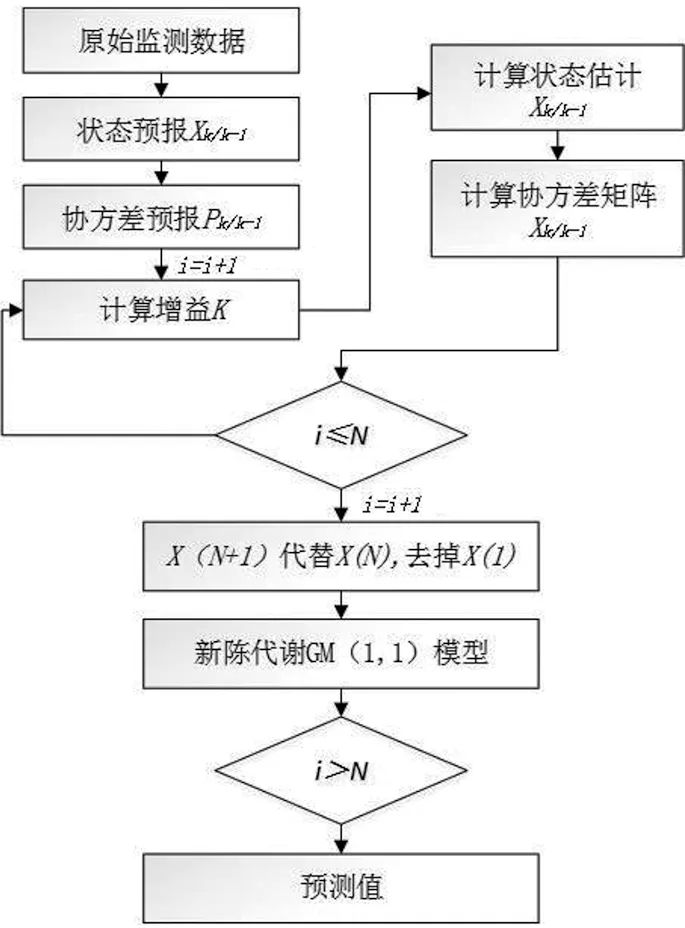
圖1 基于Kalman濾波的改進灰色模型算法流程

3 算例分析

廣州城區某高層建筑，基坑周長約 600 m，開挖深度 16 m，基坑等級為一級。為監測基坑施工過程中的變形情況及周邊影響，在基坑及周邊建筑布設若干監測點，本文選取基坑樁頂某豎向位移監測點14期數據作為實驗數據，通過前10期數據建立模型，預測后4期數據，并與實際監測數據對比，其中每期監測間隔為7天，監測數據如表1所示。

表1 某監測點部分沉降數據

這里選取前4個數據為觀測值，定△t=1，組成法方程進行動態平差，采用線性擬合y=a0+a1x+ε，得到狀態協方差陣和狀態估計參數。利用上面的遞推預報與濾波公式可得到監測點的濾波值，如表2所示：

由表2可知，卡爾曼濾波通過建立狀態方程和觀測方程來描述系統的動態過程，依據濾波增益矩陣的變化，從監測數據中定量提取有效信息，修正狀態參量，從而補償噪聲對數據的影響，有效提高數據處理精度。以濾波值為基礎，建立新陳代謝GM(1，1)模型，并預測后4期數據，并分別對于傳統GM(1，1)模型、ARMA模型進行對比，結果如表3所示。

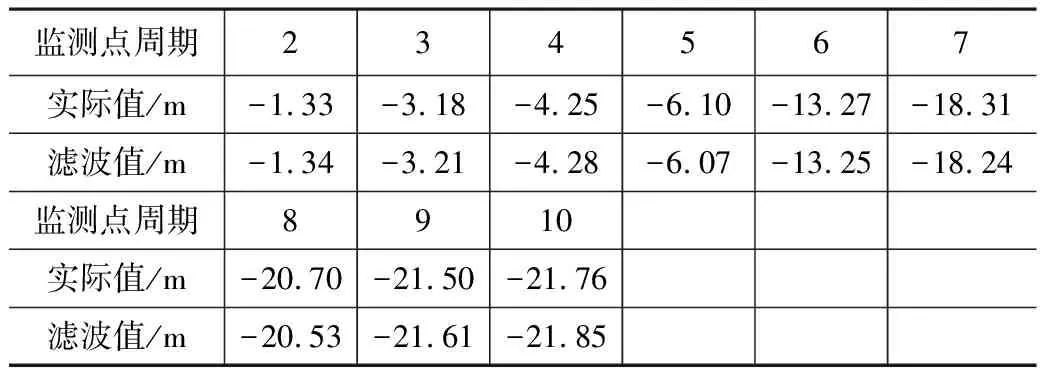
表2 Kalman濾波值與預測值

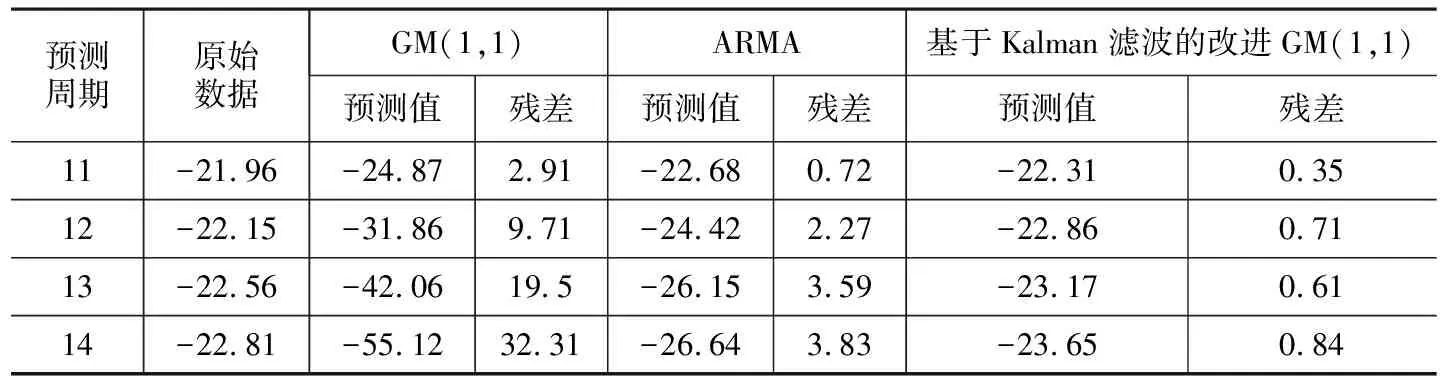
表3 基于Kalman濾波的改進GM(1，1)與傳統GM(1，1)、ARMA預測值比較

由表3，圖2可知，經卡爾曼濾波處理后的改進GM(1，1)模型具有更高的預測精度，能更好地反映變形趨勢，相比于單純GM(1，1)模型和ARMA模型精度更高。

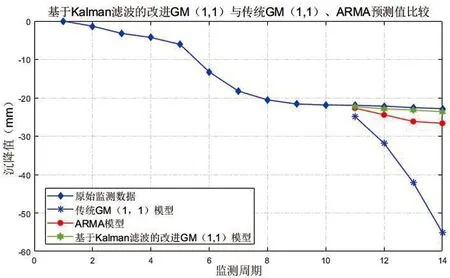
圖2 基于Kalman濾波的改進GM(1，1)與傳統GM(1，1)、ARMA預測值比較

由表4可知，對比三種模型的預測值、殘差值的均方差及中誤差，基于Kalman濾波的新陳代謝GM(1，1)相比于傳統的單一GM(1，1)、ARMA模型，有效降低了觀測噪聲影響，并具有更高的預測精度。

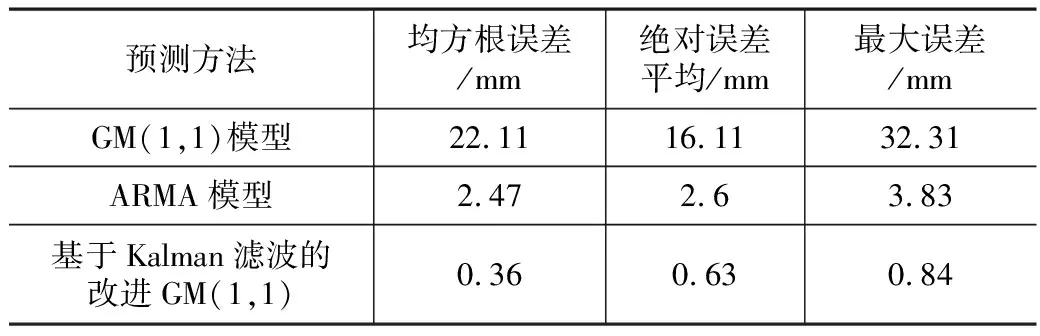
表4 三種模型預測精度對比

4 結 論

卡爾曼濾波通過建立狀態方程和觀測方程來描述系統的動態過程，依據濾波增益矩陣的變化，從監測數據中定量提取有效信息，修正狀態參量，從而補償噪聲對數據的影響，有效地提高數據處理精度，結合新陳代謝GM(1，1)模型對變形趨勢項進行建模分析，來預測變形趨勢。相比于傳統的單一GM(1，1)、ARMA模型，有效降低了觀測噪聲影響，并具有更高的預測精度。但是在使用上述模型時，也要注意以下幾點：

(1)Kalman濾波初始值的選取很關鍵，錯誤的初始值不能很好反映數據變化趨勢；

(2)Kalman濾波的優勢在于能實時反映數據變化狀態，并通過新數據來更新狀態方程，通過增益矩陣來控制觀察數據噪聲的影響，對提高數據預測精度有很好的效果；

(3)新陳代謝的GM(1，1)模型通過加入新的已知信息，剔除舊的無效信息，來提高預測精度，但也易受到突變信息、粗差信息干擾，導致預測不準。使用模型時，需對新加入的數據做一定的判別和分析。