一種優化直流接觸器電動斥力的改進方法

夏 林, 遲長春, 陳晉生

(上海電機學院 電氣學院, 上海 201306)

隨著可再生能源投入使用比例增加、電動汽車市場占比上升,人們對直流電氣設備的需求逐步增加[1-3]。因此,直流接觸器的安全性和可靠性越來越受到研究人員的關注。直流接觸器導體回路的電動斥力由導體間的電動力和觸點之間的霍爾姆力組成[4]。在短路電流故障下,電動斥力會使得觸頭回路斷開。觸頭自動斷開后產生的強大電弧會使觸頭表面熔化和汽化,最終導致觸頭材料或觸頭熔焊[5]。同時,直流接觸器的突然斷開也會影響電路中其他設備的運行。

對電動斥力的優化一直是電器領域的研究熱點。國內學者對斷路器、繼電器的電動斥力及其影響因素做了大量研究[6-9],但是針對直流接觸器電動斥力的研究很少。李興文等[10]研究了長方形觸頭導電橋的位置對電動斥力的影響,但是沒有分析圓形觸頭導電橋的位置對電動斥力的影響。對于電動斥力的優化,許多學者采用改變觸頭結構的方式[11-14]。董華軍等[15]在真空滅弧室的觸頭之中添加不同形狀的環形隔磁塊DT4,有效地減小了觸動間的電動斥力。陳晉生等[16]則通過添加方形隔磁塊的方式優化電動斥力,但沒有討論隔磁塊厚度對電動斥力的影響。

處在磁場中的隔磁塊能夠產生與該磁場相反的磁場,可以削弱磁場,進而減小電動斥力。本文將用于電動汽車充電樁、充電站領域的NDZ3T-400/750 V直流接觸器作為研究對象,利用電磁仿真軟件ANSYS對其觸頭系統在不同短路電流下產生的電動斥力進行研究。仿真結果發現,導電橋在不同位置時的電動斥力不同;當電流小于4 k A時選取厚度為1.5 mm 的方形隔磁塊較為合適,當電流大于4 k A 則選擇厚度為4 mm 的方形隔磁塊;厚度相同的情況下,U 形隔磁塊的優化效果要明顯強于方形隔磁塊。

1 觸頭系統電動斥力的數學模型和仿真

1.1 直流接觸器的電動斥力

直流接觸器可以通過控制線圈電流的通斷,使得聯動機構帶動觸頭運動,進而控制電路的通斷,其主要由動鐵芯、靜鐵芯、線圈、動觸頭、靜觸頭等組成,如圖1所示。線圈通電后,動觸頭和靜觸頭接觸,當直流接觸器控制的電路短路時,動觸頭、靜觸頭以及動觸板上的磁場強度會激增,進而導體回路的電動斥力也會大幅增加。在動觸板上的平面上可以放置削弱磁場的隔磁塊,從而降低電動斥力。

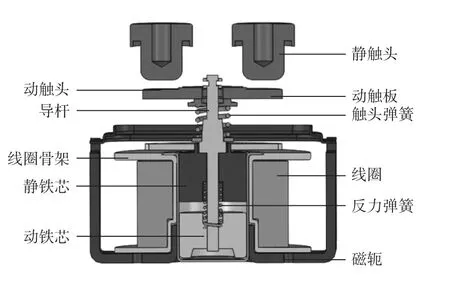
圖1 直流接觸器的結構

導體回路垂直方向的電動斥力FC由導體間的電動力FL和觸點之間的霍爾姆力FH組成。工程上通常采用比奧 沙伐定理計算電動力。可將觸頭系統中的各個導體看作處于同一平面上,則電動力計算公式為

式中:μ0 為空氣磁導率,μ0=4π×0.1μH/m;I為流過觸頭系統的電流;Kh為回路系數,與載流導體的長度、導體間的相互位置、導體間的介質有關,不同的情形下,回路系數會不同。

將觸頭機構的回路導體簡化為兩個互相平行的導體并垂直于另一條導體的結構。對于兩個互相垂直的有限長載流導體,回路系數表達式為

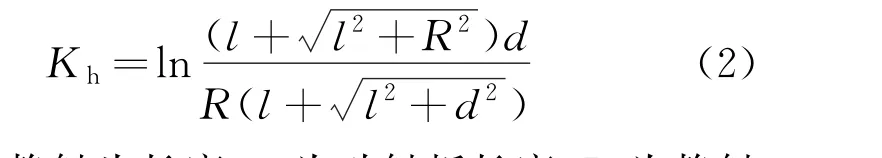
式中:l為靜觸頭長度;d為動觸板長度;R為靜觸頭的半徑。

本文接觸器l=115 mm,d=25.5 mm,R=5.5 mm,由于R?l,則Kh簡化為

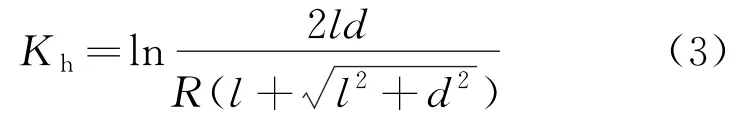
簡化的觸頭系統中電流流入的觸頭和動觸板為互相垂直的兩個導體,電流流出的觸頭和動觸板也是互相垂直的兩個導體,水平導體受到的總電動力為

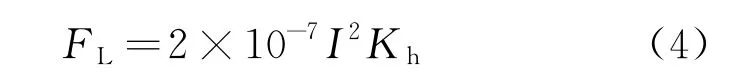
由于在觸點附近,電流線收縮,上下兩個觸頭之間會產生相反的電動力,簡稱為霍爾姆力。兩對動靜觸頭之間受到的霍爾姆力計算公式如下[17]:

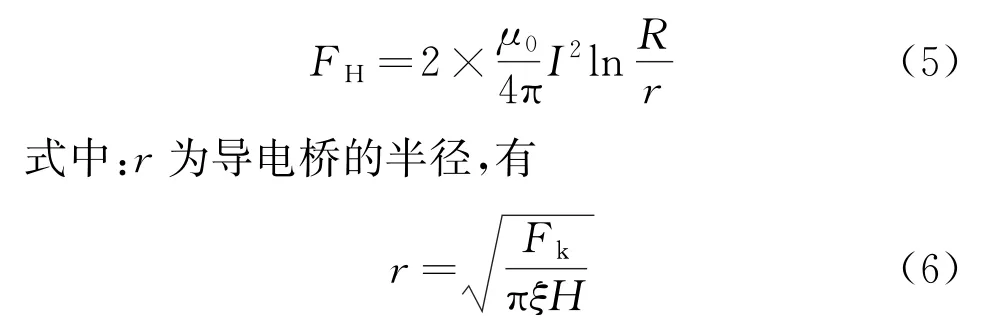
式中:Fk為觸頭間的預壓縮力;H為觸頭材料的布氏硬度;ξ為觸頭表面的粗糙程度,通常情況下取ξ=0.45。

通過公式求得r=0.26 mm。

1.2 隔磁塊工作原理簡介

隔磁塊被磁化時,磁化強度表達式為

式中:Δv為磁化物質的微小單元的體積;Δm為微小部分中磁化電流的磁矩。

當隔磁塊處于磁場H0之中時,會產生相應的附加磁場H′,其表示如下:

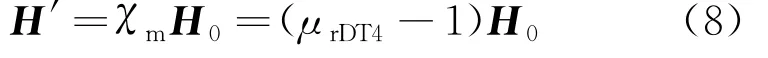
式中:χm為磁化率;μrDT4 為DT4的相對磁導率。

附加磁場的方向與外部磁場的方向相反,從而削弱了隔磁塊附近的磁場。隔磁塊周圍的磁場表達式為

此時磁感應強度表達式為

式中:μr 為導電介質的相對磁導率。

利用隔磁塊削弱觸頭系統的磁場強度,從而降低導體回路所受的電動斥力。通過改變隔磁塊的厚度和形狀,確定不同參數下的隔磁塊對電動斥力的影響。

1.3 觸頭系統的有限元建模

在ANSYS軟件中建立直流接觸器的觸頭系統,模型如圖2(a)所示,其中隔磁塊放置在動觸板的中間。對動靜觸頭之間的導電橋單獨建模,如圖2(b)所示。假設導電橋是半徑為r的圓形區域,R為靜觸頭的半徑。一般導電橋的厚度在0.10～0.25 mm,這里取厚度為0.15 mm[18]。

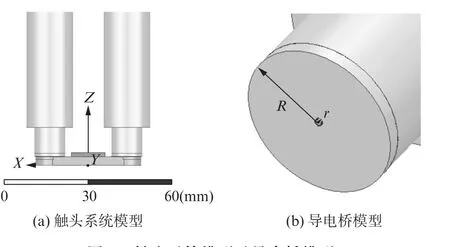
圖2 觸頭系統模型及導電橋模型

設定該直流接觸器的動靜觸頭、導電橋等參與導電的材料為銅,放置在動觸板上的隔磁塊材料為DT4。模型搭建完成后,設置計算邊界為零切線磁場強度場,并在觸頭表面施加短路電流激勵。劃分模型網格后,在動觸板上設定求解參數,即動觸板所受的電動斥力,求解后得到仿真結果。

2 仿真結果與分析

2.1 模型仿真計算驗證

為了確保模型的可靠性,對直流接觸器的觸頭系統在不同短路電流下的電流電動斥力進行理論計算,并與實際的有限元仿真結果對比,結果如圖3所示。

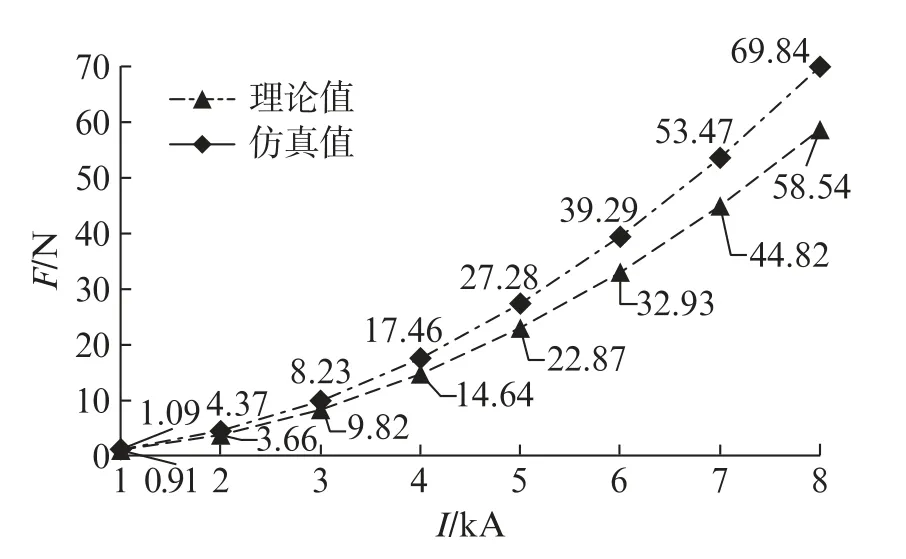
圖3 電動斥力(F)的理論值和仿真值對比

由圖3可知,總體上看,理論值和仿真值的計算結果相近,當短路電流變大后,理論值和仿真值的差異逐漸增大,這是因為理論計算結果是根據接觸器的觸頭系統簡化后得來的,只能大致體現電動斥力的變化,而有限元則是對實際的觸頭系統進行建模,計算結果更加準確。

2.2 導電橋所在位置對電動斥力的影響

假設每個靜觸頭上只存在一個導電橋,按照圖4中位置1～7號分別放置,其中4號位置處于觸頭的圓心,剩余的位置沿X軸分布在距離4號±1 mm,±2.5 mm,±4 mm 的位置。由于市場上直流接觸器的短時耐受電流最高為8 k A,故限定仿真中短路電流最高為8 k A。設置短路電流I=8 k A,則電動斥力的結果如表1所示。

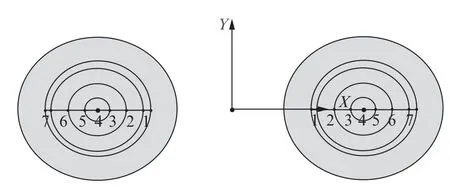
圖4 導電橋位置分布

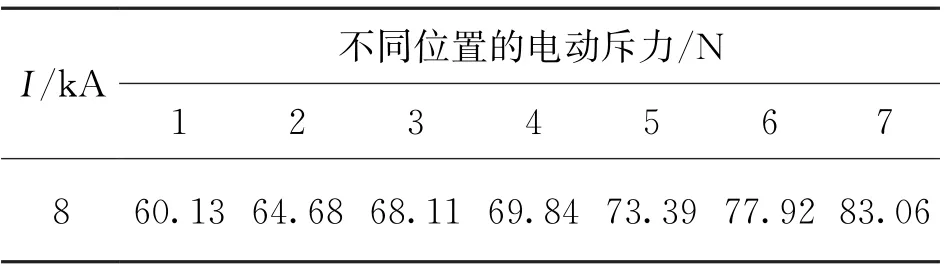
表1 不同位置導電橋的電動斥力

由表1可知,離動觸板中心越近,觸頭系統的電動斥力就越小,反之越大。位置1的電動斥力最小,位置7的電動斥力最大。

2.3 不同位置下方形隔磁塊對電動斥力的影響

將12 mm×12 mm×1 mm 的方形隔磁塊放置在動觸板上,隔磁塊的中心和動觸板的中心重合。設降幅比例的計算公式為

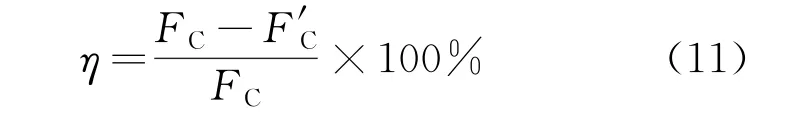
式中:FC為不放置隔磁塊的電動斥力;F′C為放置隔磁塊后的電動斥力。

電流為2、4、6和8 k A 時,仿真結果以及相應降幅比例計算如表2所示。

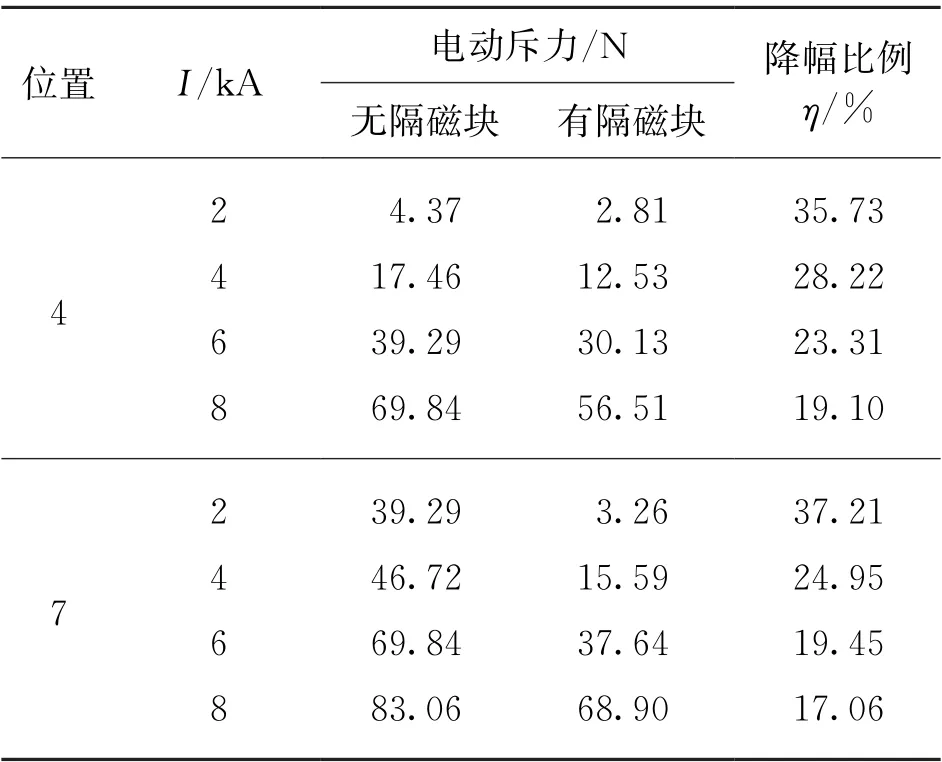
表2 不同位置下方形隔磁塊對電動斥力的降幅比例

由表2可知,當導電橋處于位置4或者7時,方形隔磁塊在不同的短路電流下都能一定程度上減小電動斥力。在相同短路電流下,不同位置的降幅比相差小于5%,且降幅趨勢相同。因此,為了便于仿真,選擇處于位置4的導電橋模型進行仿真。

2.4 不同厚度的隔磁塊對電動斥力的影響

改變方形隔磁塊厚度h從1.0～4.5 mm,間隔為0.5 mm,仿真數據如表3所示。由表可知,短路電流不變的情況下,隨著隔磁塊厚度的增加,電動斥力也有所下降,但是下降的趨勢越來越平緩。考慮到觸頭的壓力為30 N,當短路電流小于4 k A時,無論選擇哪一種厚度的隔磁塊都能減小電動斥力。

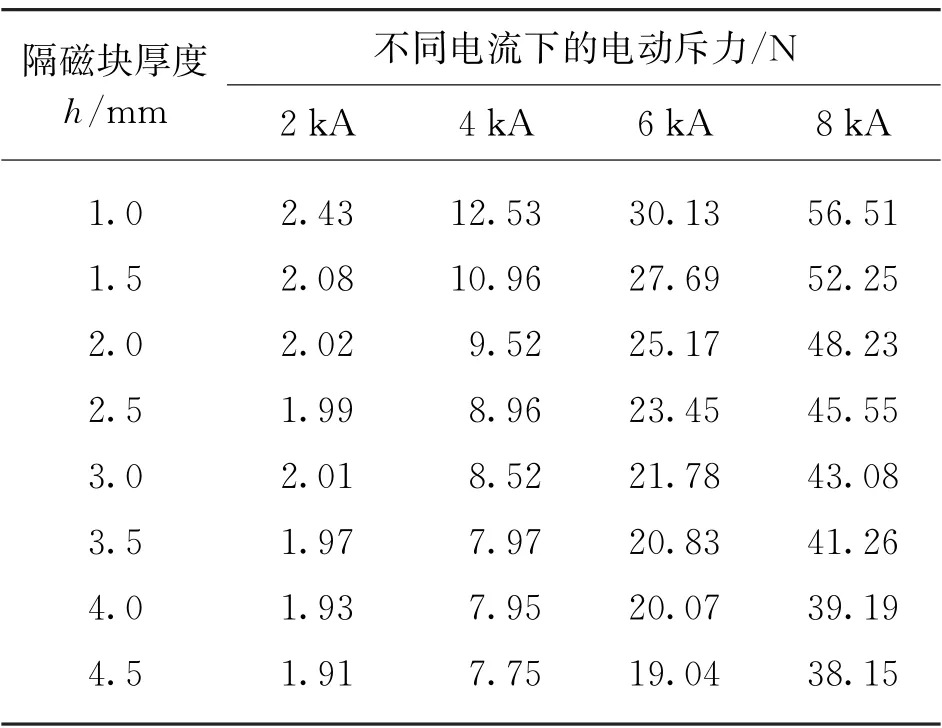
表3 不同厚度、不同電流下的方形隔磁塊的電動斥力

設降幅變化率為

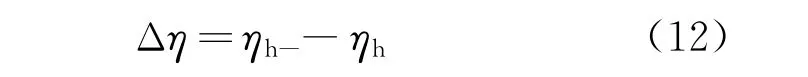
式中:ηh-為沒有增加0.5 mm 隔磁塊時對應的電動斥力降幅比例;ηh 為當前隔磁塊厚度下的電動斥力降幅比例。

特別地,當h=1 mm 時,取Δη=ηh,對應的電動斥力降幅變化率曲線如圖5所示。

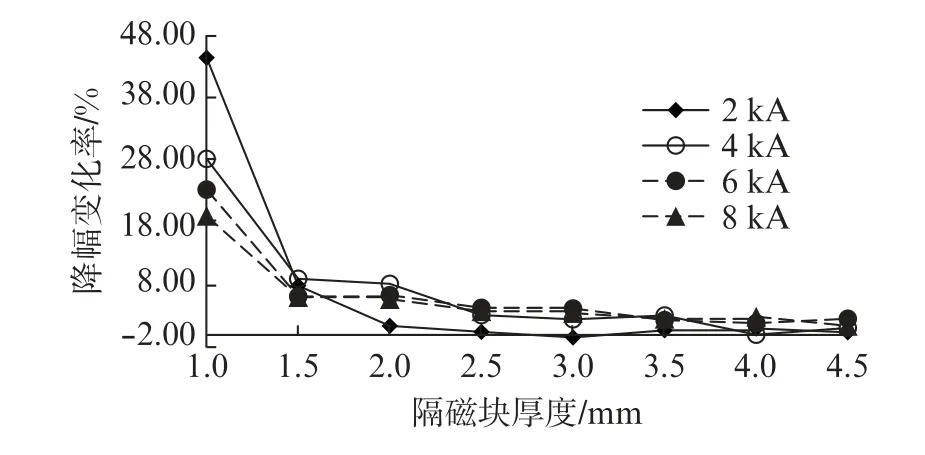
圖5 不同厚度的方形隔磁塊的電動斥力降幅變化率

由圖5可知,當短路電流小于4 k A時,厚度大于1.5 mm 的隔磁塊降幅的效果趨于平緩,即隔磁塊的厚度再增加也不會有明顯的電動斥力優化效果,故選擇厚度為1.5 mm 的隔磁塊較為合適。同理,當短路電流大于4 k A 時,隔磁塊越厚,電動斥力越小,但是當厚度達到4 mm 后,電動斥力下降的趨勢越來越平緩。因此,當短路電流大于4 k A時,選擇厚度為4 mm 的隔磁塊較為合適。

2.5 U形隔磁塊對電動斥力的影響

為了解決方形隔磁塊隨著厚度增加,電動斥力不再明顯的問題,對隔磁塊進行改造。由于動觸板中心的磁場強度相對較小,而越靠近動觸板邊緣以及導電橋的位置時,磁場強度越大。根據動觸板磁場強度的分布,設計U 型隔磁塊,如圖6所示,覆蓋動觸板的邊緣。

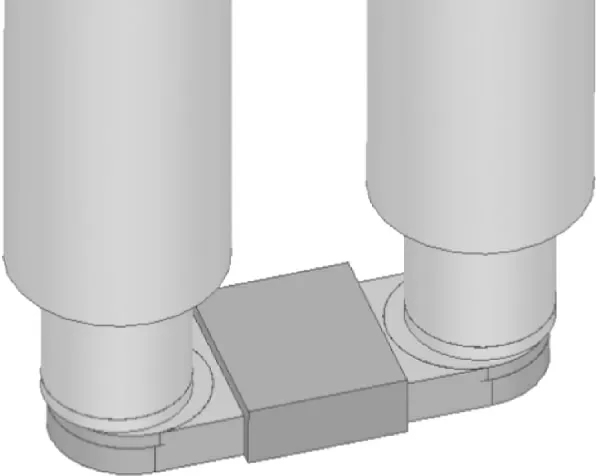
圖6 U形隔磁塊擺放示意圖

確定短路電流小于4 k A、厚度h=1.5 mm 與短路電流大于4 k A、厚度h=4 mm 的U 型隔磁塊對電動斥力的仿真效果,仿真結果如表4所示。

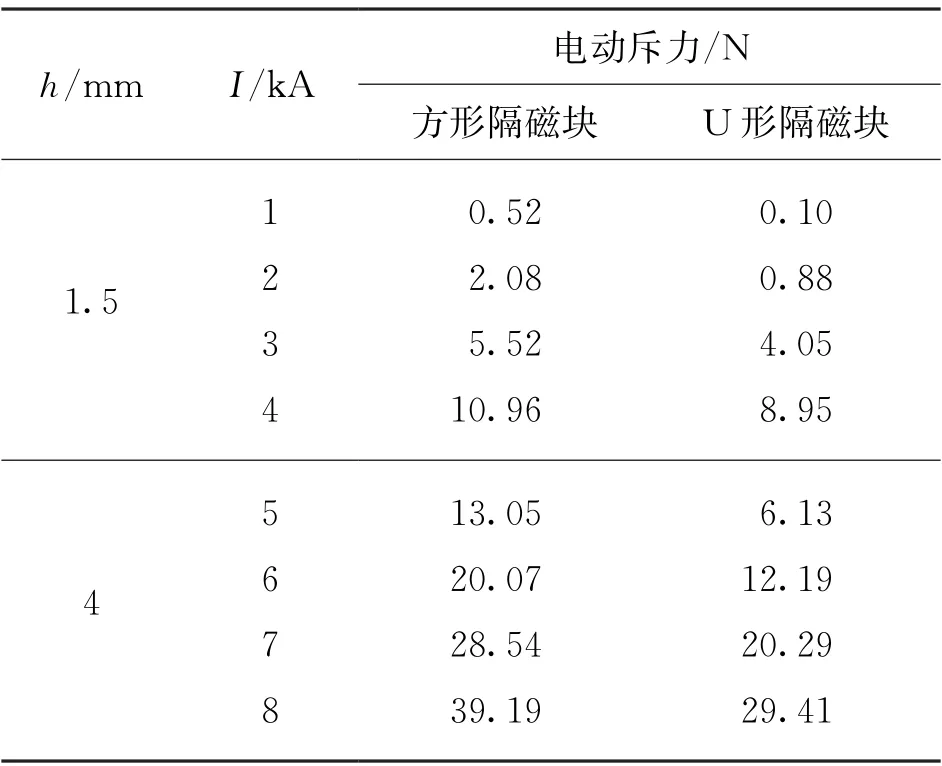
表4 不同條件下方形隔磁塊和U形隔磁塊的電動斥力

結合圖3中的仿真值,計算方形隔磁塊和U形隔磁塊在不同條件下對電動斥力的降幅比例,計算結果如圖7所示。

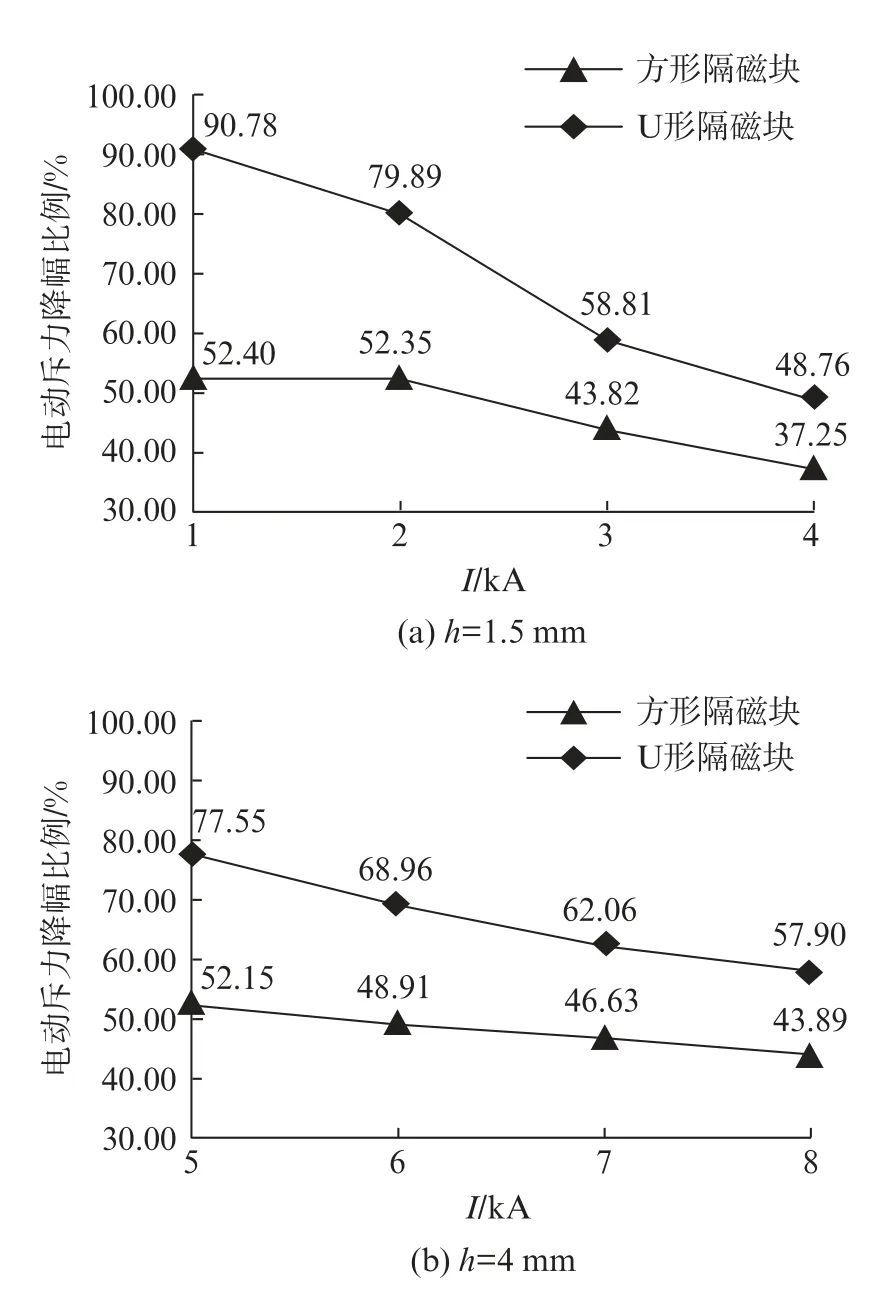
圖7 不同厚度下方形和U形隔磁塊的降幅比例

由圖7可知,當電流小于4 k A 時,1.5 mm 的U 型隔磁塊的優化效果比1.5 mm 的方形隔磁塊更優,并且U 型隔磁塊的降幅比例至少比方形隔磁塊的降幅比例多11.51%;當電流大于4 k A 時,4 mm 的U 型隔磁塊的優化效果要強于4 mm 的方形隔磁塊,并且U 型隔磁塊的降幅比例至少比方形隔磁塊的降幅比例多14.01%。

3 結 語

本文對直流接觸器的觸頭系統進行了仿真,在ANSYS之中建立觸頭系統的Maxwell 3D 模型。改變了靜觸頭上導電橋的位置,發現導電橋離動觸板中心越遠,觸頭系統的電動斥力就越強。當短路電流小于4 k A 時,選擇厚度為1.5 mm 的方形隔磁塊可以取得較好的電動斥力優化效果;當短路電流大于4 k A 時,則選擇厚度為4 mm 的方形隔磁塊。在隔磁塊厚度相同,短路電流相同的條件下,U 形隔磁塊的優化效果要強于方形隔磁塊,且電動斥力的降幅比例至少比方形隔磁塊的降幅比例多10%。本文通過研究隔磁塊厚度和形狀,提高了直流接觸器的短時電流耐受能力,增強了直流接觸器在短路電路下的安全性和可靠性,為后續相同類型更大容量的直流接觸器的電動力穩定性優化研究提供了參考依據。