基于遺傳算法的護理機器人逆運動學(xué)求解方法

張立博 李宇鵬 朱德明 付永領(lǐng)

(北京航空航天大學(xué) 機械工程及自動化學(xué)院, 北京 100083)

由于全球老齡化日益嚴(yán)重,未來老年人的護理問題變得十分嚴(yán)峻,隨著現(xiàn)階段人工智能技術(shù)的發(fā)展,護理機器人投入醫(yī)療護理領(lǐng)域,可以減輕護理人員負擔(dān),提高護理人員的工作效率,一定程度上可以解決護理對象的自理能力[1]。 護理任務(wù)中,護理機器人工作需要雙臂和腰部的協(xié)調(diào)操作才能將病人抱舉,而且所處的環(huán)境一般比較復(fù)雜,抱起沉重的病人很容易發(fā)生二次傷害[2]。

護理機器人系統(tǒng)存在著多變量、強耦合、高階及非線性等特性,這些特性使得對護理機器人的逆運動學(xué)精確求解變得非常困難[3],特殊的結(jié)構(gòu)沒有非常滿意的傳統(tǒng)解法,各種算法根據(jù)自身的特點去解決特定結(jié)構(gòu)形式的機器人[4-5]。 對于串聯(lián)機器人來說逆運動學(xué)解比較復(fù)雜,根據(jù)結(jié)構(gòu)的復(fù)雜程度不同求解難度也不同,基本原理都是根據(jù)結(jié)構(gòu)參數(shù),由機械臂末端位姿矩陣求解各關(guān)節(jié)的轉(zhuǎn)動角度值[6-7]。 特定的結(jié)構(gòu)可以采用現(xiàn)有方法直接求解,如三軸交于一點的結(jié)構(gòu)一般用PIEPER 法進行研究[8-9]。 Pieper[10]證明了當(dāng)機器人有3 個相鄰關(guān)節(jié)軸相交于一點時,一定存在解析形式的逆解。 Duffy[11]證明了當(dāng)3 個相鄰的關(guān)節(jié)軸互相平行時,也一定存在解析形式的解。Goldenberg 等[12]提出了一種基于新的快速收斂約束非線性優(yōu)化算法,適用于任意自由度的旋轉(zhuǎn)或棱柱關(guān)節(jié)機器人。 Ayusawa 和Nakamura[13]提出了一種快速逆運動學(xué)算法,先將殘差視為外力并分布到每個環(huán)節(jié)再利用牛頓-歐拉遞推算法從靜態(tài)平衡點計算梯度。 Manocha 和Canny[14]提出了一種通用六自由度機械臂的高效逆運動學(xué)算法及其實現(xiàn),利用系統(tǒng)的代數(shù)性質(zhì)通過降階來計算特征值問題。 護理機器人結(jié)構(gòu)復(fù)雜,而且大小臂軸線相錯,幾何結(jié)構(gòu)不滿足PIEPER 準(zhǔn)則,代數(shù)法和幾何法不能很好解決逆運動學(xué)解問題。 遺傳算法的隱含并行性,讓其在搜索過程中具有實時性,從而能夠快速地找到合適的解[15]。 針對遺傳算法在實際應(yīng)用中出現(xiàn)早熟收斂和局部搜索能力較弱的缺點,文獻[16]在簡單遺傳算法的基礎(chǔ)上改進了交叉變異算子,改進了適應(yīng)度函數(shù)排序方法;文獻[17]通過改進交叉、變異算子自整定策略和精英策略,提高了算法的收斂速度;文獻[18]通過優(yōu)化選擇算子和變異算子提高了算法搜索速度并保證全局最優(yōu)性,具有更快的搜索速度和全局最優(yōu)性。

為了解決護理機器人手臂末端位姿誤差較大的問題,本文在分析結(jié)構(gòu)約束關(guān)系的基礎(chǔ)上,基于遺傳算法提出了護理機器的腰臂耦合逆解算法,對解進行了合理的規(guī)劃,使求解過程更為精確。

1 正向運動學(xué)分析

護理機器人正向運動學(xué)分析是遺傳算法求解逆運動學(xué)的基礎(chǔ),需要依據(jù)正運動學(xué)和機器人末端位姿坐標(biāo)系對逆運動學(xué)進行求解。

1.1 護理機器人結(jié)構(gòu)

本文研究的護理機器人為移動式仿人雙臂機器人,實體樣機如圖1 所示,由4 個全向輪、底盤框架、腰部、雙臂和手掌部分組成,具有輪式機器人和雙足機器人的優(yōu)點。 采用全向輪的底盤,靈活便于控制,穩(wěn)定性良好,與軀干機械臂組合成復(fù)合式機器人系統(tǒng),既增加了護理機器人的靈活使用性,又拓展了其工作范圍。 護理機器人共有15 個自由度,為高階非線性耦合系統(tǒng),底盤具有3 個自由度可實現(xiàn)整體縱、橫和回轉(zhuǎn)運動,腰部1 個俯仰自由度和1 個側(cè)傾自由度,每條手臂有5 個自由度。

圖1 護理機器人樣機Fig.1 Nursing robot prototype

1.2 連桿坐標(biāo)系的建立

首先,為每個桿件建立相對的參考坐標(biāo)系,確定從一個坐標(biāo)到下一個坐標(biāo)的變換步驟。 然后,從基座的第一個桿件依次變換結(jié)合起來,得到機器人的總變換矩陣,建立最終的運動方程,從而求解機器人的位姿。

根據(jù)D-H 連桿坐標(biāo)系建立機器人運動學(xué)模型,固連在連桿i上的固連坐標(biāo)系稱為{i},關(guān)節(jié)軸i-1 和關(guān)節(jié)軸i之間公垂線的長度為ai-1即連桿長度;夾角為αi-1;公垂線ai-1與關(guān)節(jié)軸i的交點到公垂線ai與關(guān)節(jié)軸i的交點的有向距離為連桿偏距di,ai-1的延長線和ai之間繞關(guān)節(jié)軸i旋轉(zhuǎn)所形成的夾角為關(guān)節(jié)角θi。 圖2 為護理機器人各連桿的連桿坐標(biāo)系,腰部關(guān)節(jié)的自由度分別為俯仰關(guān)節(jié)轉(zhuǎn)角θ1和側(cè)傾關(guān)節(jié)轉(zhuǎn)角θ2,左臂各關(guān)節(jié)的轉(zhuǎn)角分別為θl3、θl4、θl5、θl6和θl7,右臂各關(guān)節(jié)的轉(zhuǎn)角分別為θr3、θr4、θr5、θr6和θr7。

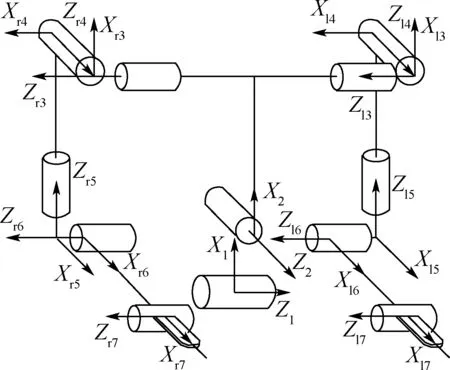
圖2 護理機器人各連桿的連桿坐標(biāo)系Fig.2 Linkage coordinate system of each linkage of nursing robot

考慮護理機器人初始狀態(tài)各肢體的相對位置,基于D-H 模型,可以得到護理機器人運動學(xué)的連桿參數(shù),如表1 所示。

表1 護理機器人運動學(xué)連桿參數(shù)Table 1 Nursing robot kinematic linkage parameters

根據(jù)連桿坐標(biāo)系模型的連桿參數(shù)計算出連桿的變換矩陣,從基座到末端把相應(yīng)的連桿變換矩陣依次相乘得到坐標(biāo)系{N}相對于坐標(biāo)系{0}的變換矩陣:

2 個桿件的坐標(biāo)系在世界坐標(biāo)系中相互變化時,在坐標(biāo)系沒有相對運動的情況下,通過2 次平移和1 次旋轉(zhuǎn)后2 個坐標(biāo)系可以重合。 建立各桿件相對應(yīng)的齊次坐標(biāo)變換矩陣,并將其定義為T矩陣。

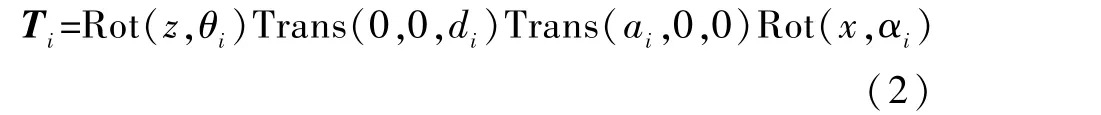
其變換矩陣為

建立護理機器人各桿件相對應(yīng)的齊次坐標(biāo)變換矩陣,得到護理機器人的正運動學(xué)方程為

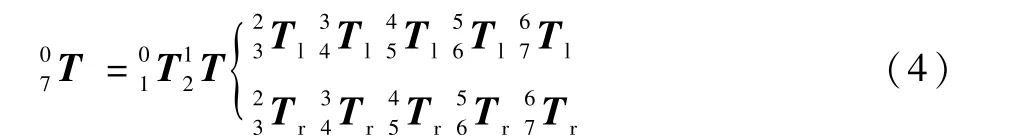
通過對雙臂結(jié)構(gòu)的分析可以將主體結(jié)構(gòu)分解為具有對稱結(jié)構(gòu)的獨立單臂在前2 個關(guān)節(jié)處重合形成的耦合結(jié)構(gòu)。 分解后的左右機械臂末端的手腕坐標(biāo)系在世界坐標(biāo)系中的位置和姿態(tài)為

1.3 正運動學(xué)的仿真

護理機器人的運動學(xué)模型通過MATLAB 中的機器人工具箱得到運動過程的位姿圖,輸出的位姿矩陣可以用來驗證所建立的機器人運動學(xué)模型的有效性和正確性。

將機器人初始狀態(tài)的各關(guān)節(jié)轉(zhuǎn)角值代入式(5)和式(6)中,利用MATLAB 的矩陣計算分別計算出機械臂的末端手腕關(guān)節(jié)的位姿矩陣為

將模型參數(shù)代入Roboticstoolbox 工具箱,通過工具箱的程序得到最終的位姿。 在MATLAB中對設(shè)計的機器人進行連桿模型簡化,對正運動學(xué)求解過程進行編程,仿真結(jié)果如圖3 所示。

圖3 機器人在MATLAB 中的模型Fig.3 Robot model in MATLAB

利用函數(shù)fkine 得到的正運動學(xué)的解與運動學(xué)方程得到的初始狀態(tài)末端手腕關(guān)節(jié)的位姿一致,證明本文所列運動學(xué)方程是正確的。

2 標(biāo)準(zhǔn)遺傳算法的逆運動學(xué)解

遺傳算法求機器人逆運動學(xué)問題的首要任務(wù)是確定遺傳算法的目標(biāo)函數(shù),以分解的左臂為對象,若P點是機械臂末端腕關(guān)節(jié)可達空間的一點,則點P對應(yīng)的當(dāng)前位姿矩陣Tp為

機器臂末端關(guān)節(jié)在直角坐標(biāo)系中的目標(biāo)位姿矩陣Te為

機械臂通常根據(jù)機器人末端目標(biāo)位姿和當(dāng)前位姿的差值作為整體優(yōu)化條件來計算適應(yīng)度的大小。 式(9)和式(10)為齊次變換矩陣,左上角3 ×3矩陣是機械手臂末端的姿態(tài)矩陣,此矩陣是一個單位矩陣,右上角3 ×1 列向量為機械手臂末端腕關(guān)節(jié)的坐標(biāo)系原點位置向量。 根據(jù)機器人位姿矩陣的表示方法,目標(biāo)位姿矩陣和當(dāng)前位姿矩陣的差值可寫成

式中:ΔP為位置向量差值;ΔO為姿態(tài)矩陣差值;關(guān)節(jié)變量θ(θ1,θ2,…,θ7)為遺傳算法的種群個體,則目標(biāo)函數(shù)為

式中:p和s分別為目標(biāo)位姿矩陣和當(dāng)前位姿矩陣的位置列向量;r和c分別為目標(biāo)位姿矩陣和當(dāng)前位姿矩陣的姿態(tài)矩陣;ω為條件系數(shù),當(dāng)末端無方向要求時,ω=0,當(dāng)末端有方向要求時,ω=1,由于護理機器人工作時需要調(diào)整末端姿態(tài),取ω=1。 對于護理機器人逆運動學(xué)的遺傳算法,適應(yīng)度函數(shù)為

利用標(biāo)準(zhǔn)遺傳算法進行最小值優(yōu)化,設(shè)置遺傳算法參數(shù)后在計算機中進行仿真實驗。

經(jīng)過50 次迭代后,種群中個體的目標(biāo)函數(shù)值分布如圖4 所示。 可以看出,初始種群個體的目標(biāo)函數(shù)值分布比較集中,容易產(chǎn)生局部最優(yōu)。

圖4 種群中個體的目標(biāo)函數(shù)值分布Fig.4 Distribution of objective function values of individuals in population

種群適應(yīng)度函數(shù)均值和最優(yōu)解隨遺傳代數(shù)的變化如圖5 所示。 可以看出,遺傳算法的適應(yīng)度函數(shù)和有效逆解基本收斂,但最終收斂值不是理想的0,而是從第10 次迭代后就過早停止了向全局最優(yōu)解進化,停滯在0.532 2 左右。

圖5 種群適應(yīng)度函數(shù)均值和最優(yōu)解的變化Fig.5 Variation of the mean value of population fitness function and optimal solution

關(guān)節(jié)空間遺傳算法優(yōu)化解位姿如圖6 所示。可以看出,標(biāo)準(zhǔn)遺傳算法所得到的最優(yōu)逆解和目標(biāo)位姿存在誤差,誤差對應(yīng)到有效逆解結(jié)果的位姿圖示上可以看出,機器人手臂末端點沒有達到目標(biāo)位姿的目標(biāo)點。

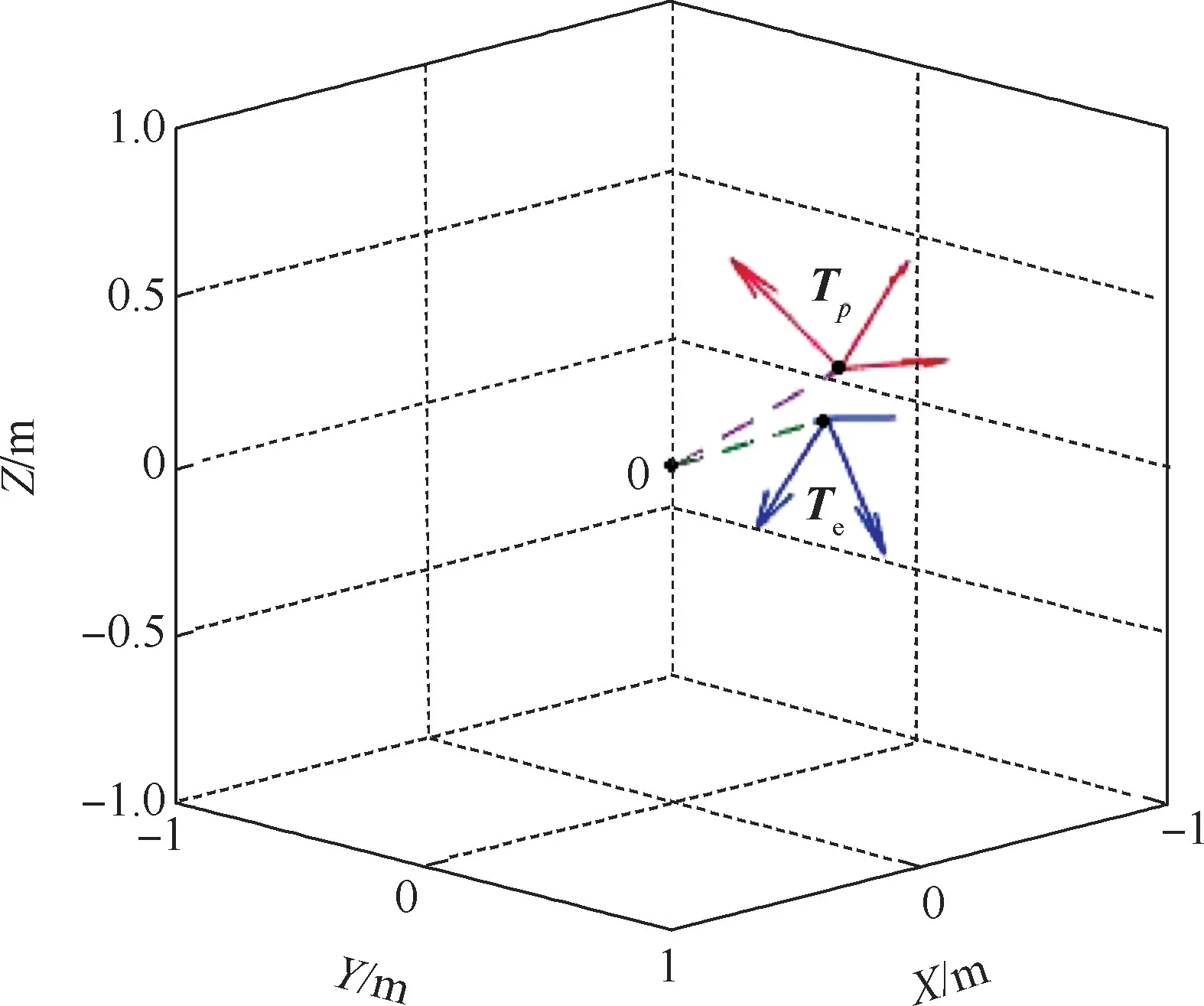
圖6 關(guān)節(jié)空間遺傳算法優(yōu)化解位姿Fig.6 Genetic algorithm optimization of pose in joint space

護理機器人手臂關(guān)節(jié)較多,設(shè)定的基本種群規(guī)模相對較小,而且適應(yīng)度函數(shù)值較大使得有效逆解不易被選取。 此外,適應(yīng)度函數(shù)以位姿偏差為核心,機器人運動到不同狀態(tài)時所處位置的位置偏差和姿態(tài)偏差變化方向不一致,個體很容易被淘汰,因此需要進一步優(yōu)化。

3 標(biāo)準(zhǔn)遺傳算法的改進算法

針對標(biāo)準(zhǔn)遺傳算法的不足,從增加群體多樣性和適應(yīng)度函數(shù)標(biāo)定2 個方面對標(biāo)準(zhǔn)遺傳學(xué)算法進行適當(dāng)改進,解決原始算法收斂速度慢和收斂精度低等問題,提高護理機器人逆運動學(xué)解的精度。

3.1 初始種群的產(chǎn)生

護理機器人關(guān)節(jié)轉(zhuǎn)角范圍相差大,且極其不均勻。 因此,在增加種群的基礎(chǔ)上采用等分區(qū)間的方法來產(chǎn)生初始種群,即將各個關(guān)節(jié)的轉(zhuǎn)角范圍等分成相等的5 個小區(qū)間,再在每個小區(qū)間隨機生成20 個個體,最后5 個小區(qū)間的所有個體一起來組成初始種群。

每個關(guān)節(jié)的運動范圍的表達式為

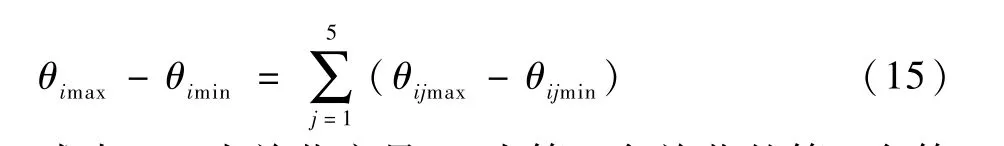
式中:θi為關(guān)節(jié)變量;θij為第i個關(guān)節(jié)的第j個等分區(qū)間。

關(guān)節(jié)運動范圍等分區(qū)間如圖7 所示,θ3的轉(zhuǎn)角范圍為π/4,θ5的轉(zhuǎn)角范圍為π。

圖7 關(guān)節(jié)運動范圍等分區(qū)間Fig.7 Joint range of motion equipartition interval

以θ3和θ5采用等分區(qū)間的方法前后產(chǎn)生初始種群的個體分布,如圖8 所示。 可以看出,采用等分區(qū)間的方法所產(chǎn)生的個體分散程度比整體隨機種群個體的分散程度高。

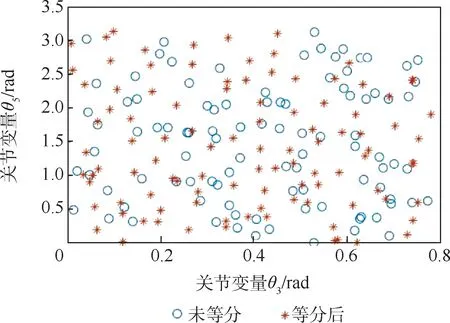
圖8 等分區(qū)間前后個體的分布Fig.8 Distribution of individuals before and after equipartition interval

因此,采用等分區(qū)間后不僅增大初始種群包含最優(yōu)解組合概率,而且避免了個體的不均勻分布,提高了搜索效率。

以等分區(qū)間方法產(chǎn)生的初始種群進行遺傳算法求解最優(yōu)解,其他參數(shù)設(shè)置基于標(biāo)準(zhǔn)遺傳算法,運行算法得到適應(yīng)度函數(shù)均值和最小值隨代數(shù)的變化,如圖9 所示。 可以看出,最優(yōu)解在30 代是基本收斂到最小值,雖然沒有得到較小的解,但延長了進化代數(shù),推遲了早熟進程,提高了算法的可靠性。

圖9 等分區(qū)間種群適應(yīng)度函數(shù)均值和最優(yōu)解的變化Fig.9 Variation of the mean value of population fitness function and optimal solution in equipartition interval

3.2 適應(yīng)度函數(shù)的選擇

隨機產(chǎn)生的種群適應(yīng)度值較大的個體統(tǒng)治著整個初始種群,進化到最優(yōu)個體之前停止進化,以至于無法產(chǎn)生全局最優(yōu)解。 進化過程中個體適應(yīng)度的值基本不變,造成了獲得的最優(yōu)解不是全局最優(yōu)解。 為了解決該問題,通過反復(fù)地對比與運算,在適應(yīng)度函數(shù)中加入了可變權(quán)因子β,隨迭代次數(shù)基于位姿誤差的最小可變權(quán)因子,改進后適應(yīng)度函數(shù)的計算式如下:

在進化開始時位置誤差和姿態(tài)誤差應(yīng)分配相同的權(quán)重,初期位置誤差較大,而姿態(tài)誤差變化一直較小,因此可變權(quán)因子β表達式為式(17)。 在迭代進化過程中,β隨著ΔP的改變而改變,ΔP的值在算法開始時一般比較大,此時β值接近于0.5;隨著進化過程的繼續(xù)進行,到了一定的代數(shù)以后,ΔP值逐漸變小,而β接近于1。 加入可變權(quán)因子β后的適應(yīng)度函數(shù),可以為位置誤差和姿態(tài)誤差在進化過程中分配合適的權(quán)重,確保了進化過程向全局最優(yōu)解的方向進行收斂。

3.3 改進算法的仿真分析

在標(biāo)準(zhǔn)遺傳算法運動學(xué)逆解程序的基礎(chǔ)上,按等分區(qū)間劃分產(chǎn)生種群,并且使用加入變權(quán)因子的適應(yīng)度函數(shù),進行仿真分析。 經(jīng)過50 次迭代后,種群中個體的目標(biāo)函數(shù)數(shù)值分布如圖10 所示。 可以看出,個體的目標(biāo)函數(shù)值分散程度高,保證了種群的多樣性。

圖10 改進算法種群中個體的目標(biāo)函數(shù)值分布Fig.10 Distribution of objective function values of individuals in population of improved algorithm

種群適應(yīng)度函數(shù)均值和最優(yōu)解隨遺傳代數(shù)的變化如圖11 所示。 通過算法改進前后的變化對比可以看出(見圖5 和圖11),在經(jīng)過10 次迭代后,改進算法開始快速收斂于全局最優(yōu)解,且適應(yīng)度函數(shù)均值和最優(yōu)解的函數(shù)值趨近于0,收斂精度高,可以得到精確的最優(yōu)解。

圖11 適應(yīng)度函數(shù)均值和最優(yōu)解隨遺傳代數(shù)的變化Fig.11 Variation of the mean value of fitness function and optimal solution with number of genetic generations

關(guān)節(jié)空間遺傳算法優(yōu)化解位姿如圖12 所示。對比圖6 可以看出,目標(biāo)位姿和當(dāng)前位姿基本重合,誤差很小。

圖12 關(guān)節(jié)空間改進算法優(yōu)化解位姿Fig.12 Optimization of pose in joint space using improved algorithm

改進遺傳算法可以有效解決機器人運動學(xué)逆解,為護理機器人手臂的運動學(xué)逆解算法提供了一種新的思路,也可為實現(xiàn)機器人智能運動規(guī)劃提供參考。

4 實驗驗證

在實驗室環(huán)境中,搭建三坐標(biāo)測量系統(tǒng)對護理機器人末端姿態(tài)進行測試。 通過攝影測量實現(xiàn)姿態(tài)的精準(zhǔn)測量。 圖13 為測試系統(tǒng)實物圖,包含數(shù)碼相機、測量光筆、工控機及軟件系統(tǒng)。

圖13 三坐標(biāo)測量系統(tǒng)Fig.13 Three coordinate measuring system

通過測量光筆的位姿來間接測量護理機器人手臂的末端姿態(tài)位置,光筆的測量精度決定了測量準(zhǔn)確性。 采用CLP 6800 的光筆,其測量精度為±0. 03 mm,工作溫度0 ～45℃,可以滿足系統(tǒng)需求。 圖14 為測試實驗圖,操作人員手持光筆,在數(shù)碼相機的有效拍攝范圍內(nèi),對目標(biāo)點進行測量,光筆外側(cè)的LED 要指向數(shù)碼相機。

圖14 測量實驗Fig.14 Measurement tests

以護理機器人水平抱舉姿態(tài)為目標(biāo)位姿點,對應(yīng)的左臂末端位姿矩陣為

基于改進遺傳算法求得的最優(yōu)解InvsolL 為[0.444 6 -0.087 7 0.674 2 1.573 3 1.860 3-0.305 1 -0.162 9]。 護理機器人根據(jù)運動學(xué)逆解到目標(biāo)位置后,對目標(biāo)點進行測量。 測量得到的左臂末端的位姿為

對比分析其位姿誤差ΔE,其中位置誤差ΔP為末端執(zhí)行器坐標(biāo)系原點的位置向量與目標(biāo)點位置向量差的模的平方:

姿態(tài)誤差ΔA為護理機器人末端執(zhí)行器坐標(biāo)系各個坐標(biāo)軸向量與對應(yīng)目標(biāo)點坐標(biāo)軸向量差的模減1 的平方:

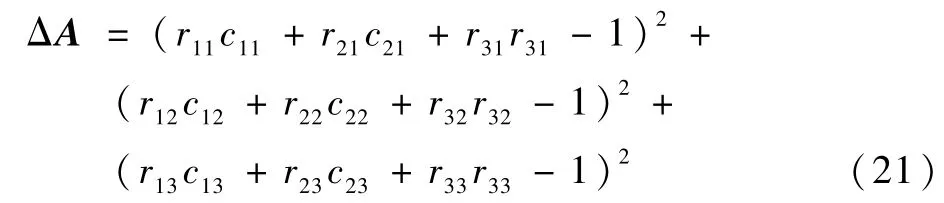
計算可得到左臂末端位置的位姿誤差ΔEl為0.886 ×10-3m。 實驗中右臂和左臂的運動一致,因此主要對左臂進行分析和實驗。

從計算結(jié)果可以看出理論目標(biāo)位置和測量目標(biāo)位置之間存在一定的誤差,但對于主要抱取病人的護理機器人來說,誤差在允許的范圍內(nèi)。

5 結(jié) 論

1) 本文采用等分區(qū)間法產(chǎn)生的初始群體不僅增大了包含最優(yōu)解組合的概率,而且避免了個體的不均勻分布,提高了搜索效率。

2) 在適應(yīng)度函數(shù)中加入基于位姿誤差的最小可變權(quán)因子,確保了進化過程向全局最優(yōu)解的方向進行收斂。

3) 通過搭建實驗測試系統(tǒng),結(jié)果表明改進后的遺傳算法求得的逆向運動學(xué)解為最優(yōu)全局解,護理機器人的位姿誤差較小。