函數型正則廣義典型相關分析

王志超 TENENHAUS Arthur 王惠文 趙青

(1. 中國工商銀行 博士后科研工作站, 北京 100032; 2. 法國高等電力學院 信號處理與電子系統系, 吉夫伊維特 91192;3. 北京航空航天大學 經濟管理學院, 北京 100083;4. 北京航空航天大學 復雜系統分析與管理決策教育部重點實驗室, 北京 100083)

Abstract: An effective dimension reduction method for multivariate functional data is developed within the theoretical framework of regularized generalized canonical correlation analysis. Functional data in square integrable spaces is first projected in an integral form to a series of numeric variables, and those variables are then used for simultaneously determining the related projection directions of functional features by maximizing a kind of global correlation measure, which achieves the featured information extraction and rapid dimension reduction of multivariate functional data as traditional numeric variables. A general basis function system is used to create the iterative computing algorithm for the optimal functional projection weights, which is independent of the specified basis functions. A large number of simulation results for infinite samples show that the proposed method is able to detect the correlation among multivariate functional data and obtain consistent estimates for the associated functional projection weights. The real-data study on the gait of Parkinson’s patients indicates the interpretability of the numeric featured information derived from the original functional data and the utility of the proposed method.

Keywords: functional data; regularized generalized canonical correlation analysis; feature extraction;functional principal component; gait of Parkinson’s syndrome

隨著傳感器、硬件存儲等信息技術的快速發展,數據信息的獲取得到極大便捷,可供使用的數據資料不再局限于傳統單點型數值變量,而具有復雜多樣的表現形式和內在特征。 作為新興復雜數據類型之一,函數型數據描述一類指標變量隨時間、空間等因素連續變化的曲線[1],被廣泛應用于眾多研究領域[2-7]。 例如,對于壓力傳感器實時監測的記錄,以及高頻變動的股票日內價格和收益率,這些指標應當認為是連續變化的,而不僅僅是若干時間點觀測的離散數值。 曲線的無窮維特征,成為函數型數據分析(functional data analysis, FDA)需要解決的關鍵問題;因此,許多對于函數的等價表達方法被陸續提出,如基函數展開和重生核表示等[8]。

在日趨復雜的應用場景中,往往需要同時考慮2 個甚至更多函數型變量之間,或函數型變量與數值變量之間的關系。 面對數據多樣化引發的高維問題,需要對多元函數型數據進行降維處理;對此,一種有效的解決方法是:從函數型數據中提取一系列蘊含原函數特征信息的數值變量用于后續統計建模。 按照這一思路,Ferre 和Yao[9]提出基于切片逆回歸(sliced inverse regression, SIR)的函數型數據充分降維方法;Wang 等[10]進一步提出函數型SIR 方法的穩健估計;Reiss 和Ogden[11]則通過函數型主成分回歸和函數型偏最小二乘(partial least squares, PLS)方法確定函數型數據的展開表示。

現有研究主要根據函數型數據變量內部變化信息或模型設定實現特征信息的數值化表達,當變量個數較多時,逐一進行特征信息提取不僅效率低下,且無法建立不同函數曲線之間的聯系。基于SIR 和PLS 的方法雖然考慮了兩兩函數型變量之間的相關關系,但很難適用于更多變量的情形。 Tenenhaus 父子[12-14]提出的正則廣義典型相關分析(regularized generalized canonical correlation analysis, RGCCA)將眾多分塊數據分析方法進行推廣統一,得到許多推廣和應用[15-18]。

為了實現多元函數型數據的特征信息提取及快速降維過程,本文在FDA 框架下,考慮函數型RGCCA(functional RGCCA, FRGCCA)。 具體來說,FRGCCA 沿一系列函數型積分投影方向將多元函數型數據投影至若干組數值變量;在整體相關性度量最大的準則下,借助函數型主成分分析(functional principal component analysis, FPCA)方法,確定主成分基函數展開系數,并最終估計最優積分投影方向。 經過大量數值驗證,本文方法被驗證能夠快速有效探測多元函數型數據之間的相關關系,并得到相應最優投影權重函數的一致估計。 在實例研究中,通過帕金森綜合征患者步態數據表明,由多元函數型數據投影得到的數值特征信息具有可解釋性,本文方法具有一定實用價值。

1 FRGCCA 優化模型

考慮函數型隨機變量{X(t):t∈F},F表示連續指標集。 對于任意t∈F,設X(t)均為數值隨機變量,并存在二階矩,即E[X2(t)] ＜∞,簡記為X∈L2(F)。 這樣,函數型數據的平方積分內積可以表示為

如式(1)所示,函數型數據X沿投影權重函數α被變換至一個數值積分投影。

對于J個函數型隨機變量Xj∈L2(Fj)及其對應投影權重函數αj(j=1,2,…,J),FRGCCA 考慮極大化整體的相關性度量,即

式中:連接參數cjk表示第j和第k個函數型隨機變量之間是否存在關聯性,當認為Xj與Xk相關時,cjk=1,否則為0;非負凸函數g(·)為給定的相關性度量;Cov(·,·)表示數值隨機變量或隨機向量之間的協方差或協方差矩陣。

與此同時,待估參數αj需要滿足一定約束條件,即

式中:Var(·)為數值隨機變量的方差;收縮參數τj∈[0,1]平衡投影方向長度和投影方差兩方面約束,特別當τj=1 時,FRGCCA 具有多元PLS 的形式,當τj=0 時,FRGCCA 退化為廣義典型相關分析。

2 FRGCCA 參數估計

本文重點討論FRGCCA 的參數求解過程,即在式(4)約束條件下,使整體相關性度量式(3)達到最大的一系列最優投影權重函數的估計方法。

2.1 基函數展開

給定Fj上一組基函數?j= (?j1,?j2,…,?j,Sj)T,Sj為維數,對于任意t∈Fj,Xj可以表示為

2.2 最優投影權重函數估計

通過上述基函數展開表達,式(3)可以表示為

式中:Σjk= Cov(Uj,Uk);λj為拉格朗日乘子。

由L(aj,λj;j=1,2,…,J)關于aj的偏梯度可以得到平穩方程:

式(12)的推導過程詳見附錄A。

式(13)和式(14)優化過程基于一系列給定的基函數系統,即?j(j=1,2,…,J)。 事實上,?j的選取不會影響Fj上最優投影權重函數αj的最終結果(過程詳見附錄B)。

本文所提出FRGCCA 的求解算法總結如下:

步驟1 初始化。

如果ω≤ωmax,或者

注:本文采用基函數展開方法將函數型數據轉換為一系列數值展開系數,通過對多組展開系數進行分析建模,以此重構得到對應函數型投影權重的相關結果。 這一建模思路表明:本文所提出的FRGCCA 方法同樣適用于多組數值數據與一個或多個函數型數據同時存在的混合數據情形。 此時,數值變量和函數型變量分別在實向量空間和平方可積空間中通過各自投影實現數值化降維。 具體來說,在式(11)中,不妨假設第j個變量Xj退化為數值變量,此時選取實向量空間中的自然基?j,那么對應度量矩陣Wj退化為單位矩陣,aj即為Xj在?j下的投影權重向量。 相應計算過程與上述FRGCCA 求解算法保持一致。

2.3 其他因素

選取特定參數形式的基函數往往具有一定主觀性[19];對此,本文采用基于數據驅動的FPCA方法確定基函數系統。 具體來說,在給定?j的基礎上,FPCA 希望找到某個函數ξj∈L2(F),使得Xj與ξj的數值積分投影的方差最大:

令vj表示ξj在?j下的展開系數,則式(15)等價于求解關于vj的多元主成分問題:

式中:0≤l0≤1 為設定的累積方差貢獻率閾值。

通過標準正交基函數系統ξ0j= (ξ1j,ξ2j,…,

式中:mjkl(k,l=1,2,…,Sj)為Mj中第k行、第l列元素,mjkl和mjkk的方差用相應無偏估計替代。

3 數值實驗

本節從3 個方面檢驗所提出FRGCCA 方法在有限樣本情況下對多元函數型數據進行特征信息提取的表現,即函數型數據樣本量、特征信息強度及觀測擾動強度、收縮參數設置。

3.1 生成模型

考慮3 個定義在不同區間Ij上的函數型變量Xj(j=1,2,3),Xj由Ij上通過等間隔內節點決定的3 次B 樣條基函數?j= (?j1,?j2,…,?j,Sj)T線性生成,生成系數為Uj。

對于非對角分塊,

在3 組展開系數中,依次假設第2 至第3、第4 至第7、第8 至第11 個展開系數分量之間是相關的。 那么當τj=1 時,W1/2j aj的理論最優解為單位化向量(0,0,…,0,1,1,…,1,0,0,…,0)T,其中取值為1 的分量對應具有相關性的展開系數分量。 在上述假設下,首先從U中獨立生成Xj的n組展開系數uij(i=1,2,…,n),然后在Ij上等概率選取T個時刻tj,并生成一系列數值觀測:

式中:Φj(tj)為如式(6)所示的數據矩陣;εij(tj)為從標準正態分布中獨立產生的觀測擾動;σ＞0為控制擾動強度。

在每次實驗中,假設3 個函數型變量之間兩兩相關,并使用Horst 型單位函數作為相關性度量;在FPCA 確定基函數系統過程中,選取通過相應區間上17 個等間隔內節點決定的3 次B 樣條函數作為初始基函數。 記通過FRGCCA 估計得到的最優投影權重函數及其對應展開系數分別為^αj和^aj,用積分平方誤差(integral square error,ISE)衡量^αj的估計精度,即

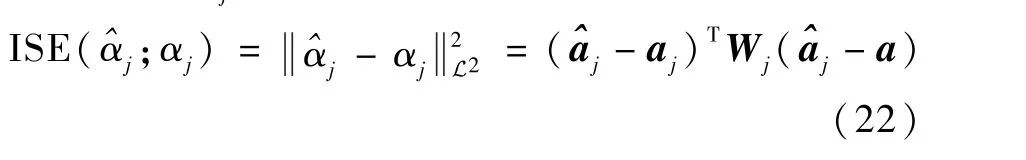
對于式(21)生成模型中的每種參數設置,獨立重復進行1 000 次數值實驗。

3.2 函數型數據樣本量

考慮不同函數型數據樣本量n對^αj的影響。在式(21)生成模型中,依次從n=200 增加至n=1 000,并固定T=200、σ=0.1 及收縮參數τj=1(j=1,2,3)。 表1 報告了不同函數型數據樣本量情況下,^αj關于αj理論最優解的ISE(放大100 倍)的均值和標準差。

從表1 中可以看到,隨著n的增加,^αj的均值與相應理論最優解的差距一致減小,其標準差也同步減小;基于FPCA 生成基函數得到的估計結果,逐步趨近于已知真實設定基函數系統及投影權重函數展開系數的理想情況。 上述數值結果表明,所提出FRGCCA 方法能夠在有限樣本情況下對αj的估計具有一致性。

表1 不同函數型數據樣本量下FRGCCA 的估計精度Table 1 Estimation accuracy of FRGCCA under different sample sizes of functional data

3.3 特征信息及擾動強度

用函數型數據中數值觀測量T的大小來衡量相應特征信息強度,考慮T對^αj的影響。 在式(21)生成模型中,依次設T=50,100,…,300,并固定n=500、σ=0.1 及τj=1(j=1,2,3)。 表2 報告了不同數值觀測量情況下,關于αj理論最優解的ISE(放大100 倍)的均值和標準差。

從表2 中可以看到,當函數型數據中數值觀測量較少(如T=50)時,對αj的估計也普遍較差;當觀測量適量增加時,相應估計結果將顯著提升,并同樣接近真實設定基函數系統及投影權重函數展開系數已知情況下的理想結果。 然而,在達到一定規模(如T=200)后,由于基函數展開存在截斷誤差,過多的數值觀測無法進一步提高估計精度。

表2 不同數值觀測量下FRGCCA 的估計精度Table 2 Estimation accuracy of FRGCCA under different sizes of observations

在本節參數設置基礎上,固定T=200,并考慮不同擾動強度σ∈{0,0.2,…,1}。 特別地,σ=0 表示生成模型中不存在觀測擾動,但由于使用FPCA 確定基函數系統,相應展開系數并不等同于由分布生成的真實設置。 表3 報告了不同數值觀測擾動強度情況下,^αj關于αj理論最優解的ISE(放大100 倍)的均值和標準差。 從表3 中可以看到,增加σ雖然從整體上增加了^αj的偏差,但增加程度相對較小。

由表1 ～表3 可知,在FPCA 確定基函數系統過程中,設定較小的累積方差貢獻率閾值(如l0=0.8)即可得到較好的估計結果;設定過大的累積方差貢獻率閾值(如l0=0.99)將引入不必要的觀測擾動信息,從而干擾優化過程,使得估計結果產生一定偏差和波動。 此外,累積方差貢獻率閾值的經驗設定可以根據函數型數據的數值觀測量進行調整。 當數值觀測不足時,需要通過較多的基函數展開系數盡可能挖掘函數型數據的變化特征,即設置較大的l0;而當觀數值觀測較多時,則需要適當減少使用的展開系數個數,以避免過擬合。 不過,累積方差貢獻率閾值的設定并不會對投影權重函數的估計產生顯著影響。

表3 不同數值觀測擾動強度下FRGCCA 的估計精度Table 3 Estimation accuracy of FRGCCA under different perturbations of observations

3.4 收縮參數

考慮不同收縮參數τj對^αj的影響。 在式(21)生成模型中,設n=600、T=200 且σ=0.1。 為了衡量^αj的整體波動,考慮^αj在Ij上的積分方差(integral variance, IVar),即

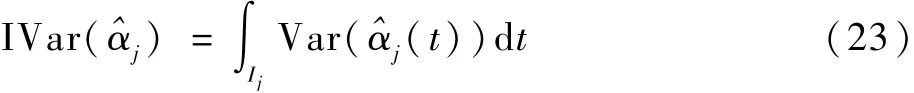
圖1 展示了收縮參數從1 同步變化至0 情況下,相應IVar(^αj)的折線圖。 圖中:豎直線段表示均值加減一個標準差范圍。 此外,設l0=0.9。

如圖1 所示,隨著τj減小,IVar(^αj)的均值和標準差顯著增加,這意味著^αj逐漸偏離τj=1 時αj的理論最優解,并具有更大波動。 事實上,在式(4)約束條件中,τj=1 要求αj具有單位函數長度,這使得αj無法變化很大;當τj逐漸減小時,這種約束隨之減小,αj的變化程度則相應增加。圖1驗證了τj在FRGCCA 中的正則化功能,這與傳統RGCCA 框架中的有關結論是一致的。

圖1 不同收縮參數下FRGCCA 估計結果的Ivar 折線圖Fig.1 Line chart for IVar of FRGCCA under different shrinkage parameters

4 實例分析

本節通過有關帕金森綜合征患者行走步態的實例數據(簡稱Gait 數據集)檢驗所提出FRGCCA 方法的實用性。 表4 簡要介紹了本文使用的Gait 數據集中4 組指標變量,更加詳細的描述參見Goldberger 等[21]的研究。

表4 Gait 數據集指標變量說明Table 4 Gait dataset indicator variables description

值得說明的是,在Gait 數據集中,同時存在若干組數值變量(患者體型等)和一個函數型變量(實時步態)。 按照本文所提出FRGCCA 方法采用的基函數展開思路,函數型數據和傳統數值數據混合的情形同樣適用于本文方法。 本文只需將函數型變量轉化為對應的基函數展開系數。

首先將高頻采集的TFULF 原始數據曲線進行分割,通過核函數估計方法對一系列分割的原始曲線進行擬合,并對齊至0 ～1 的區間,其中0和1 分別表示一步行走的開始和結束。 圖2 展示了編號為“GaPt28”和“SiPt08”患者的TFULF 原始數據和擬合曲線。

圖2 Gait 數據集TFULF 曲線示意圖Fig.2 Diagrams of curves of TFULF for Gait dataset

然后對上述指標變量建立FRGCCA 模型。采用Horst 型單位函數作為相關性度量,令收縮參數均為1,并假設“患者體型”與“患病程度”2組指標變量之間不存在相關性,那么相應關聯關系矩陣為

在FPCA 確定基函數系統過程中,將通過[0,1]中17 個等間隔內節點決定的3 次B 樣條函數作為初始基函數,并設l0=0.95。 與此同時,通過重抽樣算法構造投影權重函數估計的置信域,并進行1 000 次獨立重復實驗。 在每次重復實驗中,有放回選取80%實驗數據。 表5 報告了通過全樣本估計得到的3 組多元數值變量的最優投影方向估計及其相應經驗置信區間。 圖3 展示了函數型變量TFULF 對應最優投影權重函數的全樣本估計及5%置信水平下的經驗置信帶。

表5 三組多元數值變量對應投影權重向量的估計結果Table 5 Estimated results of corresponding weighted integral vectors for three multivariate groups

從表5 中可以看到,在“患病程度”分組中,投影權重向量的分量均為正數,這說明通過投影得到的數值特征信息與帕金森綜合征患者的患病程度呈正相關關系。 與此同時,“步態特征”分組對應投影權重向量也印證了這一事實,即患病越嚴重,患者行走速度越慢、完成一個步態周期所需的時間也就越長。 在此基礎上,“患者體型”分組對應估計結果說明,對于帕金森綜合征患者而言,身高越高或體重越大均會加重患病的嚴重程度,且體重對于患病程度的影響更大。 在經驗置信區間方面,FRGCCA 得到估計結果的置信區間普遍較窄,且在5%置信水平下均顯著不為零。

從圖3 中可以看到,TFULF 對應的最優投影權重函數估計曲線在步態周期開始(完成20%前)和結束(完成80%左右)存在2 個顯著高于零的波峰,這一結果說明起步和收尾階段的步態情況對判斷帕金森綜合征患者的患病程度存在顯著關聯。

5 結 論

本文提出對于多元函數型數據的RGCCA 理論,即FRGCCA,并推導其迭代求解算法。

1) 本文所提出FRGCCA 方法將RGCCA 的理論框架推廣至FDA 領域,實現了對多元函數型數據特征信息的數值化提取及快速降維。

2) 通過基函數展開方法,推導得到關于最優函數型投影權重方向的迭代估計方法,該方法對于基函數系統的選取具有獨立性。 通過基于數據驅動的FPCA 方法確定標準正交的基函數系統。

3) 通過一系列數值實驗,從3 個方面說明了所提出FRGCCA 方法在有限樣本情況下對投影權重函數的估計具有一致性,并有效實現多元函數型數據特征信息的數值化提取及快速降維。

4) 在對于Gait 數據集的實例數據研究中,所提出FRGCCA 方法得到的數值特征信息與患病程度呈正相關關系,由此驗證了所提出方法的實用價值。

附錄A：

附錄B：

此時由式(B2)可以驗證