基于PSO-BP 神經網絡的平流層風場短期快速預測

龍遠 鄧小龍 楊希祥 侯中喜

(國防科技大學 空天科學學院, 長沙 410073)

平流層是處于對流層與中間層之間、海拔高度為10 ～55 km 的大氣空間[1],平流層內氣流相對平穩、垂直對流小[2],是部署平流層飛艇、高空氣球、高空太陽能無人機等臨近空間低速飛行器執行對地觀測、監視預警、通信中繼、環境監測及科學研究等軍民任務的理想環境[3-6]。

由于飛行速度低、動力系統弱、控制能力有限等約束,臨近空間低速飛行器的飛行性能受其所處環境風場影響較大[7-8]。 例如,平流層飛艇的駐留能力直接取決于風場環境[9],而高空太陽能無人機的氣動特性及續航里程也受到風場環境重要影響。 因此,開展平流層風場研究,獲取準確的風場預測信息對于臨近空間低速飛行器開展飛行任務規劃、航跡規劃和飛行控制都具有重要意義[10]。

目前,可用于平流層風速預測的方法主要包括2 類:數值天氣預報方法和統計模型方法[11]。數值天氣預報需要建立復雜的物理模型和龐大的計算系統,通過氣象學理論和計算流體力學得到風速、風向、溫度、濕度等氣象要素的預測值。 而統計模型方法主要采用數學統計的思想,通過挖掘數據間存在的內在規律進行預測,此類方法包括時間序列法、卡爾曼濾波、神經網絡等。 常規數值天氣預報系統主要關注對流層內與人類社會經濟活動密切相關的氣象信息,平流層的風場預測沒有得到足夠的重視,精度還有待提高[12],且對飛行器研制與應用部門的環境保障要求高。 因此,在平流層風場預測中,通常采用統計模型的方法。

國內外學者對統計模型方法在風場預測中的應用展開了大量研究。 文獻[13]通過本征正交分解(POD)方法建立了風場降階模型,再利用傅里葉級數擬合對平流層風場進行預測;文獻[14]利用POD 方法對具有橋塔風效應的風場進行了簡化模擬,將POD 型譜表示法取代原型譜表示法,物理意義明確且可通過模態截斷節省計算量;文獻[15]根據歷史風場統計數據建立了韋伯分布模型,利用韋伯分布和累積函數對歷史數據進行預測和反算,驗證了將韋伯分布應用于風場數據統計的合理性;文獻[16]提出了一種基于高斯過程(Gaussian processes,GP)的風速預測模型,將其與支持向量機、最小二乘支持向量機和BP 神經網絡進行比較,仿真結果表明,基于GP 的風速預測模型具有很好的穩定性,能夠滿足預測精度的要求;文獻[17]建立了高斯過程回歸和粒子濾波相結合的短期風速預測模型,實現了對歷史風速序列異常值的在線動態檢測與修正;文獻[18]利用平流層風場緯向風存在一定周期性和規律性的特點,分別采用傅里葉級數擬合方法和BP 神經網絡算法對風場快速預測進行了研究,并對2種方法的預測誤差與預測精度進行了分析;文獻[19]研究了數據增強和自校正設計在平流層風場建模中的應用,將美國國家海洋與大氣管理局提供的風場預報數據和高空氣球實測風場數據相結合,構建了可用于高空氣球軌跡規劃的風場預測模型。

上述研究大多專注于對流層內的風場預測問題,在平流層風場預測方面的研究較少,且較多集中于短期單點預測,無法滿足臨近空間低速飛行器進行路徑規劃所需的區域風場環境。 在已有研究的基礎上,本文根據歷史風場數據,先采用主成分分析(principal component analysis, PCA)法對數據進行降維處理,再通過訓練BP 神經網絡對風場進行預測,并利用粒子群優化(partical swarm optimization, PSO)算法對BP 神經網絡進行優化。 針對臨近空間低速飛行器飛行區域廣、單點預測風場數據無法滿足長時間飛行需求,進一步研究Biharmonic 樣條曲面插值方法對多點風場預測結果進行空間插值,構建了平流層區域預測風場,能夠為長航時臨近空間低速飛行器提供數據支撐。

1 平流層風場數據降維方法

基于統計模型的風場建模方法需要從海量歷史環境數據開始分析,這類數據的數據量大、特征不清晰,有必要預先進行降維處理,在保證原有信息損失不大的前提下,盡可能降低數據量的大小。PCA 則是最常用的一種降維方法。 PCA 能夠找出數據里面最主要的方面,用數據里最主要的方面來代替原始數據。

假設有某一坐標點記錄的n×m維歷史風場數據集X,數據集共有m個風場數據(x1,x2,…,xm),每個風場數據都是n維列向量,代表著坐標點某一時刻的風速在不同采樣高度處的取值,n為采樣點總個數。 為了降低風場數據量的大小,需要對其進行降維處理,在降維的過程中,要獲得原始數據新的表示空間,需要對原始數據進行線性變換(基變換),矩陣表示如下:

式中:Y為風場數據樣本在新空間的表示;P為r×n維變換矩陣;X為原始風場數據樣本;pi表示第i個基;xj表示第j個原始風場數據。

選擇不同的基可以對一組數據給出不同的表示,同時,當基的數量少于原始樣本本身的維數時,則可以達到降維的效果,PCA 就是要找到能夠最大限度保留原有數據信息的一組基P,具體分析步驟如下:

步驟1 樣本中心化處理。 為了簡便運算,需要對風場數據樣本進行中心化處理,得到新的數據樣本:

步驟3 求特征值及特征向量。 求解得到新風場數據樣本協方差矩陣的特征值λ1,λ2,…,λn,以及對應的單位特征向量?1,?2,…,?n。

步驟4 確定降維維度r。 將第r個主成分保留的信息稱作相對模態能量,表示為

根據風場數據的信息保留量(即累積模態能量的大小)來確定選取的主成分個數r,該數值即是降維后的數據維度,r＜n。

步驟5 求新變換矩陣P。 按風場數據樣本協方差矩陣特征值的大小將前r個特征值對應的特征向量從上向下按行排列成矩陣,該矩陣就是要求的變換矩陣P。

Y=PX即為降維到r維后的風場數據。

2 基于神經網絡的平流層風場預測方法

在對風場數據進行降維處理后,數據量大大減小,可用神經網絡學習風場的變化特征以對未來短期風場進行快速預測。 本節研究基于BP 神經網絡的風場預測方法,并通過具備全局尋優特性的PSO 算法來改進容易陷入局部最優的BP 神經網絡。

2.1 BP 神經網絡風場預測模型

本節建立的風場預測模型使用的神經網絡包含輸入層、隱含層和輸出層3 層,其中輸入層的神經元個數根據降維后的風場數據維數設置為3,輸出層神經元個數設置為1,隱含層神經元個數根據經驗公式設置為12,經驗公式如下:

式中:q為隱含層神經元個數;k和l分別為輸入層和輸出層神經元個數;a為常數,a∈[1,10]。

如圖1 所示,BP 神經網絡每個神經元都與上一層的所有神經元相連,隱含層和輸出層每個神經元的輸出與輸入之間的關系如下:

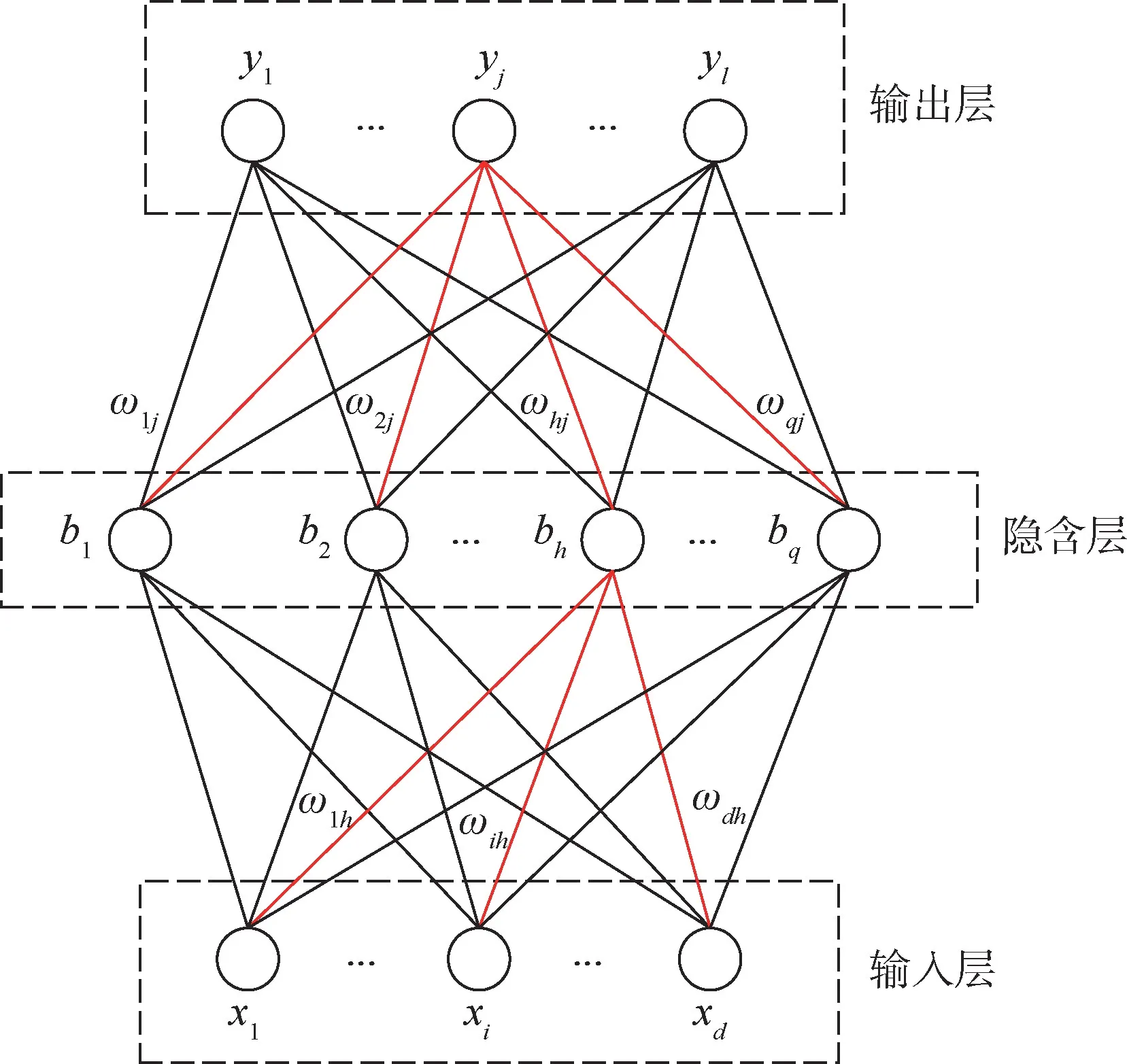
圖1 神經網絡結構Fig.1 Structure of neural network

式中:xi為神經元的輸入信號,即風場數據;ωi為輸入信號的權值;θ為神經元的閾值;f(·)為激活函數。

本節使用的激活函數為Sigmoid 函數:

假設在進行降維處理后,有r×m維風場數據Y=(y1,y2,…,ym),將其分為r個行向量,利用神經網絡分別對這r個行向量的數據變化特征進行學習,神經網絡訓練集的輸入數據和輸出數據的構建如圖2 所示,將m個風場數據分成m-3組訓練數據,每組訓練數據包含3 個輸入和1 個輸出。

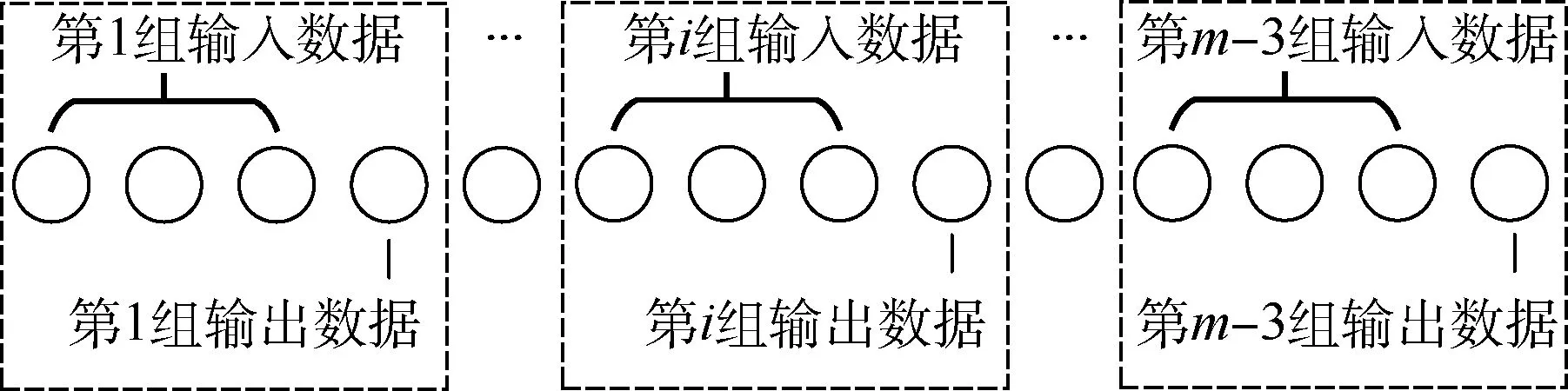
圖2 神經網絡的輸入和輸出Fig.2 Input and output of neural network

2.2 PSO-BP 神經網絡風場預測模型

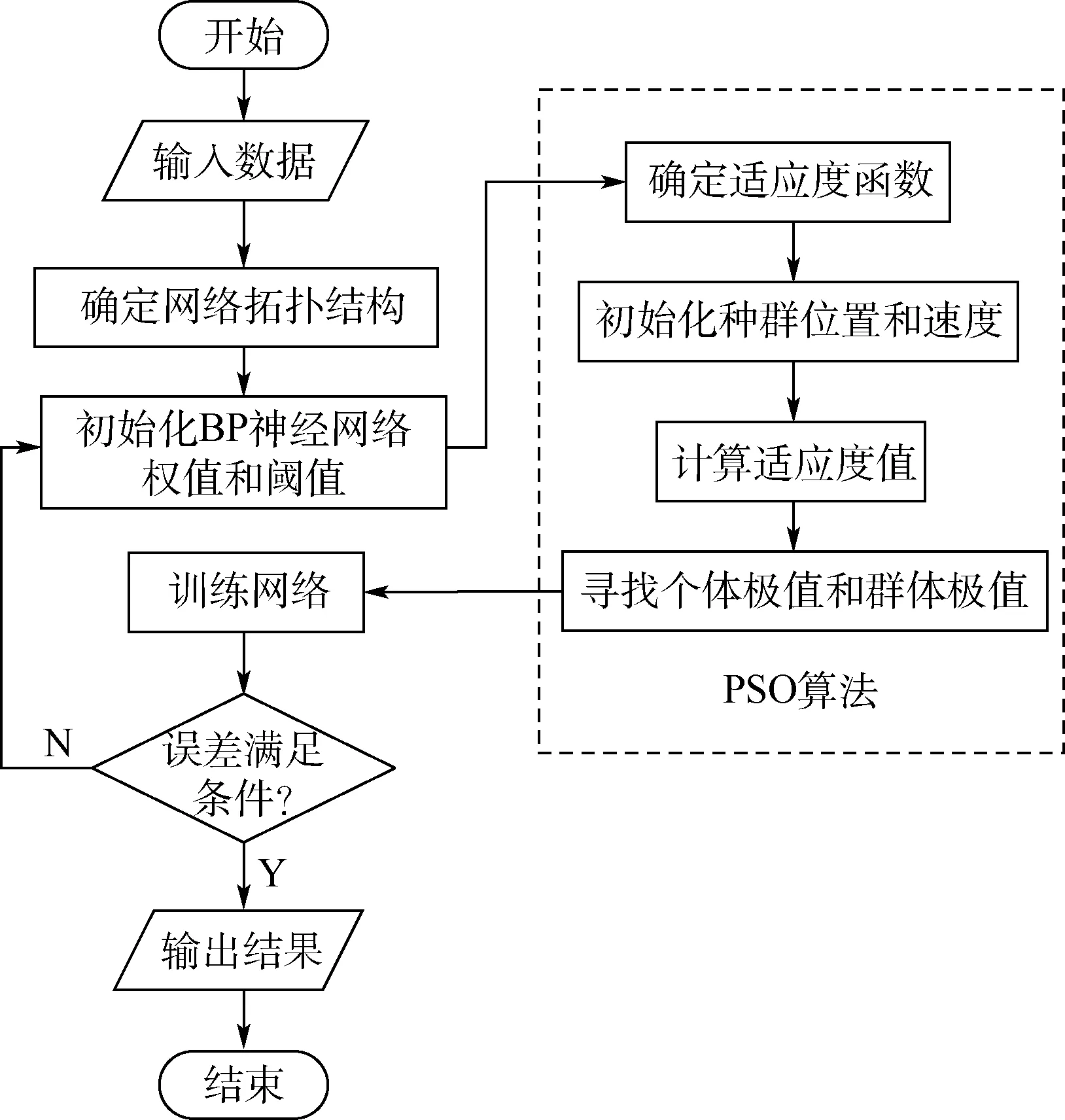
圖3 PSO 算法的BP 神經網絡原理Fig.3 Schematic diagram of BP neural network optimized by particle swarm optimization algorithm

本節以神經網絡訓練過程中的輸出誤差作為PSO 算法的適應度函數,先隨機地初始化一個粒子群體,每個粒子包含一組神經網絡權值和閾值的數據,通過更新公式不斷迭代每個粒子的取值,最終使得適應度函數值最小。

PSO 算法速度更新如下:

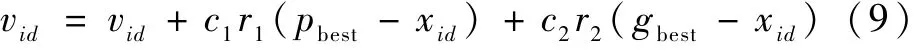
式中:c1、c2為學習因子;r1、r2為(0,1)內的隨機數;pbest為每個粒子當前找到的最優解;gbest為整個種群當前找到的最優解。

PSO 算法位置更新如下:

本節使用的PSO 算法種群數量為50,2 個學習因子均設置為2,迭代步數設置為100。

3 結果與分析

低緯度海洋地區是開展臨近空間低動態飛行器應用的理想場所,本節采用4 個地點的歷史風場數據作為神經網絡的訓練集,坐標分別為

A(112°E,17° N)、B(113° E,9° N)、C(115° E,10°N)、D(116°E,10°N)。 每個坐標點的數據均為250 ×3 652 的數組,其中250 表示高度維,代表在該坐標點250 個不同的高度處取得風場數據,3 652表示時間維,代表每個坐標點有5 年的歷史風場數據,每天0 時和12 時分別采樣,一共3 652 組采樣數據。

3.1 數據降維結果與驗證

利用PCA 法可以求解出風場數據降維后不同階數能夠保留的原始數據信息量比重。 本節以相對模態能量和累積模態能量這2 項指標來衡量模態階數還原原始數據的能力,并根據各階模態能量,選擇合適的降維階數,使得降維后的數據在數據量減小的情況下依然能夠保留大部分風場信息。

以A點數據為例,分析降維數據的數據量降低情況和數據信息保留情況。 考慮到平流層浮空器主要是在20 km 附近持久駐留,因此,需要重點關注該高度附近的風場信息。 該高度附近的風場與10 km 附近的風場有明顯區別,不宜統一使用降維方法進行處理。 為此,提出了分層降維方法,即將整個風場在高度上進行分層處理,即分為2個部分:5 ～15 km 和15 ～30 km。 15 km 以下的區域主要屬于對流層,風場相對較大,且風場隨高度變化較明顯;而15 km 以上的區域風場變化較小。 對這2 部分風場在東西和南北方向上分別開展降維處理并分析得到了如下結果:

他的視線掠過女孩，望向了跟在女孩后面的滑翔翼。它的顏色灰不溜秋的，結構和做工都要粗糙著許多，但它的特殊性，在于它的翼面尤其寬大，比自己的幾乎要寬出二分之一。

1) 東西方向上5 ～15 km:10 階數據保留原數據信息量為99.91%。

2) 東西方向上15 ～30 km:6 階數據保留原數據信息量為99.96%。

3) 南北方向上5 ～15 km:11 階數據保留原數據信息量為99.95%。

4) 南北方向上15 ～30 km:7 階數據保留原數據信息量為99.93%。

3.1.1 東西方向風場降維

由圖4 和圖5 可知,在東西方向上,15 ～30 km的風場特征比較明顯,因此,前6 階模態所包含的能量之和已經達到了99.96%,而5 ～15 km 的風場需要前10 階模態,才能使得能量總和達到99.91%。 可以用5 ～15 km 前10 階的數據和15 ～30 km 前6 階的數據代替原有250 階的數據,將兩部分風場合并后,數據量僅為原有數據量的6.4%。

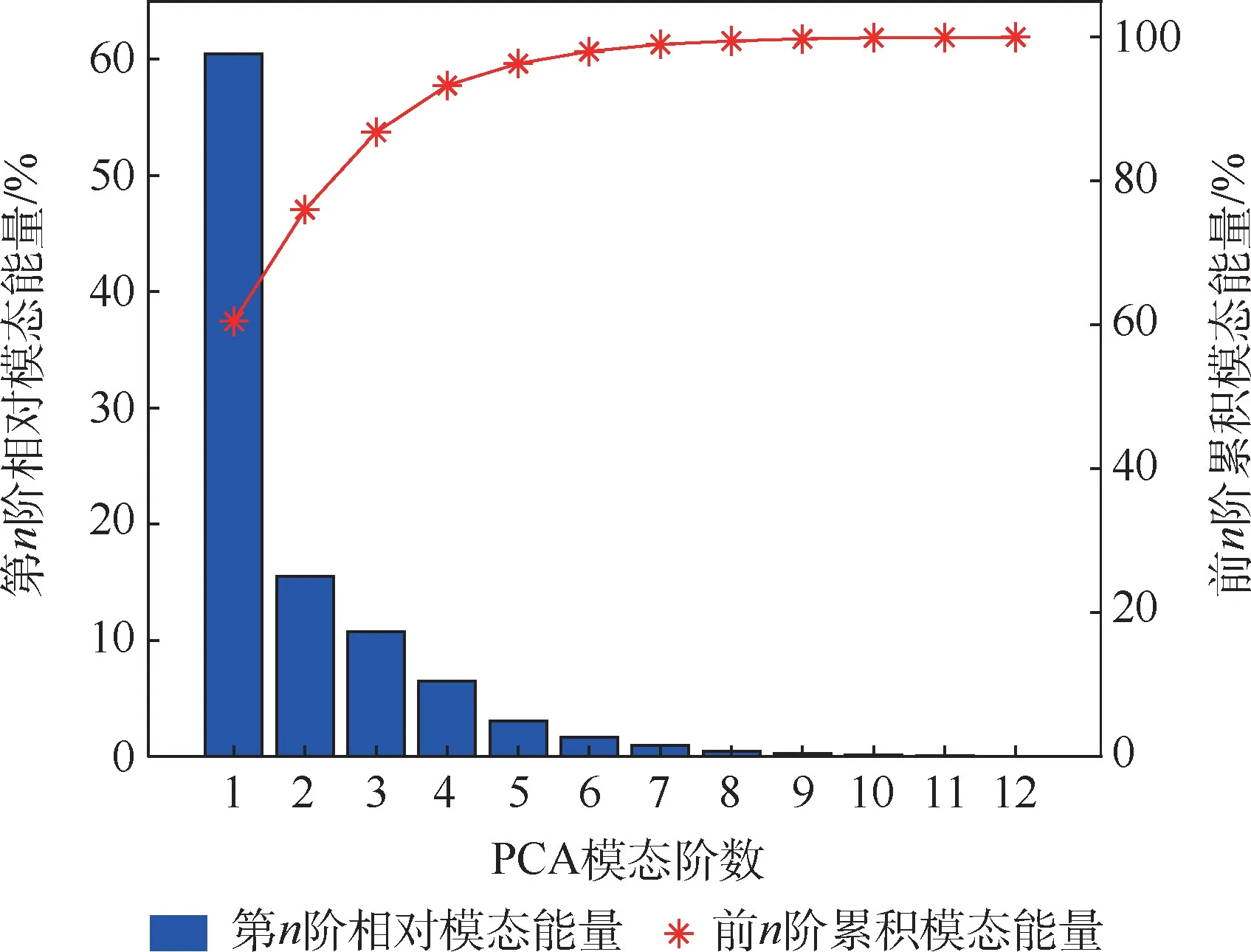
圖4 海拔5 ～15 km 東西方向風場數據降維后的第n 階相對模態能量及前n 階累積模態能量Fig.4 The n-th order relative modal energy and the first n-order cumulative modal energy of east-west wind field data after dimensionality reduction between 5 km and 15 km

圖5 海拔15 ～30 km 東西方向風場數據降維后的第n 階相對模態能量及前n 階累積模態能量Fig.5 The n-th order relative modal energy and the first n-order cumulative modal energy of east-west wind field data after dimensionality reduction between 15 km and 30 km

在PCA 法進行了數據降維處理之后,將降維后的風場數據與實際風場數據進行了對比驗證。由圖6 可知,東西方向降維后的風場與實際風場數據的偏差較小,降維數據基本上與原有數據吻合,高度保留了原有數據的特征。

圖6 東西方向上降維后的風場數據與實際風場數據對比Fig.6 Comparison of east-west wind field data after dimensionality reduction and actual wind field data

3.1.2 南北方向風場降維

由圖7 和圖8 可知,南北方向上兩部分的風場降維數據,即前11 階模態和前7 階模態,所包含的能量之和分別為99.95%和99.93%,南北方向上的風場數據可以用降維后總共18 階的數據來代替原有250 階數據,數據量僅為原有數據量的7.2%。

圖7 海拔5 ～15 km 南北方向風場數據降維后的第n 階相對模態能量及前n 階累積模態能量Fig.7 The n-th order relative modal energy and the first n-order cumulative modal energy of north-south wind field data after dimensionality reduction between 5 km and 15 km

圖8 海拔15 ～30 km 南北方向風場數據降維后的第n 階相對模態能量及前n 階累積模態能量Fig.8 The n-th order relative modal energy and the first n-order cumulative modal energy of north-south wind field data after dimensionality reduction between 15 km and 30 km

由圖9 可知,南北方向降維后的風場與實際風場數據基本吻合。 因此,PCA 法在減小數據量的同時可以保留大部分原有數據的信息。 在后續的神經網絡處理過程中,風場數據就可以使用降維后的數據來代替。

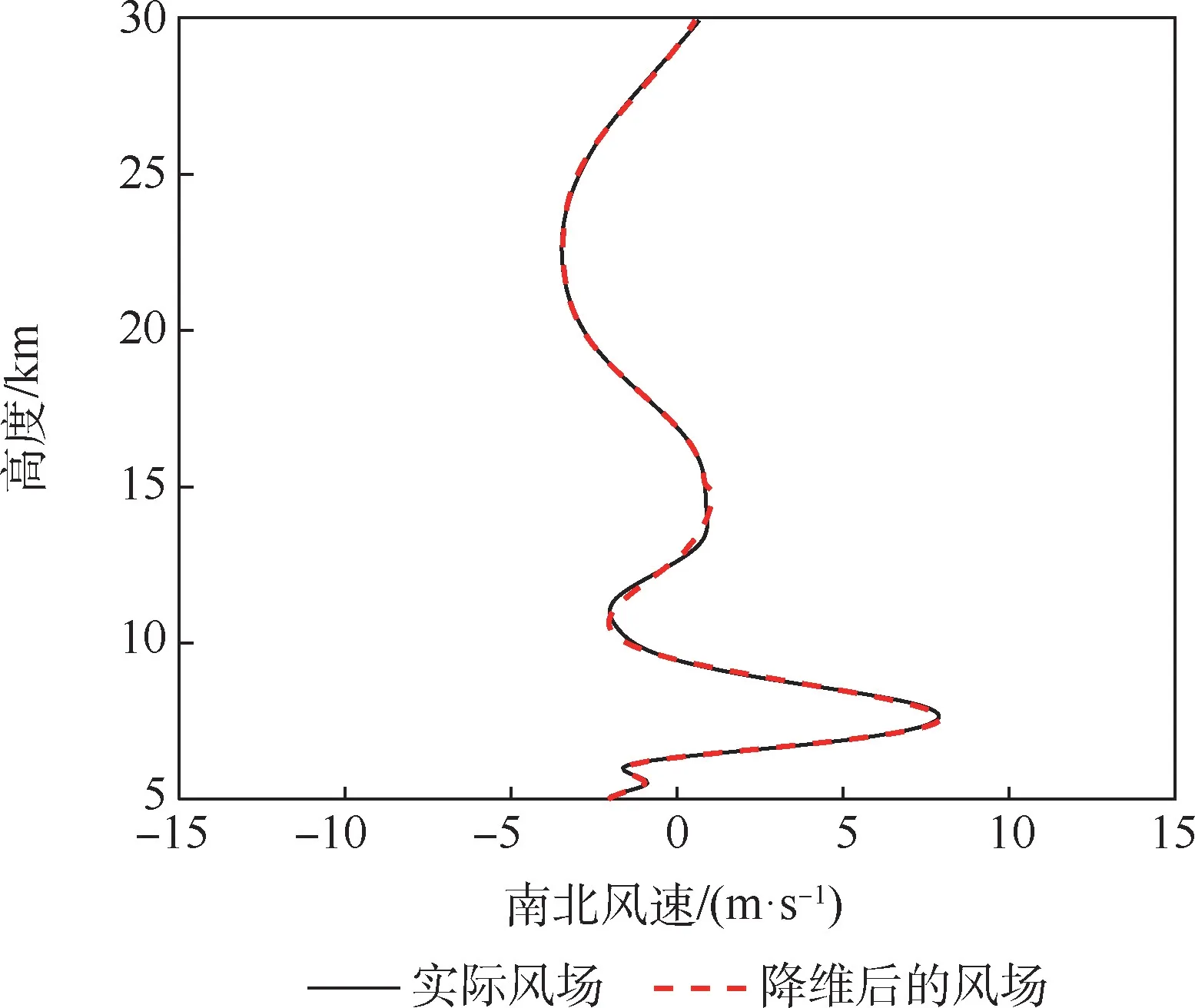
圖9 南北方向上降維后的風場數據與實際風場數據對比Fig.9 Comparison of north-south wind field data after dimensionality reduction and actual wind field data

3.2 神經網絡預測結果分析

根據臨近空間低速飛行器執行任務所需要的工作高度特點[20],使用5 ～30 km 的數據分別對BP 神經網絡和PSO-BP 神經網絡進行訓練,使用訓練后的神經網絡對未來風場進行預測,隨機選取了10 次預測結果與實際風場進行對比。

3.2.1 東西方向風場預測

由圖10 ～圖12 可看出,在東西方向上,BP神經網絡和改進后的PSO-BP 神經網絡均能對風場進行較好的預測,但由于BP 神經網絡采取的是梯度下降算法,偶爾會得到局部最優的結果,使得風場預測結果與實際風場偏差較大;而經PSO算法優化的PSO-BP 神經網絡能夠更好地尋找全局最優值,獲得更好的風場預測效果。2 種預測模型的東西方向風場預報誤差對比分析表明,采用PSO 算法改進后的PSO-BP 神經網絡風場預測模型平均預測誤差要小于BP 神經網絡模型的平均誤差,在15 km 以上區域,二者的平均誤差都小于2 m/s。

圖10 東西方向上BP 神經網絡10 次預測結果與實際風場對比Fig.10 Comparison of 10 prediction results of BP neural network and actual wind field in east-west direction

圖11 東西方向上PSO-BP 神經網絡10 次預測結果與實際風場對比Fig.11 Comparison of 10 prediction results of PSO-BP neural network and actual wind field in east-west direction

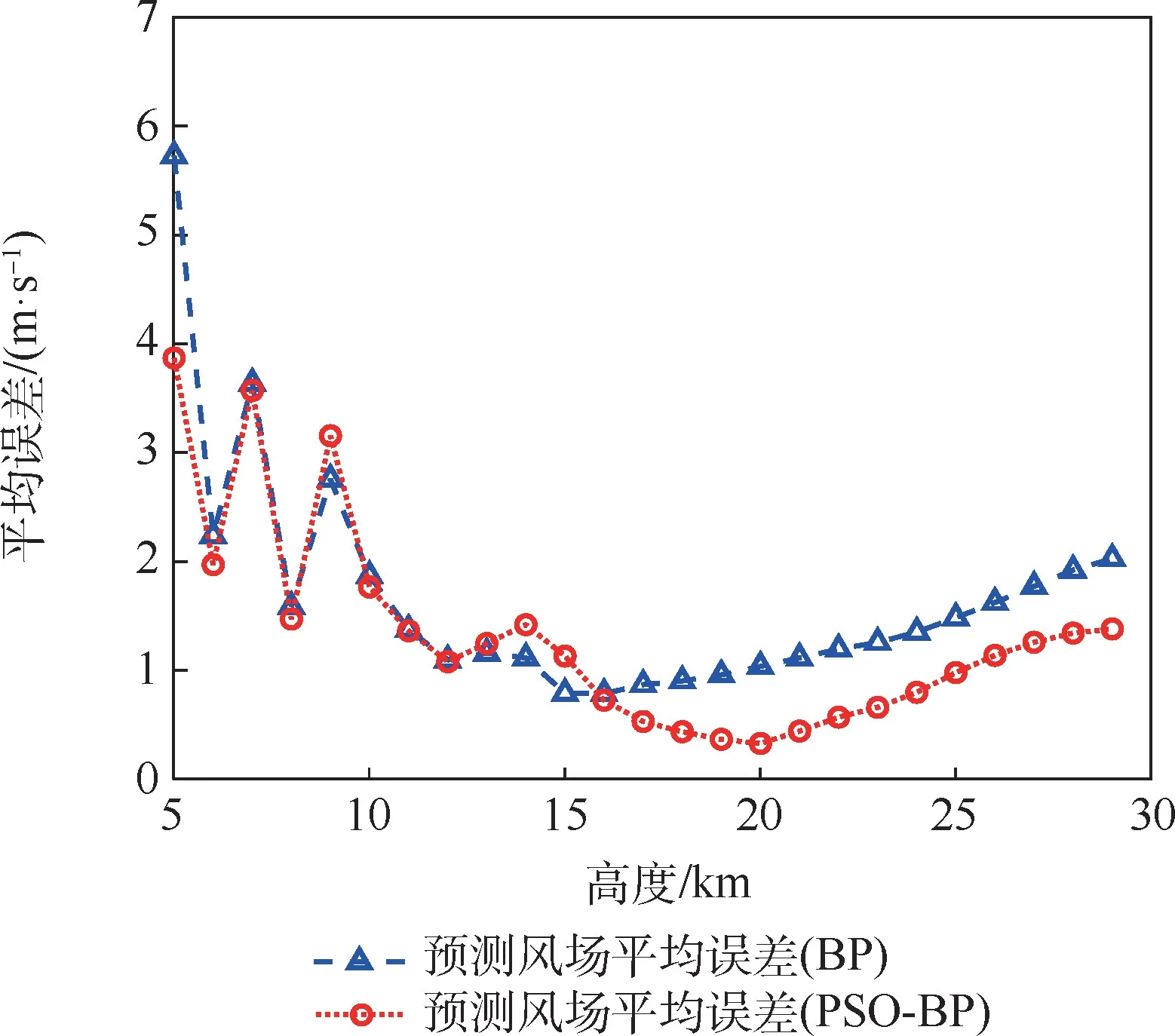
圖12 東西方向上2 種神經網絡10 次預測結果平均誤差對比Fig.12 Comparison of average error of 10 prediction results for two kinds of neural networks in east-west direction

3.2.2 南北方向風場預測

由于平流層獨特的風場環境,其南北方向上的風速分量一般較小,在采用神經網絡對其進行預測時,效果并沒有在東西方向上明顯。 由圖13 ～圖15 可看出,BP 神經網絡和改進后的PSO-BP 神經網絡對南北方向上的風場的預測效果均不如東西方向,但相較于BP 神經網絡,PSO-BP 神經網絡仍然能夠獲得更好的預測效果。

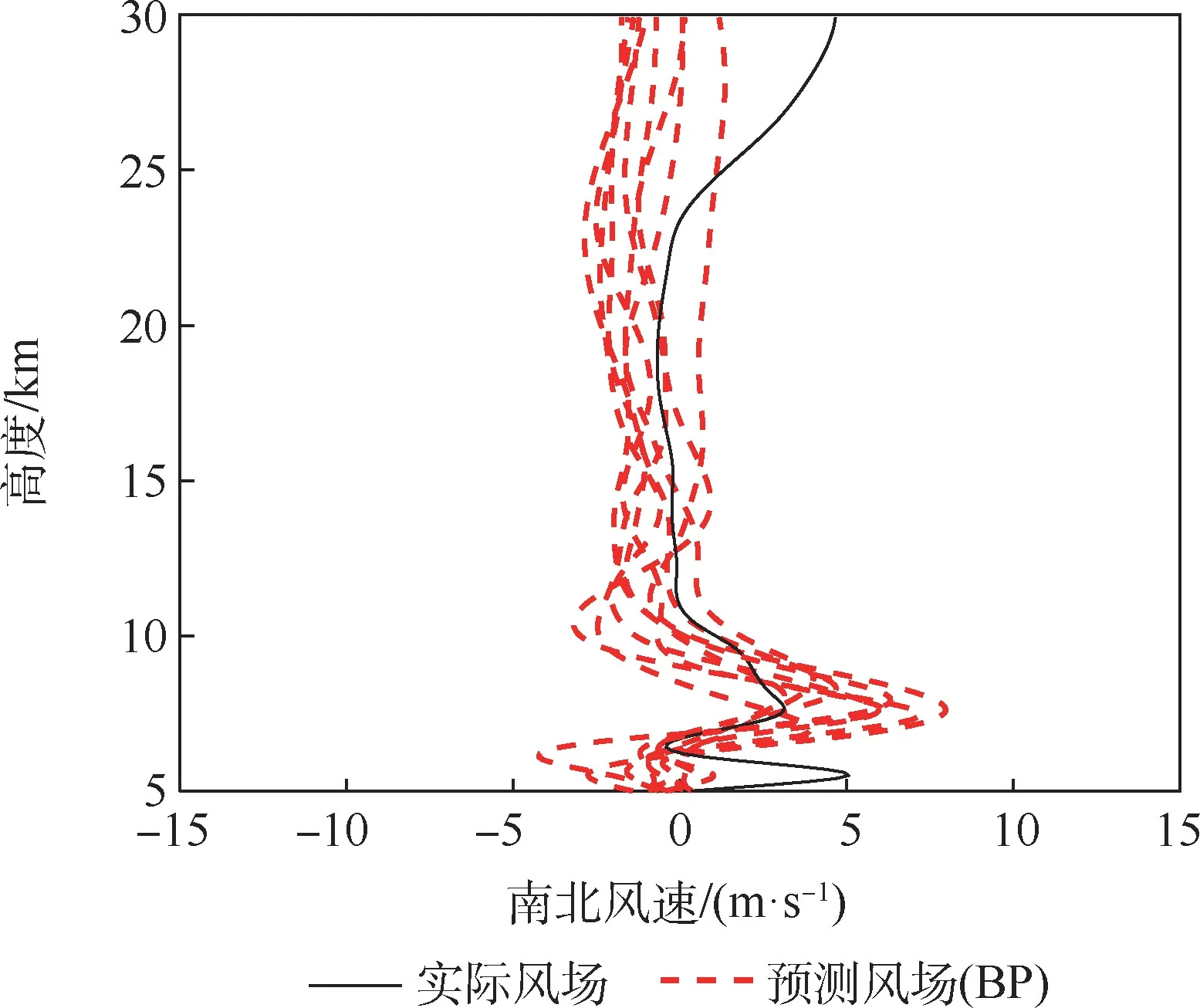
圖13 南北方向上BP 神經網絡10 次預測結果與實際風場對比Fig.13 Comparison of 10 prediction results of BP neural network and actual wind field in north-south direction

圖14 南北方向上PSO-BP 神經網絡10 次預測結果與實際風場對比Fig.14 Comparison of 10 prediction results of PSO-BP neural network and actual wind field in the north-south direction

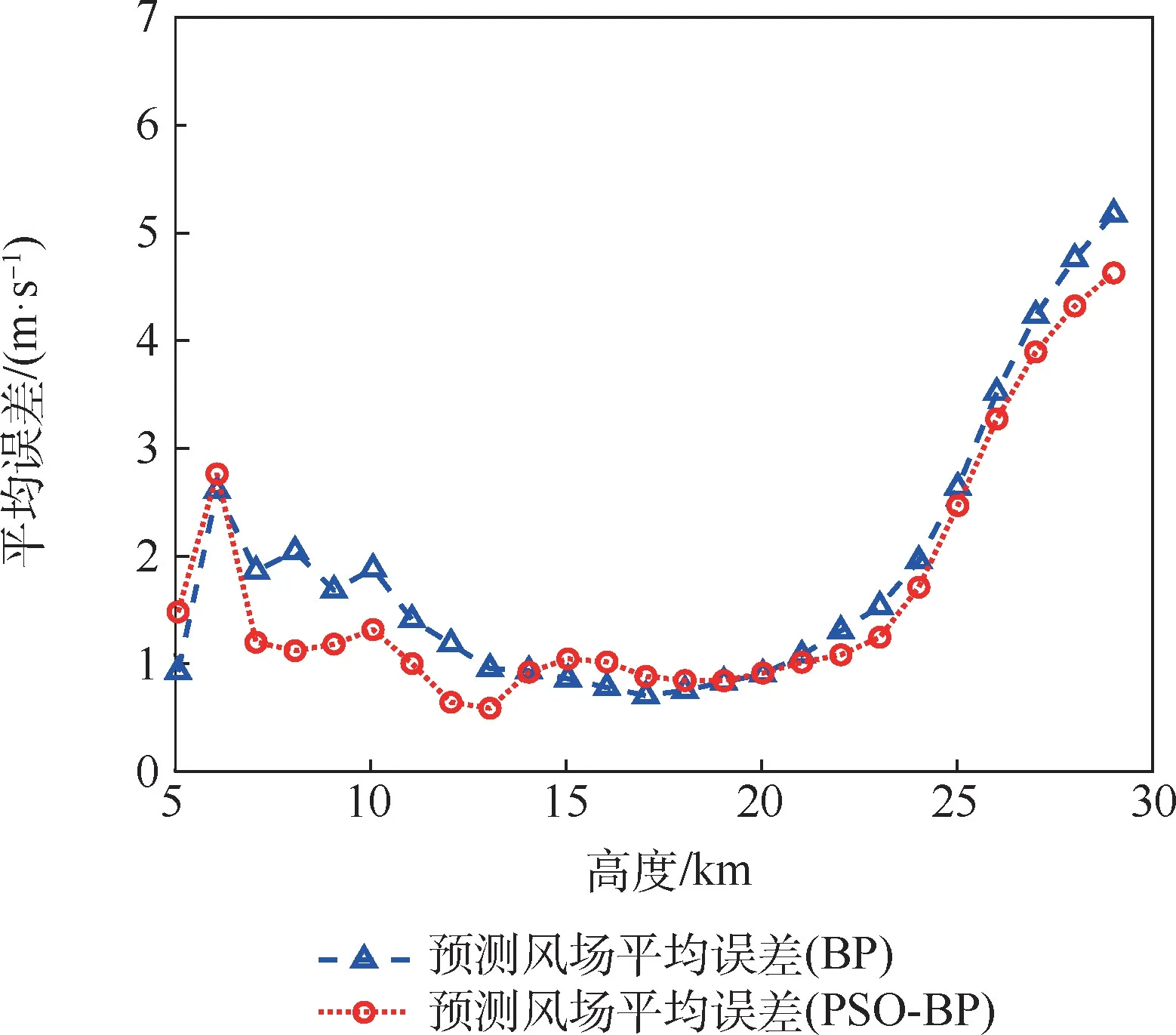
圖15 南北方向上2 種神經網絡10 次預測結果平均誤差對比Fig.15 Comparison of average error of 10 prediction results for two kinds of neural networks in north-south direction

2 種預測模型的南北方向風場預報誤差對比分析表明,在25 km 高度范圍以下的預測效果較好,2 種模型預測結果差異不明顯;在25 km 以上的區域預測2 種模型誤差均快速增加,平均誤差都超過了2.5 m/s。

3.3 區域風場構建分析

平流層飛艇和高空飛機的路徑規劃需要廣大范圍的風場信息,高空氣球區域駐留也并非總是能保持在給定點附近,因此,需要對區域多點風場進行建模。

在使用神經網絡對風場進行預測之后,能夠得到多點隨高度變化的風速數據,本節使用的數據是4 個坐標點A(112°E,17°N)、B(113°E,9°N)、C(115°E,10°N)、D(116°E,10°N)的風場預測結果,用Biharmonic 樣條曲面插值方法對每一高度處的數據進行插值處理,能夠得到三維空間的風速情況。 針對臨近空間低速飛行器典型工作高度20 km 進行風場構建仿真,仿真結果如圖16和圖17 所示。

圖16 東西方向上20 km 高度的區域風速示意圖Fig.16 Schematic diagram of regional wind speed in east-west direction at 20 km

圖17 南北方向上20 km 高度的區域風速示意圖Fig.17 Schematic diagram of regional wind speed in north-south direction at 20 km

由圖16 和圖17 可知,在對風場數據進行插值處理后,任一高度剖面均能得到在不同經緯度的風速變化圖,在平流層浮空器軌跡規劃等問題中,給出任一經緯高坐標,構建的風場模型均能得到風速值在東西方向和南北方向上的分量。 因此,便構建了三維空間的區域風場模型,可以獲取區域內任意點處的風速數據。

臨近空間低速飛行器在執行軌跡規劃或區域駐留任務時,往往需要在較大范圍內飛行。 因此,飛行器在區域風場模型下的軌跡仿真要比單點風場模型下的仿真更符合實際飛行情況。 下面根據平流層飛艇的動力學方程[21]分別在區域風場模型和單點風場模型下仿真飛艇的飛行軌跡。 以坐標原點作為仿真初始點,平流層飛艇在浮力作用下自然升空,海拔高度達到20 km 后降落回收,其飛行軌跡如圖18 所示。

由圖18 可知,在仿真初始階段,區域風場模型和單點風場模型下的飛艇飛行軌跡區別不大。但是,當飛艇逐漸遠離初始點之后,2 種風場模型得到的飛行軌跡便顯現出較大差異,最終二者的水平位移誤差達到了13.3 km。

圖18 兩種風場模型下飛行器的軌跡示意圖Fig.18 Schematic diagram of trajectory for aircraft under two wind field models

4 結 論

1) 采用PCA 法對5 年的歷史風場數據進行降維處理,將250 階的風場數據分別降至16 階和18 階,原始數據信息保留率達到99%以上。 使用降維后組成的新數據代替原有數據,降低了數據量,提高后續工作的計算效率。

2) 采用具有全局尋優特性的PSO 算法改進了易陷入局部最優的BP 神經網絡,并通過改進后得到的PSO-BP 神經網絡和傳統BP 神經網絡對未來風場進行預測。

3) 對2 種神經網絡風場預測模型的預測精度與預測誤差進行了分析,發現相較于基于梯度下降法的BP 神經網絡,經過PSO 算法優化的BP神經網絡訓練得到的神經網絡參數能夠更好地反映風場的變化規律,風場預測精度要高于傳統的BP 神經網絡。

4) 采用Biharmonic 樣條曲面插值方法對單點的神經網絡風場預測結果進行插值處理,構建了一個三維空間的區域風場模型,可以獲取區域內任意點處的風速數據,區域預報可有效提高飛行軌跡仿真結果精度。