兩地中考數學試題的綜合難度比較研究
——以某省C市與H市為例

石玲瑜,王彥棋,謝 瓊

(1.貴州師范大學 數學科學學院,貴州 貴安 新區 550025;2.懷化師范高等專科學校 小學教育學院,湖南 懷化 418000)

0 引言

中考是我國檢測義務教育結果的一個重要方式,也是各所高級中學招生的重要依據,具有測評選拔的功能[1].數學作為義務教育階段的重要學科之一,被大部分學生認為是“最讓人頭疼的科目”,其考試的風向必然使其成為受關注較多的一門學科,所以對中考數學試卷的研究非常必要.《義務教育數學課程標準(2011版)》提出:“合理地設計和實施書面測驗有助于全面考查學生的數學學業成就,及時反饋教學成效,不斷提高教學質量.”[2]而試題難度一直是研究者關注的問題,其中綜合難度系數模型是研究試題難度的重要工具之一.該模型起源于美國學者Nohara提交給美國國家教育統計中心的一份工作報告,在此報告中首次提出了總體難度的概念.2002年,我國學者鮑建生在此基礎上提出了數學學習評價的綜合難度系數模型[3]48,隨后多位研究者利用該模型對課程與試題難度進行國際比較.2013年,周九詩等以中國“人教版”和英國《數學連接》為例對中英初中數學教科書難易程度進行了比較研究[4];2014年,王建磐等選取中國、美國、法國、俄羅斯、澳大利亞的6套高中數學教材,對例題進行了難度因素的水平分析,比較了各教材中例題的難度特征,為我國高中數學教材編寫提供了參考[5];2015年,鄺孔秀等對中、日、韓、新、美、英、法、德、俄、澳10國有代表性的12套小學數學教科書的難度進行了定量分析,為中國小學數學教科書的編寫提出了相關建議[6];2015年,盧建川等對英國數學英才選拔考試MAT的綜合難度進行了分析,為中國數學英才的培育提供了借鑒[7];2018年,武小鵬等對中國與韓國高考數學試題綜合難度的比較研究,為中國高考試題的命制提供了參考[8];2020年,張玉環等基于2015～2019年中國和法國高考數學試卷在綜合難度視角下的比較研究,提出了關于新高考的命題建議[9].近年來,對于國內試題綜合難度系數的研究也是層出不窮,但對于中考試題綜合難度的研究較少,大多是對高考卷的研究,比如:張怡等基于綜合難度系數模型的新高考數學試題評價研究[10];劉清等對核心素養視角下的高考試題難度進行探析[11];劉菲菲等對近5年高考數學全國卷(理科)數列試題難度的分析等[12]51.本研究在鮑建生教授的綜合難度系數模型的基礎上,對某省C市與H市近5年的中考試題進行對比分析,以期為各地對中考試題難度的把控提供參考.

1 研究設計

1.1 研究對象

分別選取C市與H市2017～2021年中考數學試卷作為研究對象,共10套,所有試卷的題型都只包含選擇題、填空題和簡答題.其中,C市2017～2019年這三年中考試題數均為26道,2020年與2021年試題數均為25道;而H市只有2019年試題數為23道,其他4個年份試題數均為24道.

1.2 研究工具

鮑建生等構建的綜合難度系數模型中難度因素的水平劃分如表1所示[3]49.本研究在此基礎上進行了適當的修訂,將“探究”這一因素改名為“認知水平”,并將水平四“探究”去掉,該因素只保留識記、理解、應用3個水平;將“背景”也只分成無背景、生活背景及科學背景3個水平;通過整理試題發現,所研究的10套試卷中涉及符號運算較少,因此“運算水平”中不考慮符號與數值運算的區別,并將“運算水平”分為無運算、簡單運算及復雜運算;由于近幾年對學生數學閱讀能力的關注越來越多,閱讀能力是學生可持續發展能力的一個重要標志[13],所以本研究增加了“閱讀量”這一因素.

表1 綜合難度因素的水平劃分

綜上所述,本研究將影響試題綜合難度的因素修訂為:認知水平、背景、運算水平、推理水平、知識含量及閱讀量.基于中考試題的綜合難度系數模型結構與內涵見表2[12]52(2頁).根據表2的綜合難度系數框架,建立各因素的難度系數模型

表2 基于中考試題的綜合難度系數模型結構與內涵

其中:d i(i=1,2,3,4,5)表示不同的維度;d ij表示第i個維度中第j個水平的權重(根據不同的水平分別取1,2,3,…);nij表示本組題目中屬于第i個維度中第j個水平的題目數;n表示本組題目的總個數[3]50.

1.3 數據收集與處理

利用以上的綜合難度系數模型對C市與H市共10套試卷進行分析.為方便分析,將C市的中考試卷用“C卷”表示,H市的中考試卷用“H卷”表示.下面以2道試題為例進行分析,根據6個難度因素系數的水平進行賦值.

例1(2018年C市第9題)我國南宋著名數學家秦九韶的著作《數書九章》里記載有這樣一道題目:“問有沙田一塊,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知為田幾何?”這道題講的是:有一塊三角形沙田,三條邊長分別為5里、12里、13里,問這塊沙田面積有多大?題中的“里”是我國市制長度單位,1里=500米,則該沙田的面積為().

A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方干米

本題認知水平為理解、背景為科學背景、運算水平為簡單運算、推理水平為一般推理、知識含量為2個知識點、閱讀量為＞100個字符,其賦值情況如表3所示.

表3 例1難度因素賦值情況

例2(2021年H市第22題)如圖1,在半徑為5 cm的☉O中,AB是☉O的直徑,CD是過☉O上一點C的直線,且AD⊥DC于點D,AC平分∠BAD,E是BC的中點,OE=3 cm.

(1)求證:CD是☉O的切線;

(2)求AD的長.

本題有2個小問,難度因素水平按最高的水平計算,其中知識含量與閱讀量為2個小問的和,本題認知水平為應用、背景為無背景、運算水平為簡單運算、推理水平為一般推理、知識含量為多個知識點、閱讀量為50～100個字符,其賦值情況如表4所示.

表4 例2難度因素賦值情況

按照表2中的難度系數模型結構與內涵對C市與H市中考試題進行如例1與例2的賦值,通過公式(1)計算出綜合難度系數.由于篇幅有限,將最終形成的原始數據整理計算后得到表5(4頁).

2 研究結果

根據表5的統計結果,下面對C市與H市2017～2021年中考數學試題在認知水平、背景、運算水平、推理水平、知識含量與閱讀量6個難度因素上進行分析比較,最后通過綜合難度模型雷達圖對因素進行對比說明.

表5 2017～2021年C市與H市中考數學試題綜合統計[14]

2.1 認知水平

在認知水平因素上的統計結果如圖2所示.

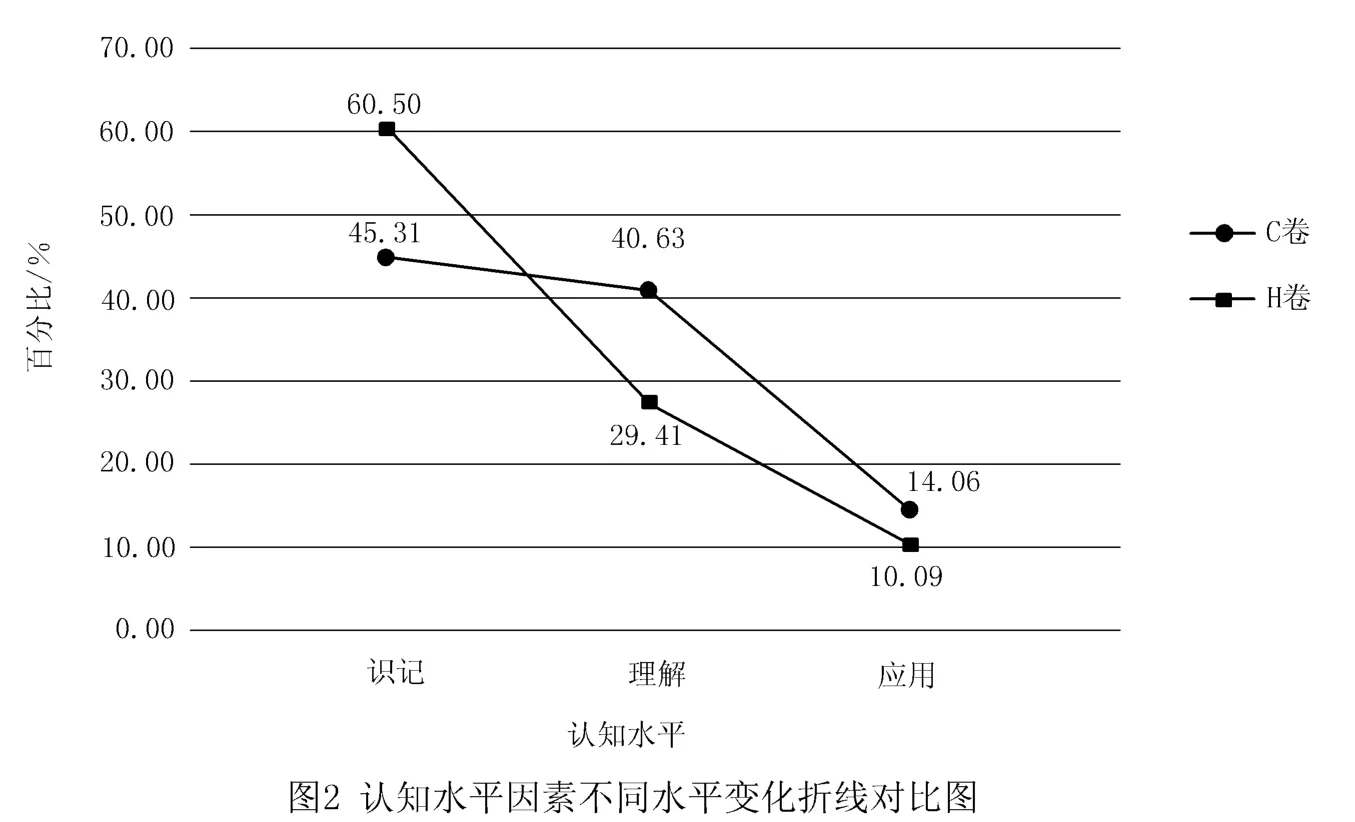
根據圖2可知,2套試卷認知水平的比例隨著水平層次的提高而依次遞減.H卷識記水平的試題數占一半以上,而應用水平的試題數僅占總試題數的10.09%.C卷理解水平與應用水平的試題數占總試題數的54.69%,說明C卷的大部分試題需要對知識點進行理解與綜合分析才能解答.C卷識記水平的試題數少于H卷,而理解水平與應用水平的試題數均多于H卷,這說明C卷重在考查對知識點的靈活運用.

2.2 背景

在背景因素上的統計結果如圖3所示.

根據圖3可知,H卷的無背景試題數占75.63%,科學背景試題在近5年的所有試卷中只出現了1道,僅占0.84%.C卷的無背景試題數也占據總試題數的很大一部分,有背景的試題數占32.03%,其中以生活背景為主,占29.69%.總體來看,C卷含背景的試題數要多于H卷,無論是含生活背景的試題數還是含科學背景的試題數均多于H卷.從數據統計的結果可以看出,2套試卷都重視對數學知識本身的考查,涉及背景的試題較少,尤其涉及考查科學背景的試題更是微乎其微.

2.3 運算水平

在運算水平因素上的統計結果如圖4所示.

根據圖4可知,H卷簡單運算占58.82%,復雜運算只占8.40%,其他的試題均不需要進行運算,說明H卷對于運算能力的考查集中于簡單的基礎運算.C卷涉及運算的試題占76.56%,其中簡單運算占62.50%,說明C卷也是重在考查學生的基本運算能力.C卷的復雜運算水平試題數約是H卷復雜運算水平試題數的2倍,而對于無運算的試題數,H卷要多于C卷,這足以說明就運算水平而言,C卷的難度明顯高于H卷.

2.4 推理水平

在推理水平因素上的統計結果如圖5所示.

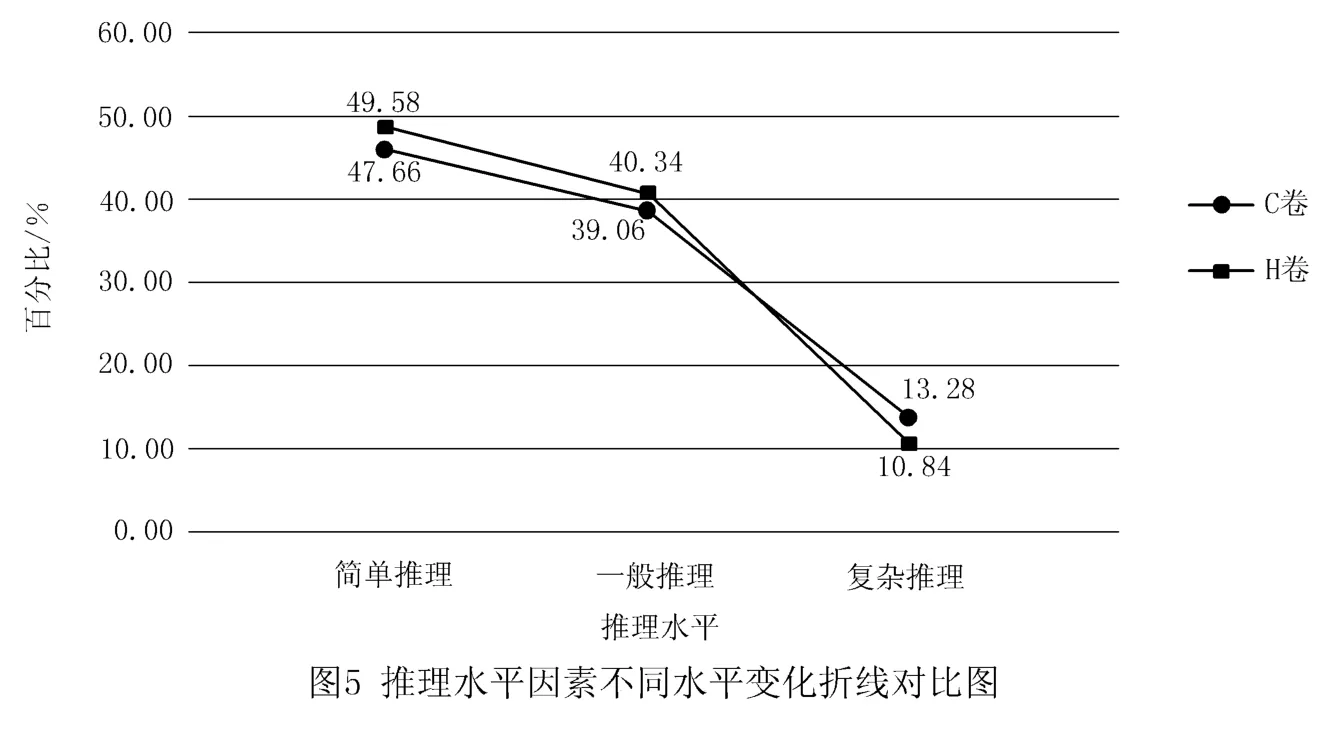
根據圖5可知,2套試卷對于推理水平的考查都是隨著水平的提高而依次減少,而且3個水平的考查所占比例差不多.H卷考查簡單推理水平的試題數約占總試題數的一半,考查一般推理水平的試題數占40.34%,考查復雜推理水平的試題數僅占10.84%.C卷在簡單推理與一般推理的考查上試題數均略少于H卷,而考查復雜推理水平的試題數占13.28%,高于H卷.總體來看,兩者考查簡單推理水平與一般推理水平的試題數總和都接近90%,即考查復雜推理的試題數較少,更多偏重考查學生對于基礎知識的掌握情況.

2.5 知識含量

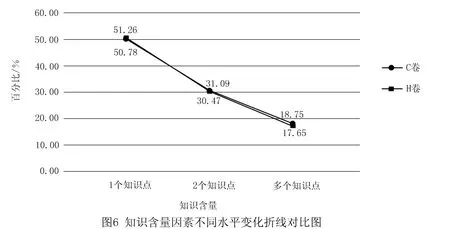
在知識含量因素上的統計結果如圖6(6頁)所示.

根據圖6可知,兩條折線幾乎重合,說明H卷與C卷在知識含量的考查上區別不大,都集中在1個知識點這一水平上,占據整套試題的一半以上,對于多個知識點的考查較少.H卷在1個知識點與2個知識點水平上的試題數均略多于C卷,而在多個知識點這一水平上的試題數略少于C卷.

2.6 閱讀量

在閱讀量因素上的統計結果如圖7所示.

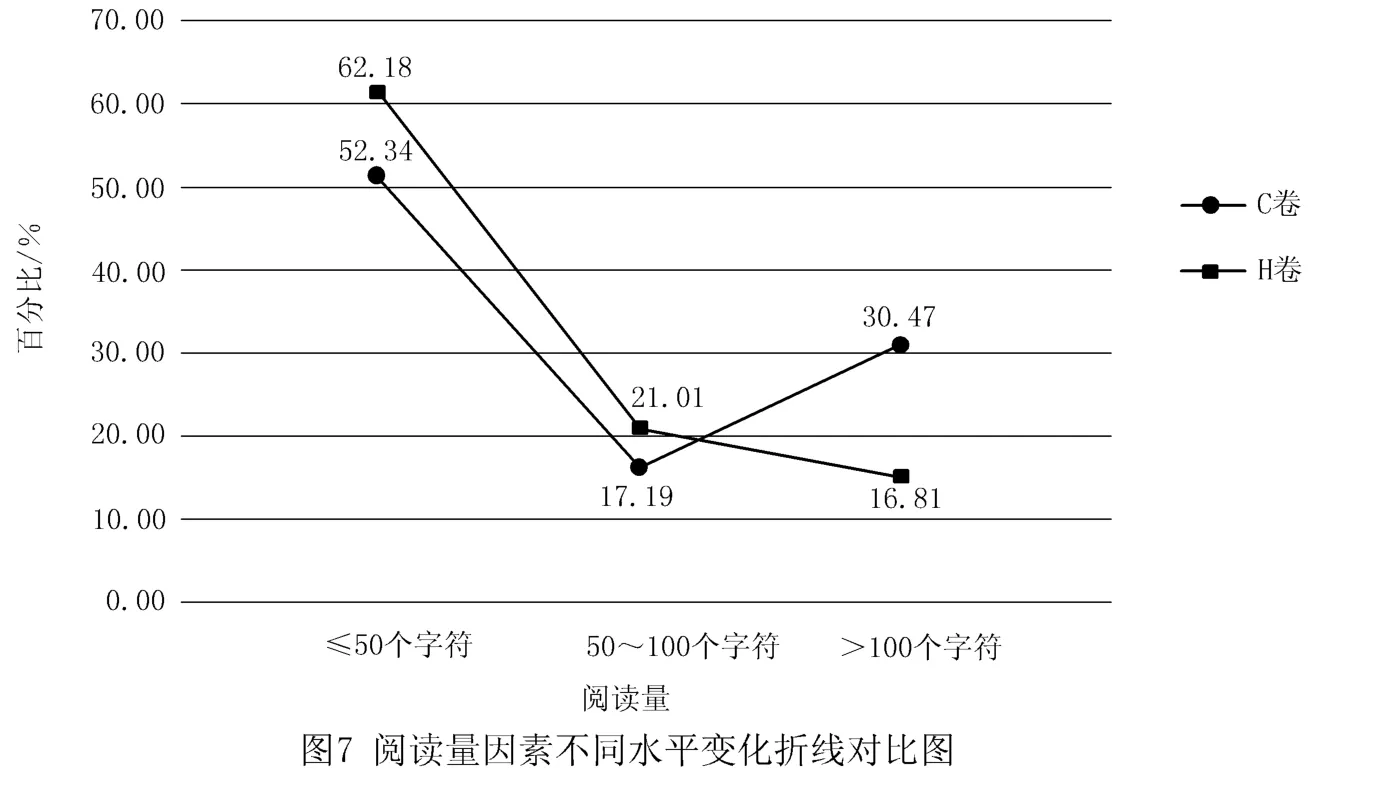
根據圖7可知,H卷≤50個字符的試題數占62.18%,說明大部分試題的閱讀量水平較低,＞100個字符的試題數只占16.81%.C卷≤50個字符的試題數相較于H卷少,處于第二水平的閱讀量也低于H卷,而＞100個字符的試題數接近H卷 的2倍,說 明C卷的閱讀量水平比H卷的閱讀量水平高.總體來看,處于第二水平,即字符數在50～100個之間的試題數最少,說明2套試卷的閱讀量水平均不高.

2.7 綜合難度分析

表5是通過公式(1)計算出的6個難度因素各自的難度系數,根據表5中的數據得到C市與H市中考數學試題不同因素綜合難度系數的雷達圖,如圖8所示.

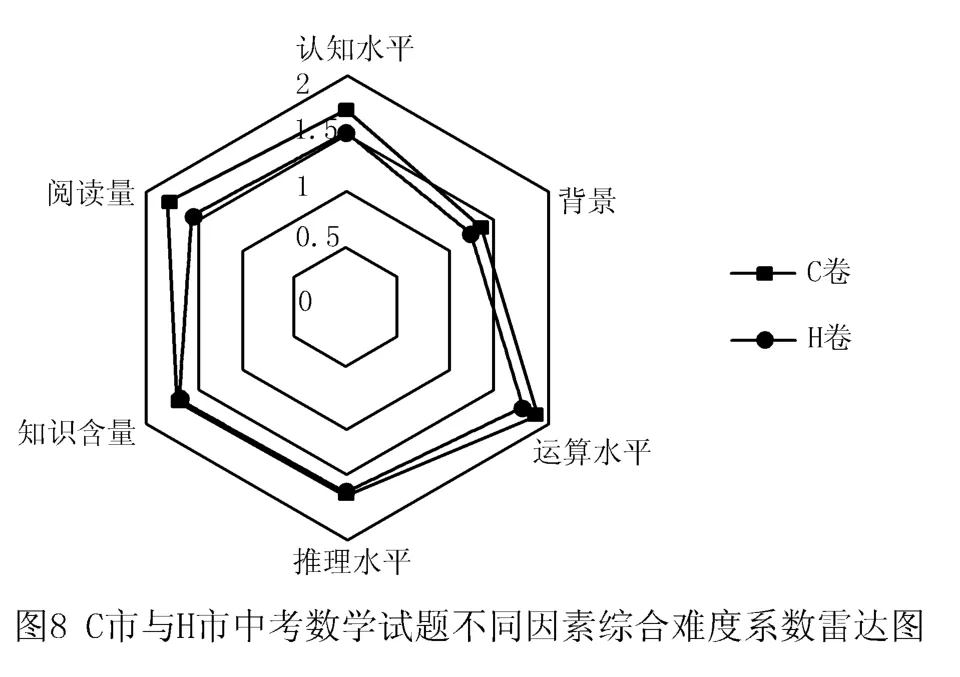
由圖8可以看出,C卷與H卷在整體難度上相近,但在各難度因素上還是有差異的.在認知水平、運算水平與閱讀量3個因素中,C卷的難度系數比H卷的難度系數高出大約0.2;在推理水平與知識含量2個因素中,兩者之間的差異微乎其微,表現出一致性;在背景因素中,C卷的難度系數大于H卷的難度系數,說明C卷更加注重在數學試題中添加背景.由以上分析可以看出,C卷的6個難度因素系數均高于H卷,這足以說明C卷的難度大于H卷.但是,本研究只考慮了影響試題難度的6個因素,而影響試題綜合難度的因素肯定不止這6個,因此這些數據僅成立于綜合難度系數模型這一理論下.

3 結論與建議

3.1 研究結論

3.1.1 C卷與H卷試題在閱讀量因素上有明顯的差異,C卷更注重考查學生的數學閱讀能力

根據圖7可以看出,C卷字符數多于100個的試題數比例遠遠大于H卷.通過分析試卷發現,字符數較多的試題往往含有背景,僅考查純數學知識的試題一般字符數較少.由背景因素的相關數據可以得出,C卷涉及生活背景與科學背景的試題明顯多于H卷,在試題中添加背景目的就是讓學生明白數學在實際生產生活中的作用,而背景的添加需要文字的描述,這就自然而然地增加了題目的閱讀量.

3.1.2 H卷認知水平的難度較低,注重對學生識記水平的考查

根據表5與圖2的數據統計結果可知,H卷識記水平的試題比例偏高,只要學生能記住相關概念、公式或者法則就可得出答案,不需要對相關知識點進行理解與分析;而理解水平的試題數只占識記水平試題數的一半:由此可以看出,H卷在不同認知水平的試題數不太均衡,這可能與當地的教育水平有一定的關系,H市的教育水平相對落后,出卷人也會考慮學生的實際情況.雖然杜絕在考試中出現繁難偏雜的“怪題”,但是試題過于簡單,就會失去“數學味”.而C卷識記水平與理解水平的試題比例約為1∶1,可以看出C卷重在考查這2個水平.中考是由各市自主命題,如果只考慮當地學生的實際情況,那么中考過后學生面臨的將是與全國各地的學生進行競爭,所以提高當地的教育質量才是關鍵,而不是一味地降低考試難度.

3.1.3 C卷6個因素的難度系數均高于H卷,即C卷的綜合難度高于H卷

研究結果顯示,C卷6個因素的難度系數都比H卷的難度系數高,這意味著C卷每一個因素的考查水平都高于H卷,即C卷難于H卷.C市屬于該省的省會城市,擁有全省最好的教育資源,學生的綜合水平要高于H市學生的綜合水平,所以這一結果也符合當前的教育現狀.尤其是認知水平、運算水平及閱讀量這3個因素上,C卷明顯高于H卷.從各因素不同水平變化折線對比圖來看,C卷在各因素不同水平的出題比例上也優于H卷,試卷的結構更加合理.H卷在各因素不同水平的出題比例上應該有所優化,比如含有背景的題目較少,應該將實際生產生活融入到試題中.

3.2 命題建議

3.2.1 均衡各難度因素,優化試卷質量

C卷除了背景這一因素外,其他5個因素的難度相差不大,具有一定的平衡性,總體來看均衡性表現不錯.但是,H卷在認知水平、背景與閱讀量3個因素上的難度系數明顯小于其他幾個因素.在編制試題時,應該綜合考慮各難度因素對試卷總體難度的影響程度,這樣才能更好地凸顯中考的評價與選拔功能.各地區自主命題賦予了地方更多選拔人才的權利,所以各地也應該充分考慮本地區的教育水平,了解本地區不同層次的人對中考試題的需求,同時也要學習其他地區在試題編制上的優點.目前,教育者十分重視學生數學核心素養的形成,所以考試命題要緊跟教育趨勢,充分考慮各因素在核心素養形成過程中所起的不同作用,均衡各難度因素,優化試卷質量[15].

3.2.2 豐富試題背景,貼近實際生活

充分考慮初中生的年齡特點,結合其認知能力在試題中編入適當的背景,從而使他們對數學能有更好的認知.由本研究的統計數據可見,目前中考試題的編制對背景的應用有所欠缺.初中階段所學習的數學知識絕大部分來源于生活并應用于生活,在考題中融入生活情境可以讓學生更加深刻地體會這一點.本研究將科學背景的內涵定義為以數學文化為背景或涉及其他學科.2套試卷中涉及科學背景的試題極少,說明這兩個地區對于數學文化的教學不夠重視,或者在考題編制時忽視了數學文化的滲透;沒有凸顯學科之間的聯系,在中考命題中融入其他學科的相關內容,會使學生了解到各學科之間是相互關聯的.只有將數學知識的考查添加適當的背景,在日常教學過程中教師才會更加注重將數學與實際生產生活聯系起來,從而激發學生學習數學的興趣.

3.2.3 創新題型設置,培養思維能力

通過對兩個地區近5年中考試題的分析發現,試題的類型都是“循規蹈矩”,具有創新性的試題少之又少.國家大力提倡培養創新型人才,而創新能力是需要通過教育去培養的,如果我們用來評價學生學習效果的試題都是幾十年如一日,在題型和內容上沒有新的突破,表現出千篇一律的風格,那么學生的思維能力又如何能得到提高.近幾年,還是有一部分教育研究者意識到了這一點,總體趨勢在向著好的方向發展,很多地方的中考試卷出現了開放性的試題,包括一些游戲與活動等,這些元素的融入可以活躍學生的思維.

3.3 研究不足

綜合難度系數的影響因素很多且較為復雜,除了本研究中所提到的6個因素,呂世虎等人還提出了試題量、試題難度分布、試卷新穎性等因素[16],所以本研究存在一定的局限性,還有待進一步的完善.在各難度因素水平的確定過程中,會存在一定的主觀性,這會導致研究結果存在誤差,但對研究結果的影響不大.