重視“閱讀材料”，挖掘潛在價(jià)值
——以滬教版普通高中數(shù)學(xué)新教材為例

龐良緒

上海市市西中學(xué) 200040

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》將“閱讀自學(xué)”作為數(shù)學(xué)教學(xué)活動(dòng)之一，明確了“數(shù)學(xué)閱讀教學(xué)”在高中數(shù)學(xué)教學(xué)中的重要性，同時(shí)又指出“通過在高中階段數(shù)學(xué)文化的學(xué)習(xí)，學(xué)生將體會(huì)數(shù)學(xué)的科學(xué)價(jià)值、應(yīng)用價(jià)值、人文價(jià)值，尋求數(shù)學(xué)進(jìn)步的歷史軌跡，受到優(yōu)秀文化的熏陶，領(lǐng)會(huì)數(shù)學(xué)的美學(xué)價(jià)值”.基于此，現(xiàn)行滬教版普通高中數(shù)學(xué)新教材中融入了“章頭圖與引言”“探究與實(shí)踐”“課后閱讀”“內(nèi)容提要”等閱讀材料.這些閱讀材料是教材的重要組成部分，是對(duì)教材正文的補(bǔ)充和延伸，為學(xué)生提供了豐富的具有思想性、可讀性、趣味性、應(yīng)用性的反映數(shù)學(xué)本質(zhì)的素材，豐富了教材內(nèi)容，提高了學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，拓展了學(xué)生的數(shù)學(xué)活動(dòng)空間，實(shí)現(xiàn)了“人人都能獲得良好的教育，不同的人在數(shù)學(xué)上得到不同的發(fā)展”，全面提升了學(xué)生數(shù)學(xué)學(xué)科核心素養(yǎng).本文以滬教版普通高中數(shù)學(xué)新教材中的部分閱讀材料為例，充分挖掘其潛在的價(jià)值，并試著對(duì)新教材閱讀材料的分類與特點(diǎn)以及閱讀材料的教學(xué)現(xiàn)狀加以分析，旨在重視和凸顯教材中閱讀材料的價(jià)值.

新教材閱讀材料的分類與特點(diǎn)

為了挖掘閱讀材料的價(jià)值，根據(jù)其內(nèi)容特點(diǎn)，對(duì)新教材閱讀材料大致可分為以下幾類：

（1）拓寬知識(shí)類：對(duì)課本已有的數(shù)學(xué)知識(shí)進(jìn)一步拓展延伸，如“調(diào)和平均值與算術(shù)平均值不等式”“三次方程求根公式與復(fù)數(shù)的起源”等，都是關(guān)于公式的推廣與加強(qiáng).

（2）學(xué)科交叉類：利用數(shù)學(xué)公式或模型解決相關(guān)學(xué)科中的問題，可作為學(xué)生跨學(xué)科融合學(xué)習(xí)的教育載體，如物理學(xué)中的“圓周運(yùn)動(dòng)與簡(jiǎn)諧振動(dòng)”“宇航員的訓(xùn)練”“火箭速度的計(jì)算公式”等.

（3）數(shù)學(xué)史類：介紹數(shù)學(xué)家的生平事跡、貢獻(xiàn)以及他們?yōu)榱私?shù)學(xué)概念、定理經(jīng)歷的曲折歷程，如“對(duì)數(shù)簡(jiǎn)史”“函數(shù)概念的形成與發(fā)展”等.

（4）探究學(xué)習(xí)類：從課本中的公式、定理入手，通過類比、聯(lián)想探究得到新的結(jié)論，如“利用等式證明不等式”“冪函數(shù)、指數(shù)函數(shù)與對(duì)數(shù)函數(shù)增長(zhǎng)速度的比較”等.

通過上述分類，可以發(fā)現(xiàn)閱讀材料涵蓋的范圍比較廣泛，其特點(diǎn)主要表現(xiàn)在：是教材正文的有機(jī)組成部分，是了解數(shù)學(xué)史、拓寬知識(shí)面、進(jìn)行思想品質(zhì)教育的極好素材；同日常的生產(chǎn)生活緊密聯(lián)系，具有廣泛的應(yīng)用性；是開展探究性、研究性學(xué)習(xí)的重要載體；還具有數(shù)學(xué)美、趣味性、時(shí)代性、可加工性等特點(diǎn).

教師作為課堂教學(xué)的主導(dǎo)者，對(duì)閱讀材料的關(guān)注程度直接影響著教學(xué)觀念的形成和教學(xué)目標(biāo)的達(dá)成.因此，教師應(yīng)認(rèn)真研讀閱讀材料，讓學(xué)生在閱讀之前，做到“心中有數(shù)”，充分理解閱讀材料設(shè)計(jì)的指導(dǎo)思想和意圖，對(duì)其教育功能有足夠的認(rèn)識(shí)，發(fā)揮其應(yīng)有的潛在價(jià)值.

教材中閱讀材料的教學(xué)現(xiàn)狀

斯托利亞爾說過，“語言學(xué)習(xí)離不開閱讀”.而數(shù)學(xué)教學(xué)也就是數(shù)學(xué)語言教學(xué)，所以數(shù)學(xué)學(xué)習(xí)離不開閱讀.閱讀材料蘊(yùn)含豐富的數(shù)學(xué)思想方法，為教與學(xué)提供了豐富的素材，也為教師從單純的傳授知識(shí)向提升學(xué)生的綜合素養(yǎng)提供了載體.然而，在實(shí)際的課堂教學(xué)中，有些教師沒有意識(shí)到數(shù)學(xué)閱讀材料的價(jià)值，認(rèn)為閱讀材料是學(xué)生的課外讀物，閱讀材料往往被其忽略，成了一種擺設(shè)，甚至閱讀材料無人問津，成了被遺忘的角落.

造成閱讀材料被忽視的主要原因在于：一是現(xiàn)行的教科書或教師用書沒有給閱讀材料明確的教學(xué)要求，沒有把閱讀材料納入教學(xué)內(nèi)容，在教學(xué)安排中也沒有規(guī)定具體的課時(shí)數(shù)；二是部分教師由于受傳統(tǒng)應(yīng)試教育的影響，存在主觀意識(shí)的偏見，認(rèn)為閱讀材料只是可有可無的裝飾品，不是課堂教學(xué)的重點(diǎn)，教師過度關(guān)注學(xué)生的成績(jī)，認(rèn)為學(xué)習(xí)閱讀材料對(duì)數(shù)學(xué)成績(jī)的提高沒有多大幫助，對(duì)應(yīng)試教育沒有實(shí)際作用，不愿意在課堂上花時(shí)間與學(xué)生進(jìn)行交流、探究；三是有些閱讀材料片面追求一些“時(shí)髦”或“高級(jí)”的東西，同教材正文聯(lián)系不夠緊密，閱讀材料難度偏大，且知識(shí)性、趣味性不夠，不顧學(xué)生的實(shí)際接受能力，反而會(huì)降低學(xué)生的閱讀興趣，不利于提高學(xué)生的綜合素養(yǎng).

正是以上種種原因，閱讀材料沒有發(fā)揮其應(yīng)有的教育教學(xué)功能，要想突破這一瓶頸，需要教育管理者、教材編寫者、師生的一道努力，尤其需要一線的中學(xué)教師創(chuàng)造可應(yīng)用的閱讀材料.在平時(shí)的課堂教學(xué)中，教師應(yīng)形成一套具有可操作性、能靈活使用閱讀材料的方法，比如與正文穿插講解，讓生生合作交流，學(xué)生有問題可以向教師請(qǐng)教，學(xué)生學(xué)習(xí)知識(shí)的同時(shí)，培養(yǎng)合作學(xué)習(xí)的習(xí)慣；鼓勵(lì)學(xué)生撰寫小論文，如研究性課題等.

教材中閱讀材料的潛在價(jià)值

閱讀材料編入教材增加了教學(xué)內(nèi)容的彈性，使教材更符合不同層次學(xué)生的發(fā)展需要.比如，利用閱讀材料進(jìn)行探究性學(xué)習(xí)，在問題解決過程中培養(yǎng)探究意識(shí)，提高學(xué)生解決問題的能力；再如，利用閱讀材料滲透數(shù)學(xué)人文理念，對(duì)學(xué)生進(jìn)行精神滋養(yǎng)和文化熏陶，提升數(shù)學(xué)的育人功效.在課堂教學(xué)中，教師應(yīng)根據(jù)閱讀材料的特點(diǎn)、學(xué)生的接受能力以及實(shí)際的教學(xué)需求，采取相應(yīng)的教學(xué)方式，充分挖掘其潛在的價(jià)值.

1.借助閱讀材料，開展探究活動(dòng)

蘇霍姆林斯基說過，“在人的內(nèi)心深處，都有一種根深蒂固的需要，那就是希望自己是一個(gè)發(fā)現(xiàn)者和探索者”.《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》也指出：高中數(shù)學(xué)課程應(yīng)力求通過各種不同形式的自主學(xué)習(xí)、探究活動(dòng)，讓學(xué)生體驗(yàn)數(shù)學(xué)發(fā)現(xiàn)和創(chuàng)造的歷程.基于此，滬教版教材給出了相關(guān)的閱讀材料，比如探究公式、定理、結(jié)論的產(chǎn)生過程，在問題解決的過程中，體會(huì)前人是如何提出問題、解決問題的.對(duì)這些閱讀材料的研讀，學(xué)生既可以重溫前人對(duì)數(shù)學(xué)知識(shí)探索發(fā)現(xiàn)的艱難歷程，也可以嘗試用前人的數(shù)學(xué)方法解決問題，從而培養(yǎng)創(chuàng)新意識(shí)和勇于探究的數(shù)學(xué)精神，增強(qiáng)對(duì)數(shù)學(xué)的好奇心，激發(fā)求知欲望.

案例1必修第一冊(cè)第52頁“探究與實(shí)踐”——利用等式證明不等式.

該閱讀材料首先給出了我國古代三國時(shí)期的數(shù)學(xué)家趙爽所繪制的弦圖，它利用圖形在割補(bǔ)后面積不變的原理，通過構(gòu)造幾何圖形（圖1）來證明勾股定理.由圖形不難得到關(guān)系式4×ab+（a－b）2=c2，即2ab+（a－b）2=c2，化簡(jiǎn)后也就是勾股定理.利用這個(gè)等式可以得到：a2+b2≥2ab，當(dāng)且僅當(dāng)a=b時(shí)等號(hào)成立.由此引發(fā)學(xué)生進(jìn)行探究：由等式證明一些不等式，如由等式證明三元平均不等式，由等式證明二元、三元、n元柯西不等式等.

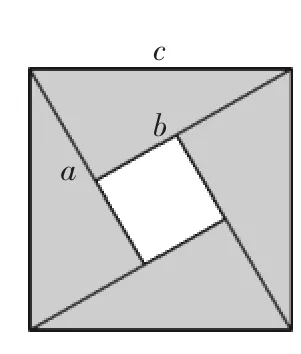
圖1

教學(xué)中，師生一起圍繞閱讀材料，重演前人對(duì)這些內(nèi)容的探索經(jīng)歷，嘗試用前人的方法解決一些數(shù)學(xué)問題，教師不僅要關(guān)注如何由閱讀材料經(jīng)過探究得到新的結(jié)論，更要重視借助閱讀材料滲透數(shù)學(xué)思想方法.本閱讀材料將數(shù)與形、代數(shù)與幾何結(jié)合起來，實(shí)現(xiàn)了數(shù)形的完美統(tǒng)一.

2.借助閱讀材料，強(qiáng)化數(shù)學(xué)應(yīng)用

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》指出教學(xué)中教師應(yīng)通過啟發(fā)，引導(dǎo)學(xué)生會(huì)用數(shù)學(xué)眼光觀察世界，會(huì)用數(shù)學(xué)思維思考世界，會(huì)用數(shù)學(xué)語言表達(dá)世界；強(qiáng)調(diào)數(shù)學(xué)與生活以及其他學(xué)科的聯(lián)系，提升學(xué)生應(yīng)用數(shù)學(xué)解決實(shí)際問題的能力.為培養(yǎng)學(xué)生應(yīng)用數(shù)學(xué)解決實(shí)際問題的能力，教材中閱讀材料的背景往往植根于日常生活，知識(shí)和生活緊密相連，讓學(xué)生體會(huì)到數(shù)學(xué)在日常生活中無處不在.

案例2必修第一冊(cè)第53頁“課后閱讀”——調(diào)和平均值與算術(shù)平均值不等式.

該閱讀材料描述道：在現(xiàn)實(shí)生活中，船速一定的汽船，在靜水中和有流速的河中往返航行同樣的距離，所需的時(shí)間是否一樣？有學(xué)生認(rèn)為二者所需的時(shí)間是一樣的，理由是：當(dāng)河水有流速時(shí)，汽船逆流上行雖然速度減慢，但回來時(shí)順流下行的速度會(huì)加快，二者互相補(bǔ)償，航行時(shí)間就應(yīng)同在靜水中往返一次所需的時(shí)間一樣.

上面的說法看起來有道理，但事實(shí)結(jié)果并非如此.設(shè)汽船在靜水中的航行速度為v靜，河水的速度為v水，汽船在河流中航行的單程距離為L(zhǎng)，則汽船逆流上行的實(shí)際速度是v上=v靜-v水，順流下行的實(shí)際速度是v下=v靜+v水，故汽船往返一次所需的時(shí)間是，這大于汽船在靜水中往返一次所需的時(shí)間，且河水流速越大，二者的差距越大.

學(xué)生利用已有知識(shí)解決問題的過程中，定會(huì)體會(huì)到獲得成功的喜悅感和學(xué)以致用的成就感，也會(huì)從中感悟到數(shù)學(xué)與現(xiàn)實(shí)世界的聯(lián)系.當(dāng)學(xué)生理解數(shù)學(xué)的同時(shí)，數(shù)學(xué)建模、數(shù)學(xué)運(yùn)算等核心素養(yǎng)也會(huì)提升.

3.借助閱讀材料，滲透人文素養(yǎng)

數(shù)學(xué)教育不僅傳授著數(shù)學(xué)知識(shí)，而且承載著育人功能.課本中，不少閱讀材料介紹數(shù)學(xué)史、數(shù)學(xué)家生平事跡、數(shù)學(xué)概念的來源等知識(shí)，對(duì)培養(yǎng)學(xué)生的人文素養(yǎng)有很大的幫助.因此，教學(xué)中應(yīng)指導(dǎo)學(xué)生學(xué)習(xí)這類閱讀材料，介紹中國傳統(tǒng)數(shù)學(xué)文化，加強(qiáng)中國數(shù)學(xué)文化的滲透，挖掘其中蘊(yùn)含的德育因素，以激發(fā)學(xué)生學(xué)習(xí)科學(xué)知識(shí)的動(dòng)力，達(dá)到“以文化人”的教育功能.

案例3必修第一冊(cè)第113頁“課后閱讀”——函數(shù)概念的形成和發(fā)展.

該閱讀材料介紹了函數(shù)概念的前世今生：函數(shù)概念起源于17世紀(jì)數(shù)學(xué)家關(guān)于運(yùn)動(dòng)的研究，通過日常生產(chǎn)、生活的實(shí)例發(fā)現(xiàn)，科學(xué)家研究運(yùn)動(dòng)需要探究?jī)蓚€(gè)變量之間的關(guān)系，正是因?yàn)檫@一實(shí)際需要，迫使人們開始研究?jī)蓚€(gè)變量，進(jìn)而逐步建立對(duì)函數(shù)的研究；后來對(duì)兩個(gè)變量的研究又拓展到數(shù)學(xué)領(lǐng)域，歐拉給出了函數(shù)的定義，到19世紀(jì)70年代，隨著集合論的出現(xiàn)，函數(shù)的概念也就更加清晰了，中文“函數(shù)”一詞是由我國清代數(shù)學(xué)家李善蘭從英文中翻譯過來的，這一名詞一直使用至今.

函數(shù)概念的演繹過程，體現(xiàn)了古代中外數(shù)學(xué)家不懈追求與探索的精神，創(chuàng)造了無數(shù)輝煌燦爛的成就.數(shù)學(xué)家的嚴(yán)謹(jǐn)踏實(shí)、追求真理的科學(xué)精神，會(huì)帶給學(xué)生極大啟示和教育，作為教師有責(zé)任有義務(wù)培育學(xué)生這種堅(jiān)韌不拔的數(shù)學(xué)精神，有助于他們?cè)谝院蟮纳詈蛯W(xué)習(xí)的道路上戰(zhàn)勝困難.

4.借助閱讀材料，創(chuàng)設(shè)問題情境

在教材中，對(duì)于不少數(shù)學(xué)內(nèi)容而言，如公式、概念、定理和結(jié)論等，缺少來源，缺少產(chǎn)生的背景.在課堂教學(xué)中，教師若只講解公式、概念、定理本身及其應(yīng)用，這樣的教學(xué)是乏味的，是殘缺不全的；完整的課堂教學(xué)活動(dòng)過程，應(yīng)當(dāng)涵蓋數(shù)學(xué)知識(shí)的產(chǎn)生背景、理論來源和應(yīng)用拓展這三方面的內(nèi)容.因此，教學(xué)中教師應(yīng)根據(jù)所授內(nèi)容的需要，創(chuàng)設(shè)合適的問題情境，以此來吸引學(xué)生的注意力，幫助學(xué)生感知和理解問題，提高課堂教學(xué)的有效性.比如，可以利用數(shù)學(xué)史創(chuàng)設(shè)問題情境，使得公式、概念、定理獲得“生長(zhǎng)點(diǎn)”“銜接點(diǎn)”.

案例4必修第二冊(cè)第126頁“課后閱讀”——話說向量.

教師上“向量的概念”一節(jié)課時(shí)，可以“話說向量”引入，多媒體展示“向量的故事”：早年的向量——物理學(xué)家稱之為矢量，只是物理學(xué)專門用來表示力和速度等物理量的工具，并不為數(shù)學(xué)家所重視.在歐幾里得集古希臘數(shù)學(xué)大成的《幾何原本》中，也沒有討論向量，即使到17、18世紀(jì)人們對(duì)向量的認(rèn)識(shí)也沒有什么根本性的變化.但進(jìn)入19世紀(jì)，事情有了重大變化，數(shù)學(xué)家們逐步認(rèn)識(shí)到復(fù)數(shù)可用來表示平面上的向量，平面向量與復(fù)數(shù)之間建立起了對(duì)應(yīng)關(guān)系.

在現(xiàn)代數(shù)學(xué)中，平面向量和空間向量被形式化地推廣為高維向量，形成了抽象的向量空間概念.向量連接著代數(shù)與幾何，連接著數(shù)學(xué)與物理.

通過以上向量產(chǎn)生及發(fā)展的過程，學(xué)生初步認(rèn)識(shí)到向量的由來及學(xué)習(xí)向量的重要性.筆者做過這樣一個(gè)訪談，用數(shù)學(xué)史創(chuàng)設(shè)問題情境，絕大多數(shù)學(xué)生認(rèn)為用數(shù)學(xué)史引入新課，感覺很有趣，學(xué)習(xí)數(shù)學(xué)也不枯燥了，還比較輕松.這次訪談?wù)f明學(xué)生學(xué)習(xí)數(shù)學(xué)知識(shí)的同時(shí)，想了解相關(guān)的數(shù)學(xué)史.正是學(xué)生喜歡這樣的數(shù)學(xué)課，使學(xué)生的學(xué)習(xí)由被動(dòng)變?yōu)橹鲃?dòng).

總之，新教材選用的這些內(nèi)容豐富，集應(yīng)用性、趣味性、人文性于一體的閱讀材料，與教材正文相互關(guān)聯(lián)、相互滲透，不僅使教學(xué)內(nèi)容豐富多彩，拓寬了學(xué)生的視野，深化了學(xué)生的知識(shí)，而且使學(xué)生學(xué)到了解決問題的方法，對(duì)培養(yǎng)學(xué)生的創(chuàng)新思維能力有著重要意義.所以，教學(xué)中教師應(yīng)走出認(rèn)識(shí)誤區(qū)，摒棄傳統(tǒng)應(yīng)試教育帶來的偏見，創(chuàng)設(shè)條件，激發(fā)學(xué)生的潛能，通過多種方法、多種手段挖掘這些材料豐富的人文和知識(shí)內(nèi)涵，實(shí)實(shí)在在做好閱讀材料教學(xué)，使之潛在功能得以真正體現(xiàn)，使得學(xué)科素養(yǎng)真正落地.