試題洞明皆學問“生”動溯源即文章
——2021年高考全國數學乙卷理科第12題解法探究及背景溯源
林鳳梅 福建省莆田第二中學 351131
蔡海濤 福建教育學院數學研修部 350025
高考試題是命題專家團隊的智慧結晶,具有規范性、權威性和科學性,認真研究高考試題的重要性不言而喻.每一道高考試題往往都是一個精彩的世界,它除了考查學生的知識、能力、思想、素養,具有較強的選拔功能外,還對中學教學起到了積極的導向和促進作用.通過研究近年的高考數學試題,細細地品味,不知不覺會感嘆高考試題演變的趨勢,會流連于試題所蘊含的深刻背景,會癡迷在各種精妙的解法里,真是越品越有味,題題都精彩.
筆者研究近年高考試題,發現比較大小的問題頻頻出現,無疑是高考命題的一個熱點考向,如2021年高考全國乙卷理科第12題、2021年高考全國乙卷文科第12題、2021年新高考Ⅰ卷第7 題、2020年高考全國Ⅰ卷理科第12題、2020年高考全國Ⅱ卷理科第11題、2020年高考全國Ⅱ卷文科第12題、2020年高考全國Ⅲ卷理科第12題、2020年高考全國Ⅲ卷文科第10題、2019年高考全國Ⅰ卷理(文)科第3題、2019年高考全國Ⅱ卷理科第6題、2019年高考全國Ⅲ卷理科第11題、2019年高考全國Ⅲ卷文科第12題等.這類試題主要考查冪函數、對數函數的性質等基礎知識,考查推理論證能力、運算求解能力和創新意識等,考查化歸與轉化思想、函數與方程思想、數形結合思想等,考查邏輯推理、數學運算等核心素養,體現綜合性和創新性.這類試題往往需要構造一個與待證不等式相關的函數,進而利用導數工具研究函數的單調性、最值來解決,學生解決該問題的難點主要在于如何構造函數.本文從一道2021年的高考題談起,研究這類問題的破解之道.
試題呈現
(2021 年高考全國乙卷理科第12題)設a=2ln1.01,b=ln1.02,c=則( )
A.a<b<c B.b<c<a
C.b<a<c D.c<a<b
分析:本題考查大小比較問題,這類問題利用近似估值計算往往無法解決,難度較大,難點是將各個式子的共同量用變量替換,構造函數,利用導數研究相應函數的單調性,進而比較大小.通過對數運算和對數函數單調性的研究不難對a,b的大小做出判定,由a=2ln1.01=ln1.012=ln(1+0.01)2=ln(1+2×0.01+0.012)>ln1.02=b,得b<a,接下來只需比較c與a,b的大小即可.
解法分析



評析:解法3類似于解法2的思路,構造函數f(x)=2ln(1+x),g(x)=ln(1+2x),h(x)=-1,比較三個函數導數值的大小得到f(x),g(x),h(x)的增長速度大小,可得c與a,b的大小關系.
背景溯源
本題的常規解法如上述三種解法,繼續探究會發現其背景深厚,內涵豐富,別具匠心.
背景1:貝努利不等式.
利用貝努利不等式(1+x)α≥1+αx(α≥2,x>-1),有(1+0.01)2>1+2×0.01=1.02,所以a>b.
背景2:泰勒展開式.
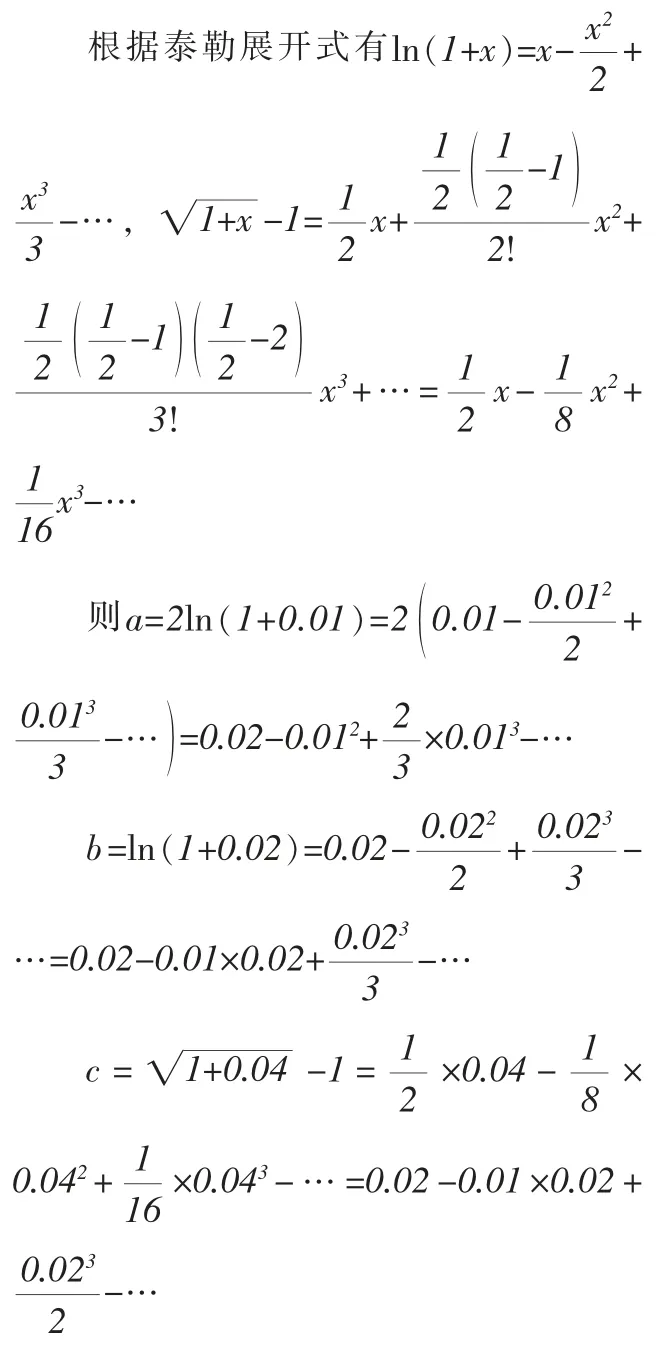
綜上,b<c<a.
背景3:常見不等式“ln(1+x)≤x(x≥0)”的加強.

解后反思
1.同構視角構造函數
同構式不等式是指除了變量不同,其余地方均相同的不等式[1].在大小比較問題中,如何構造函數是個難點,常用方法是先化同構式.如以上三種解法都是先比較幾個式子的結構特點,往往選擇一個較簡單或是與其他有關聯的式子,用變量x替換后,再把其他式子也用x表示出來,進而構造相應的函數.
同構變形常用的方法有:相同變量放一邊;運算形式變相同;指數、對數混合的一般統一化為以e為底的對數.
2.歸納方法領悟思想
本題解決難點是不能將不同形式表示的量轉化為同一類型的表達形式,恰當地構造函數,解題困惑的原因在于無法合理應用化歸與轉化思想及函數與方程思想.這啟發教師應將理性思維的培養貫穿教學過程,強調數學建模的過程教學,加強代數式合理變形的訓練,關注一題多解,加強思想方法的滲透.
3.聯想類比揭示本質
波利亞指出:“數學問題的解決僅僅只是一半,而更重要的是解題之后的回顧與反思.”不少學生解題后,校對好答案就“萬事大吉”,很少適度進行聯想,包括部分教師教學時往往也是就題論題,淺嘗輒止,缺乏對題目的深層挖掘.特別是高考這樣經典的試題,往往意蘊深遠,解題后嘗試多問“為什么”,適度進行聯想、類比、深化,將會透過表象發現問題的本質,長此以往積累解題經驗,以達到“做一題、通一類”的效果,從而提升學生的數學核心素養.

