星鏈衛星碰撞威脅及預警策略研究

張 煒， 張榮之， 王秀紅， 趙 治， 盧 欣

(西安衛星測控中心， 西安 710043)

1 引言

根據美Space-track 網站發布的數據，目前可被探測的空間目標數量已超過2 萬個，空間目標彼此間發生碰撞的幾率明顯增加。 實施軌道機動以規避高風險碰撞事件幾乎成為各航天大國為保證各自航天器和空間站安全需開展的常規動作[1]。 常用的碰撞預警方法有BOX 區域法[2]和碰撞概率法[3-4]。 早期美國航天飛機的碰撞預警采用BOX 區域法，以航天飛機為中心，若有空間目標進入其沿跡方向±5 km、徑向及法向±2 km范圍內時，航天飛機進行機動規避碰撞風險。 后逐步演化使用碰撞概率Pc作為判據，對于國際空間站(International Space Station， ISS)和航天飛機，設置了碰撞概率中風險閾值(Pc＝10-5)和高風險閾值(Pc＝10-4)，若Pc大于高風險閾值，就要進行規避控制，避免造成航天器硬件損傷[5]。

隨著巨型星座的逐漸部署，針對巨型星座開展空間安全分析已成為當前的研究熱點[6-9]。 星座大規模部署，將對空間碎片環境的可持續性產生重大影響。 一方面，衛星發射活動將增加空間碎片環境的密度，影響空間環境的穩定性；另一方面，星座衛星與其他在軌目標之間、星座衛星與星座衛星之間均存在碰撞風險，一旦發生空間碰撞事件極易產生凱斯勒效應，最終導致衛星無法長期安全運行。

星鏈(Starlink)計劃是SpaceX 公司推出的全球高速衛星互聯網計劃，旨在通過太空在全球范圍內提供互聯網接入服務，計劃部署4 萬余顆衛星，是迄今為止最龐大、最具代表性的巨型星座。本文從星鏈衛星的部署規律出發，分析了不同階段星鏈衛星對其他在軌衛星的碰撞威脅，針對其頻繁機動導致編目軌道預報誤差大等實際情況，分析了雙行根數(Two Line Element， TLE)的精度，驗證了碰撞概率判據的適用性，并提出了針對性的碰撞預警策略。

2 星鏈星座部署規律

2017 年3 月美國聯邦通信委員會(Federal Communications Commission，FCC)批準SpaceX 公司發射4425 顆星鏈衛星，2018 年11 月15 日又批準第二批共7518 顆衛星的發射計劃，星鏈星座規劃的衛星數達到了驚人的1 1943 顆。 為了減少如此數量龐大的衛星星座對近地空間造成的影響，2018 年12 月SpaceX 公司對星鏈計劃做出修訂，削減了第一批第一階段的衛星總數，由1600顆減少至1584 顆，軌道高度由1150 km 降至550 km，分布于24 個軌道面。 2019 年8 月，SpaceX公司再次對部署進行了修改，由24 個軌道面調整為72 個軌道面。

單顆星鏈衛星重約為260 kg，等效半徑為2.39 m[6]。 受限于火箭運載能力和發射成本，一般使用批量方式發射入軌，一批一般為60 顆，入軌高度較低，入軌后利用氪離子發動機進行軌道機動，逐步部署至工作軌道。 以第17 批星鏈衛星為例，基于Space-track 網站公開發布的TLE 根數[10]，入軌后，該批60 顆衛星的軌道高度變化情況如圖1 所示，其中每一條線表示一顆衛星的軌道高度變化，顏色相同的為同一組衛星，最終部署于同一個軌道面。

圖1 第17 批星鏈衛星軌道高度變化情況[10]Fig. 1 Orbital altitude of the 17th batch of Starlink satellites[10]

圖中可以看到，星鏈衛星發射入軌后主要有以下階段:

1)調整階段。 衛星發射入軌后進行軌道機動抬升至較低軌道(一般為350 km 或380 km)，進入調整階段，開展衛星狀態測試，并進行軌道面部署調整，也可稱為停泊階段。

衛星在調整階段停留的時間并不固定，短則幾天，長則數月，主要取決于星座構型需求。 同一批星鏈衛星的傾角相同，軌道面的差異主要來源于升交點赤經的漂移。 根據衛星軌道理論，升交點赤經的變化率可以表示為式(1)[11]:

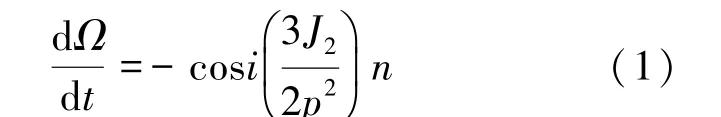
式中，Ω為升交點赤經，i為傾角，p為半通徑，J2為地球扁率特性的二次帶諧項，n為平均運動速度。 例如對于第17 批星鏈，其傾角為53 °，調整階段高度為380 km，升交點赤經的變化率約為4.89 °/d，550 km 工作軌道升交點赤經的變化率約為4.66 °/d，因此衛星經調整階段可形成的升交點赤經差Δφ可近似表示為式(2):

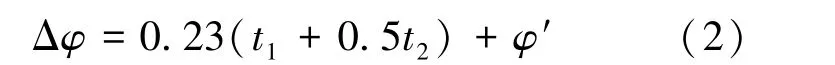
式中，t1為衛星在調整軌道停留的時間差，t2為從調整軌道機動至部署軌道的耗時，φ′為衛星機動過程對升交點赤經的修正量。

2)抬軌階段。 一般來說，同一批星鏈衛星入軌后采用分組的方式爬升至工作軌道，同一軌道面為一組。 同一批衛星從調整軌道爬升至工作軌道耗時基本相同，表明同一批衛星發動機參數及控制參數基本一致，例如第17 批星鏈衛星，耗時均為25 d 左右，每天抬升約6.8 km。 但是不同批次參數可能存在差異，例如第2 批星鏈，從調整軌道(高度為350 km)爬升至工作軌道耗時約33 d，每天抬升約6.0 km。

3)部署階段。 衛星通過軌道抬升到達預定工作軌道并實施部署，當前該高度主要為550 km和540 km，為維持部署高度，衛星需要進行常態化機動，以抵消大氣阻力的耗散作用。

此外還有降軌階段，SpaceX 公司對壽命末期的星鏈衛星實施主動降軌控制，以縮短衛星的在軌時間。 另有少部分星鏈衛星處于自然衰減狀態，在大氣阻力的作用下逐漸再入大氣層，這類衛星可當成普通無控空間目標處理。

3 碰撞威脅分析

利用TLE 數據對2 顆在軌衛星進行碰撞預警計算，所選取衛星的基本信息如表1 所示。 其中，40903 號衛星的平均軌道高度約為401 km，與星鏈衛星的調整階段高度、部署階段高度均無交叉，預警計算時段為2022 年2 月1 日至28 日；44777 號衛星的平均軌道高度約為538 km，與星鏈衛星部署階段高度存在交叉，預警計算時段為2021 年10 月1 日至31 日。 預警計算時段內未來3 d 接近距離小于5 km 的事件次數如圖2 所示，上圖為40903 號衛星每日預警的接近事件次數，下圖為44777 號衛星每日預警的接近事件次數，均區分了星鏈衛星和星鏈衛星以外的所有其他空間目標。

表1 兩顆在軌衛星的基本信息Table 1 Basic information of two test satellites

從圖2 可以看到，2 顆衛星所受的星鏈衛星碰撞威脅情況相差很大。 對于40903 號衛星，僅2 月23 日至25 日存在1 次與星鏈衛星的接近事件，其余時段均無近距離接近事件，該接近事件中的星鏈衛星為2021 年12 月18 日發射的第33 批星鏈衛星中的一顆，在抬軌過程中穿過40903 號衛星的運行區域造成碰撞風險。 44777 號衛星由于與星鏈衛星的部署高度存在交叉，全時均存在高頻次碰撞風險，所預警時段內，由星鏈衛星造成的接近事件次數日均約16.5 次，而其他空間目標造成的接近事件次數日均不到4 次，由星鏈衛星造成的碰撞威脅占約82%。

圖2 兩顆在軌衛星每日預警次數情況Fig.2 Closest events of two test satellites

綜合分析星鏈衛星的碰撞威脅結果，主要有以下3 類情況:

1)處于調整階段的星鏈衛星，高度一般為350 km 或380 km。 目前中國在此高度區域無衛星運行，星鏈衛星的影響基本可忽略；

2)抬軌/降軌階段的星鏈衛星。 星鏈從調整軌道抬升至部署軌道，或從部署軌道降軌再入大氣層，需穿過350～550 km 高度層，所有運行于該區域的衛星均可能受到影響。 但是由于星鏈衛星軌道高度抬升(或降低)速度在5 km/d 以上，威脅時間短，影響相對較小；

3)處于部署階段的星鏈衛星。 當前星鏈衛星的部署高度主要為550 km 和540 km，由于衛星部署密集，單一殼層衛星數量超過1500 顆，是對該區域其他衛星影響最大的一類。

無論哪類星鏈衛星，均采用小推力模式進行軌道機動，且不同階段衛星的控制策略差異較大，造成編目難度大。 由于無法獲知準確控制參數及后續軌控計劃，與其他無控類空間目標相比，星鏈衛星的軌道預報誤差更大，軌道結果用于測站跟蹤預報或碰撞預警計算的效果較差。 因此，需要針對星鏈衛星制定針對性的預警策略。

4 碰撞預警策略

4.1 星鏈衛星TLE 精度分析

4.1.1 方法

在無法獲取精密軌道的情況下，可使用內符合方法進行星鏈衛星TLE 精度分析。 假設存在2條TLE，歷元分別為t1和t2(t1＜t2)，選定第2 條TLE 為基準根數，并基于SGP4 模型生成某一時段內(一般是t1～t2之間)的位置速度作為基準軌道；利用第1 條TLE 生成相同時段的位置速度，并與基準軌道進行比較，即可得出該時段內第1條TLE 的精度情況。 內符合方法的關鍵在于找準基準軌道的時段，使得該時段的基準軌道與實際軌道最接近。 一般而言，TLE 前向預報和后向預報的精度是不同的，這主要取決于預報時段與擬合TLE 所使用軌道數據時段的重疊情況[12-13]。

以星鏈-2017(NORAD 編號為47351)為例，選取該目標2 條TLE，歷元分別為2021-02-23 19 ∶51 ∶31.98(UTC) 和2021-02-24 18 ∶52 ∶13.74(UTC)，間隔約為1 d，使用上述方法進行精度分析，結果如圖3 所示。 從圖3 可以看出，TLE1 的誤差主要在橫向(T方向)，隨時間逐漸減小，在TLE2 歷元時刻附近達到最小值，后又逐漸增大。此特性與其他空間目標有很大不同。 一般而言，空間目標TLE 由定軌段數據擬合，TLE 歷元為測量數據最后一點或最近升交點，因此前向預報與實際軌道較為接近。 而星鏈衛星大多處于頻繁軌控狀態，為了使預報段獲得更高的軌道精度，擬合TLE 時采用的是含軌控計劃的預報段數據。 針對星鏈衛星的這一特點，并結合誤差呈短周期變化的規律，對軌道生成策略進行適應性調整，選取的比較時段為(t2，t2＋Tsat) ，其中，Tsat為衛星軌道周期，分析該時段內TLE1 的誤差情況，作為TLE1 預報時長(t2-t1) 的誤差最大值。

圖3 內符合法TLE 精度示例(以星鏈-2017 為例)Fig.3 Accuracy for TLE using internal coincidence method(take Starlink-2017 as example)

4.1.2 數據

目前可公開獲取的星鏈衛星TLE 數據包括2類:①基于美SSN 監測網數據的編目結果，TLE的分類標識欄為U；②基于SpaceX 公司發布的含控制計劃的星歷數據擬合結果，TLE 的分類標識欄為C，本文記為TLE_C。 本文主要分析TLE_C數據的精度情況。

選取的2 個算例目標信息如表2 所示。 其中，星鏈-2305 發射于2021 年3 月24 日，2021 年10 月16 日至11 月18 日該衛星處于抬軌階段，平均抬升速度約為6.0 km/d；星鏈-1751 發射于2020 年9 月3 日，2021 年11 月10 日至12 月31日該衛星處于降軌階段，期間11 月26 日至12 月9 日無降軌動作，平均降低速度約為6.7 km/d。

表2 兩個算例目標的基本信息Table 2 Basic information of two test objects

4.1.3 結果

使用4.1.1 節所述方法分析2 個算例目標的軌道預報精度。 其中，表3、圖4 為星鏈-2305 TLE_C 數據預報1 d 和2 d 的誤差情況，表4、圖5 為星鏈-1751 TLE_C 數據預報1 d 和2 d 的誤差情況，σR、σT和σN分別為預報誤差在RTN坐標系中徑向、橫向和法向分量的標準差。此外，采用相同的方法分析了2021 年11 月3 日處于調整階段的93 顆星鏈衛星TLE_C 精度情況，結果如表5 所示。 部署階段星鏈衛星的精度情況與調整階段星鏈衛星相當，此處不在詳述。

表5 調整階段星鏈衛星TLE_C 的精度情況Table 5 The accuracy of Starlink satellites in adjustment stage using TLE_C

圖4 星鏈-2305 TLE_C 數據的精度情況Fig.4 The accuracy of Starlink-2305 using TLE_C

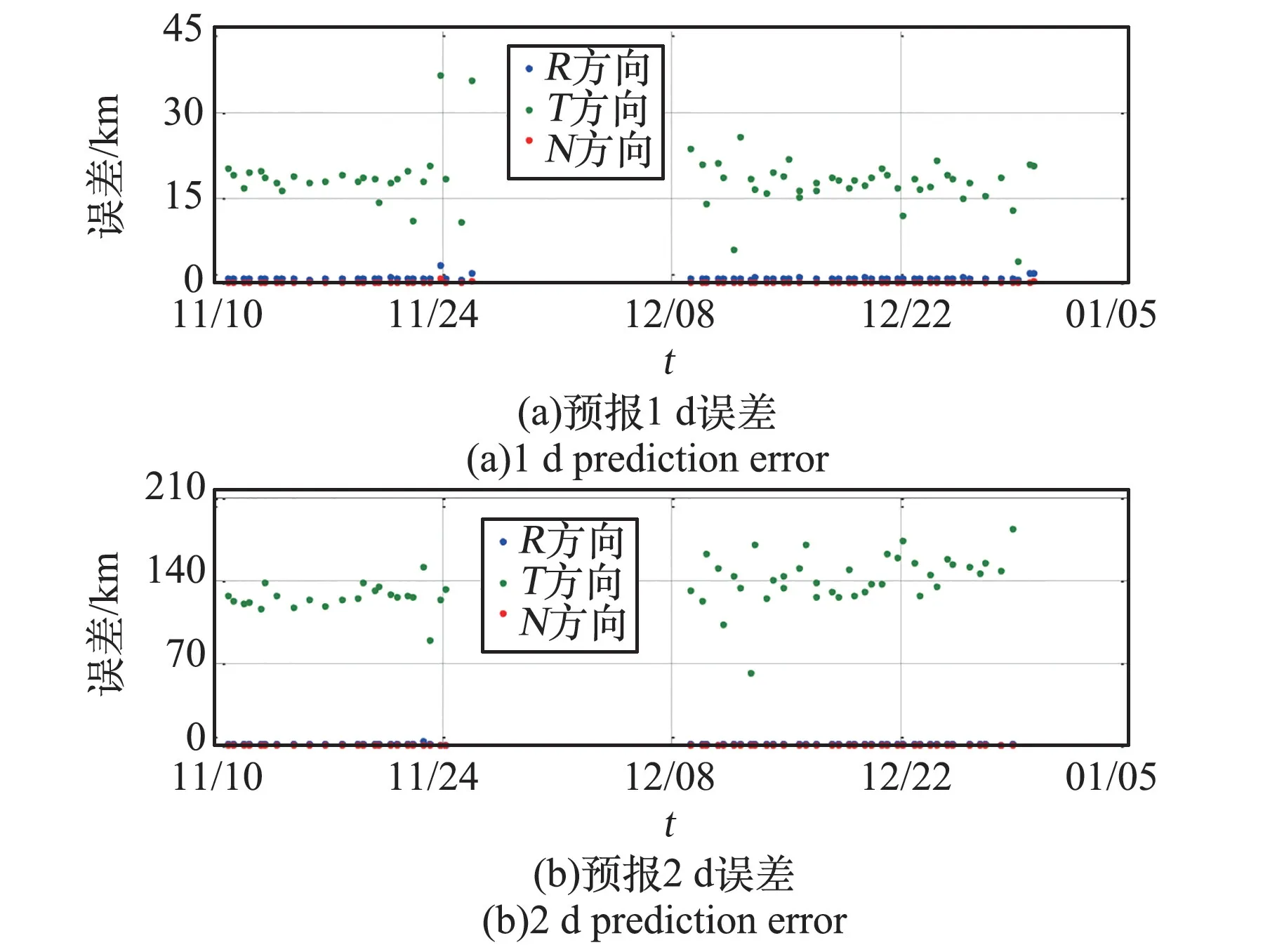
圖5 星鏈-1751 TLE_C 數據的精度情況Fig.5 The accuracy of Starlink-1751 using TLE_C

表3 星鏈-2305 TLE_C 數據的精度統計Table 3 The accuracy of Starlink-2305 using TLE_C

表4 星鏈-1751 TLE_C 數據的精度統計Table 4 The accuracy of Starlink-1751 using TLE_C

根據精度分析結果，可以得出以下結論:

1)TLE_C 的置信期較短，一般不超過24 h。例如調整階段的星鏈衛星24 h 預報誤差一般小于3 km，48 h 預報誤差接近40 km，原因可能是擬合TLE_C 時采用的是星歷數據的前部分數據，而非完整段；

2)不同階段星鏈衛星的預報精度不同。 一般來說，調整階段和部署階段星鏈衛星的TLE_C精度最高，預報24 h 位置誤差一般小于3 km，其次是抬軌階段的星鏈衛星，預報24 h 位置誤差一般小于8 km，降軌階段的星鏈衛星精度最差，預報24 h 位置誤差一般小于20 km。

另外需要說明的是，由于進行比較的2 條軌道均基于SGP4 模型計算，存在系統模型誤差[14]，因此實際誤差要大于本文分析結果。

4.2 碰撞概率判據的有效性分析

碰撞概率Pc是衛星碰撞預警工作中的一種常見判據。 碰撞概率值不僅取決于交會時刻衛星與空間目標的空間位置關系，還與2 個目標的尺寸、位置速度幾何關系、位置速度的不確定性等因素相關。Pc是兩目標中心的距離小于等效半徑之和的概率，可以表示為式(3):

式中，ρ表示兩目標中心的距離，R為兩目標的等效半徑之和。

碰撞概率的顯式表達式可以表示為式(4)[15]:

假設Δh、Δl均為0(即2 個目標的接近距離為0)，在軌衛星的等效半徑為5 m，星鏈衛星的等效半徑為2.4 m，為1000 m，為300 m，Pc隨星鏈衛星T方向分量誤差的變化如圖6 所示。從圖6 可以看出，隨著T方向誤差增大，碰撞概率減小，且軌道面夾角越小，變化越明顯。 若軌道面夾角φ為20 °，T方向誤差為5 km 時，碰撞概率約為5.5E-6；T方向誤差為10 km 時，碰撞概率約為2.8E-6。 若軌道面夾角為φ為150 °，T方向誤差為5 km 時，碰撞概率約為2.1E-5；T方向誤差為10 km 時，碰撞概率約為1.0E-5。 另外，圖6 示例中假設2 個目標的接近距離為0，實際計算時幾乎不可能出現，而Pc隨Δh、Δl的增大而減小，因此實際計算出的碰撞概率更小。

圖6 碰撞概率隨T 方向誤差變化Fig.6 Changes of collision probability with the error in T direction

以4.1 節中的2 個算例目標為例，利用公開的TLE 數據計算與48274 號航天器的接近情況，計算碰撞概率時48274 號航天器的等效半徑取為20 m，結果如表6 所示。 最終得到星鏈-2305 衛星與該航天器的碰撞概率為9.8E-7，星鏈-1751 衛星與該航天器的碰撞概率為3.5E-6，均小于1E-5。

表6 2 顆星鏈衛星與48274 號航天器的接近情況Table 6 The collision information between two Starlink satellites and Satellite No. 48274

若軌道誤差過大，空間目標位置定位的不確定性增大，碰撞概率衰減至一個很小的值，但是并不意味著碰撞風險減小，最終導致碰撞概率置信度降低[16]。 在與星鏈的碰撞問題中，碰撞概率判據是否有效主要取決于軌道數據的精度情況。 抬軌階段星鏈衛星TLE 數據T方向24 h 預報誤差一般大于8 km，降軌階段的誤差更大，基于TLE進行碰撞預警計算幾乎不可能出現高風險接近事件(碰撞概率值大于1E-4)，因此認為碰撞概率不適合作為2 個階段星鏈衛星的預警判據；而調整階段和部署階段星鏈衛星的TLE 數據精度較高，碰撞概率值仍具有較高的置信度。

4.3 針對星鏈衛星的碰撞預警策略

根據第2 節星鏈衛星部署規律、4.1 節TLE數據精度情況及4.2 節碰撞概率判據適用性的分析結果，針對星鏈衛星的碰撞預警策略建議如下:

1)由于星鏈衛星TLE 的置信期較短，需要對星鏈衛星的預警時長進行調整，一般預警時長不超過24 h；

2)不同階段星鏈衛星的軌道數據精度不同，需采用不同的判據。 對于調整階段和部署階段的星鏈衛星，由于TLE 數據的精度較高，可采用碰撞概率或碰撞概率與BOX 區域相結合的判據；對于抬軌或降軌階段的星鏈衛星，在當前精度條件下幾乎不可能出現碰撞概率大于1E-4 的高風險接近事件，與碰撞威脅客觀存在的實際不符，因此建議采用BOX 區域作為預警判據；

3)采用BOX 區域作為判據時，需要根據不同階段星鏈衛星的軌道精度情況分別確定各方向的距離閾值；

4)星鏈衛星的軌控計劃與實際軌控的實施可能存在差異，導致少數TLE 的誤差較大，可通過增加預警頻次來降低影響。

5 結論

1)在軌衛星受星鏈衛星的碰撞威脅情況與衛星運行區域有關。 若衛星運行于350 ～550 km高度之間，接近事件與星鏈衛星的抬軌時機有關，影響較小；若衛星運行于星鏈衛星的部署高度，星鏈衛星的影響很大，部分衛星80%以上的碰撞威脅均來自于星鏈衛星；

2)對處于持續抬軌和降軌階段的星鏈衛星，由于軌道預報誤差大，碰撞概率的置信度降低，不適合作為該階段星鏈衛星的預警判據；而調整階段和部署階段星鏈衛星的軌道預報精度較高，碰撞概率值仍具有較高的置信度。