基于GS-SVR模型的空腔積水水深和長度預測

郭港歸，李國棟，魏 杰，王立杰

(1.西安理工大學西北旱區生態水利國家重點實驗室,陜西 西安 710048；2.中國電建集團中南勘測設計研究院有限公司，湖南 長沙 410014)

水流摻氣[1-2]是防止高水頭泄水建筑物空化空蝕的主要措施。然而，小底坡下的摻氣坎常出現空腔回水現象，導致空腔形態較差，嚴重時甚至被積水填滿，導致摻氣量不足，難以達到摻氣減蝕的效果。空腔積水水深和空腔長度是衡量摻氣設施效率的重要指標[3]，因此研究坎下水力特性與空腔積水水深、空腔長度的關系具有重要的工程價值。前人對空腔積水水深和空腔長度進行了較多的理論公式推導：楊永森等[4]運用動量方程對控制水體進行受力分析，計算出空腔積水深度；徐一民等[5-6]以微元法為基礎，建立空腔回水方程計算空腔積水水深和空腔長度，計算值與試驗值趨勢一致；Chanson[7]利用拋射體公式計算射流空腔長度和回水長度，與實測值相比計算結果偏大；潘水波[8]對拋射體公式引入3個修正系數，計算精度相對提升。

目前機器學習的方法已廣泛應用于局部沖刷、水質預測和流量系數預測等水科學領域，人工神經網(artificial neural network，ANN)和支持向量機(support vector machine，SVM)是其中重要的方法。由于ANN需要設置復雜的網絡結構參數，導致模型收斂緩慢，甚至在小樣本數據下容易造成過擬合[9]，降低預測準確度。SVM以最小結構化風險原則代替傳統經驗風險方法[10]，在處理小樣本數據中有著天然的優勢，泛化能力強，有效防止過擬合，其拓撲結構主要由自身的超參數決定，通過對超參數(C和γ)進行優化使模型達到較高的預測精度。Zaji等[11]用適湊法確定了SVM模型的超參數并對三角形側堰的流量系數進行預測；Jain[12]通過現場實測數據建立SVM模型模擬河道水位、流量和含沙量的關系；Kiyoumars等[13]采用粒子群算法(PSO)優化SVM模型實現對階梯溢洪道流量系數和消能率的預測；趙慶志等[14]通過網格搜索的方法對超參數進行尋優，得到了基于LS-SVM的短期降雨預測模型。

本文通過網格搜索和交叉驗證的方法建立SVM回歸(GS-SVR)模型，研究超參數C和γ之間的規律和其對模型性能的影響。基于GS-SVR模型，依據評估指標判別6種參數輸入中的最優組合，實現了對空腔積水深度和空腔長度的準確預測，并采用敏感性分析尋找對該模型起關鍵作用的因素。

1 試驗數據

本文基于沈春穎[15]的試驗數據集，建立GS-SVR模型。試驗水槽全長7.6 m，槽寬10 cm，來流量的范圍為0～5.5 L/s，挑坎體形如圖1所示。在不同的挑坎體形和來流條件下進行模型試驗，分別測量水深h、挑坎坡度i1、挑坎高度Δ、空腔積水水深h1、空腔長度L、水舌沖擊角θ和底坡坡度i2。試驗數據總量162組，范圍見表1。

表1 試驗數據范圍

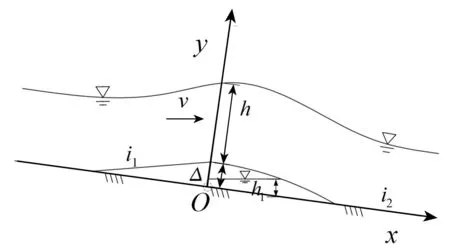
圖1 摻氣坎布置方式

采用皮爾遜相關系數r反映各變量之間的相關性，皮爾遜相關系數如圖2所示，圖中v為坎頂流速。試驗輸出變量包括h1和L，其余除θ以外均為輸入變量。當2個變量之間的皮爾遜相關系數|r|>0.3，則認為兩變量之間相關性較強，輸入變量應避免兩兩之間有較強的相關性，確保變量的相對獨立性。由圖2可知，輸入變量之間的相關系數的絕對值多數小于0.3，表明各輸入變量獨立性較好。輸出變量h1與Δ、θ和i2的相關性較強，相關系數分別為0.73、0.5、-0.43，當Δ和θ增大時，均導致h1增加，而隨著i2增大，h1減少；輸出變量L受到Δ和v的影響較大，相關系數分別為0.61和0.57，說明v和Δ增加時，L隨之增加。

圖2 變量相關性分布

2 GS-SVR模型的建立

先利用量綱分析法確定需要的輸入變量，在此基礎上選擇不同的輸入組合，并對其進行歸一化處理。采用網格搜索和交叉驗證的方法優化不同訓練樣本比例和輸入組合的SVM模型，建立最佳輸入組合下的GS-SVR模型，并分析模型超參數C和γ的分布規律。

2.1 量綱分析與變量組合

采用表1中的物理模型試驗數據建立SVM模型，預測小底坡低弗勞德數泄洪洞的h1、L。h1和L是衡量摻氣設施是否符合要求的重要指標。根據文獻[16]可知h1和L均受到以下因素的影響：

Y=f(i1,i2,h,v,Δ,Δp)

(1)

式中：Y為h1或L；Δp為空腔內外壓力差。摻氣設施通氣充分時，Δp對空腔長度和空腔積水水深的影響可以忽略不計。基于量綱分析方法[17]，可由式(1)得到：

(2)

由于Δ與h具有相同量綱，因此等效后得到另一種形式：

(3)

變量組合見表2和表3，WD1～WD4與CL1～CL4以式(2)為基礎的輸入組合，輸入變量依次降低，探究變量數目對模型的影響；WD5～WD6與CL5～CL6以式(3)為基礎的的輸入組合，對比不同量綱化方式對模型性能的影響。

表2 空腔積水水深模型的變量組合

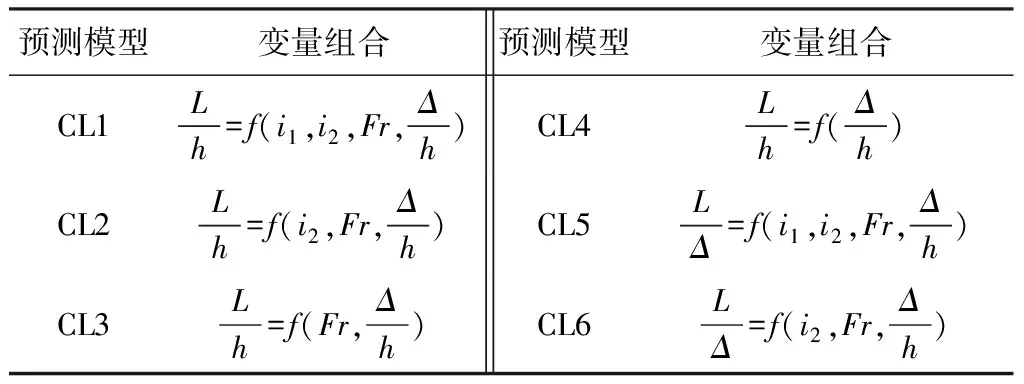
表3 空腔長度模型的變量組合

2.2 數據預處理

2.2.1歸一化處理

原始數據中，各變量之間的數值差異較大，影響模型的預測性能，因此對數據進行預處理是必要的。在無量綱化后，采用式(4)進行歸一化，統一變量范圍到0～1之間。

(4)

式中：xmin為樣本數據的最小值；xmax為樣本數據的最大值；x*為歸一化后的值。

2.2.2訓練集、測試集和交叉驗證

許多研究者只將數據集分為訓練集和測試集，模型從訓練集中學習，在測試集中調整SVR模型超參數。而實際中很多時候缺少未來的數據，并且由于測試集用于模型調參，導致測試數據的信息提前泄漏到模型中，造成模型預測結果精度偏高、不能反映模型的泛化性能，容易產生過擬合[18]。為了解決上述問題，需要提取一部分數據作為驗證集，模型在訓練集上學習，在驗證集上調參，測試集用于最終評估。然而，數據集分為3組將大大減少可用于模型學習的樣本數量，造成模型訓練不充分，導致計算結果存在隨機性，而k折交叉驗證(k-CV)的方法能有效解決樣本容量小的問題。k-CV將原訓練集拆分為k個較小的集合，對于每一個小集合都遵循以下原則：①使用k-1折數據作為模型的訓練數據；②模型對剩下1折數據進行驗證；③k-CV的模型評估指標是k次循環中的平均值(該指標可用于模型泛化水平的度量)。交叉驗證的方法不會浪費數據，非常適合數據樣本總量較少的情況。本試驗將采用五折交叉驗證的方法，具體步驟如圖3所示。

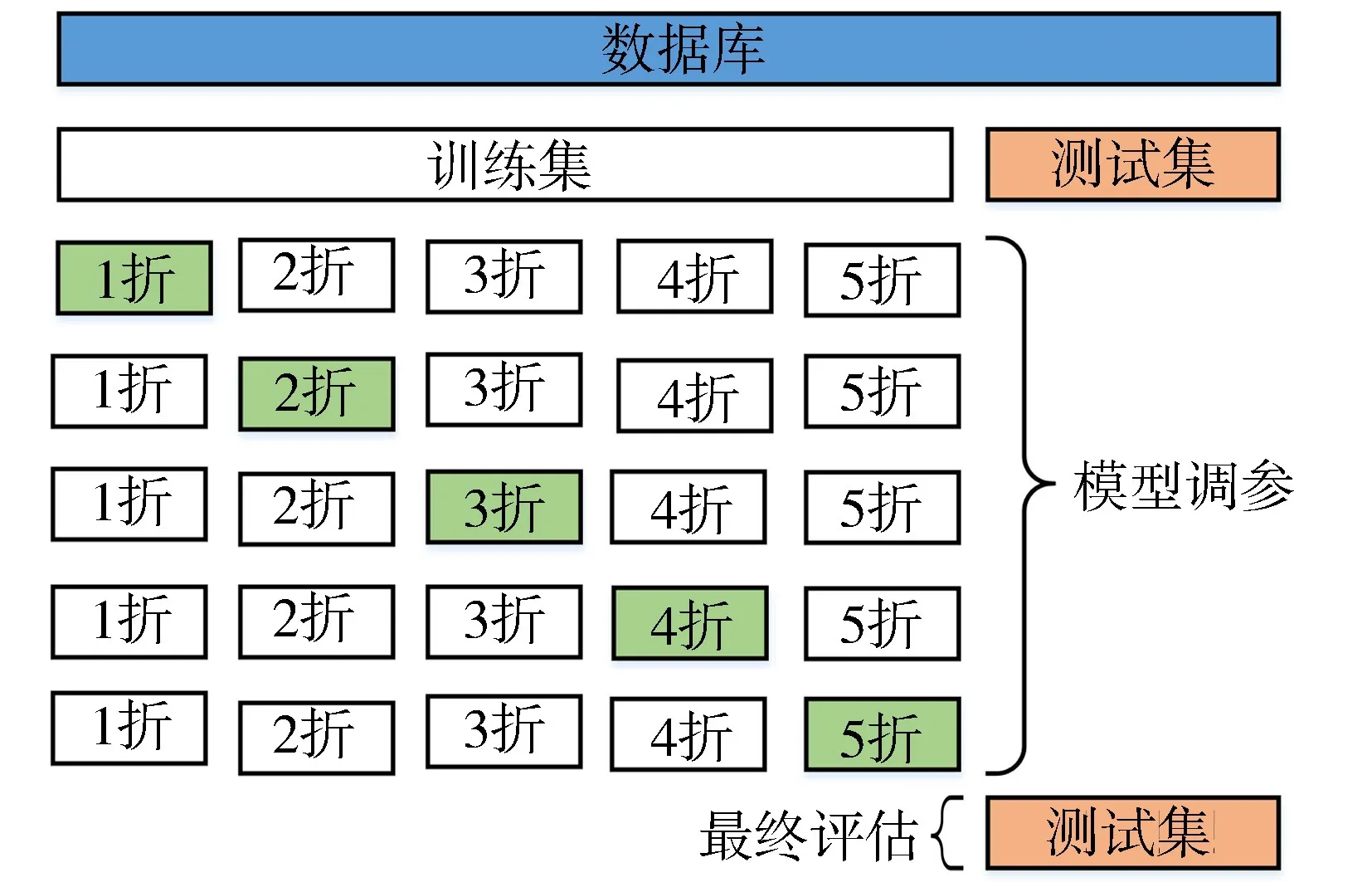
圖3 五折交叉驗證示意圖

2.2.3訓練樣本抽取比例

訓練樣本數量占總樣本數量的比重會影響SVR模型的性能。本試驗選取訓練樣本抽取比例分別為50%、60%、70%和80%，采用網格搜索和交叉驗證的方法預測空腔積水水深h1和空腔長度L。模型指標選取相關系數R2，不同抽取比例下的分布如圖4所示。由圖4可知，隨著訓練樣本量增加，訓練集、交叉驗證集(CV)和測試集的模型指標R2均增加。說明該模型性能隨著訓練數據的增加而提高。因此，本次試驗選擇訓練集占總樣本集的80%為基準比例。

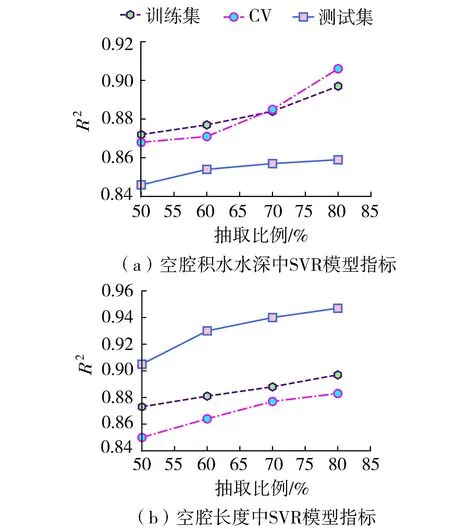
圖4 SVR模型指標分布

2.3 網格搜索法優化GS-SVR模型超參數

GS-SVR模型具有良好的泛化性能，而其模型性能依賴于它的超參數[19]。SVR的超參數主要包括正則化系數C和核參數γ。C代表模型復雜度[20-21]，C取值較大時，模型會盡可能擬合所有訓練數據，可能造成模型過擬合。核參數γ是核函數的內置參數，代表影響支持向量的強度[20]。

網格搜索[22]是最常見的尋優算法之一，其主要目的是讓尋優超參數C和γ在一定坐標范圍內、根據規定步長劃分網格，并遍歷所有的網格，對選定的網格節點的所有超參數組合C和γ利用k折交叉驗證得到模型交叉驗證評估指標(R2)，最終取使模型交叉驗證評估指標R2最高的那組C、γ為最佳超參數組合。

圖5為基于網格搜索下的h1和L預測模型的超參數分布，其中C和γ均在2-8～28之間，分別在各范圍內取100個網格點(總網格數100×100=10 000)，根據圖上的等高線和顏色分布可以找到交叉驗證評估指標R2取值較大時的位置。試驗結果表明，在所有的輸出組合和訓練抽取比例下，交叉驗證評估指標均呈現相似的分布，因此僅展示3張圖(圖5)。圖5中C和γ對模型性能影響較大。中間黃色區域的R2>0.7，模型性能較好；左上和左下深藍色區域C取值較小，造成模型欠擬合；圖右上淺藍色區域γ較大導致模型過擬合，模型性能不理想。深黃色區域中模型性能進一步提高(交叉驗證評估指標R2>0.86)，沿著該區域能夠找到交叉驗證評估指標R2取值最大的點，該點對應最優超參數組合。深黃色區域中，當C增至+∞時，則γ趨于-∞，說明超參數處于相反的增長趨勢。C增大實現模型對樣本充分訓練，同時減少γ防止其過度訓練，最終模型的預測結果處于最佳狀態，因此SVR保持其良好泛化性能和高預測精度的機制是通過平衡C和γ的大小來實現的。

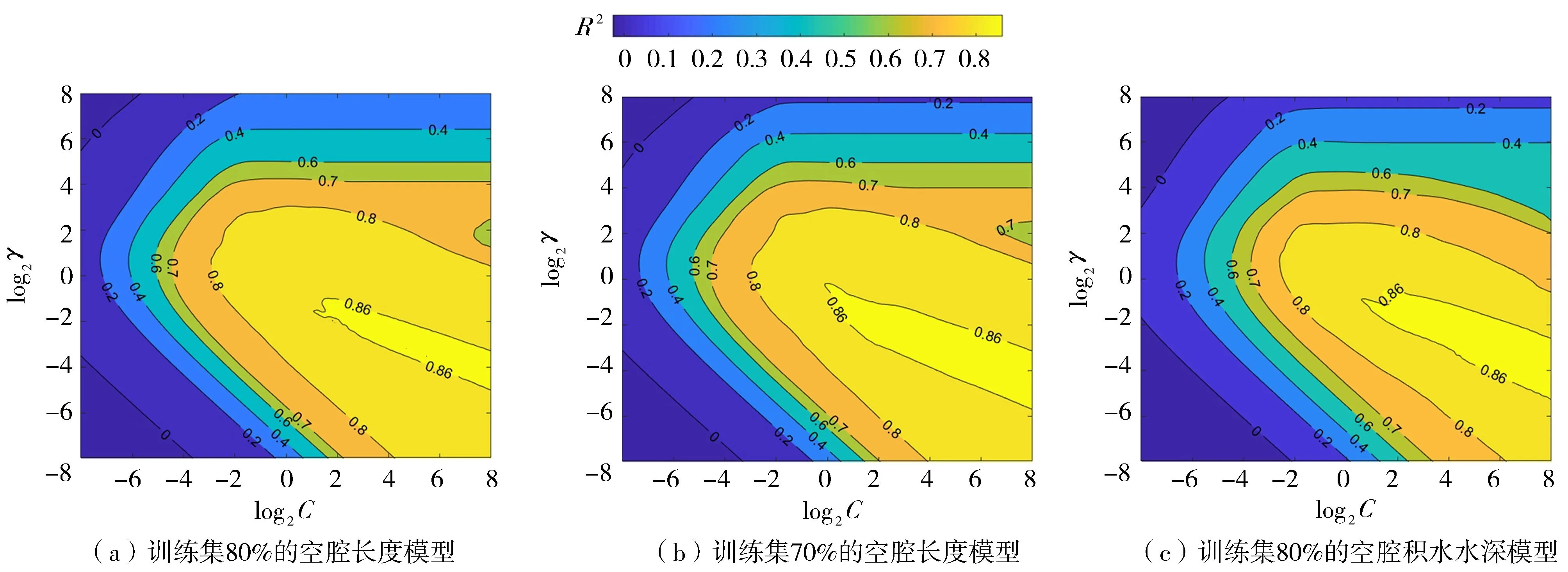
圖5 網格搜索中R2的分布情況

3 GS-SVR模型計算結果與分析

3.1 模型計算結果

空腔回水和空腔長度是小底坡、低弗勞德數泄洪洞摻氣設施設計中關注的指標，通過GS-SVR分別對6種參數不同輸入組合進行分析，模型評估指標選取R2和均方根誤差RMSE。

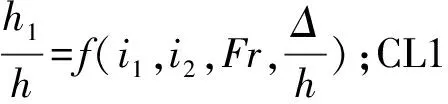
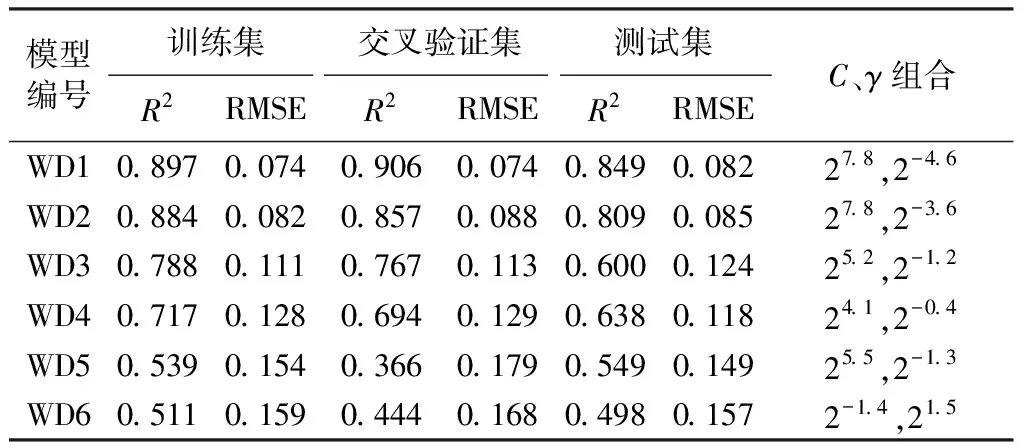
表4 空腔積水水深的模型指標

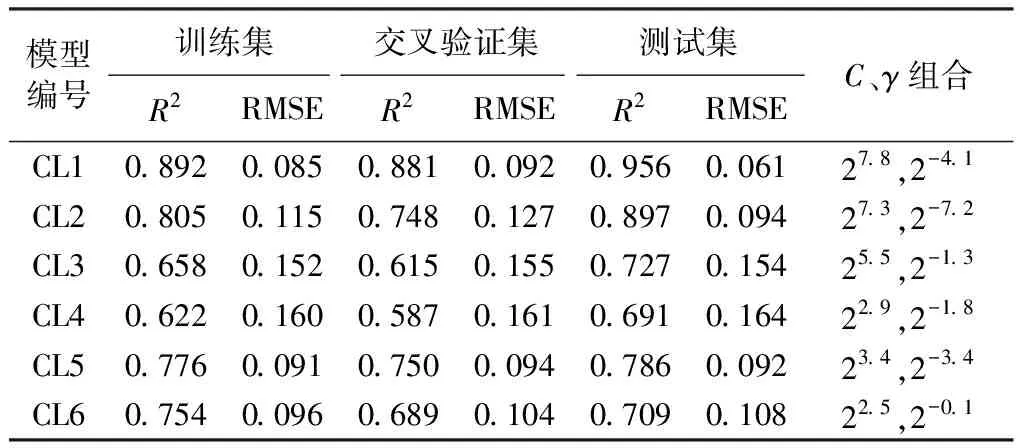
表5 空腔長度的模型指標

3.2 模型敏感性分析

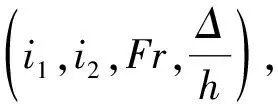
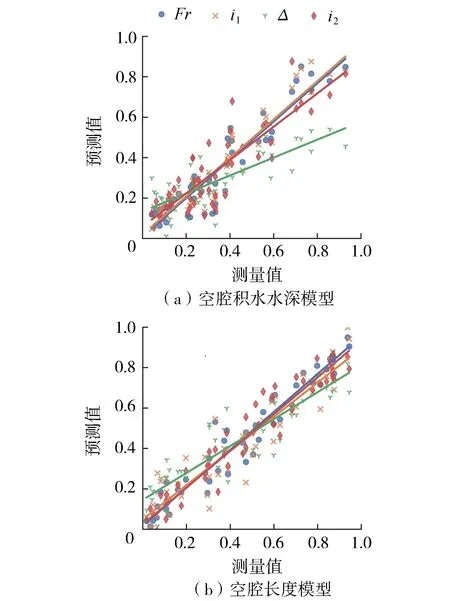
圖6 敏感性分析

結合變量相關性分析發現，相關性分析與敏感性分析聯系緊密，相關系數大的輸入變量對模型影響大。因此，在建模之前可以通過相關性分析選擇重要的輸入變量。

4 結 論

a.原數據中，各輸入變量之間獨立性較好；輸出變量空腔積水水深和空腔長度均與輸入變量存在相關性。根據不同抽取比例訓練集的結果發現，小樣本容量中，較大的訓練集抽取比例能提高GS-SVR模型的性能。

b.通過網格搜索和交叉驗證的方法對模型超參數進行優化，發現該方法能找到最佳超參數組合、提高模型性能，并且GS-SVR模型計算結果的高準確度機制是通過超參數C和γ的相互制約來實現。

c.6種不同輸入組合的計算結果表明，保持GS-SVR模型復雜度和樣本復雜度一致并且采用合適的量綱化方式會極大改善模型性能，在此基礎上尋找最佳變量組合，實現對空腔積水水深、空腔長度的精準預測。

d.敏感性分析發現，空腔積水水深模型對坎高和坎下底坡較為敏感，空腔長度模型僅對坎高敏感。本文試驗由于弗勞德數變幅較小，而SVM預測結果依賴于試驗數據，故建模型的通用性有待考量，未來可收集更多摻氣坎體型下的試驗數據，擴大模型應用范圍。