助飛魚雷模態振型斜率仿真計算

王升,白治寧,郭君

(中國船舶集團有限公司 第705 研究所,陜西 西安,710077)

0 引言

導彈若未考慮彈體的彈性振動可能導致發射飛行失敗,因此,新研制的導彈和運載火箭都會通過振動特性試驗測量其結構動力學特性,其中主要的參數就是振型斜率[1-2]。助飛魚雷與導彈、運載火箭的結構特點相似,其長細比較大,結構剛度較小,在氣動力的作用下也會產生變形和彈性振動,將影響敏感元件慣性測量組合的測量精度,甚至會錯誤地判斷全雷的飛行姿態。在研究和設計助飛魚雷的姿態控制系統時,同樣必須考慮全雷的彈性變形影響,通過全雷振動特性試驗,獲得準確的模態參數以及慣組安裝位置的振型斜率作為姿態控制設計輸入參數[3],以確保飛行過程姿態能夠得到穩定控制。

全雷振動特性參數往往在產品加工后通過振動特性試驗獲得,在產品研制階段,慣組安裝位置確定和姿態控制設計所需要的模態參數以及慣組安裝位置的振型斜率,只能通過仿真分析方法獲得。且在新的產品研制模式要求下,通過仿真方法獲得準確的振動特性參數尤為重要。目前模態振型斜率的仿真分析在導彈和火箭領域均有研究成果:潘忠文[4]在傳統等效梁模型基礎上,對局部結構詳細建模方法進行了全箭動特性分析及振型斜率的仿真分析;李家文等[5]通過對比2 種振動建模方法,建立了捆綁火箭姿態動力學新模型;祁峰等[6]通過艙段試驗完成了精細化建模及修正,進行了全箭模態振型斜率的仿真分析;蘆旭等[7]在研究了局部三維有限元精細模型建模方法,并分析了局部連接剛度對振型斜率的影響。

助飛魚雷因其獨特的楔環和分離艙連接結構等特點,與導彈及運載火箭具有明顯的區別。文中基于模態分析進行了助飛魚雷振型斜率的仿真計算,建立了助飛魚雷全雷三維詳細動力學模型,進行全雷模態分析,并計算了慣組安裝位置處的振型斜率,比較了發動機滿載和空載時的差異。

1 彈性體振型斜率計算原理

對于多自由度一般粘性阻尼結構系統[8],當外部激勵為零時,其動力學微分方程為

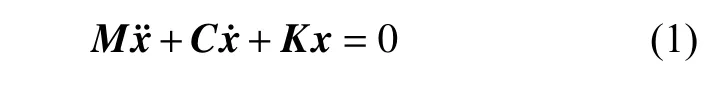
式中:M為質量矩陣;x為位移列陣;C為阻尼矩陣;K為剛度矩陣。

求解上述方程都轉化為求解式(2)的廣義特征問題,即

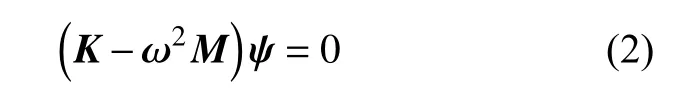
式中:ω為特征值,即彈性體的模態頻率;ψ為特征向量,即彈性體的振型。

分析彈性體振動特性時,結構力學中一般基于質量歸一化進行計算。但計算姿態控制系統設計所需的振型及振型斜率時,需要按某一參考節點進行歸一化處理,假設參考點振型向量中振幅為uj,則相應階次的振型向量為

2 動力學建模

將助飛魚雷全雷模型進行簡化處理,保留殼體及主要連接結構,如魚雷中的楔環連接結構、分離艙與魚雷的止推塊結構、分離艙和儀器艙的卡箍結構等,將部分內部安裝的零部件簡化為質量點。簡化后的助飛魚雷計算模型如圖1 所示,圖中點A～I為設置的質量點。

圖1 助飛魚雷全雷簡化模型Fig.1 Simplified model of a rocket-assisted torpedo

將簡化后的模型導入Hypermesh 軟件中進行網格劃分,大部分采用6 面體單元,小部分采用4 面體單元,模型網格單元總計146 萬余個,網格質量良好。網格模型如圖2 所示。建立計算模型過程中,盡可能使主要連接結構與實際產品相同,如分離艙與魚雷的止推塊和止推槽模型、分離艙與設備艙的卡箍結構模型、楔環連接結構的陰陽頭和楔環帶模型等。上述3 種連接模型如圖3所示。

圖2 有限元網格模型Fig.2 Models of finite element mesh

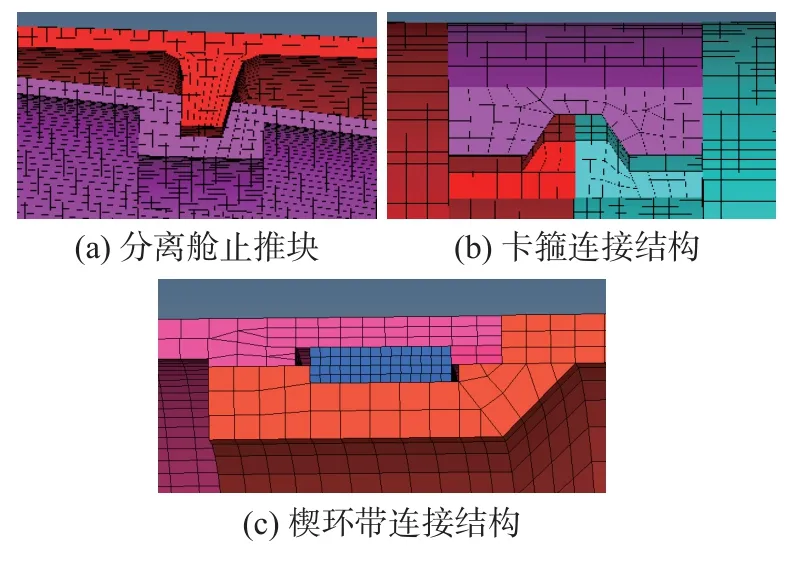
圖3 典型連接結構模型Fig.3 Typical connection structure models

為保證計算模型的準確性,計算模型的質量質心與實際模型相差不大,如表1 所示,其中質心位置為距雷頭的軸向距離。

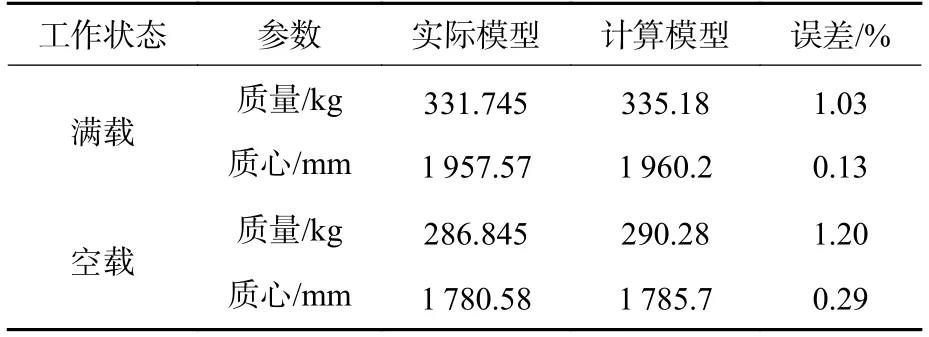
表1 計算模型物理參數Table 1 Physical parameters of calculating model

在Workbench 軟件中進行助飛魚雷的模態計算。計算模型的前處理過程中將大部分零部件間的接觸設置為綁定狀態,根據以往經驗,考慮到魚雷楔環連接結構的連接剛度較小,對全雷模態影響較大,其接觸法向罰剛度系數取值0.00008,使楔環連接結構的連接剛度接近真實情況[9],保證彈性振動參數分析結果更加準確。因助飛魚雷近似為回轉體結構,認為其俯仰和橫向振動特性相同,因而只分析計算助飛魚雷的橫向振動參數。

計算助飛火箭發動機滿載(0 s)和空載(10 s)工況的模態,以模擬飛行過程中的2 個工作狀態。

3 振動參數計算

3.1 模態振型

模態計算中,提取助飛魚雷全雷前3 階橫向彎曲模態。全雷模態計算結果如表2 所示。從表中可以看出,各狀態全雷同一階模態振型相似,其中滿載狀態的全雷前3 階模態振型如圖4所示。

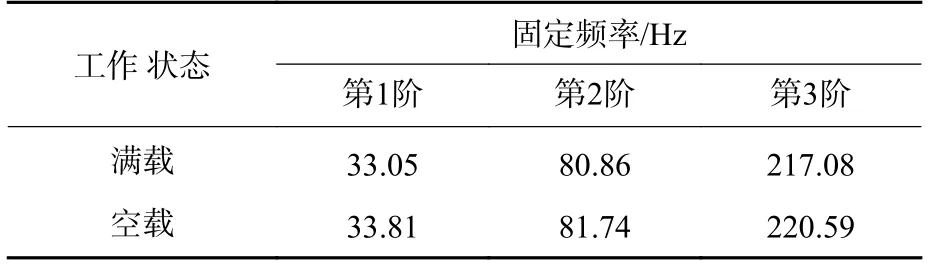
表2 全雷前3 階模態振型Table 2 The first three order modal shapes of the whole torpedo

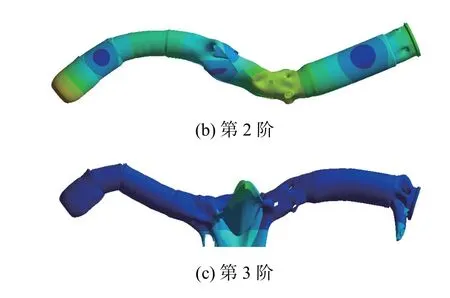
圖4 滿載狀態下全雷前3 階模態振型Fig.4 The first three order modal shapes of the whole torpedo at full load state

3.2 全雷振型函數

彈性體的橫向振動可看作一系列分量的疊加,即

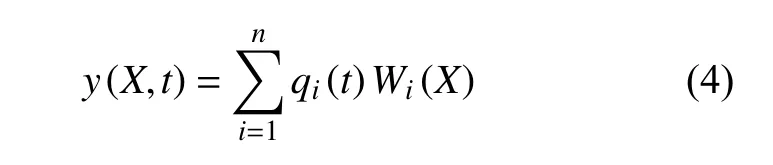
式中:y(X,t)為 振動位移;Wi(X)為彈性體第i階固有振型函數;qi(t)為第i階振型振動的廣義坐標。

在進行彈性體振動特性參數計算時,通常取前3 階模態進行分析計算。分析過程中將連續體離散處理,計算助飛魚雷分析節點的振型向量。分析節點的數量(體現為間隔疏密)會影響斜率值的精確度,認為節點的數量應為能夠反映關心模態振型的最小節點數的3 倍以上為佳,文中分析助飛魚雷前3 節模態,至少需要5 個節點,那么計算振型斜率則至少需要15 個節點,因而文中分析模態振型斜率時在助飛火箭全雷二象限母線上取20 個等分節點,并在慣組安裝處取1 個節點,21 個分析節點位置如表3 所示。

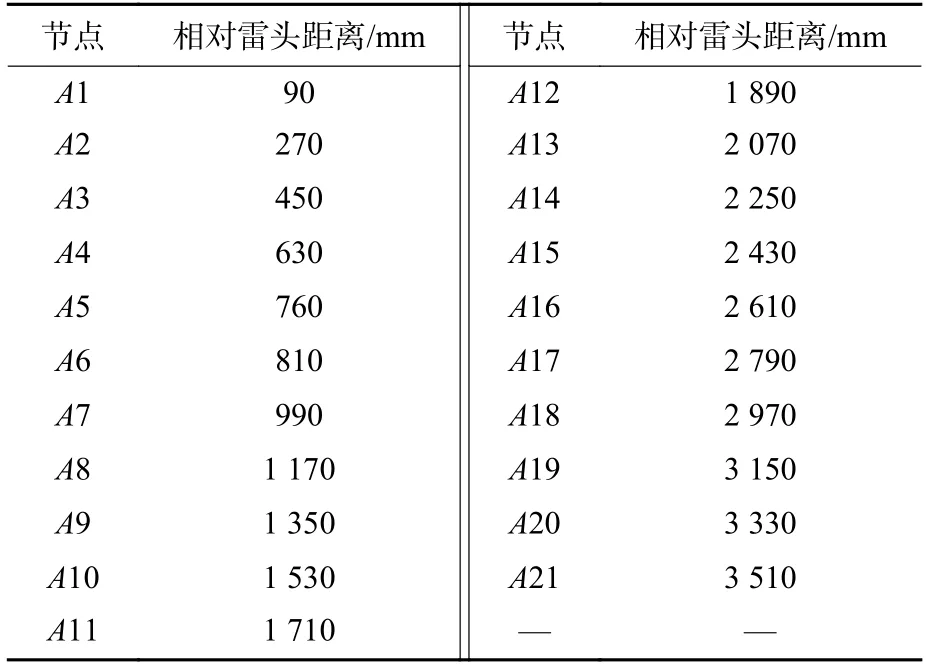
表3 分析節點位置Table 3 Position of analyzed nodes

通過后處理計算得到該21 個節點的振型向量,各計算狀態分析節點的各階振型如表4 所示。

表4 全雷分析節點模態振型Table 4 Modal shapes of torpedo’s analyzed nodes

將點A1 作為參考節點,將節點振型向量按參考點振型歸一化處理[10]。全雷滿載狀態分析節點前3 階模態振型如圖5 所示(空載狀態振型類似)。

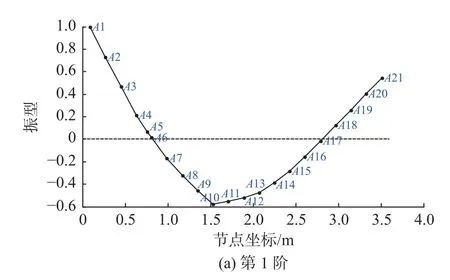
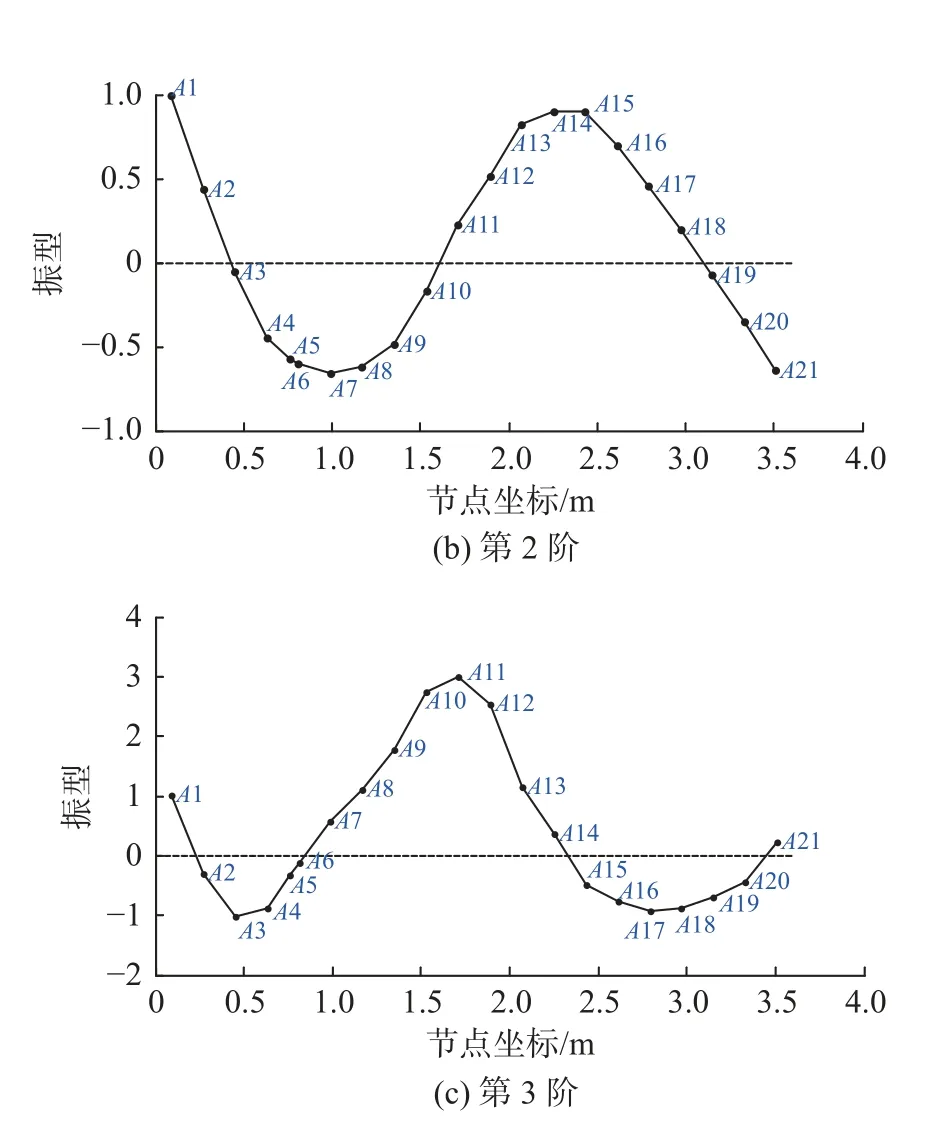
圖5 滿載狀態下全雷節點前3 階模態振型Fig.5 The first there order modal shapes of torpedo ’s Analyzed nodes at full load state

全雷節點振型向量對參考點歸一化后(取雷頭處點A1 為參考點),計算關心位置節點處的振型斜率。全雷狀態慣組安裝處振型斜率如表5 所示。

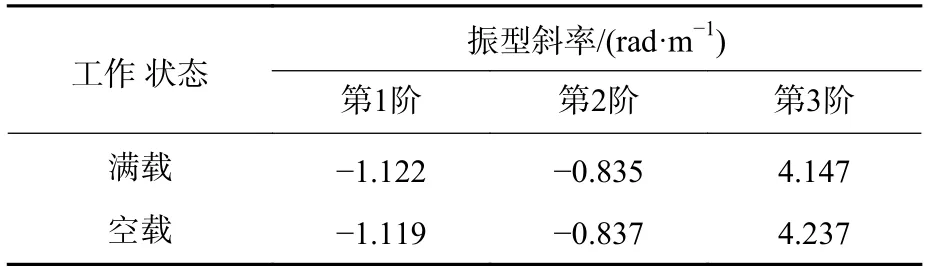
表5 慣組安裝處艙壁振型斜率Table 5 Mode shape slope of inertial navigation’s position

4 結論

文中建立了助飛魚雷動力學分析模型,并完成了助飛魚雷模態振型斜率的仿真計算,得到以下結論:

1) 助飛魚雷長細比較大,模態頻率偏小,前2 階模態頻率均小于100 Hz,其整體剛度偏小,在氣動力作用下引起的彈性振動不可忽略,姿控設計時需要考慮其影響;

2) 助飛魚雷連接結構復雜,楔環連接結構、分離艙止推塊結構以及分離艙卡箍結構影響全雷的連接剛度,進行詳細三維建模可確保動力學分析模型的正確性;

3) 通過仿真方法進行振型斜率求解時,應按照參考點進行振型歸一化處理后進行計算;

4) 參照圖5(a)和圖5(b)可以發現,前2 階模態振型斜率較大的位置在A6、A17、A3、A19 位置,這幾處位置不宜作為慣組等敏感元件的安裝位置。

通過仿真計算方法得到的振型斜率其誤差難以避免,為得到更加準確的振型斜率,仍需要根據試驗值進行模型修正,共有2 種方法:一是根據模態頻率試驗值修正,再進一步求解振型斜率;二是直接根據振型斜率值進行計算模型修正。后期將進行產品模態試驗或振型斜率測試試驗,通過試驗數據優化仿真計算方法。