基于Logistic-BP神經網絡組合模型的地鐵沉降預測研究

郝迎磊

（長春市測繪院，吉林長春130000）

0 引言

在地鐵施工過程中，可能對周邊的建筑物、道路、橋梁和地下管線等造成一定的影響，為避免地鐵施工影響周圍建（構）筑物，造成不必要的人員傷亡和財產損失，需要對基坑工程或者地鐵盾構區間一定范圍內的地表進行沉降監測，對監測數據進行分析，并研究其沉降變化規律，最后對地表沉降情況進行一定的預測。

沉降預測的方法有很多，如運用單一模型的有：朱偉剛使用BP神經網絡算法對地鐵施工過程中的地表沉降進行預測，結果表明，預測值與實測值的擬合程度較高[1]。龐逸群通過Logistic預測模型進行沉降預測，結果表明，Logistic預測模型計算得到的變形趨勢與實際工況吻合，模型預測精度較高[2]。運用組合模型的有：徐超通過灰色-BP神經網絡組合模型得到的精度高于單一模型。鄧傳軍通過PSO-BP神經網絡組合模型對建筑物的沉降情況進行預測，結果表明，PSO-BP神經網絡組合模型對建筑物沉降情況的預測結果明顯優于傳統BP神經網絡預測模型[3]。徐青提出Logistic-ARMA組合模型，結果表明，該模型能降低基坑開挖過程對地表沉降預測精度的不利影響[4]。楊帆建立了依托天牛須搜索算法優化的BASBP模型，結果表明，該組合模型較傳統BP神經網絡模型有更高的預測精度[5]。

現運用Logistic時間函數模型、BP神經網絡及Logistic-BP神經網絡組合模型，對地鐵施工過程中產生的地表沉降進行預測，最后對三種擬合模型的擬合結果進行分析。

1 Logistic時間函數模型

Logistic時間函數模型是S形曲線函數。根據圖1可知，在沉降發生階段，沉降速率緩慢增加；在沉降劇增階段，拐點將該階段分為兩個小階段，拐點前沉降速率明顯增加，拐點后沉降速率增長速度變緩；在沉降穩定階段，沉降速率增長速度緩慢降低直至不變。

圖1 Logistic時間函數模型下地鐵沉降趨勢圖

在地表沉降預測研究中，Logistic時間函數模型的函數形式如式（1）所示：

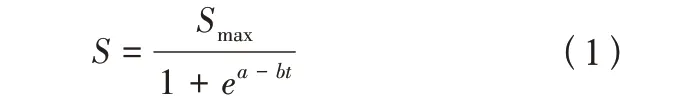
式（1）中：S為沉降量；Smax為最大沉降量；a、b為未知參數；t為時間。

此處采用三段法進行計算，需注意兩點：

第一，起算數據的期數n應為3的倍數，即每段的項數r=n/3。

第二，起算數據每期的間隔應大致相等。

在式（1）中，有三個參數需要計算，分別是Smax、a、b。三段法的參數計算方法如下：

將每段內各期沉降量的倒數求和，表示為S1、S2、S3，分別如式（2）、式（3）以及式（4）所示：

將式（1）、式（2）、式（3）、式（4）進行數學推導，得到三個未知參數的計算公式，如式（5）、式（6）、式（7）所示：

最后將計算得到的三個參數Smax、a、b帶入式（1），進而得到預測值S。

2 BP神經網絡

這里采用的是誤差反向傳播算法。由輸入層、隱含層和輸出層構成，其原理如下：將學習樣本輸入BP神經網絡結構，并設置各層之間的閾值與權值，若輸出值不理想，則反饋到網絡結構中，重新調整閾值與權值大小，從而達到減小誤差的目的，反復迭代操作，直至誤差在合理范圍內或誤差趨于穩定。

BP神經網絡學習步驟分三步：

第一，確定各層之間的初始閾值與權值的數值。

第二，計算隱含層輸出Sj，輸出值與權值乘積之和與閾值的差值在允許范圍內才可以輸出。如式（8）所示：

式（8）中：wij為第i個輸入值與第j個神經元的權值；xi為第i個輸入值；aj為隱含層第j個神經元的閾值；n為輸入層神經元個數。

第三，計算輸出層，輸出預測值yk。

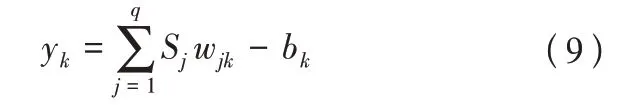
式（9）中：wjk為第j個隱含層神經元與第k個輸出層神經元的權值；bk為輸出層第k個神經元閾值；q為隱含層神經元個數。

計算出預測值yk與期望值Yk之間的差值，經過反復學習，并逐次調整閾值及權值，使預測值yk不斷逼近期望值Yk，公式如下：

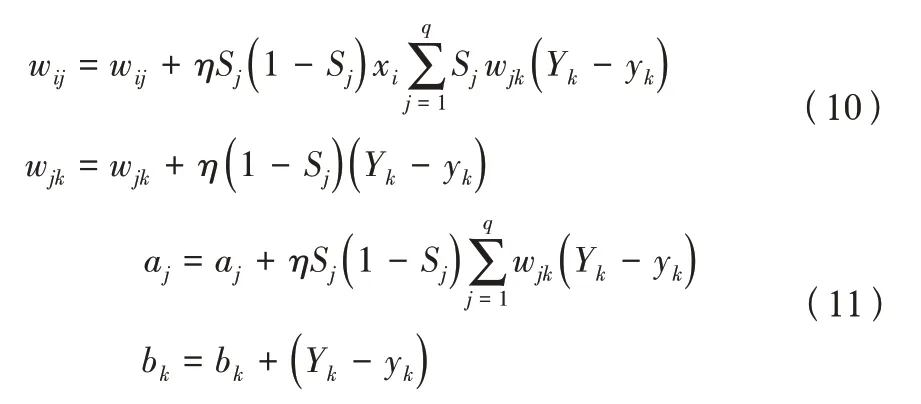
式（10）～式（11）中：η表示學習效率。

根據上述步驟，反復迭代操作，直至差值在設定誤差內或達到終止學習次數。最后將預測樣本代入式（8）、式（9）即可得到預測值。

3 Logistic-BP神經網絡組合模型

這里運用的Logistic-BP神經網絡組合模型的主要思想為：先使用Logistic時間函數模型進行擬合得到預測值，將其作為BP神經網絡的輸入數據，將實測數據作為BP神經網絡的期望輸出數據。通過反復的迭代學習，對Logistic時間函數模型的預測值不斷進行補償，使其不斷向實測值逼近，預測值趨于穩定后，則能得到效果較好的擬合值。

4 工程實例

以長春市地鐵5號線某車站的監測數據為例，運用Logistic時間函數模型、BP神經網絡及Logistic-BP神經網絡組合模型對該車站的地表沉降數據進行預測，對幾種擬合結果進行對比分析。

試驗數據來自地表沉降點，點名為DBC10-05，共計38期數據。采用前30期數據作為起算數據，預測31～38期數據。

運用三種模型擬合，結果如表1所示。

從表1結果可以看出：Logistic時間函數模型的擬合效果最差，殘差值很大，與實測值有較大偏差；BP神經網絡的擬合效果較Logistic時間函數模型好，但個別擬合值與實測值差值很大；Logistic-BP神經網絡組合模型的擬合值與實測值更接近，殘差值更小。

依據表1繪制了三種擬合模型的擬合值與實測值的對比折線圖，如圖2所示。

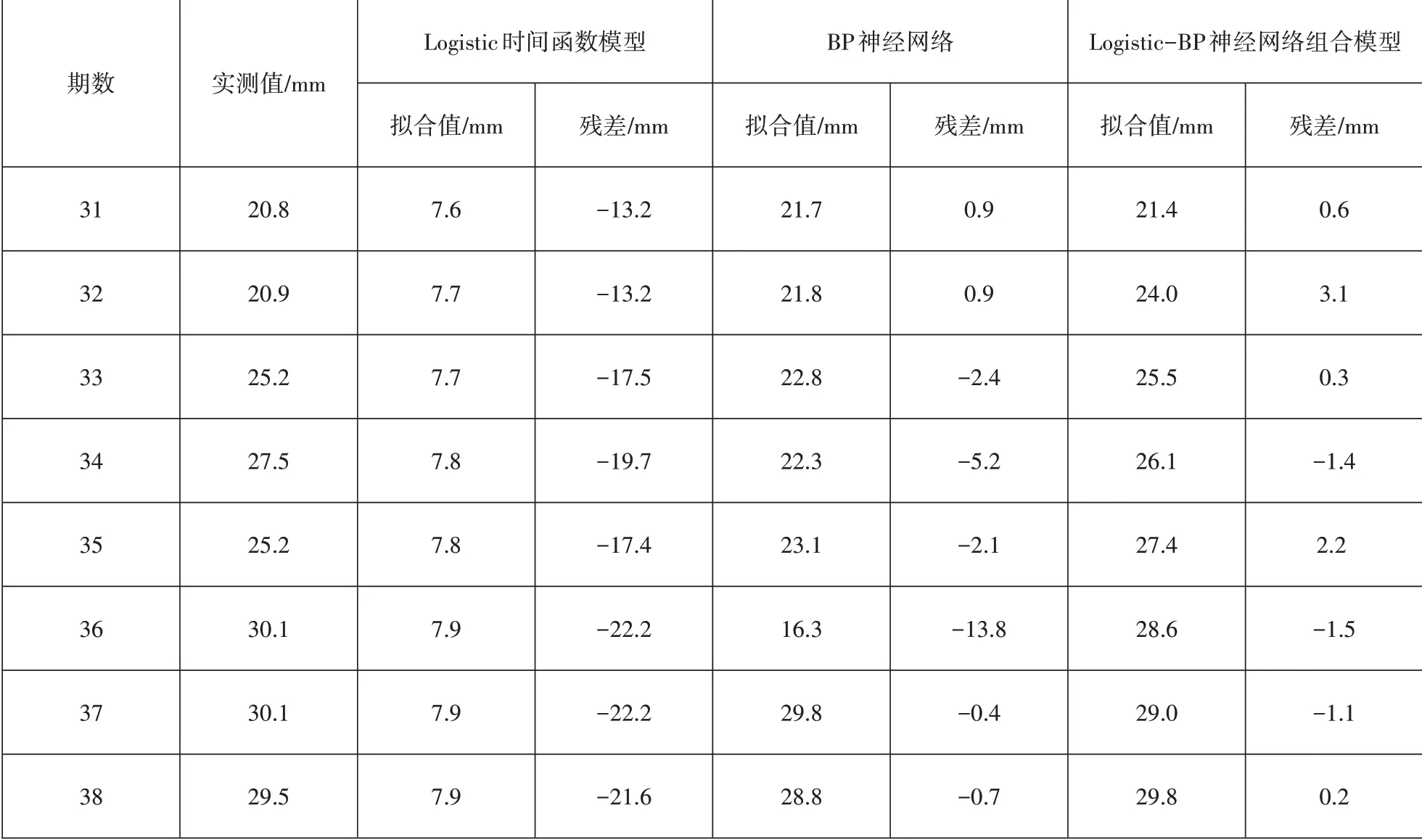
表1 三種擬合模型的擬合值及殘差值統計表

圖2 三種擬合模型的擬合值與實測值對比圖

根據圖2可以看出，Logistic-BP神經網絡組合模型的線形總體趨勢與實測值更接近。

表2所示內容為三種擬合模型的中誤差值，Logistic-BP神經網絡組合模型的中誤差明顯優于單一模型，表明運用Logistic-BP神經網絡組合模型得到的擬合值更逼近實測值。

表2 三種擬合模型的誤差統計表

5 結語

分別運用Logistic時間函數模型、BP神經網絡及Logistic-BP神經網絡組合模型，對地鐵施工過程中地表沉降點的累計值進行擬合預測，結果表明：通過Logistic時間函數模型得到的結果偏線性化，而地鐵施工過程更易受到其他非線性因素的影響，導致該模型的擬合效果較差；BP神經網絡的擬合效果較Logistic時間函數模型好，但擬合結果易出現較大波動，擬合效果穩定性低；而Logistic-BP神經網絡組合模型的擬合結果能夠更好地反映出地鐵地表的沉降變化規律，具有更多的容錯性，擬合效果較單一模型更好，預測結果較單一模型更準確、可靠，有利于對地鐵施工過程中產生的地表沉降進行更科學的預測。