基于機器視覺的對刀間隙檢測方法研究

孫齊偉，李英

（長春理工大學 光電工程學院，長春 130022）

對刀是數控機床使用中的關鍵環節，加工零件的精密度由對刀精度決定。快速準確地對刀可以大大減少加工時間，從而提高產品加工的精度。對刀的生產效率很重要。機床的對刀可分為手動對刀和自動對刀［1］。手動對刀主要是人為進行，這種操作通常占用大量工作時間并且具有較大的測量誤差，難以滿足高精度加工的要求。自動對刀功能在一定程度上大大提高了對刀效率，它易于使用、測量準確、能實現自動和實時對刀，操作者不需要技術要求，但是，高精度對刀儀成本高、安裝難度大，對刀效率的提高程度有限。

目前，計算機機器視覺技術已成為下一代智能視覺數控機床的關鍵部分，具有高精度、高效率、非接觸、智能化等優點［2-6］。于占江等人［7］利用兩個相機構建正交分布光學圖像測量系統對微小車床對刀間隙檢測，系統檢測精度達到±15μm。宋穎慧等人［8］通過LVDT對刀裝置粗定位、光學對刀裝置精定位的粗精結合的方法，快速準確地測得刀具的中心高、刀尖圓弧半徑以及刀具定心坐標，重復對刀精度達到1μm，實現精確對刀。HOU B等人［9］開發了數控機床計算機視覺自動對刀系統，該系統具有簡單高效的對刀過程，重復對刀精度小于1μm。然而對于小尺寸工件的加工，此方法不能保證相機垂直拍攝工件xy面。

機器視覺測量容易受到環境的干擾，視場光照不均，目標表面反光等因素會影響視覺測量的準確度和精確度。本文通過頂帽變換、線性加深、圖像分塊、區域生長等操作一定程度上消除了光照不均和目標反光的問題，實現了目標的完整提取。本文利用基于機床坐標信息反饋的視覺系統標定方法［9］實現了相機高精度標定，并運用到機床對刀間隙檢測中，精確有效地實現了機床對刀間隙的識別與檢測。

1 系統總體方案設計

數控機床視覺對刀系統主要由光源、CCD圖像采集模塊、計算機處理系統、控制執行系統等構成。實驗平臺如圖1所示。1號和2號CCD沿垂直刀具方向安裝，兩個CCD相互垂直安裝。CCD模塊采用IMPERX_bobcat-B2520工業相機，性能參數如表1所示。鏡頭采用微視的AFTZML1011工業放大鏡頭，性能參數如表2所示。數控機床分辨率為1μm，視覺系統精度預計為1μm。視場約為14 mm×12 mm，計算出的每個像素精度約為5.70μm。然后使用Zernike moments檢測，由于Zernike moments亞像素邊緣提取比傳統的canny等像素級算法精度提高5～8倍［10］，理論像素精度應該達到1.140μm。

表1 相機性能參數

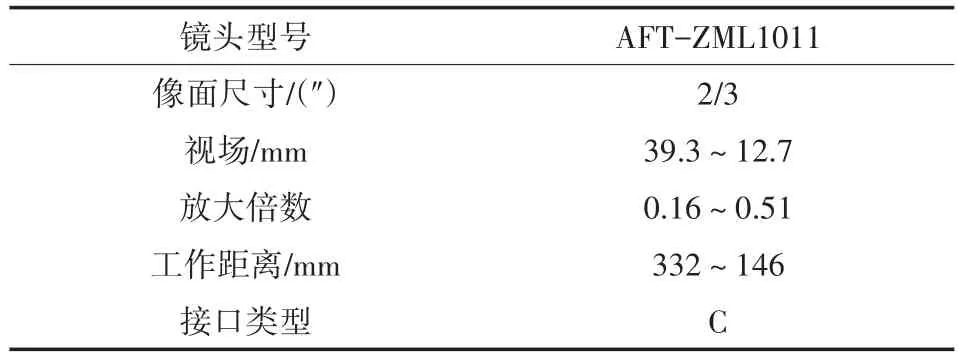
表2 鏡頭性能參數

圖1 實驗平臺

在系統中，采用白色光源照射間隙部位，CCD相機將獲取的間隙圖像經由圖像采集卡傳送至PC機。計算機系統利用圖像處理算法對獲取的數字圖像進行各種處理運算，提取出刀具與工件的間隙值，并以指令方式控制機床微動平臺進給。

2 相機標定

在進行對刀時，要盡量使刀位點和對刀點相互重合［11］，即刀位點與對刀點的位置偏差為零。刀位點是確定刀具位置的基準點，一般選擇刀具的刀尖。對刀點是指刀具相對于工件加工運動的起點。本文選擇矩形工件的一角點作為對刀點，對刀過程此時指刀具的刀尖運動到工件的一個角點上。鑒于機床的高分辨率，本文采用基于機床坐標信息反饋的視覺系統標定方法對相機進行標定，該方法不需要安裝特殊的校準位移測量系統。因此，標定過程簡單高效，有利于可視化對刀的工程應用。

標定過程如圖2所示，1號相機捕捉xz面，dx為對刀點與刀位點x方向的偏移距離，dz為刀位點到工件表面z方向的距離；2號相機捕捉yz面，dy為對刀點與刀位點y方向的偏移距離，dz同上。機床每次沿X/Y/Z方向移動100μm，記為Dm，對相應方向的距離進行圖像采集和計算，求出偏移距離Dc（單位：pixel），則可計算出相機的標定系數，公式如下：

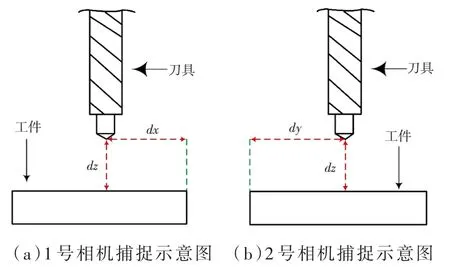
圖2 相機捕捉示意圖

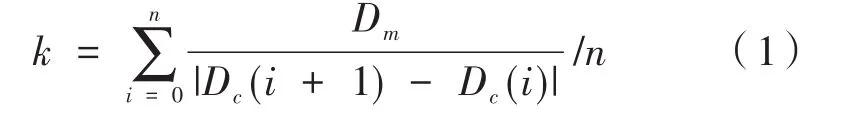
式中，Dc（i）是第i次計算出的偏移距離。

為了提高相機標定的精確度，多次重復實驗，部分數據如表3所示，則可得出相機的標定系數為：

表3 X/Y，Z軸偏移距離

3 對刀間隙檢測

3.1 對刀間隙檢測流程

對刀間隙檢測流程如圖3所示，其中圖像處理階段流程如圖4所示。兩個相同的相機參數相同，調整刀具與工件的偏移距離，通過相機獲取的對刀間隙如圖5、圖6所示。

圖3 對刀間隙檢測流程圖

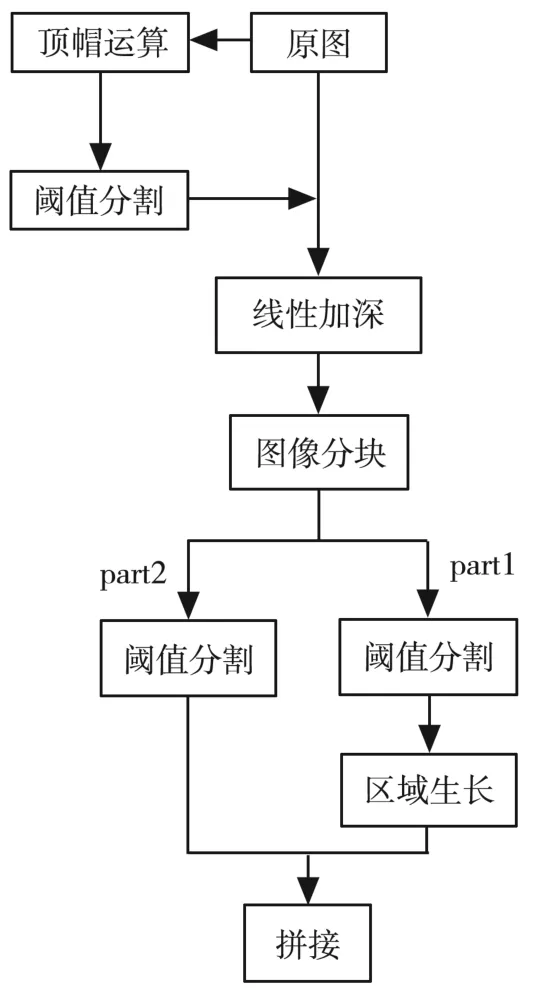
圖4 圖像處理流程圖

圖5 1號相機捕捉圖

圖6 2號相機捕捉圖

3.2 圖像處理

相機采集的圖像光照不均勻，刀具還存在反光現象，嚴重影響對刀具和工件的識別。為了完整提取刀具和工件需要進行一系列處理，處理過程如圖4所示。

3.2.1 頂帽變換

圖5、圖6所示顯示圖像右上方的背景比左下方的背景亮，且刀具有反光。對不均勻亮度圖像做閾值處理很困難，不能很好地將目標從背景中分離。對圖像進行開運算可以產生對整個圖像背景的合理估計。從原圖像中減去開運算后的圖像，可以生成一副具有合適且均勻的背景的目標圖像，如圖7所示。圖中背景較均勻，目標輪廓較模糊，需要進一步分離背景與目標。經過閾值分割后如圖8所示。從中可以看出，目標的輪廓大體上被提取出來了，刀具反光部分比較明顯。由此，可以利用此圖作為刀具反光部分的掩膜，去除刀具的反光。

圖7 頂帽變換圖

圖8 頂帽圖二值化

從原圖像中減去開運算后的圖像稱為頂帽變換，公式如下：

式中，f為原圖；°為開運算；b為結構元素。

3.2.2 線性加深

將原圖像與閾值分割頂帽變換的圖像進行線性加深，如圖9所示。

圖9 線性加深圖

線性加深的算法如下：

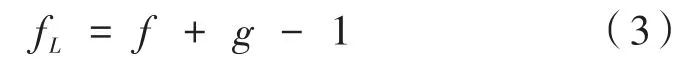
其中，fL為輸出圖像的像素值；f、g分別為兩幅圖像的像素值。如果兩幅圖像的像素值之和小于255，輸出結果將會是純黑。如果將其中一幅圖像反相，結果將是純粹的數學減。

從圖9中可以看出，刀具反光部分被彌補，背景部分亮度不均勻，不能對整體圖像做閾值分割。

3.2.3 區域生長

本文對圖9進行上下分塊，之后分別進行閾值分割，如圖10（a）、圖10（b）所示。

圖10 分塊二值圖

圖10（a）中刀具與背景沒有完全分離，因此，本文采用區域生長方式提取刀具。區域生長是根據預先定義的生長準則，將像素或子區域組合為更大區域的過程。基本方法是從一組“種子”點開始，將與種子預先定義的性質相似的那些領域像素添加到種子上，來形成這些生長區域（如特定范圍的灰度或顏色）。本文選取刀具中心線附近一點作為“種子”，進行區域生長來分割圖像，生長閾值根據實驗條件確定。實驗結果如圖11所示。

圖11 刀具提取圖

之后將圖11和圖10（b）按照圖像分塊之前的位置進行拼接，如圖12所示。

圖12 拼接圖

3.3 邊緣檢測

為了高精度提取刀具和工件特征，本文采用Zernike moments［12］提取圖像邊緣。

圖像的f（x，y）的n階m次 Zernike moments定義為［13］：

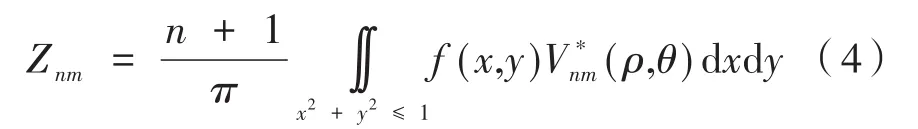
式 中，Vnm（ρ，θ）是積分函數，表示與Vnm(ρ,θ)共軛，m、n都為整數且滿足：n≥0，n-|m|為偶數且n≥|m|。

假設單位圓的圓心位于圖像的某個像素點上，并且圖像邊緣經過該圓，由此建立理想的階躍邊緣模型，如圖13所示。

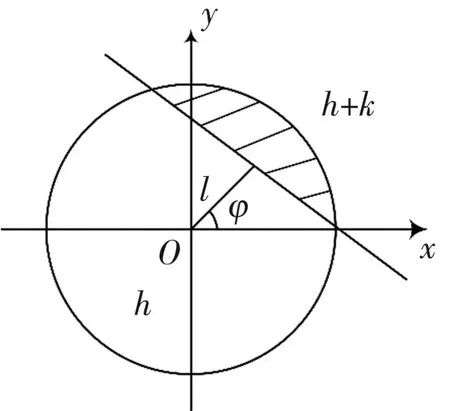
圖13 理想階躍邊緣

圖13中，k是階躍灰度，h是背景灰度，則陰影部分的灰度值為h+k；l是圓心到邊緣的垂直距離；φ是邊緣垂線與x軸的夾角。將圖像順時針旋轉φ角度，使邊緣平行于y軸，如圖14所示。旋轉后的理想階躍邊緣模型的側面剖析圖呈階梯狀，如圖15所示。

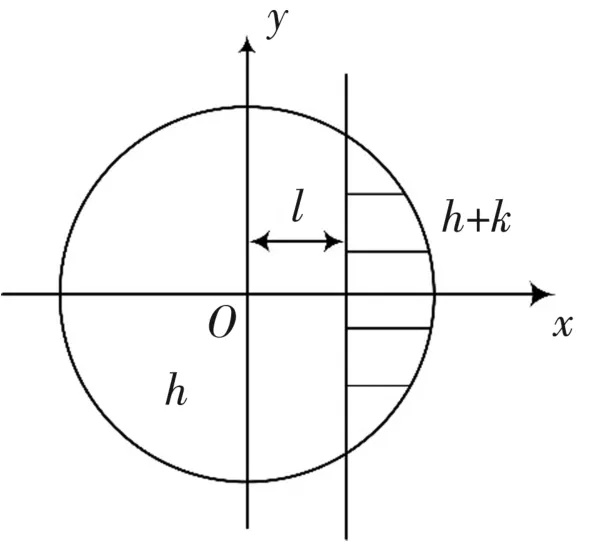
圖14 旋轉后的理想階躍邊緣

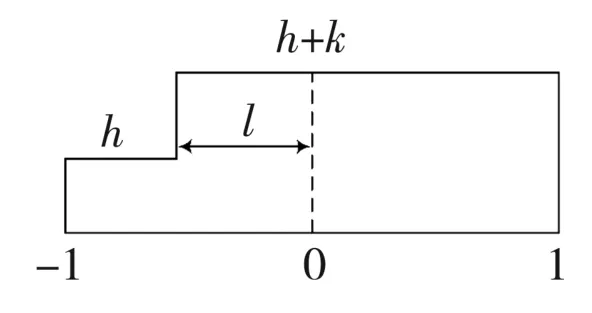
圖15 理想階躍邊緣剖面

設旋轉后的圖像為f′（x，y），則由于旋轉后的圖像關于x軸對稱，則：

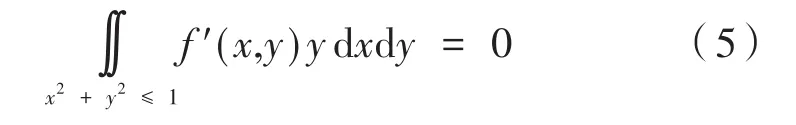
由于式（5）就是Z′11的虛部，所以存在以下關系：

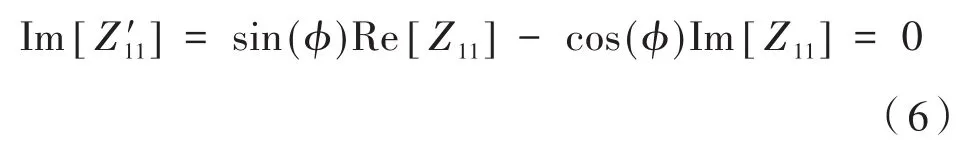
由式（6）可求得圖像旋轉角度為：

Zernike moments的一個重要性質是旋轉不變性。若一幅圖像旋轉φ角，則旋轉前后的Zernike moments只有相角改變，幅值仍保持不變，即：

Z00、Z11和Z20對應的積分核為V00=1，V11=x+jy，V20=2x2+2y2+1，結合圖16，可以推導出旋轉后圖像的各階Zernike moments。

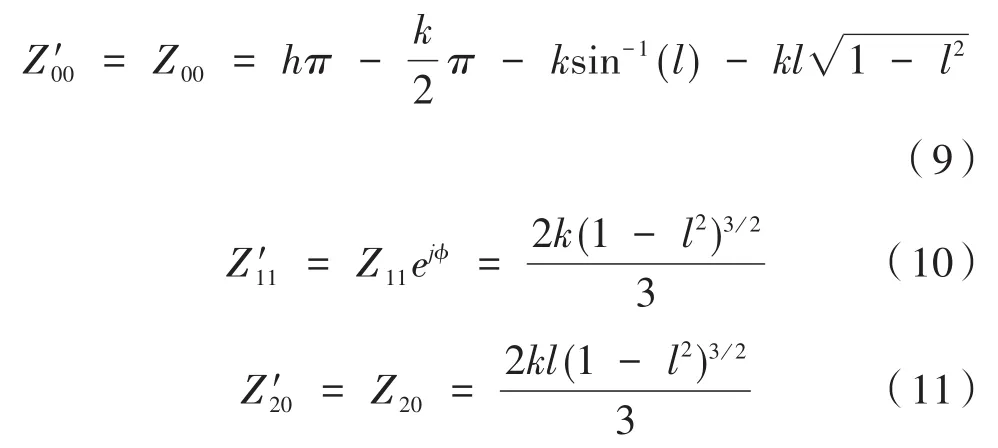
由式（9）～式（11）解得參數l、k為：

假設在邊緣檢測過程中采用的模板大小為N×N，結合其放大效應的修正，可以得到利用Zernike moments進行亞像素邊緣檢測的計算式：

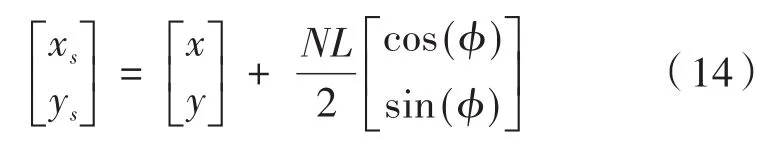
其中，（xs，ys）是邊緣的亞像素坐標值；（x，y）是圖13中的某個像素點，也是單位圓圓心。

本文采用模板大小為7×7的Zernike moments提取目標的亞像素邊緣，如圖16所示。

圖16 亞像素邊緣提取圖

3.4 對刀間隙距離計算

經過邊緣檢測后，刀具和工件的邊緣輪廓可以清晰地提取出來，然后Hough直線變換求出工件圖像上的邊緣直線方程：

同時刀具的輪廓下邊緣可以檢測出多個像素點（x，y），根據點到直線的距離方程計算出Z方向刀尖點到對刀平面直線的距離。

其中，D是像素點（x，y）到直線方程的距離。通過比較點到直線的距離的大小，來判斷刀具的刀尖點，選擇距離最小的相對應的點的像素縱坐標作為刀具刀尖的縱坐標。選擇刀具兩條直邊的中心線的橫坐標作為刀具刀尖的橫坐標。利用點到直線的公式可計算出x，y方向上的對刀間隙。

4 實驗結果分析

實驗中，通過機床平臺施加微小位移進行系統驗證，在實際測試中，刀具在平臺的帶動下按相同位移間隔進行移動，接近待加工工件的對刀點。通過相機獲得刀具圖像，分別用本算法和于占江等人［7］提出的算法（簡稱“于算法”）測量刀具偏移距離。測量數據如圖17（a）、17（c）、17（e）所示，測量誤差如圖 17（b）、17（d）、17（f）所示。從測量誤差圖中可知，本算法的測量誤差比于算法的測量誤差較小，說明了本算法的檢測精度高。在視場約為14 mm×12 mm中，用于算法中相機標定的方法進行標定，相機的水平標定系數為5.93μm/pixel，垂直標定系數為6.84μm/pixel，相機標定精度較低。此外，于算法在像素上進行圖像處理，檢測精度相比亞像素檢測精度較低，所以于算法的測量誤差相比本算法較高。本算法的測量誤差在±2μm以內，造成誤差的因素有刀面線擬合時不夠精確，刀具抖動。

圖17 X、Y、Z方向測量數據及誤差圖

通過記錄多次視覺系統運行時間，如圖18所示。視覺系統的圖像采集和處理所需的時間約為2.26 s，準確性達到了現代制造業的要求，系統速度還有待提高。

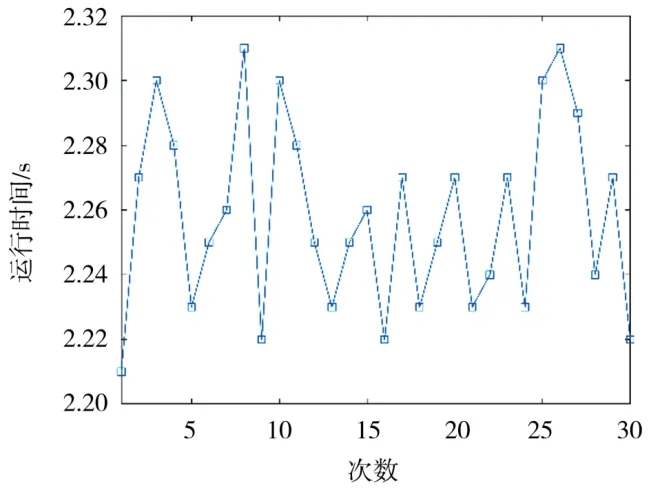
圖18 視覺系統運行時間

5 結論

本文設計了一種應用于小尺寸工件加工的三維對刀間隙檢測裝置。通過本文圖像處理部分的算法一定程度上消除了目標反光和光照不均的影響，完成了目標的完整精確提取。采用基于機床坐標信息反饋的視覺系統標定方法完成了視覺系統的標定，并實現了對刀間隙的精確測量。通過機床實驗平臺施加微小位移進行系統驗證，實驗結果表明：該檢測系統能夠快速有效地進行數控機床對刀間隙識別與檢測，系統檢測精度達±2μm，圖像處理的時間消耗為2.26 s，系統的準確性達到了現代制造業的要求，系統速度還有待提高。