一種基于改進(jìn)鄰域粗糙集中屬性重要度的快速屬性約簡(jiǎn)方法

周長(zhǎng)順,徐久成,瞿康林,申凱麗,章 磊

(1.河南師范大學(xué) 計(jì)算機(jī)與信息工程學(xué)院,河南 新鄉(xiāng) 453007;2.智慧商務(wù)與物聯(lián)網(wǎng)技術(shù)河南省工程實(shí)驗(yàn)室,河南 新鄉(xiāng) 453007)

冗余屬性是影響分類算法運(yùn)行速度和分類精度的重要因素[1], 所以進(jìn)行屬性約簡(jiǎn)對(duì)提高分類算法的性能有著重要意義[2-3]。 針對(duì)屬性約簡(jiǎn), 常用的有主成分分析法, 相關(guān)性分析法和Hu等人提出的可針對(duì)連續(xù)性變量進(jìn)行屬性約簡(jiǎn)的鄰域粗糙集屬性約簡(jiǎn)算法[4-6]。 主成分分析法和相關(guān)性分析法會(huì)導(dǎo)致原始數(shù)據(jù)中信息丟失, 而鄰域粗糙集在進(jìn)行屬性約簡(jiǎn)時(shí), 可在保留數(shù)據(jù)集內(nèi)部信息和分類能力的同時(shí)消除原始數(shù)據(jù)集中重復(fù)和冗余的特征[4]。 基于鄰域粗糙集的屬性約簡(jiǎn)算法在進(jìn)行屬性約簡(jiǎn)計(jì)算時(shí)， 主要有兩個(gè)步驟需占用大量時(shí)間, 即第一步正域的計(jì)算和第二步屬性重要度的計(jì)算。 文獻(xiàn)[2]提出了屬性約簡(jiǎn)算法FARNeMF(forward attribute reduction based on neiborhood rough sets and fast search[2]),FARNeMF在進(jìn)行正域計(jì)算時(shí)不需對(duì)樣本重復(fù)計(jì)算正域,減少了正域計(jì)算中樣本計(jì)算次數(shù)。文獻(xiàn)[7]在FARNeMF的基礎(chǔ)上提出了快速哈希屬性約簡(jiǎn)算法(fast hash attribute reduct algorithm,FHARA)[7],為減少樣本計(jì)算次數(shù), 該算法通過(guò)對(duì)原始樣本進(jìn)行劃分, 在正域計(jì)算中只計(jì)算鄰域和相同域內(nèi)且未加入到正域的樣本, 進(jìn)一步減少了正域計(jì)算的時(shí)間。 以上所提的改進(jìn)算法減少了正域計(jì)算的時(shí)間, 然而在屬性重要度計(jì)算時(shí), 計(jì)算次數(shù)并沒有減少。

上文所提的FHARA等算法在屬性重要度計(jì)算時(shí)是貪心式的, 其計(jì)算步驟如下, 如針對(duì)有N個(gè)條件屬性的數(shù)據(jù)集, 求加入約簡(jiǎn)集的第一個(gè)屬性時(shí), 需要對(duì)N個(gè)條件屬性計(jì)算正域, 選取正域最大的一個(gè)條件屬性加入到約簡(jiǎn)集中, 加入第二個(gè)屬性時(shí)需要對(duì)N-1個(gè)條件屬性進(jìn)行正域計(jì)算[8-10], 針對(duì)FHARA等屬性約簡(jiǎn)算法計(jì)算屬性重要度消耗時(shí)間過(guò)多, 尤其是面對(duì)高維數(shù)據(jù)時(shí)會(huì)消耗大量時(shí)間的問(wèn)題, 本文提出了一種基于改進(jìn)KNN屬性重要度的鄰域粗糙集屬性約簡(jiǎn)算法(KNN of fast hash attribute reduct algorithm, KFHARA),該算法首先在FHARA的基礎(chǔ)上給出一種新的鄰域粗糙集屬性重要度方法,利用該方法對(duì)數(shù)據(jù)集條件屬性進(jìn)行排序時(shí)，只需對(duì)條件屬性集計(jì)算一次屬性重要度。利用排序好的屬性重要度,約簡(jiǎn)集每加入一個(gè)條件屬性只需要計(jì)算一次正域,減少了算法的運(yùn)行時(shí)間。

1 相關(guān)工作

1.1 鄰域粗糙集

設(shè)NDS=〈U,C∪D,δ〉是一個(gè)鄰域粗糙集決策系統(tǒng),U=(x1,x2,…,xn)代表存在n個(gè)樣本的集合,C=(a1,a2,…,aN)是全部樣本的條件屬性集合,B?C,N代表特征數(shù)量,D為決策屬性集，xi(i=1,…,n)為樣本空間中的點(diǎn)。

定義1[1]任意xi∈U,定義xi的鄰域?yàn)?/p>

δB(xi)={x|x∈U,ΔB(xi,x)≤δ}

(1)

其中,ΔB(xi,x)表示點(diǎn)之間的距離函數(shù)。δB(xi)表示與樣本xi在條件屬性集B中取值在一定范圍內(nèi)的點(diǎn),即在樣本空間中與xi距離處于預(yù)設(shè)半徑范圍內(nèi)的樣本子集,稱為x的鄰域距離函數(shù)通常采用范數(shù)距離公式。

定義2[2]任意屬性,Minkowski距離公式為

f(x2,ai)|P)1/P

(2)

定義2是相對(duì)于數(shù)值型屬性的,但鄰域概念可很容易地將數(shù)值計(jì)算擴(kuò)展到實(shí)值數(shù)據(jù)。

定義3[2]設(shè)dai(x,y)為樣本點(diǎn)x和y在屬性ai上的函數(shù)

(3)

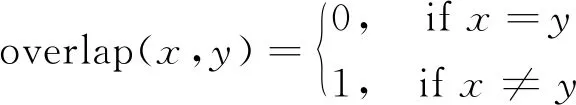
(4)

定義3中可同時(shí)處理數(shù)值型和名義型屬性,即使樣本屬性的類型或者取值dai(x,y)未知時(shí)也可以使用。

定義4[2]鄰域粗糙集上、下近似、邊界域分別定義為

(5)

(6)

(7)

其中，X?U。

定義5[1]B?C,B相對(duì)于D的鄰域依賴度γB(D)定義為

(8)

1.2 鄰域粗糙集的屬性約簡(jiǎn)

鄰域粗糙集進(jìn)行屬性約簡(jiǎn)時(shí),每個(gè)屬性的重要度由該屬性增加正域的大小來(lái)確定,屬性加入的正域越大屬性重要度越高。鄰域粗糙集屬性約簡(jiǎn)算法的流程可簡(jiǎn)單描述為:將約簡(jiǎn)集合初始為空集,將當(dāng)前條件屬性集合中增加最大正域的一個(gè)屬性加入到約簡(jiǎn)屬性集合中,每增加一個(gè)屬性就需對(duì)未加入到約簡(jiǎn)集合的每個(gè)條件屬性計(jì)算一次正域[11-13]。例如,目前有N個(gè)待約簡(jiǎn)的條件屬性,樣本個(gè)數(shù)為Q,約簡(jiǎn)集每加入一個(gè)屬性增加的正域個(gè)數(shù)為ki(i=1,…,k-1),約簡(jiǎn)集合第一次添加屬性時(shí)需要對(duì)所有條件屬性進(jìn)行正域計(jì)算,計(jì)算次數(shù)為N,加入第二個(gè)條件屬性時(shí)計(jì)算正域次數(shù)為(N-1),以此類推,如果約簡(jiǎn)后的集合有k個(gè)屬性，那么正域計(jì)算次數(shù)為

(N+(N-1)+…+(N-k+1))

(9)

計(jì)算第k個(gè)屬性正域的時(shí)間為Posk,那么鄰域粗糙集屬性約簡(jiǎn)算法的時(shí)間復(fù)雜度為

Q×N×Pos1+(Q-k1)×(N-1)×Pos2+

…+(Q-kk-1)×(N-k+1)×Posk

(10)

上文所提的傳統(tǒng)鄰域粗糙集屬性約簡(jiǎn)算法在屬性約簡(jiǎn)計(jì)算中有很多關(guān)于正域的重復(fù)計(jì)算。為減少鄰域粗糙集屬性約簡(jiǎn)中正域計(jì)算次數(shù),文獻(xiàn)[7]提出了FHARA算法如圖1所示，它利用桶劃分的方式將樣本空間利用距離因子δ映射劃分成一個(gè)個(gè)的扇形區(qū)域,在計(jì)算正域時(shí)，無(wú)需對(duì)所有樣本進(jìn)行計(jì)算,只需對(duì)本鄰域和相鄰鄰域的且未加入正域的樣本進(jìn)行正域計(jì)算。

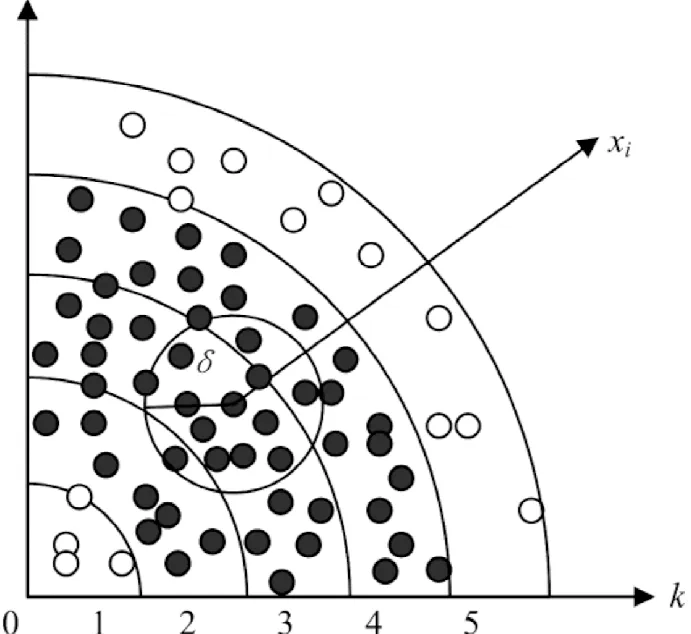
圖1 FHARA正域計(jì)算示意圖

2 基于改進(jìn)屬性重要度的約簡(jiǎn)算法

2.1 改進(jìn)的KNN屬性重要度

根據(jù)上節(jié)鄰域粗糙集屬性約簡(jiǎn)算法的相關(guān)知識(shí),可知鄰域粗糙集屬性約簡(jiǎn)算法的時(shí)間復(fù)雜度與每次正域計(jì)算時(shí)間和正域計(jì)算次數(shù)有關(guān),FHARA算法通過(guò)對(duì)原始數(shù)據(jù)進(jìn)行桶劃分,將數(shù)據(jù)利用距離因子δ分成一層層的桶,在計(jì)算正域時(shí)對(duì)本層和相鄰層的樣本進(jìn)行正域計(jì)算,在面對(duì)樣本數(shù)較多的數(shù)據(jù)時(shí)可有效減少正域計(jì)算時(shí)間,降低時(shí)間復(fù)雜度。目前有很多基于正域重要度來(lái)對(duì)屬性進(jìn)行重要度排序的算法,如基于信息熵重要度的算法和基于屬性相關(guān)性的算法,這些算法在進(jìn)行屬性重要度判斷時(shí)，時(shí)間并沒有減少[14]。為了減少屬性重要度的計(jì)算時(shí)間,本文提出一種快速屬性約簡(jiǎn)算法KFHARA。 KFHARA在FHARA算法的基礎(chǔ)上給出一種基于改進(jìn)KNN屬性重要度的屬性約簡(jiǎn)算法,改進(jìn)后的算法在對(duì)屬性個(gè)數(shù)為N的數(shù)據(jù)集進(jìn)行屬性重要度排序時(shí)，計(jì)算量從N2降為N。該算法進(jìn)行屬性約簡(jiǎn)時(shí)，只需進(jìn)行一次屬性重要度計(jì)算即可獲得所有條件屬性的重要度排序。對(duì)于一個(gè)數(shù)據(jù)集,樣本個(gè)數(shù)為Q,屬性個(gè)數(shù)為N,樣本間距離定義如下。

定義6在N維實(shí)數(shù)空間RN上,空間中任意兩點(diǎn)xi=(xi1,xi2，…，xiN)與xj=(xj1,xj2，…，xjN)的距離d(xi,xj)為

(11)

按照定義6中公式計(jì)算距離矩陣d,d是一個(gè)U×U的對(duì)稱矩陣,主對(duì)角線元素為0,d[i,j](i=1,…,m;j=1,…,m)代表點(diǎn)xi與xj間的距離。首先在Q個(gè)樣本中抽取h個(gè)樣本,為了保證抽樣結(jié)果的不失真[15],需對(duì)每一類數(shù)據(jù)都抽取相同個(gè)數(shù)的樣本,設(shè)數(shù)據(jù)集分類結(jié)果的種類為g,則在每一類中抽取(h/g)個(gè)樣本。對(duì)抽取的每一個(gè)樣本,根據(jù)距離矩陣d求距離該樣本最近的k個(gè)同類樣本和k個(gè)異類樣本,并求它們的距離序列。

定義7在N維實(shí)數(shù)空間RN上,空間中任意兩點(diǎn)xi=(xi1,xi2，…，xiN)與xj=(xj1,xj2，…，xjN)的距離序列dt(xi,xj)的計(jì)算公式為

dt(xi,xj)=|(xi1-xj1,xi2-xj2,…,xiN-xjN)|

(12)

對(duì)于經(jīng)式(12)計(jì)算得到的所有距離序列dt,same和dt,false,這兩個(gè)距離序列都為h×g行、N列。

(13)

(14)

其中：xy(j=1,…,h)代表抽取的h個(gè)樣本；xp(y=1,…,k),xq(y=1,…,k)分別代表距離每個(gè)抽取樣本最近的k個(gè)同類和異類樣本；dt,same和dt,false分別按列求和,得到兩個(gè)長(zhǎng)度為N的一維數(shù)組dsame和dfalse,數(shù)組中N個(gè)元素代表所抽取樣本在N個(gè)條件屬性上的距離和。將dfalse和dsame按位相除即dfalse/dsame得到長(zhǎng)度為N的屬性重要度序列Sig,dfalse,i和dsame,i分別為為dfalse和dsame的第i個(gè)屬性,第i個(gè)屬性的重要度Sigi即為

(15)

約簡(jiǎn)定義如下:在進(jìn)行屬性約簡(jiǎn)時(shí),將約簡(jiǎn)集初始為空,根據(jù)屬性重要度Sig,每次把重要度最大的屬性加入約簡(jiǎn)集,對(duì)加入該屬性之后的約簡(jiǎn)集合進(jìn)行正域計(jì)算,若所得正域大于零,將該屬性加入約簡(jiǎn)集并加入新的屬性進(jìn)行下一次正域計(jì)算;若所得正域等于零,結(jié)束運(yùn)算舍棄當(dāng)前屬性,輸出約簡(jiǎn)集合。

改進(jìn)的KNN屬性重要度(式(15)計(jì)算的Sig)的含義為:對(duì)于在每個(gè)類上平均抽取的h個(gè)樣本的最近的k個(gè)同類樣本和最近的k個(gè)異類樣本,計(jì)算他們?cè)诿總€(gè)屬性上的距離,在每一個(gè)屬性上,分別對(duì)得到的所有同類樣本點(diǎn)的距離求和,所有異類樣本點(diǎn)的距離求和得到長(zhǎng)度為N的數(shù)組dsame,dfalse。對(duì)某一屬性i(i=1,…,N)來(lái)說(shuō),dsame[i]越小,代表同類樣本在這一屬性上越集中,該屬性越利于分類,dfalse[i]越小,代表不同類樣本在這一屬性上越集中,該屬性越不利于分類。基于此,構(gòu)建屬性重要度函數(shù)Sig=dfalse/dsame,將dfalse置于分子的位置,將dsame置于分母的位置,若某一屬性的Sig越大,代表該屬性越有利于分類,屬性重要度就越大。KFHARA和FRABVAL[16](fast attribute reducation algorithm based on importance of voting attribute)算法相比,KFHARA算法無(wú)需遍歷所有樣本來(lái)進(jìn)行屬性重要度的排序,只需通過(guò)所抽取的h個(gè)樣本計(jì)算屬性重要度,減少了算法運(yùn)行的時(shí)間;其次,FRABVAL算法在計(jì)算重要度時(shí)只選取最近的一個(gè)同類和異類樣本,可能會(huì)受噪聲點(diǎn)的影響,而KFHARA算法選取k個(gè)同類和異類樣本進(jìn)行的計(jì)算減少了噪聲點(diǎn)的影響。同時(shí)，為了防止所抽取的數(shù)據(jù)失真,在每一類數(shù)據(jù)上均勻采樣;FRABVAL算法在對(duì)屬性重要度排序時(shí)是投票式,按照所得屬性距離順序每一個(gè)屬性都比前一個(gè)屬性加1,KFHARA算法對(duì)樣本屬性之差再求和,保留了更多數(shù)據(jù)的原始信息。

2.2 基于改進(jìn)KNN屬性重要度的KFHARA算法

結(jié)合2.1提出的改進(jìn)的KNN屬性重要度,構(gòu)建KFHARA算法,第一步先求屬性重要度Sig。

算法1基于改進(jìn)KNN的屬性重要度算法

輸入:數(shù)據(jù)集Data,包含條件屬性C決策屬性D,樣本總個(gè)數(shù)n,樣本抽樣次數(shù)h,條件屬性個(gè)數(shù)N,分類類別數(shù)g,最近樣本個(gè)數(shù)k。

輸出:屬性重要度集合Sig。

1) fori=1:n

forj=i:n/*求樣本間的距離*/

d(xi,xj)/*計(jì)算樣本間的距離*/

d(xj,xi)=d(xi,xj)

end for

end for;

2) fora=1:g/*對(duì)每個(gè)類抽取(h/g)個(gè)樣本*/

fors=1:h/g

x=x.append(xs)

end for

end for;

3) forw=1:h/*對(duì)抽取到的樣本求距離序列*/

fore=1:k

dsame(xw,xe)/*計(jì)算同類樣本序列*/

dfalse(xw,xe)/*計(jì)算異類樣本序列*/

end for

end for;

4) foro=1:N/*對(duì)得到的序列按列求和*/

dsame=dsame+dsame,i

dfalse=dfalse+dfalse,i

end for;

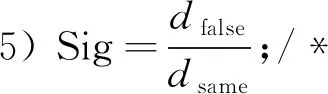
6) Sort(Sig);/*對(duì)屬性重要度進(jìn)行排序*/

7) return Sig./*輸出屬性重要度*/

第二步利用求得的屬性重要度進(jìn)行屬性約簡(jiǎn)見算法2。

算法2屬性約簡(jiǎn)算法

輸入:數(shù)據(jù)集Data,包含條件屬性C,決策屬性D屬性重要度Sig,距離因子δ。

輸出:約簡(jiǎn)集合reduce。

1) 初始化reduce=?,pos=?,pos-tag=[0];/*初始化*/

2) forv=1:N

pos=Pos(pos-tag,[reduce,Csig[v]])/*計(jì)算正域*/

if pos≠?/*屬性增加正域加入約簡(jiǎn)集*/

reduce=[reduce,Csig[v]]

pos-tag=update(pos-tag,pos)/*更新標(biāo)志位*/

else

break

end for;

3) return reduce./*輸出約簡(jiǎn)集*/

KFHARA屬性重要度算法時(shí)間復(fù)雜度為

(16)

KFHARA算法的總時(shí)間復(fù)雜度為:

Pos1+Pos2+…+Posk

(17)

與改進(jìn)前的鄰域粗糙集屬性約簡(jiǎn)算法相比(公式(10))KFHARA算法大大減少了計(jì)算量。KFHARA算法流程圖如圖2所示。

圖2 KFHARA算法流程

3 實(shí)驗(yàn)結(jié)果與分析

3.1 實(shí)驗(yàn)準(zhǔn)備

本實(shí)驗(yàn)使用Python語(yǔ)言,基于Pycharm環(huán)境,為驗(yàn)證本文提出的KFHARA算法的效果,從UCI數(shù)據(jù)庫(kù)中選取7組公開數(shù)據(jù)集進(jìn)行實(shí)驗(yàn),經(jīng)過(guò)實(shí)驗(yàn)驗(yàn)證本方法中的k取4時(shí),得到的約簡(jiǎn)集合具有較好的分類效果。表1 是對(duì)實(shí)驗(yàn)所用數(shù)據(jù)集描述。

表1 數(shù)據(jù)集描述

在進(jìn)行實(shí)驗(yàn)時(shí)鄰域閾值δ的選取非常重要,本文使用文獻(xiàn)[16]中的方法,每個(gè)條件屬性上的δ等于這一條件屬性的標(biāo)準(zhǔn)差。

3.2 實(shí)驗(yàn)算法驗(yàn)證

為了驗(yàn)證KFHARA算法的有效性,將KFHARA算法與FHARA, FRABVA和F2HARNRS[17](neighborhood rough set based hetergenerous future subset selection)等基于鄰域粗糙集的屬性約簡(jiǎn)算法進(jìn)行對(duì)比。實(shí)驗(yàn)采用10折交叉驗(yàn)證,通過(guò)實(shí)驗(yàn)結(jié)果對(duì)比,證明了本文提出的KFHARA算法的有效性。

3.2.1 算法運(yùn)行時(shí)間對(duì)比 表2和圖3顯示了對(duì)比算法和所提出的KFHARA算法在7個(gè)數(shù)據(jù)集下的平均運(yùn)行時(shí)間,時(shí)間以s為單位。

表2 算法運(yùn)行時(shí)間對(duì)比

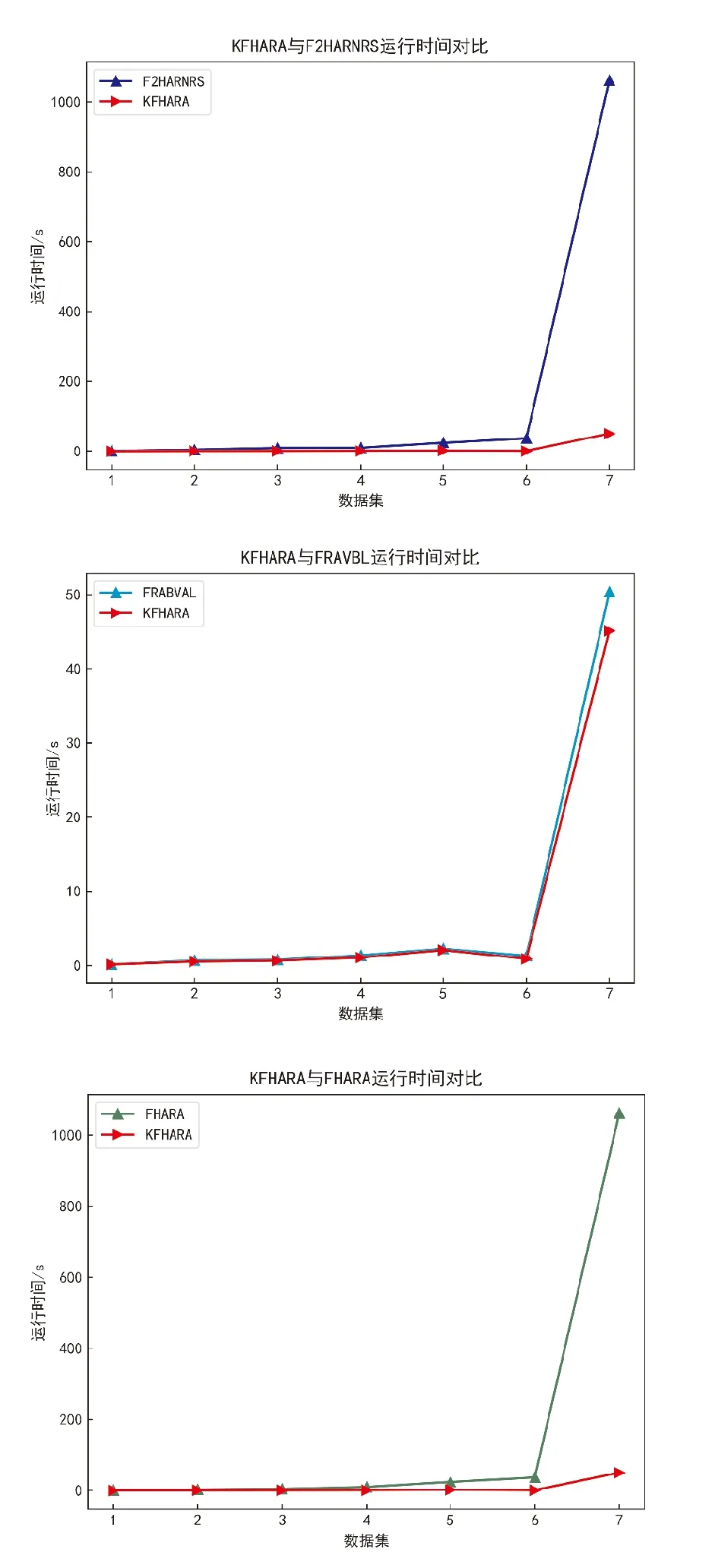
圖3 算法運(yùn)行時(shí)間對(duì)比

隨著原始數(shù)據(jù)集的屬性數(shù)量和樣本數(shù)量逐漸增多,FHARA和F2HARNRS算法耗費(fèi)的時(shí)間越來(lái)越大,當(dāng)數(shù)據(jù)集為高維數(shù)據(jù)時(shí),算法消耗時(shí)間成指數(shù)級(jí)增長(zhǎng),FRABVAL算法因?yàn)槔猛镀笔降膶傩灾匾扰判?算法消耗時(shí)間與前兩種算法相比明顯降低,KFHARA算法的運(yùn)行時(shí)間遠(yuǎn)低于前兩種算法,略低于第3種算法,該算法從處理低維數(shù)據(jù)到處理高維數(shù)據(jù)的運(yùn)行時(shí)間是線性增長(zhǎng)的,面對(duì)高維數(shù)據(jù)時(shí)可以大大降低算法運(yùn)行時(shí)間。如圖3在7個(gè)數(shù)據(jù)集上KFHARA算法運(yùn)行時(shí)間都小于其他算法。

3.2.2 算法約簡(jiǎn)屬性對(duì)比 表3顯示了算法約簡(jiǎn)后所剩屬性個(gè)數(shù)。 整體來(lái)看, 算法都約簡(jiǎn)掉了大量的屬性, 約簡(jiǎn)后的屬性個(gè)數(shù)都小于10， 可見KFHARA算法對(duì)原始數(shù)據(jù)集具有良好的約簡(jiǎn)效果。

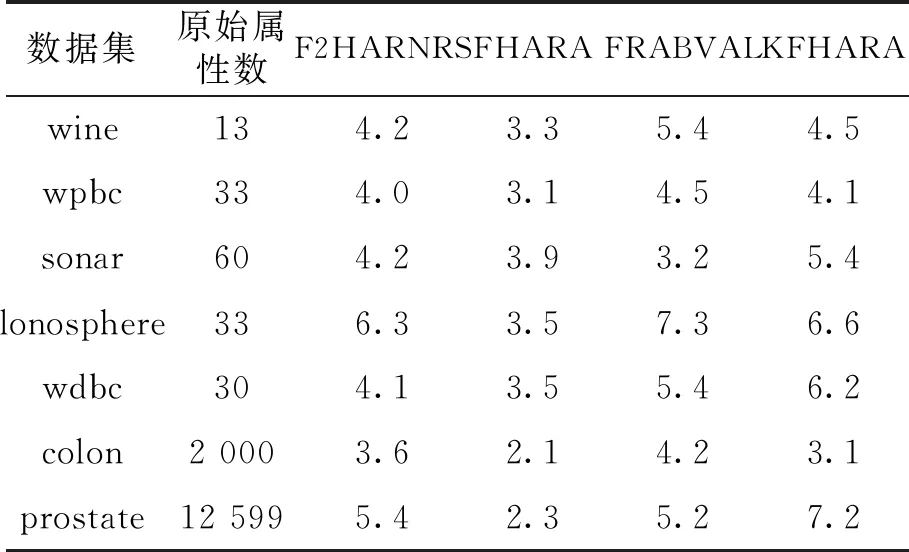
表3 屬性約簡(jiǎn)個(gè)數(shù)比較

3.2.3 分類精度對(duì)比 為得到約簡(jiǎn)集的分類精度,將經(jīng)過(guò)KFHARA等4種算法約簡(jiǎn)后的屬性子集放入不同分類器中做對(duì)比,分別使用KNN,SVM和決策樹分類,得到算法平均分類精度。KNN分類精度表和KNN分類精度圖分別如表4、圖4所示；SVM分類精度表和SVM分類精度圖分別如表5、圖5所示；決策樹分類精度表和決策樹分類精度圖分別如表6、圖6所示。

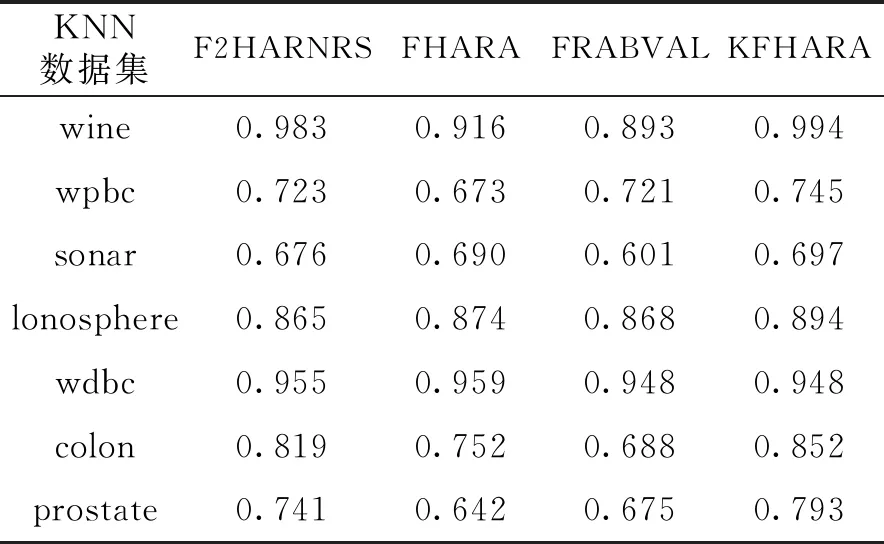
表4 KNN分類精度

表5 SVM分類精度

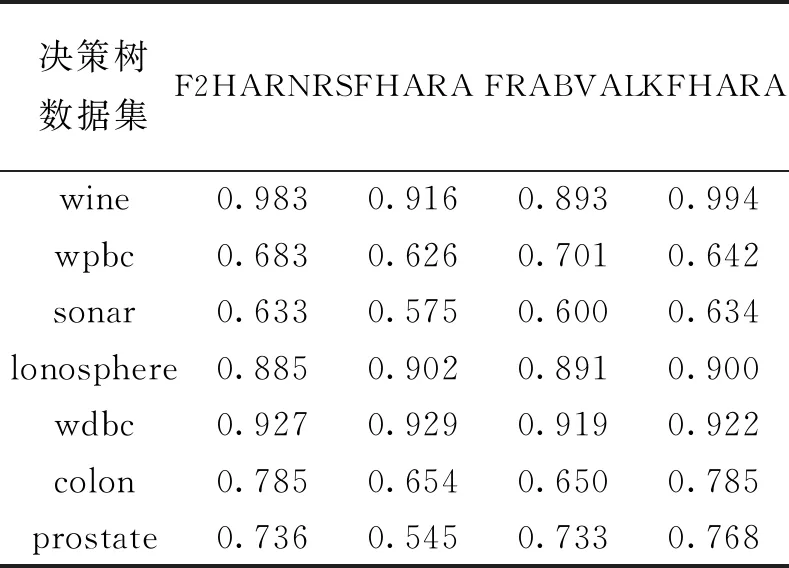
表6 決策樹分類精度

圖4 KNN分類精度

圖5 SVM分類精度

圖6 決策樹分類精度

經(jīng)過(guò)KFHARA算法約簡(jiǎn)后的子集在3種分類器下的7個(gè)數(shù)據(jù)集中進(jìn)行實(shí)驗(yàn)，從運(yùn)行時(shí)間來(lái)看，相較于FHARA和F2HARNRS算法，KFHARA算法的運(yùn)行時(shí)間得到明顯提升， 和同類的針對(duì)屬性重要度的快速屬性約簡(jiǎn)算法FRABVAL相比，運(yùn)行時(shí)間也有所提升。從分類精度上來(lái)看，KFHAR分類精度和其他3種算法相比，略微優(yōu)于精度最高、運(yùn)行時(shí)間最長(zhǎng)的F2HARNRS算法，明顯優(yōu)于其他兩種算法。實(shí)驗(yàn)證明，在保證精度不損失的情況下，KFHARA算法有效地減少了屬性約簡(jiǎn)的時(shí)間，尤其是面對(duì)高維數(shù)據(jù)展現(xiàn)了良好的性能。

4 結(jié)語(yǔ)

為減少冗余屬性對(duì)分類算法運(yùn)行速度和分類精度的影響,本文提出了一種快速屬性約簡(jiǎn)方法KFHARA。該方法通過(guò)改進(jìn)的KNN屬性重要度來(lái)進(jìn)行屬性排序,在不影響精度的情況下通過(guò)減少屬性重要度計(jì)算次數(shù)來(lái)減少算法的運(yùn)行時(shí)間,從而降低時(shí)間復(fù)雜度。本文所提的約簡(jiǎn)算法得到的屬性子集中屬性數(shù)量較多,未來(lái)的研究目標(biāo)是在不影響約簡(jiǎn)速度和分類精度的情況下，逐步減少約簡(jiǎn)子集中屬性的個(gè)數(shù)。