經典-經典變精度概念格的一種屬性約簡

李同軍, 徐珍珍, 吳明瑞, 楊曉平

(1.浙江海洋大學 信息工程學院, 浙江 舟山 316022;2.浙江海洋大學 浙江省海洋大數據挖掘與應用重點實驗室, 浙江 舟山 316022)

德國數學家Wille教授提出的形式概念分析(FCA)理論是用于數據分析和知識處理的一種有效方法,已經被廣泛地應用于數據挖掘、知識工程、信息檢索、軟件工程等許多方面[1-6]。 形式背景是FCA中數據的基本框架,它包括一個對象集、一個屬性集以及兩者之間的一個二元關系。每個形式概念由一個對象子集和一個屬性子集組成,所有形式概念形成一個完備格,即概念格。因此概念格是形式背景中數據知識的一種表現形式,其明確、簡潔的數學結構為其實際應用提供了極大的便利。概念格理論的研究主要集中在概念格構造、規則提取、屬性約簡及應用等方面[7-12]。其中,概念格知識約簡是FCA的一個重要研究方向,主要包括概念約簡、屬性約簡和對象約簡,其中屬性約簡是較為重要的研究領域[13-14]。張文修等在格同構意義下研究了概念格的屬性約簡[15]。

形式模糊背景是經典形式背景在模糊集意義下的一種推廣,其主要特征是經典形式背景中對象集和屬性集之間的二元經典關系變成了二元模糊關系。Burusco和Gonzalez首次將模糊集引入形式概念分析[16]。近年來,在利用模糊邏輯推理和模糊集理論拓展模糊形式概念分析研究方面取得了一定的成果。在剩余格的基礎上,Belohlavek等在形式模糊背景中提出了形式模糊概念格,研究表明提出的模糊概念格具有經典概念格的幾乎所有性質[17-19]。Krajic和Yahia 等獨立地提出了單邊模糊概念格,單邊模糊概念的外延和內涵,一個是經典集,一個是模糊集[9, 20]。Zhang 等提出了變精度概念格,定義了4種類型的變精度概念[21]。在此基礎上,Shao等給出了變精度概念格在減少屬性和減少對象意義下的知識約簡方法,并研究了粒約簡等問題[22-23]。Mao和Miao用圖理論給出了模糊-經典概念格保持交不可約元的屬性約簡方法[24]。Shi和Yang研究了模糊-經典概念格保持屬性粒不變的對象約簡[25]。Lin等定義了布爾矩陣和粒度矩陣,據此給出了一種形式模糊背景的粒度約簡方法[26-27]。

與經典形式背景相比,形式模糊背景的知識約簡研究具有更大的難度。本文針對張文修等提出的變精度概念格[21]提出一種經典-經典變精度概念格的屬性約簡,使得約簡既能簡化形式模糊背景中一類確定性規則的形式表示,又能保持規則的性能不變,同時對屬性約簡的判定、核心屬性的特征刻畫做了研究,最后通過引入辨識屬性的概念,給出一種屬性約簡的方法。

1 預備知識

1.1 伽羅瓦連接和剩余格

(LU,?)是一個偏序集。

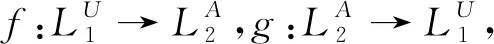
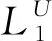
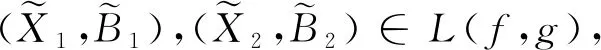
顯然,這里“≤”是L(f,g)上的一個偏序關系。

這時,稱L(f,g)為概念格。

定義3[21]稱L=(L,∧,∨,?,→,0,1)是一個剩余格,如果L滿足以下條件:

1) (L,∧,∨,0,1)是具有最小元素0和最大元素1的格；

2) (L,?,1)是交換幺半群；

3) (?,→)是L中的伴隨對,

即

a≤(b→c)?a?b≤c。

剩余格(L,∧,∨,?,→,0,1)中的算子→稱為剩余蘊涵,它滿足下列基本性質[29]:a,b,c∈L,{ai,i∈J}?L,{bj,j∈J}?L,

(L1) 二元運算?關于兩個變量都是單調遞增的;

(L2) 剩余蘊涵→關于左變量單調遞減,關于右變量單調遞增;

(L3)b→c=∨{a∈L|a?b≤c};

(L4) 1→a=a,a→b≥b;

(L5)a→b=1?a≤b;

(L6) (a?b)→c=a→(b→c)=b→(a→c);

(L9)a?(a→b)≤b,b≤a→(a?b),

a≤(a→b)→b。

在下文,假設剩余格為

L*=([0,1],∧,∨,?,→,0,1),

即其支撐集為[0,1]。

L*中常見的伴隨對(?,→)有以下幾種[28]:

1) (Lukasiewicz結構)

a?b=max{a+b-1,0},

a→b=min{1-a+b,1};

2) (Godel結構)

3) (乘積結構)

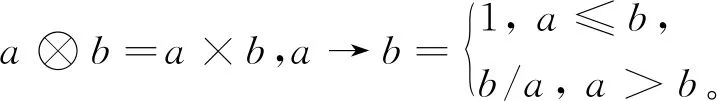
1.2 變精度概念格

由剩余格L*上剩余蘊涵→的性質(L4)可知

(1)

(2)

從式(1)和式(2)可以看出,定義5中的兩個算子*δ與剩余蘊涵算子→的類型無關,也就是說,用不同類型的剩余蘊涵定義的X*δ和B*δ是分別相等的,而且容易驗證下面性質成立。

2)X?X*δ*δ,B?B*δ*δ;

3)X*δ=X*δ*δ*δ,B*δ=B*δ*δ*δ;

5)X?B*δ?B?X*δ。

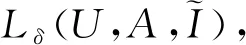
X*={a∈A|X?Ia}，X?U,

B*={x∈U|B?xI}，B?A。

其中,

xI={a∈A|(x,a)∈I},x∈U,

Ia={x∈U|(x,a)∈I},a∈A。

記(U,A,I)中所有概念組成的集合為L(U,A,I),或L(I)。記L(I)中所有概念外延構成的集合為Ext(U,A,I),或簡記為Ext(I)。

(3)

對于B?A,容易驗證

(4)

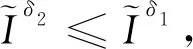
X*δ2?X*δ1,B*δ2?B*δ1。

證明只證一個不等式,另一不等式同理可證。下面只證X*δ2?X*δ1。

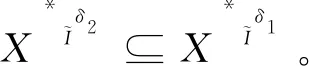
U={x1,x2,x3,x4},A={a,b,c,d,e},

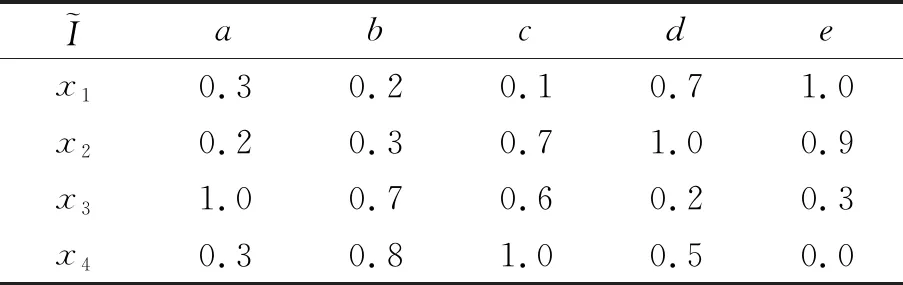
表1 一個形式模糊背景

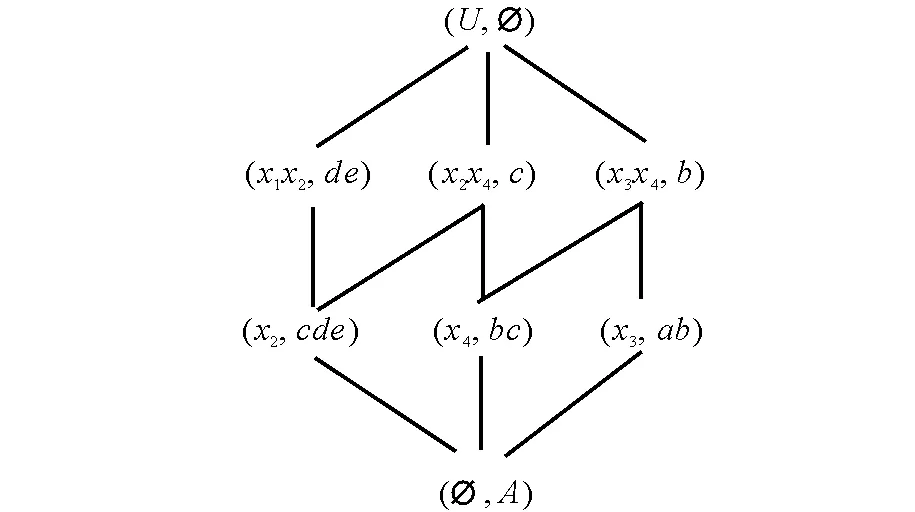
圖 1 例1中的概念格

圖2 例1中的概念格

2 規則提取與屬性約簡的定義

2.1 規則提取

其含義可解釋為:對于x∈X,當且僅當x具有屬性ai1,…,aik的程度都不低于δ。

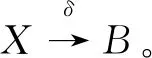
(5)

2.2 屬性約簡的定義

對于一個經典形式背景(U,A,I),C?A,記IC=I∩(U×C),則稱形式背景(U,C,IC)為(U,A,I)的子背景。記(U,C,IC)上的兩個*算子為*C。

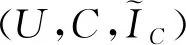
(6)

(7)

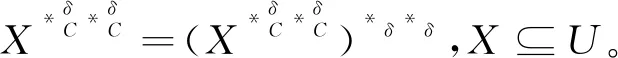
由命題5可得下面結論。

推論1設(U,A,I)是一個形式背景,若C?A,則對于X?U,都有X*C*C∈Ext(I)。

命題5和推論1說明,形式模糊背景和經典形式背景的子背景的概念的外延仍然是原背景中概念的外延。

表2 例3中的形式模糊子背景

圖3 例3中的概念格

證明由式(3)可知只需證明,

對于X?U,有

故

3 屬性約簡

3.1 屬性約簡的判定

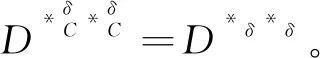
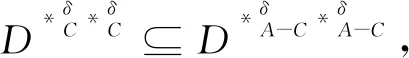
故C為關于D的δ0-協調集。

3.2 屬性約簡的方法

DS((X,B)δ)=D*δ-B,

稱DS((X,B)δ)為(X,B)關于D的δ0-辨識屬性集,簡稱辨識屬性集。

表3 精度δ≥0.3的辨識屬性集

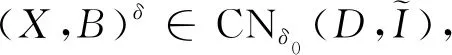
(D*δ∩C)-(B∩C)=C∩(D*δ-B)=

C∩DS((X,B)δ)≠?。

DS((X,B))={a}。

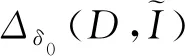
利用定理4不難證明下面結論成立。

∨(∧Ck)

則屬性集C1,C2,…,Ck是關于D的全部約簡。

∧(d∨e)∧e∧e∧e

利用邏輯運算的吸收律、分配律和交換律將上式恒等變形,可得

a∧d∧e,

故由定理6可知,精度0.3下關于D的約簡只有一個, 即{a,d,e}。

4 結語

經典-經典變精度概念格是一種類型的變精度概念格,雖然經典-經典變精度概念在形式上與經典形式概念完全一樣,但是它們卻是來自于對象和屬性間的模糊關系,不同閾值對應不同的經典形式概念。正是由于經典-經典變精度概念的外延和內涵都是經典集合,所以經典-經典變精度概念格在實際應用中更具優勢。因此研究基于經典-經典變精度概念格的形式模糊背景的屬性約簡具有明顯的理論意義和實際應用價值。本文研究了經典-經典變精度概念格的一種屬性約簡問題。提出了一種保持確定性規則的后件的語義不變的屬性約簡概念,研究了屬性協調集的判定,給出了核心屬性的特征刻畫。基于粗糙集理論中辨識矩陣方法,構造了經典-經典概念的辨識屬性集,進而定義了辨識函數,證明了依據辨識函數可以獲得全部約簡。同時結合示例解釋了一些主要概念、結論和方法。