淺論數學“解題模型”教學四步驟
——以“十字架”模型為例

324400 浙江省龍游縣教育局教研室 徐偉建

324402 浙江省龍游縣小南海初中 余 昊

數學“解題模型”通常是指教師在解題教學中發現并總結出的一些結論性認識，它表現為一種能有效解決某類題型的技巧，是課標、教材中知識的進一步拓展、延伸或更加直觀的表述[1].數學“解題模型”往往是學生解題時聯想的“原型”，是探究問題的固著點，它能夠啟迪解題方向，幫助學生形成良好的解題直覺，并實現解題經驗和方法的有效遷移.因此，在日常教學中，以“解題模型”的運用進行專題復習教學深受教師青睞.然而，筆者發現，“解題模型”教學中還存在著許多不足之處.例如，有的教學“掐頭去尾”，采用“模型+練習”的方式，缺少模型提煉與深度拓展的過程，不知模型從何而來，到何處去；有的模型呈現割裂單一，缺少系統架構；有的模型運用機械重復，問題設計缺少層次感；還有的教學在模型運用之后，缺乏思想方法的提煉滲透等.種種數學“解題模型”教學的誤區，使教學陷入“應試教育”的泥淖.

那么，如何開展數學“解題模型”教學呢？筆者以“十字架”模型的教學設計為例，探討“解題模型”教學的四個步驟.

一、 模型提煉

數學“解題模型”是抽象的，而數學抽象需要學生經歷觀察、比較、分析、概括等數學學習活動.數學概念的抽象需要經歷上述過程，數學“解題模型”的形成也是如此.“解題模型”的提煉過程，就是探尋模型出處，促進學生認知模型結構的過程.

圖1

問題1已知：如圖1，在正方形ABCD中，若E，F分別是BC，CD上的點，AE⊥BF.求證：AE=BF.

問題1為浙教版教材八年級下冊“5.3正方形(2)”中的習題(P.127第4題).將問題1中的線段AE，BF位置進行適當平移，可得到如下問題2、問題3.

問題2已知：如圖2，在正方形ABCD中，若E，F，G分別是BC，CD，AB上的點，AE⊥GF.求證：AE=GF.

問題3已知：如圖3，在正方形ABCD中，若E，F，G，H分別是BC，CD，AB，AD上的點，HE⊥GF.求證：HE=GF.

圖2圖3

解析：對于問題1，可以直接判定Rt△ABE≌Rt△BCF，證得AE=BF.對于問題2，添加一條輔助線，構造Rt△GMF(如圖4所示)，則Rt△ABE≌Rt△GMF,結論得證，也可以平移GF，將問題化歸到圖1解決.對于問題3，添加兩條輔助線，構造Rt△HNE和Rt△GMF(如圖5所示)，則Rt△HNE≌Rt△GMF,結論得證，也可以平移GF，HE，將問題化歸到圖1解決.

設計意圖：問題1源自教材習題，問題2、問題3是問題1的變式.以教材習題及其變式題創設問題情境，有兩方面的意義：一是讓學生體會到“解題模型”根植于教材，探尋到模型的出處；二是為學生提供足夠數量的感知材料，便于學生從中發現并提煉出“解題模型”.

圖4圖5

完成解題后，引導學生思考下列問題.

思考題1觀察圖1-圖3，除了正方形之外，它們都有一個怎樣的模型結構？

思考題2該模型需要具備的條件是什么？結論又是什么？

思考題3證明結論的方法是什么？

設計意圖：設計三道思考題，重在讓學生經歷模型的提煉過程.思考題1引導學生在觀察、比較、分析圖1-圖3的基礎上,形象地感知解題模型——“十字架”模型.思考題2引導學生尋找模型具備的條件，即兩條線段互相垂直，且垂線段的端點分別在正方形的兩組對邊上；結論是這兩條垂線段相等.思考題3證明結論的方法是借助正方形的邊和角構造出全等的直角三角形，再運用全等三角形性質得到.通過以上問題的探究，促進學生加深對模型結構的認知，為模型的遷移運用奠定基礎.

典型的“解題模型”通常來源于教材，它是教材知識的拓展延伸.為此，情境問題應源自教材中的例題、習題，這能讓學生體會到模型存在的重要基礎，引導學生關注教材.模型提煉還應在預設或生成問題的啟發引導下，讓學生自主探究，發現、提煉模型，辨析模型條件，獲得模型結論，掌握證明結論的原理或方法，這些都是模型運用與拓展的前提.因此，“解題模型”教學不能忽視模型的提煉過程.

二、 模型演變

在“解題模型”教學中，應該系統地、聯系地看待“解題模型”.在進行教學設計時，應進行如下思考：還有沒有其他模型可通過該模型演變得到？它們之間存在怎樣的聯系？變式模型是否也存在著廣泛的運用？經過深入思考，系統地梳理模型及其變式，讓學生從整體上架構起模型體系.例如，通過梳理發現，除了運用于正方形背景中，“十字架”模型在矩形背景中同樣有著廣泛運用，自然就得到如下的演變模型.

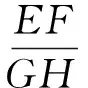
圖6圖7

思考：請你比較矩形和正方形背景中“十字架”模型的條件、結論和證明結論的方法，它們有何區別與聯系？

設計意圖：問題4使模型的背景由正方形變成了矩形.通過解題后的思考，學生進一步明確在矩形背景中，該模型的條件是兩條線段互相垂直(即EF⊥GH)，且垂線段的端點分別在矩形的兩組對邊上；結論是這兩條垂線段與矩形的邊長對應成比例；解題的基本方法是借助矩形的邊和角構造出相似直角三角形，再運用相似三角形性質解題.

三、 模型運用

心理學研究表明，數學模型在獲得后若不能得到及時鞏固與內化就會被遺忘，因此，運用、鞏固模型是十分重要的環節.模型的運用應遵循知識發生、發展的邏輯鏈條，由淺入深、層層遞進設計.通過模型運用環節，促進學生識別模型，運用模型的基本結論和方法解決新問題，達到學習經驗有效遷移的功效.

問題5已知：如圖8，在正方形ABCD中，若E，F分別是BC，AB上的點，且CF⊥DE，過點E作EG⊥DE，使得EG=DE，聯結FG.試判斷FG與CE的數量關系和位置關系，并說明理由.

圖8

解析：FG∥CE，FG=CE.

理由：根據正方形中的“十字架”模型，可得DE=CF，因為EG=DE，DE=CF，所以EG=CF;因為EG⊥DE,CF⊥DE，所以EG∥CF.因此，四邊形ECFG是平行四邊形，得到FG∥CE，FG=CE.

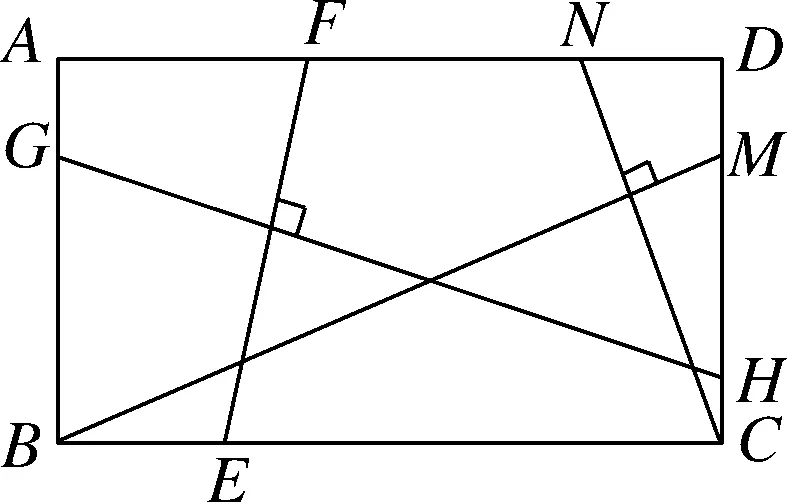
圖9

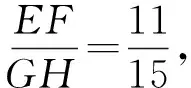
設計意圖：問題5有一定的綜合性，學生既要識別正方形背景中的“十字架”模型，運用其結論和方法，也要結合平行四邊形判定與性質解決問題.問題6在矩形背景中增加模型個數，圖形看似復雜，但若能識別模型，并兩次運用模型結論，再進行適當轉化，問題不難解決.問題5、問題6將完整的“十字架”模型置于較復雜的圖形中，增強學生識別、運用模型的能力.

四、 模型拓展

數學“解題模型”的運用不僅局限于模型的直接運用，還需要適度拓展，通過模型拓展運用，拓寬學生視野，發展學生思維，滲透化歸等數學思想方法.模型的拓展運用，通常可采用“虛化”模型結構或者“弱化”模型背景等策略，化“全模”為“半模”，引導學生以模型為固著點，展開積極的聯想，找到解題方向，使問題化生為熟、化難為易，從而達到從運用模型向構建模型的跨越.

問題7如圖10，將邊長為4的正方形ABCD折疊，使得點A落在CD的中點E處，折痕為FG，點F在AD邊上，求折痕FG的長度.

圖10圖11

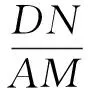
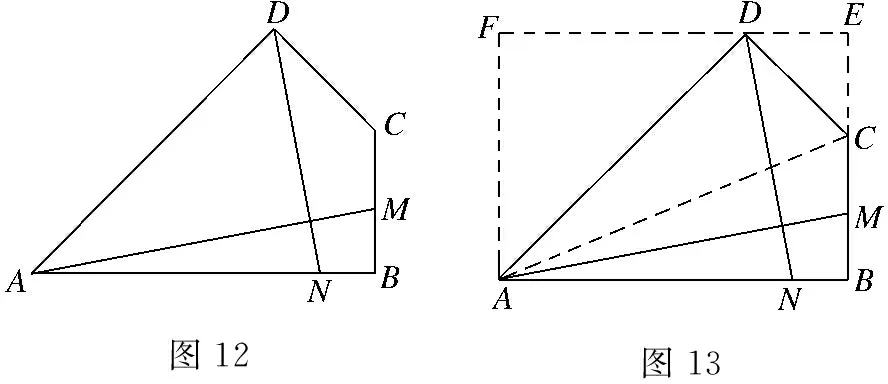
圖12圖13

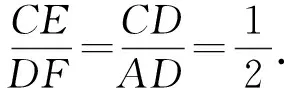
設計意圖：對于問題7，直接求出折痕FG的長度比較繁瑣，通過觀察可以發現，線段GF的兩個端點在正方形的一組對邊BC，AD上，如果另外有一條線段的兩個端點在另一組對邊上，且與GF垂直，就可以利用“十字架”模型解決問題，這就為解題提供了聯想的方向.依據圖形折疊性質，聯結對稱點A，E，隱藏的“十字架”模型即浮出水面(如圖11所示)，問題迎刃而解.問題8雖然具有完整的“十字架”(AM⊥DN)，但垂線段AM，DN的端點并不滿足在矩形的兩組對邊上，觀察圖形特點，借助∠ABC=90°，通過添加輔助線構造出矩形背景(如圖13所示)，此時，頓有一種豁然開朗的感覺.對于模型的拓展運用不能停留在解決問題的層面，還需要適時反思，感悟其中的數學思想方法.例如，解題后引導學生再思考以下問題：你為什么會聯想到“十字架”模型？你是怎樣轉化到“十字架”模型的？在轉化的過程中，你運用了什么數學思想方法？在反思感悟的過程中，學生自然能深刻感受到化歸、類比等數學思想方法的神奇力量，也實現了知識與經驗的有效遷移.

“解題模型”的拓展運用關鍵在于問題的設計，問題既要有層次性，避免機械重復地講解與練習，也要有適切性.問題并非越難越好，好的拓展題應讓學生從題意中聯想到“解題模型”，啟迪解題方向，形成解題思路，讓學生體會到“山重水復疑無路，柳暗花明又一村”的成就感和愉悅感.這樣的拓展運用既能起到固本的功效，讓學生體驗到模型學習的意義，又能幫助學生積累聯想經驗，提高解題能力，發展學生思維水平.

五、結語

數學“解題模型”的教學要讓學生經歷“模型提煉、演變、運用、拓展”這一完整的學習過程，在過程中讓學生探尋模型出處，認知模型結構，架構模型體系，實現從識別模型到構建模型的提升；“解題模型”教學既要注重模型基本結論的運用，也要注重數學思想方法的提煉與滲透，這樣才能發揮“解題模型”教學的更大價值.