一般線性黏彈性阻尼器保護系統非均勻與完全非平穩地震響應解析分析

李創第 王博文 昌明靜

摘要：為建立設置支撐的一般線性黏彈性耗能結構阻尼器保護系統的抗震設計和動力可靠度分析方法，提出了在非擴階空間上，基于非均勻和完全非平穩地震激勵下，設置支撐的一般線性黏彈性耗能結構阻尼器保護系統響應的通用解析解。采用設置支撐黏彈性阻尼器的最一般積分型分析模型，用微分積分方程組實現設置支撐的一般線性黏彈性阻尼耗能結構系統的非擴階建模；采用傳遞矩陣法，直接獲得耗能結構阻尼器保護系統在任意激勵和非零初始條件下瞬態響應的非擴階模態疊加解析解；應用此解析解和隨機振動頻域分析法，獲得了耗能結構阻尼器保護系統在一般和8種經典均勻與非均勻非平穩地震激勵以及完全非平穩地震功率譜模型下的具體響應解析解。通過減震和隔震兩種典型結構的復模態法和頻響函數法的理論驗證分析，以及均勻、非均勻、完全非平穩算例響應分析，證明了本文方法的正確性、簡易性和普適性；所獲得的瞬態響應解析解和非平穩地震響應分析法，一方面可對整體耗能系統各構件進行基于泊松假設的抗震動力可靠度分析，另一方面將為結構系統建立基于反應譜的模態疊加抗震設計提供分析路徑。

關鍵詞：耗能結構系統；黏彈性阻尼器；瞬態響應；非均勻與完全非平穩響應；解析解

中圖分類號： TU311.3??? 文獻標志碼： A??? 文章編號：1004-4523（2022）05-1084-17

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.006

引言

目前國內外最為成熟的提高結構抗震抗風能力的被動控制技術有耗能減震和橡膠基礎隔震[1?2]。耗能結構是通過設置阻尼器保護系統（阻尼裝置和支撐構件）[1?7]以達到很好的耗能效果。支撐剛度不僅影響結構的整體響應[8?12]，而且影響阻尼器的受力和變形。阻尼器保護系統的破壞加重了結構的損傷甚至倒塌[13]，因此中國相關規范[1，14]明確要求阻尼器保護系統應具有足夠的抗震能力，故對阻尼器保護系統的研究具有工程意義。

黏彈性阻尼器是一種有效的被動控制裝置，具有廣泛的工程適應性[3]。目前的研究方法無法將黏彈性耗能結構阻尼器保護系統的響應精確分解為各模態響應的線性組合，導致其精確的抗震反應譜設計法無法建立，因此黏彈性減振控制的實用設計理論及其在規范中的應用已被列為中國土木結構振動控制領域的關鍵問題之一[15]。

黏彈性耗能結構系統現有解析法的代表有擴階精確法[16?17]、非擴階近似法[18]等，它們存在物理意義不明確、假設較多、計算效率低等[19?20]缺陷導致適用性受限。非擴階精確法[21]求解過程簡單，計算效率高，獲得的黏彈性耗能結構響應解析解物理意義明確，從本質上精確揭示了黏彈性耗能結構保護系統的振動機理，避免了結構運動方程模態無法解耦的問題[21]。該方法對不同黏彈性阻尼器耗能結構具有簡易性和普適性。

關于一般黏彈性阻尼器響應分析的重要性早已形成共識[11?12，22?24]，但目前僅獲得單自由度一般黏彈性耗能結構在簡諧荷載激勵下穩態響應的解析解，尚未獲得多自由度設置支撐的一般黏彈性耗能結構阻尼器保護系統在任意荷載激勵下瞬態響應的非正交模態疊加精確解析解。

地震的整個過程，一般是非平穩隨機過程[25]。一般用 Priestley 提出的演變譜模型來分析非均勻非平穩地震響應[26]。平穩地震激勵模型主要有白噪聲模型[27]、Kanai Tajimi譜?[28]、Clough Penzien譜?[29]、胡聿賢譜[30]等，其中 Kanai ?Tajimi譜地震激勵模型符合地震動特點且表達式相對簡單，受到廣大科研人員的關注[31?32]。 Conte 等[33]提出了可以由實際地震加速度演變功率譜經自適應最小二乘法擬合確定參數的完全非平穩模型，該模型同時反映了地震的強度非平穩和頻率非平穩特性，其計算參數可通過實際地震加速度演變功率譜擬合得到，具有較強通用性。

關于一般黏彈性耗能結構的非平穩響應分析，目前已獲得廣義 Maxwell 阻尼耗能結構在平穩濾過白噪聲激勵下的平穩響應解析解[34?36]和 Maxwell 阻尼耗能結構均勻非平穩地震響應解析解[20]，然而對于多自由度設置支撐的一般黏彈性耗能結構阻尼器保護系統在一般和多種[37]均勻與非均勻非平穩激勵以及完全非平穩地震功率譜模型下的響應解析分析尚未建立。

本文采用設置支撐黏彈性阻尼器的最一般積分型分析模型，將傳遞矩陣法應用到一般黏彈性阻尼耗能結構系統中，求解過程簡單，計算效率高，在獲得了黏彈性耗能結構阻尼器保護系統在任意激勵作用下瞬態響應非擴階模態疊加精確解的基礎上，建立了一般線性黏彈性耗能結構阻尼器保護系統的均勻與非均勻以及完全非平穩地震響應解析分析。采用減震和隔震兩種典型結構的復模態法和頻響函數法的理論驗證分析，以及均勻、非均勻、完全非平穩算例響應分析，證明了本文方法的正確性、簡易性和普適性。一方面可對整體耗能系統各構件進行基于泊松假設的抗震動力可靠度分析；另一方面將為結構系統建立基于反應譜的模態疊加抗震設計提供分析路徑。

1 結構運動方程

設置支撐的一般線性黏彈性阻尼器的 n 個自由度結構系統的運動方程可表示為：

式中 M 為結構的質量矩陣；C 為結構的黏滯阻尼矩陣；K 為結構的剛度矩陣；x 為結構位移向量；pGi （ t ）和 Li 表示等效后第i個阻尼器的作用力及其影響向量，m 為阻尼器總數；F （ t ）為任意外載向量；對于地震激勵 F（ t ）=- r g （ t ）， g （ t ）為地面地震加速度，r 為常數向量。

等效后黏彈性阻尼器受力pGi （ t ）的一般積分型本構方程為：

式中kGi和hGi （ t ）分別為等效后第i個阻尼器的平衡剛度和松弛函數，i =1，2，…，m；原阻尼器pQi （ t ）及其支撐剛度kbi與等效阻尼器pGi （ t ）之間的轉換關系詳見文獻[38]。

故設置支撐的一般線性黏彈性阻尼耗能結構系統的運動方程可表示為：

式中 KG 和hG （ t ）分別為等效后阻尼器體系的對稱平衡模量和松弛函數矩陣。

2 結構系統的傳遞矩陣法

2.1? 阻尼器的傳遞矩陣法

設結構的初始條件為：

由拉氏變換，式（3）可轉化為：

式中 xˉ （ s ），Fˉ （ s ），h ˉ G （ s ） 分別為 x （ t ），F （ t ），h G （ t ）的拉氏變換；s 為拉氏變換的狀態變量；D （ s ）和 H（ s ）分別為結構的阻抗和傳遞矩陣。

結構的特征值方程為：

方程（2）可表示為：

對式（10）和（11）取拉氏變換，并考慮關系式（6），可得：

式中?? Gi （ s ）和（ s ）分別為pGi （ t ）和 g （ t ）的拉氏變換。

故阻尼器的變換向量 g （ t ）的傳遞矩陣 Hg （ s ）和阻抗矩陣 Dg （ s ）分別為：

由阻尼器pGi （ t ）的實際物理意義和其本構關系式（2）可知：pGi （ t ）≠0；故：

由式（17）對任意初始位移 x0均成立得：

故阻尼器的變換向量 g （ t ）的特征值方程為：

由式（18）和（19）可知：g （ t ）的特征值與結構位移 x （ t ）的特征值完全相同。x （ t ）的每個特征值sj對應的右、左特征向量uj和uj（T），g （ t ）的每個特征值sj對應的右、左特征向量ugj和 u gj（T），它們滿足的方程分別為：

其中，j =1～M，M 為特征值個數。

由式（20）～（22），可得 g （ t ）與 x （ t ）的特征向量的對應關系為：

根據前期研究，對于 g （ t ）的傳遞矩陣 Hg （ s ）和sHg （ s ），下列解析式均成立[21]：

式中sj為 g （ t ）的阻抗矩陣 Dg （ s ）的特征值，其值與結構位移 x （ t ）的阻抗矩陣 D（ s ）的特征值完全相同；ugj為動剛矩陣 Dg （ s ）對應于特征值sj的特征向量。由式（14）～（16），可得：

將式（27）代入式（26），可得：

將式（23）代入式（28），可得：

由于uj是 D（ s ）對應于特征值sj的特征向量，故D （ sj ） uj =0，代入式（29）可化簡為：

式中：

2.2 阻尼器受力瞬態響應解析解

由式（12），（14），（33）和式（8），可得：

由拉氏逆變換，式（35）可轉化為：

式中δ（ t ）為 Dirac delta 函數。

對于 t >0，阻尼器受力的瞬態響應解析解為：

式中aj （ t ）表示初始條件產生的響應，表達式為：

對于零初始條件，

同理，由式（12），（14），（34）和式（8），可得阻尼

器受力速度的瞬態響應解析解為：

2.3 結構瞬態響應解析解

同理可得結構的位移和速度的瞬態響應解析解為：

其中aj （ t ）如式（38）所示。

若在初始條件為零的情況下，則aj （ t ）=0（ j =1～M ）。

2.4 支撐和阻尼器瞬態響應解析解

支撐剛度、原阻尼器和等效阻尼器之間滿足以下關系：

式中xbi，xQi和 x Δi分別為支撐位移、原阻尼器位移和層間相對位移；kbi為支撐剛度。

對于 t >0，由式（42）可得：

將式（37），（39）～（41）分別代入式（43）和（44），可得：

2.5 結構系統地震響應

零初始條件下，由式（40），（41），（37），（39）和式（45）～（48）可得一般黏彈性阻尼器 n 個自由度耗能結構的位移、速度，阻尼器受力、受力速率，支撐位移、速度，阻尼器位移、速度響應解析式可統一表示為：

式中? l=1～8；S1（ t ）為結構的位移響應，S2（ t ）為結構的速度響應，S3（ t ）為阻尼器受力響應，S4（ t ）為阻尼器受力速率響應，S5（ t ）為支撐位移響應，S6（ t ）為支撐速度響應，S7（ t ）為阻尼器位移響應，S8（ t ）為阻尼器速度響應；ρlj為響應系數；ηj 為計算常數。響應系數分別為：

ρ8j = sjηj {1- k bi（-）1[ kGi + sj? Gi （ sj ）]} L i（T）ujuj（T） r （57） bj （ t ）為標準一階系統對地震激勵的響應，即：

3 結構系統非平穩響應一般解析式

3.1 非平穩地震激勵模型

地震動過程通常包含兩個非平穩過程：強度非平穩和頻率非平穩，通常采用 Priestley 提出的演變功率譜模型，它可以表示為：

式中i =；“*”表示取共軛項；a （ω，t ）是 t 與ω的確定性調制函數，滿足 a （ω，t ）= a?（-ω，t ）；N（ω）是一個正交增量過程；δ（?）為 Dirac delta 函數；S f （ω）為功率譜密度函數。

g （ t ）的協方差函數可表示為：

特別是當 t1= t2時，

3.2 結構系統非平穩響應的一般解析式

結構系統一般響應 S（ t ）的非平穩協方差函數的表達式為：

將式（62）代入式（65）可寫成：

式（67）為標準一階系統在激勵eiωt a （ω，t ）下的響應積分形式。因此，式（67）可表示為如下方程的解：Y?j （ω，t ）= sjYj （ω，t ）+ eiωt a （ω，t ），

式中Yh，j （ω，t ）為式（68）的齊次解，Yp，j （ω，t ）為式（68）的特解。

?由初始狀態 t =0所決定。假定特解Yp，j （ω，t ）已經求出。

由式（66）和（67）可得：

由式（69）～（71）可得：

工程上廣泛應用的調制函數為下式的線性組合[19]：

式中? r 為整數；ε（ω）和α（ω）為描述調制函數的參數。

因此，式（72）中的特解為：

將式（74）代入式（72）得耗能結構系統非平穩響應的一般解析式為：

4 幾種經典調制情況下非平穩響應具體解析式

4.1 Shinozuka-Sato 型調制函數

式中ε=? e? ln（）；α1，α2為已知常數。

式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（77）代入式（72）得：

4.2 Hsu-Bernard 型調制函數

式中ε=αe，α為已知常數。

式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（80）代入式（72）得：

4.3 Goto-Toki 型調制函數

式中 A 0，tp為已知常數。

式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（83）代入式（72）得：

Iyengar 型調制函數

c，d，α為已知常數。

式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（86）代入式（72）得：

4.5? 分段型調制函數

式中 A 0，c，t1，t2為已知常數。

當0≤ t ≤ t1時，式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定的。Yp，j 可表示為：

將式（89）代入式（72）得：

當 t1≤ t ≤ t2時，式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（91）代入式（72）得：

當 t ≥ t2時，式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（93）代入式（72）得：

4.6? 余弦型調制函數

式中? c，d，θ為已知常數；c ≥ d。

式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（96）代入式（72）得：

4.7? 正弦型調制函數

式中? c，d，θ為已知常數；c ≥ d。

式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（99）代入式（72）得：

4.8 Spanos-Solomos型調制函數

式中ε（ω），α（ω）表示以ω為自變量的函數。

式（70）中?由初始狀態 t =0時，Yj （ω，0）=0所決定。Yp，j 可表示為：

將式（102）代入式（72）得：

5 完全非平穩功率譜模型

完全非平穩模型[33]的演變功率譜密度函數為：

U （ t - tf ）為單位階躍函數，

式中? S f （ω）為第f個平穩高斯過程的功率譜密度函數；af （ t ）為第f個高斯過程的調制函數；vf和ηf 分別為隨機過程的頻帶寬和卓越頻率；εf，tf，rf，αf 為描述調制函數af （ t ）的4個參數。

式（70）中?由初始狀態 t = tf時所決定。由式（68）～（72），同理可得：

式中Yj，f （ω，t ）和Yp，j （ f ）（ω，t ）分別是在 p 個相互獨立的、零均值的、均勻調制高斯激勵下，式（68）的第f個通解和特解。

由式（68）～（74）可得式（108）的特解為：

將式（109）代入式（108）得：

將式（111）代入式（66）得：

6 驗證和算例分析

下面通過兩種一般多自由度典型耗能結構的驗證分析和算例分析證明本文方法的正確性。

6.1 多自由度 Maxwell 阻尼減震系統

6.1.1 運動方程

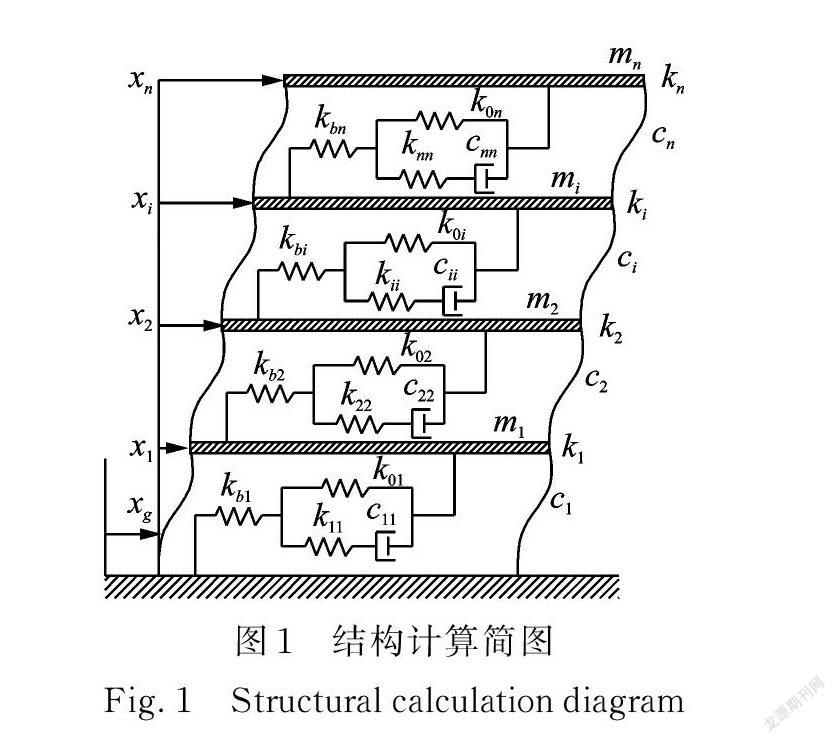
設 n 層結構的質量矩陣為 M；結構的剛度矩陣為 K；結構的黏滯阻尼矩陣為C；層間質量、剛度和阻尼分別為 mi，ki，ci，（ i =1，2，…，n ）；kbi，k0i 分別為層間設置的支撐剛度和 Maxwell 阻尼器 pi （ t ）的平衡模量；層間的 Maxwell 阻尼器的剛度為kii；阻尼器的阻尼為? cii；阻尼器的松弛參量為μ ii（ i =1，2，…，n ）；x 為結構相對于地面的位移向量。在地震動 g （ t ）作用下，結構計算簡圖如圖1所示，結構運動方程為：

hQi （ t ）為原結構第i個阻尼器的松弛函數；kGi和hGi （ t ）分別為等效后第i個阻尼器的平衡剛度和松弛函數，i =1，2，…，n 。 Qi （ s ）， Gi （ s ）分別為hQi （ t ），hGi （ t ）的拉氏變換。

其中：

將式（114）代入式（113），結構運動方程可化為：

由拉氏逆變換，式（116）可轉化為：

6.1.2 驗證分析本文方法

結構特征值sj及其對應的特征向量uj的方程為：

由此求得原始結構3n個特征值sj及其對應的非零特征向量uj （ j =1～3n ）。

由式（31）得：

由式（40），（41），（37），（39）和式（44）～（48）在零初始條件下，結構的位移、速度，阻尼器受力、受力速率，支撐位移、速度，阻尼器位移、速度響應為：

復模態法

（1）結構狀態方程

令：v （ t ）= x? （ t ），那么，結構運動方程（113），（114）可表示為擴階形式：

式中：

式中? I 為 n 階單位矩陣。

（2）結構特征值和特征向量分析

令：

則結構的右、左模態方程為：

將式（145）代入式（143），經化簡得：

將式（146）代入式（144），經化簡得：

對比式（128）和式（148），（151）得，復模態法與本文方法得到的特征值完全相同，且復模態法得到的特征向量可用原結構的特征向量表示。

由式（130），（140），（145）和（146），易得：

（3）結構系統響應分析

零初始條件下，結合復模態理論可得：

結構的位移、速度，阻尼器受力、受力速率，支撐位移、速度，阻尼器位移、速度響應為：

對比式（130）～（137）和式（155）～（162）得，兩種方法所得的結構系統響應解析式完全一樣，從而驗證了本文方法的正確性。

6.2 多層耗能隔震結構

6.2.1 運動方程

設多層結構的質量矩陣為 m0；結構的剛度矩陣為 k0；結構的阻尼矩陣為 c0；層間質量、剛度、阻尼分別為 m0i，k0i，c0i （ i =1～n ）；隔震層的質量、剛度和阻尼分別為 m，k，c 。隔震層設置帶支撐的一般線性黏彈性阻尼器的阻尼力為 PG （ t ），其松弛函數和平衡剛度分別為hQ （ t ）和 k0，水平支撐剛度為 kb 。上部結構與隔震層的相對位移向量為 x0，隔震層與地面的相對位移為 x，在地震動 g （ t ）的作用下，該耗能隔震結構的計算簡圖如圖2所示，運動方程為：

M0= m + m0i；1為單位列向量；hG （ t ）和kG分別為等效阻尼器的松弛函數和平衡剛度：

式中?? Q （ s ）為松弛函數hQ （ t ）的拉氏變換； G （ s ）為松弛函數hG （ t ）的拉氏變換。

將位移向量 x0按上部結構第一振型展開得：

則式（163）～（165）可化為對稱微分積分方程：

式中

耗能隔震結構系統上部結構第一振型φ1對應的廣義質量為 M1；振型參與系數為 r1；阻尼比為ξ1；頻率為ω1。

6.2.2 驗證分析算例

在零初始條件下，由式（40）和（37）可得結構系統的脈沖和頻率響應函數分別為：

式中i表示某一層，所以當表示具體某一層即隔震層的時候可以省略i，LT =[0? 1]。

由式（169）和（165）直接獲得的頻率響應函數為：

式中? G （ iω）是hG （ t ）的傅氏變換。

由于式（177）～（180）均為解析解，所以應該相等。

某6層基礎隔震鋼筋混凝土框架結構，結構各層質量 m01～m02為300×103 kg，m03～m06為270×103 kg；層間剛度 k01～k02為4×105? kN m，k03～k06 為3.6×105? kN m；結構第一振型阻尼比ξ1=0.05。隔震層質量 m =400×103 kg，隔震層等效圓頻率ω b =5.27 rad s，等效阻尼比ξb 分別取0.10，0.15，0.20，0.25，隔震層剛度 k = mωb（2）。隔震層設置帶支撐一般線性黏彈性阻尼器 PG （ t ），平衡剛度 k0=2.1×107 N /m，水平支撐剛度 kb =3k，松弛函數hQ （ t ）的拉氏和傅氏變換取二次分式：

其計算值取為：ωp =9.45 rad/s；d1=28.4 rad/s； e1=65 rad/s；e2=950 rad/s。

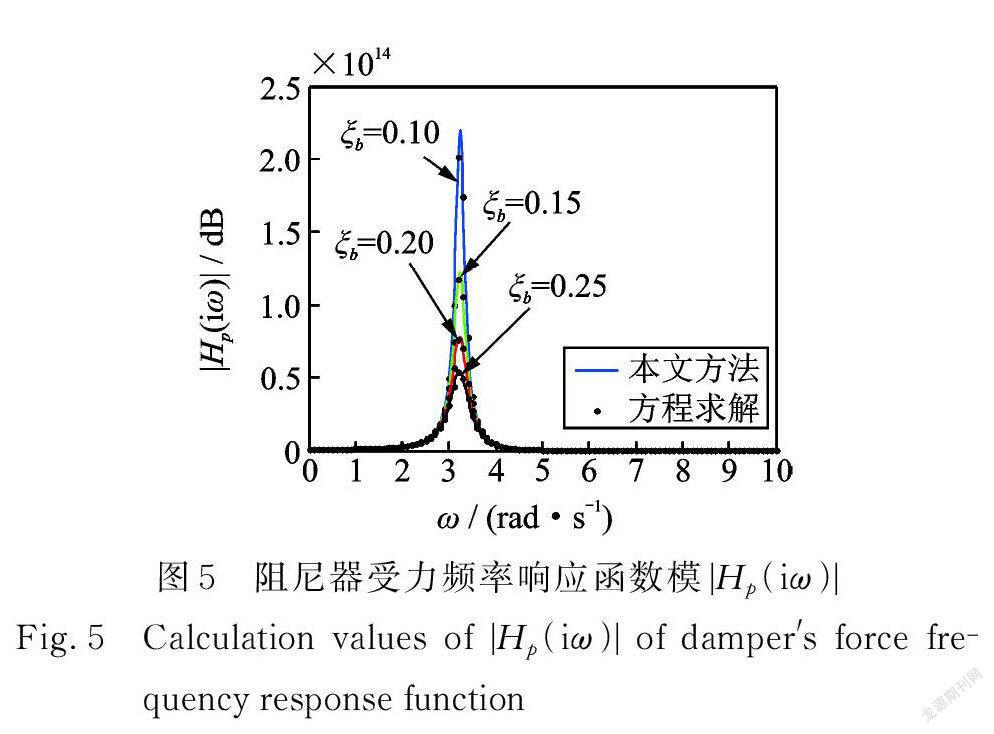
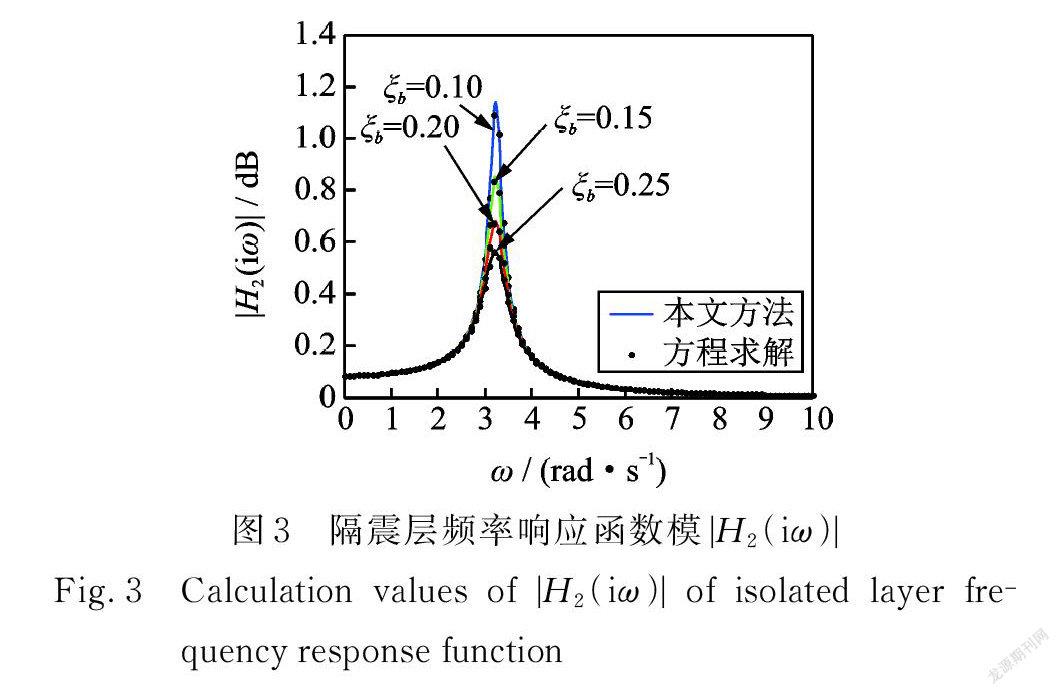
圖3～5分別為四種工況下，按照直接計算法和本文方法計算的結構隔震層頻率響應函數模、上部結構頻率響應函數模、阻尼器受力頻率響應函數模。由圖可知兩種求解方法所得結果完全一致，從而再次驗證了本文方法的正確性。

6.2.3 響應分析算例

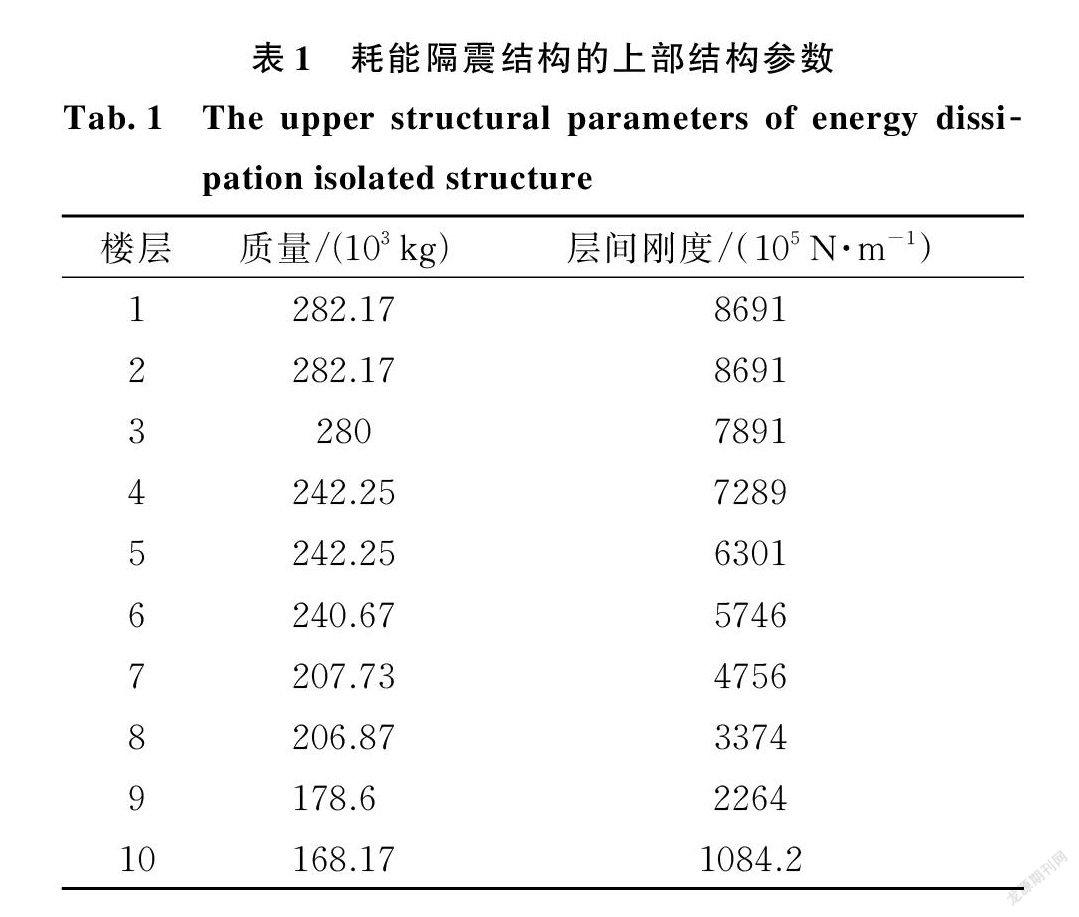
某10層框架隔震結構，結構第一振型阻尼比ξ1=0.05，結構參數如表1所示。隔震層質量 m =3.75×105 kg，等效阻尼比為ξb =0.2，隔震層剛度 k =9.04×107 N/m 。隔震層設置帶支撐的 Max ? well 阻尼器 PG （ t ），阻尼器參數為：平衡剛度 k0=0.36×105 N/m ，?? k1=42.08×105 N/m ；?? c1=0.83×105 N ? s/m，支撐剛度為 kb =3k。

平穩地震動 f （ t ）譜密度函數取為 Kanai ?Taji? mi 譜：

式中? S0為地震動譜強度；ωf 和ξf 分別為場地土的卓越頻率和阻尼比，ωf =19 rad/s，ξf =0.65。Shinzuka?Sato型均勻調制函數：

Spanos?Solomos型非均勻調制函數：

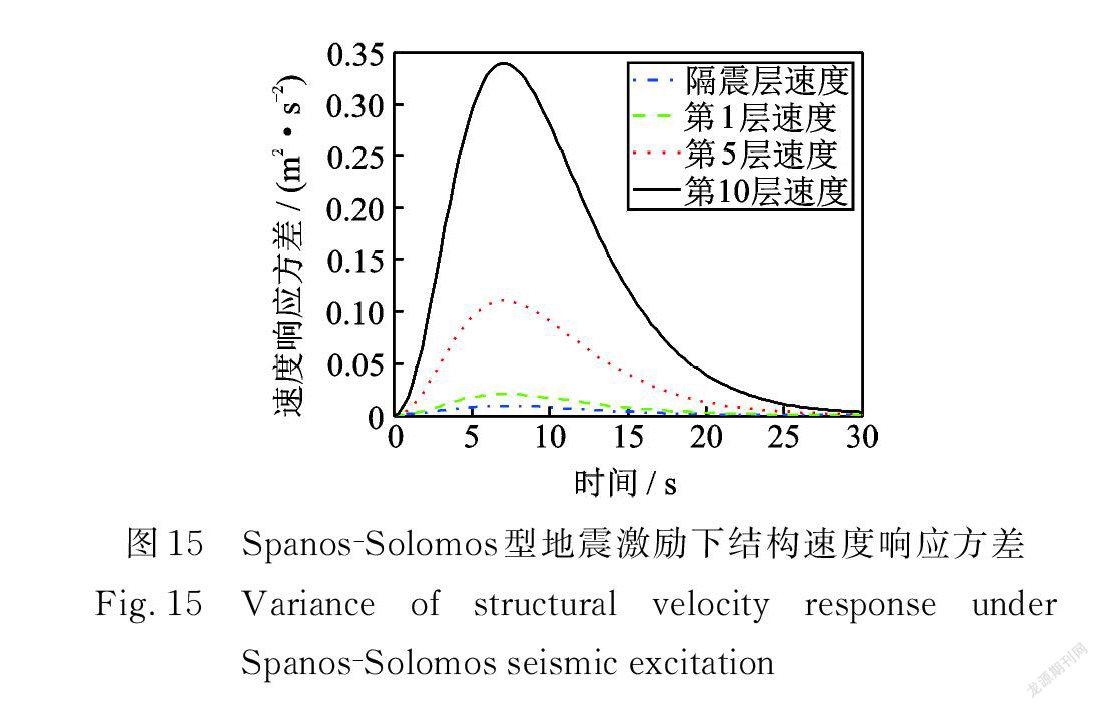
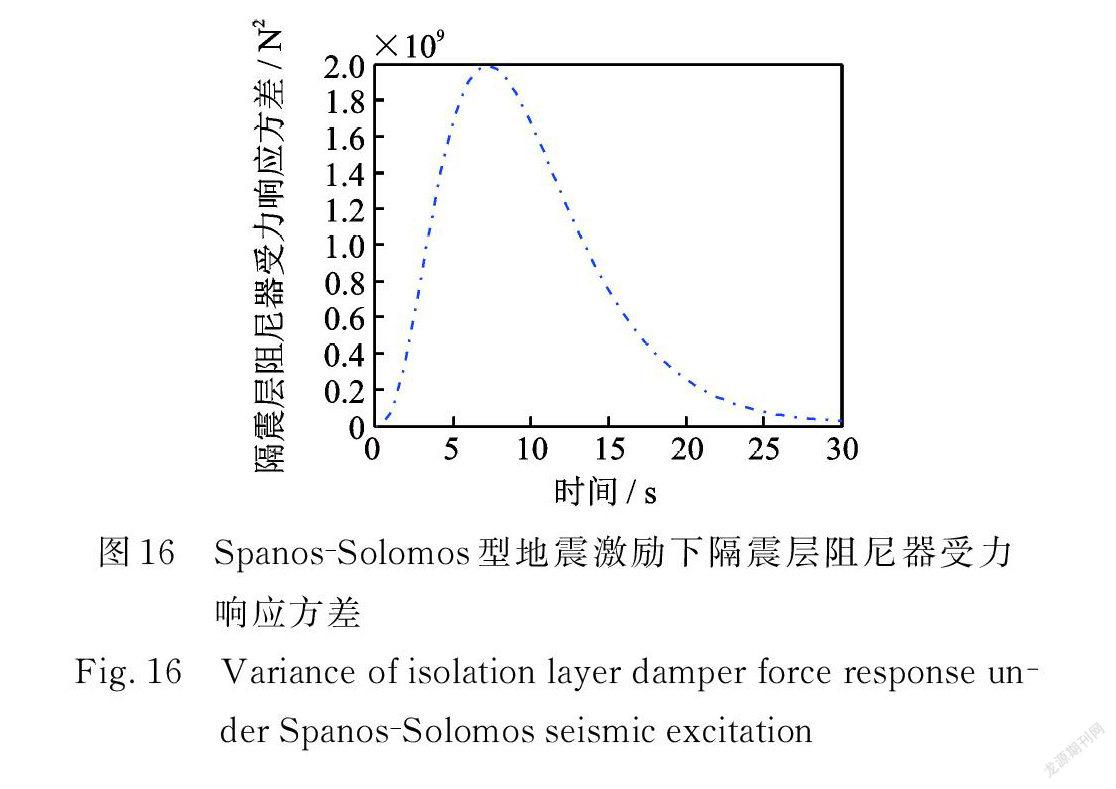
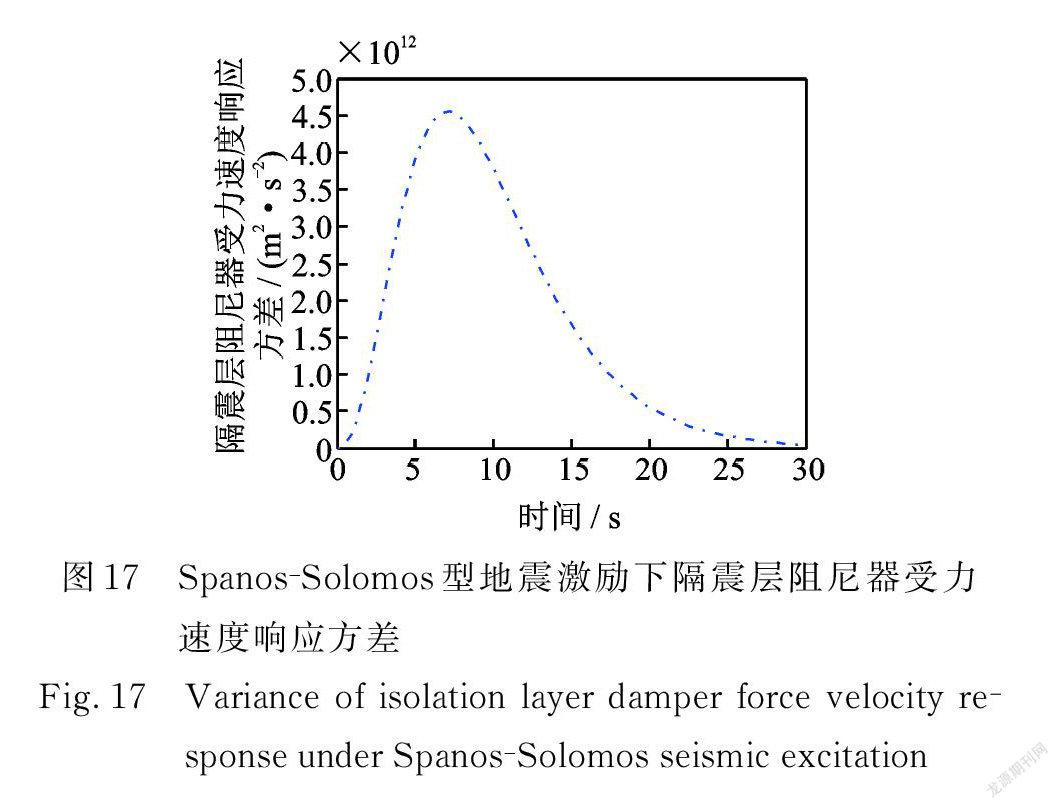
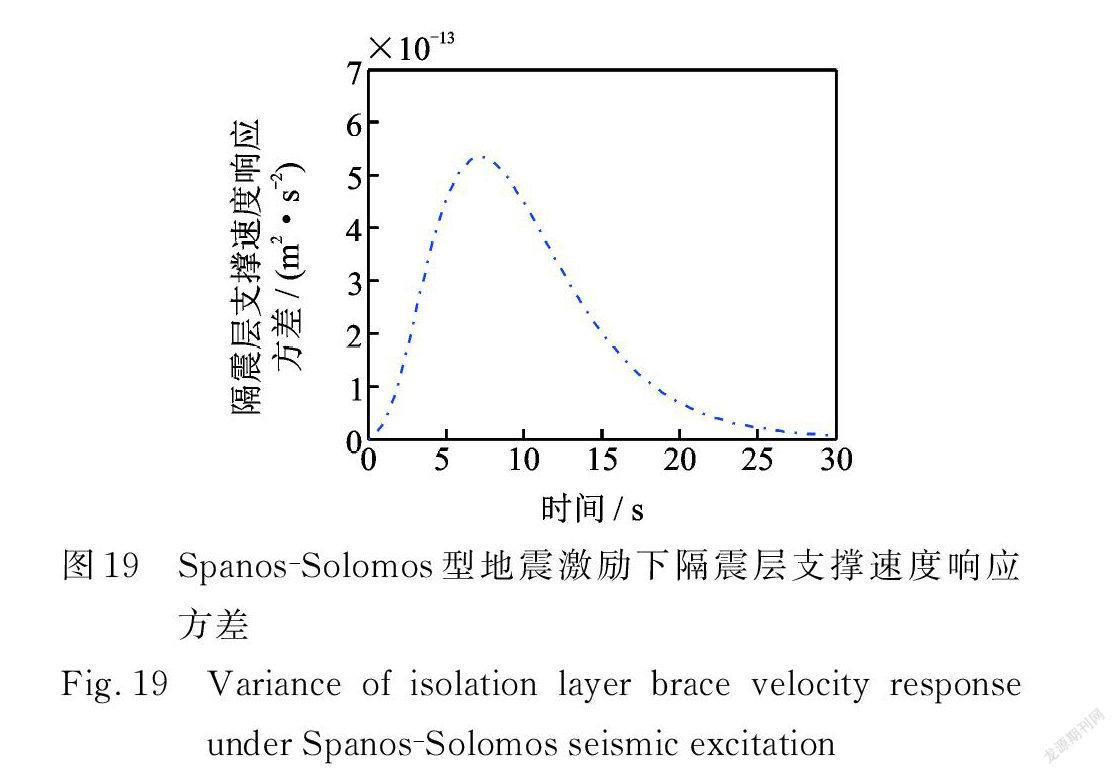
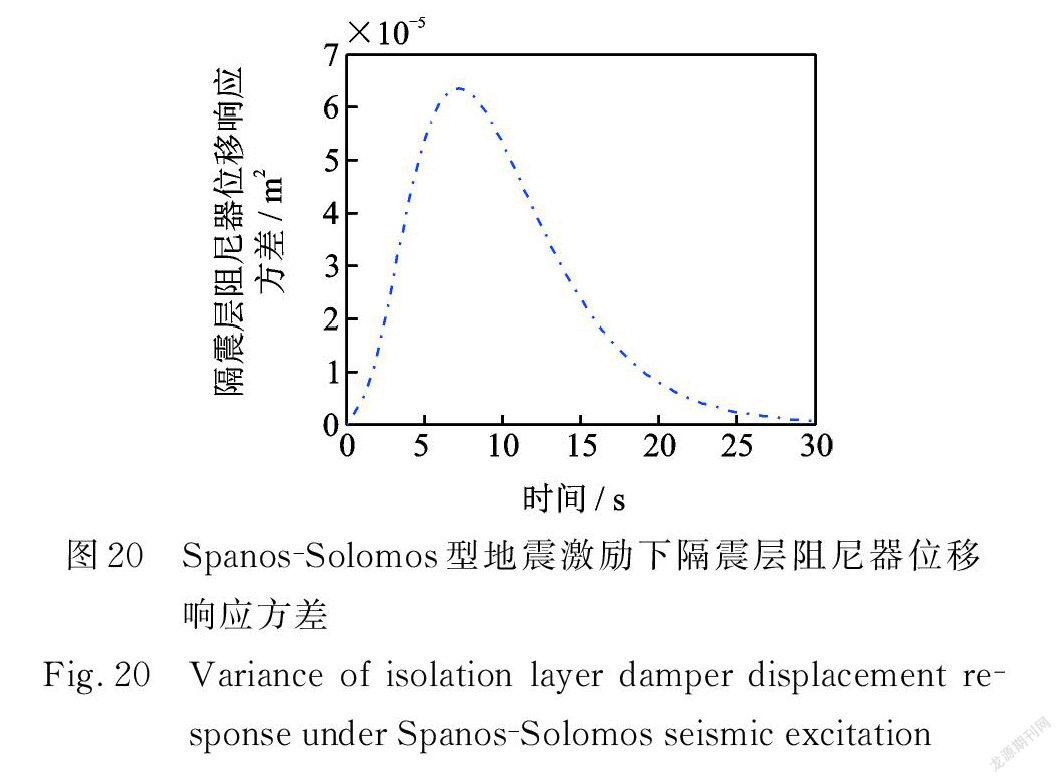
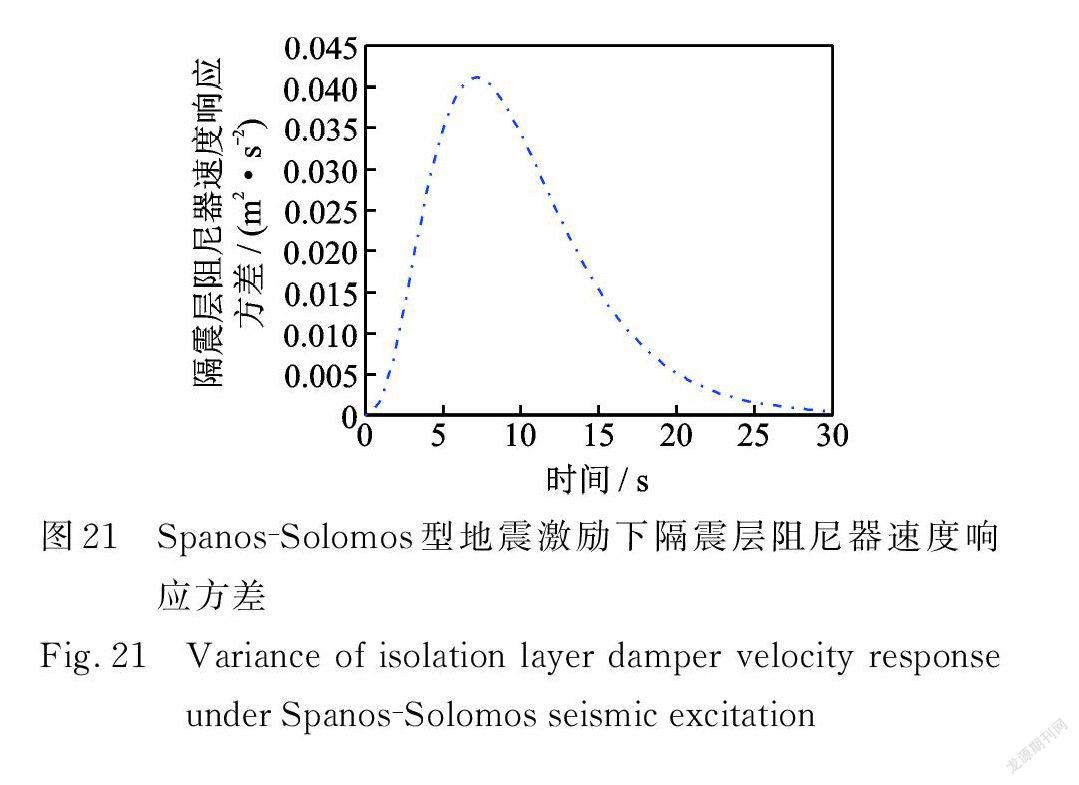
在 Spanos ? Solomos型非均勻調制非平穩地震激勵作用下，多層隔震結構系統的位移、速度，隔震層阻尼器受力、受力速率，隔震層支撐位移、速度，隔震層阻尼器位移、速度響應方差如圖14～21所示。

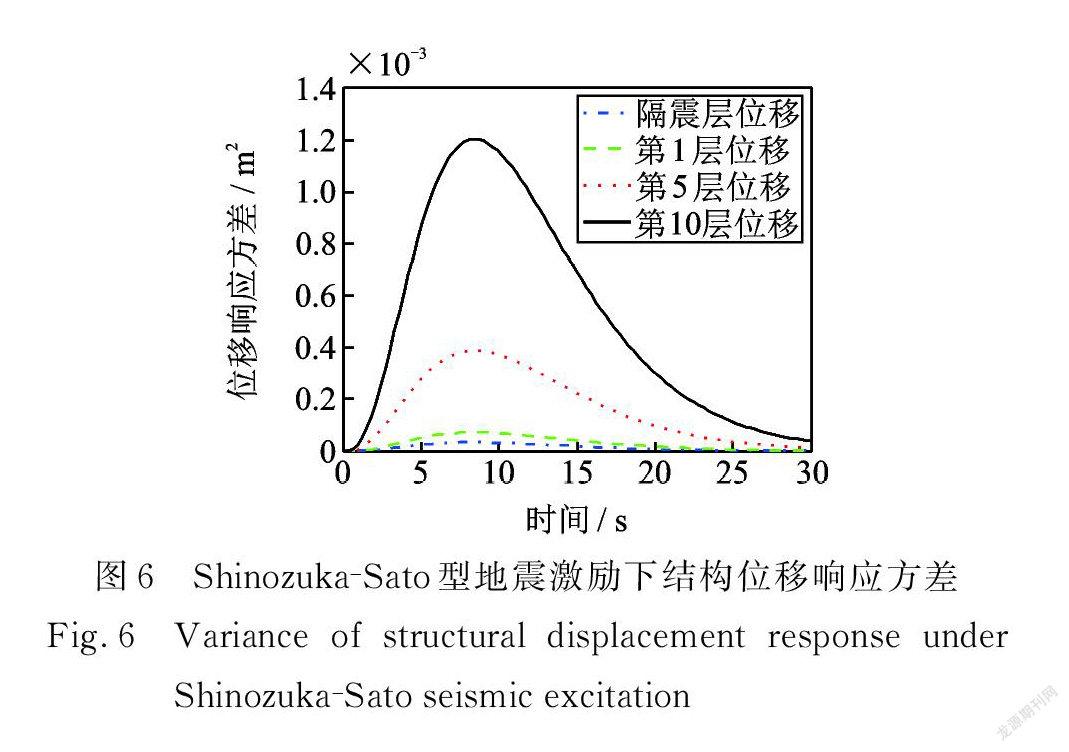
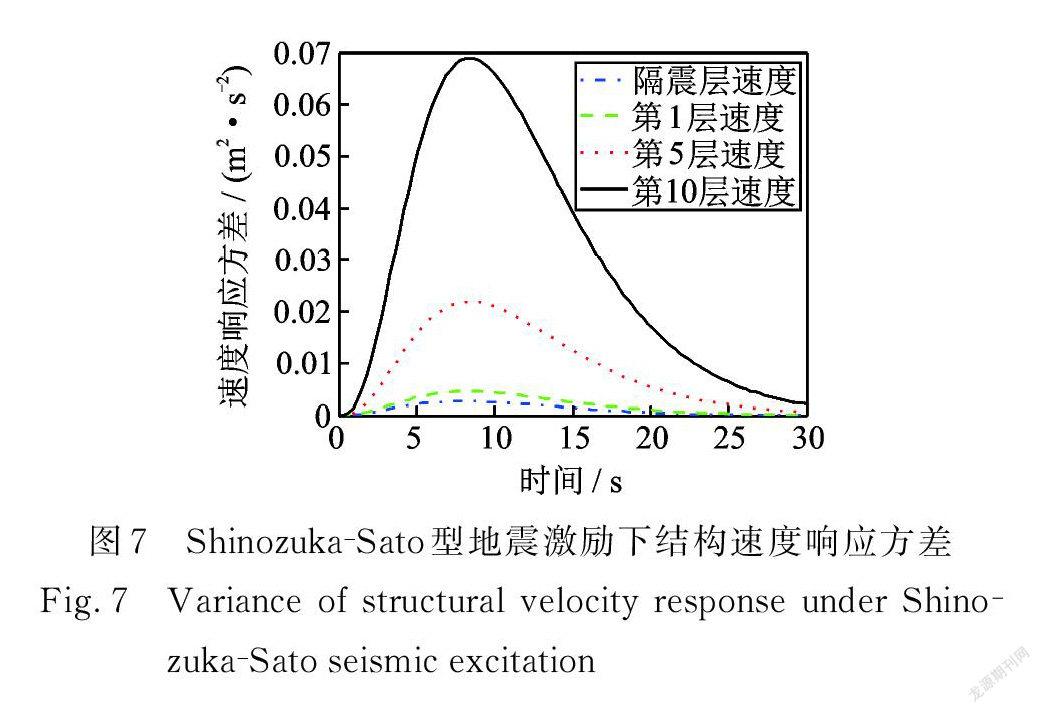
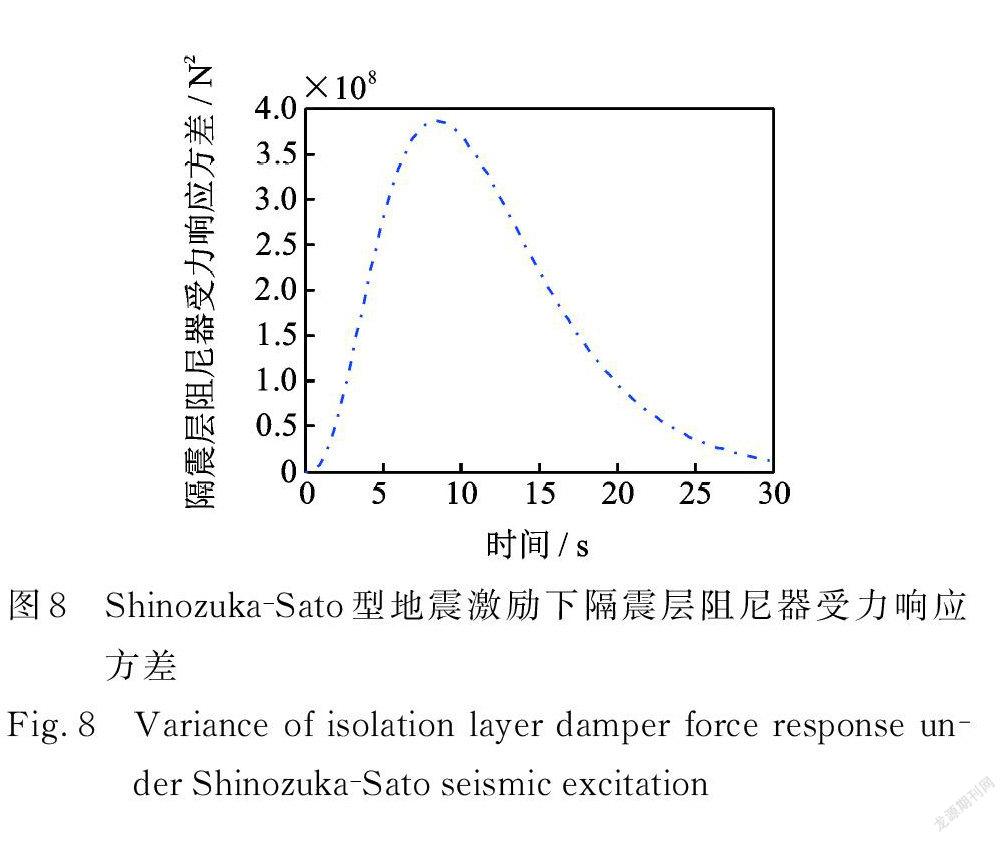
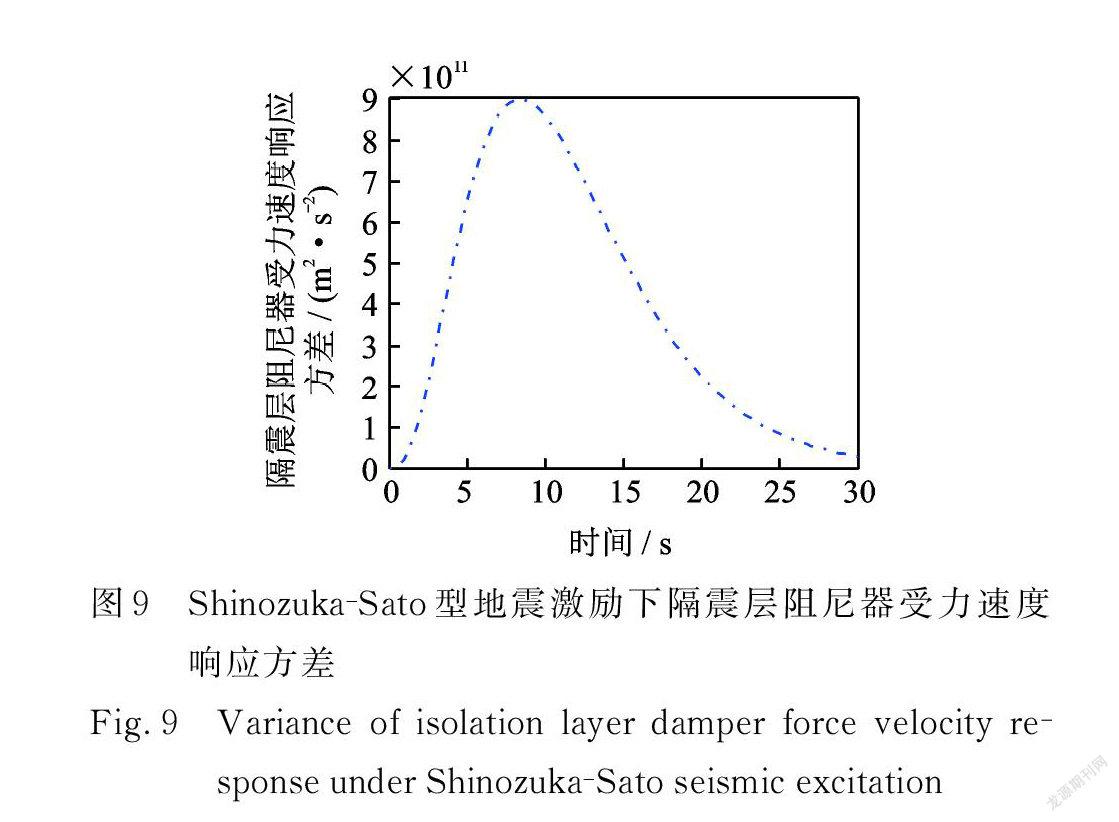
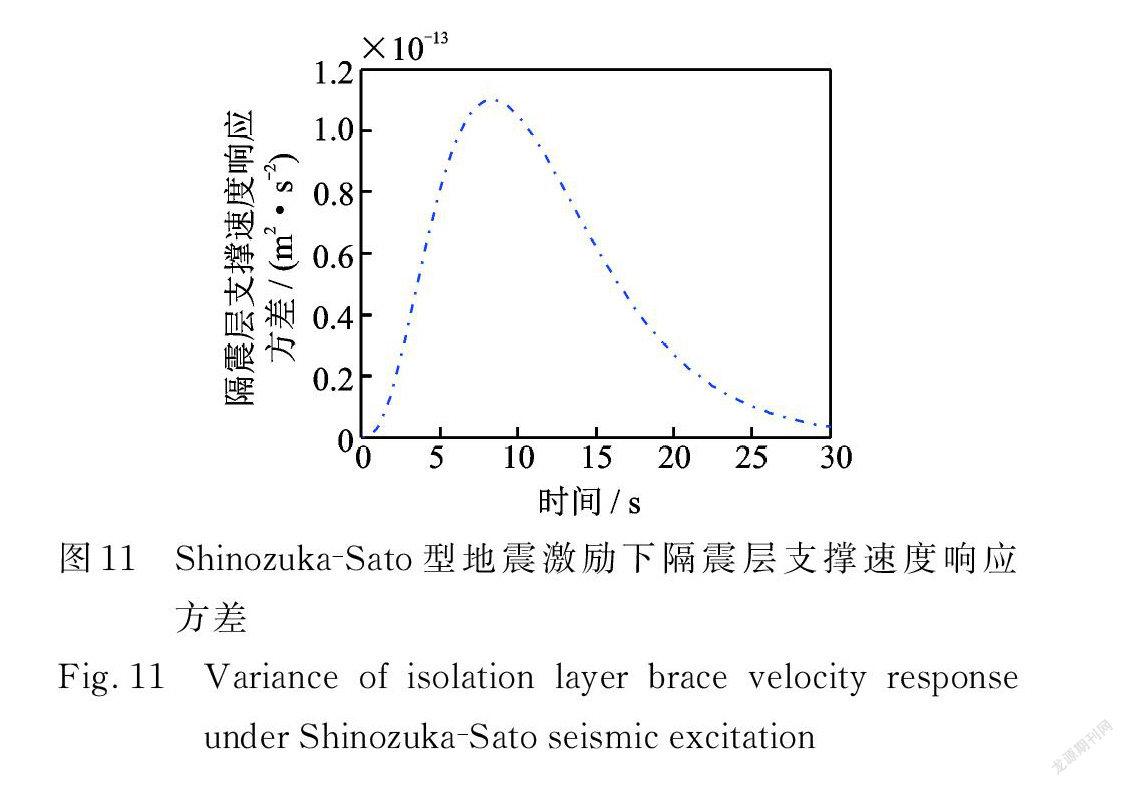
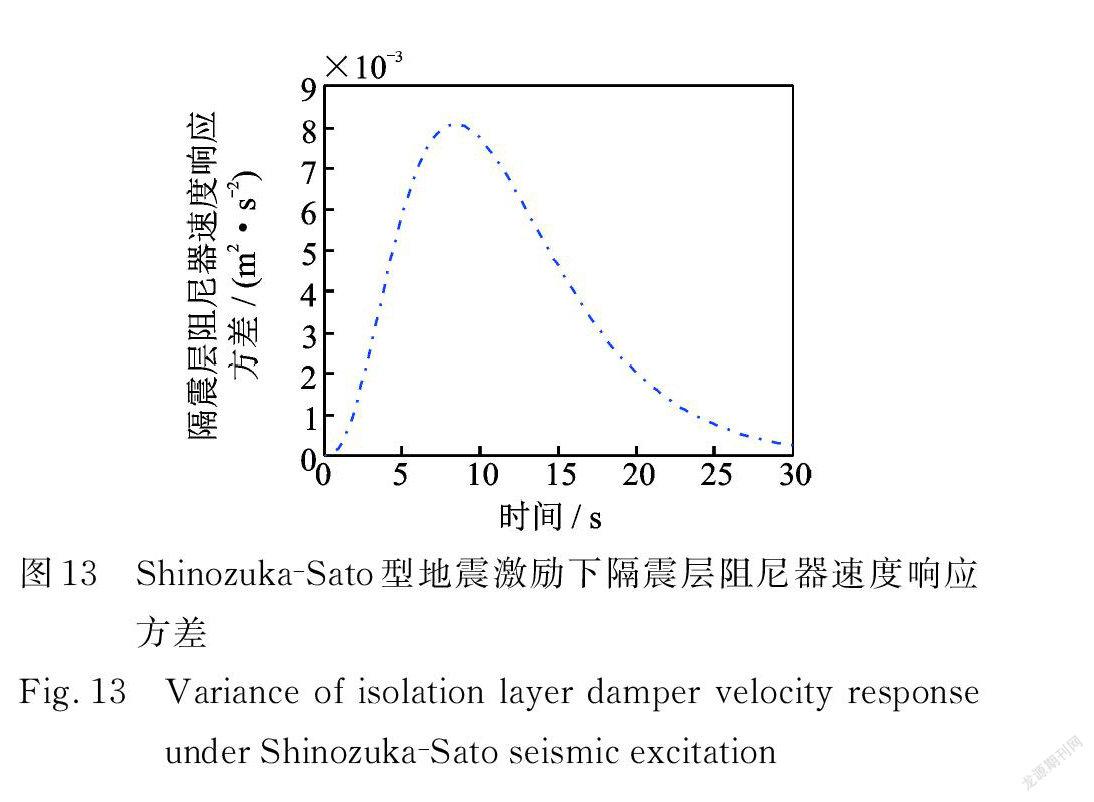
在Shinozuka? Sato 型均勻調制非平穩地震激勵作用下，結構響應方差具有峰值效應，且均在 t =8.4 s 同一時刻出現峰值，在 t=30 s之后響應方差收斂趨近于0。由圖6可得，結構第10層位移響應方差最大值僅為1.204×10-3 m 2，達到了很好的減震效果。 Spanos ? Solomos型與Shinzuka ? Sato 型非平穩地震激勵下，具有相似的性質：結構響應方差也具有峰值效應，且均在 t =7.2 s 同一時刻出現峰值，在 t =30 s之后響應方差收斂趨近于0。由圖14可得，結構第10層位移響應方差最大值僅為6.268×10-3 m 2，達到了很好的減震效果。

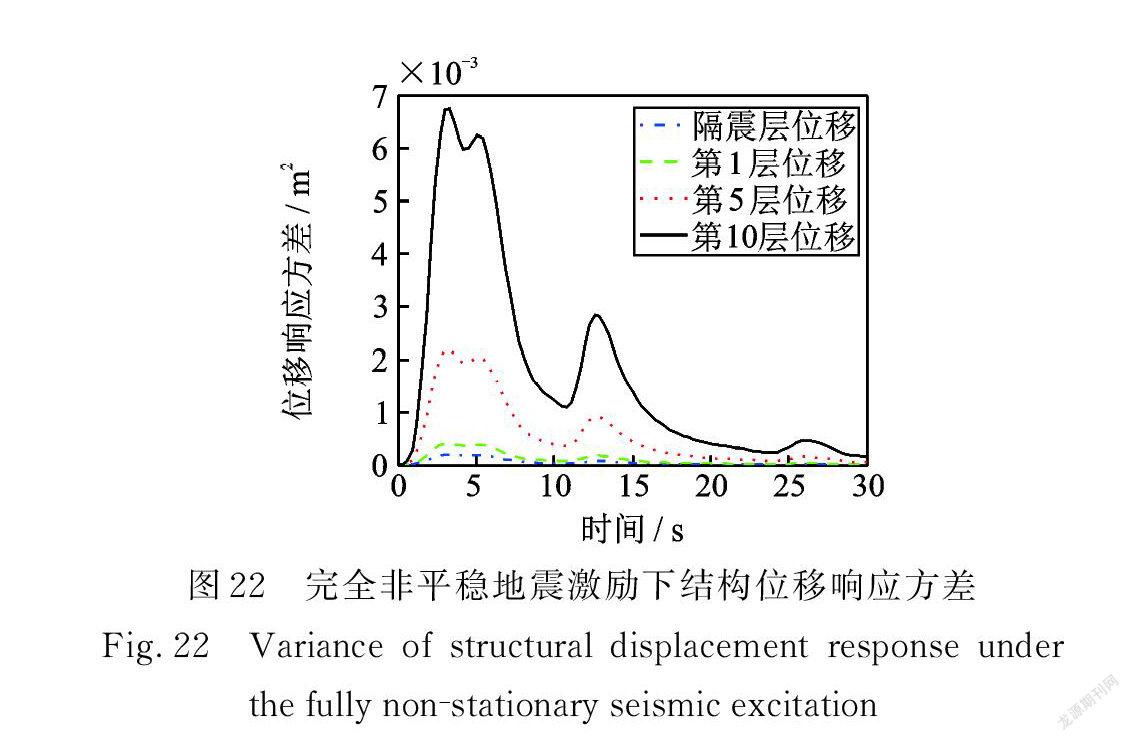
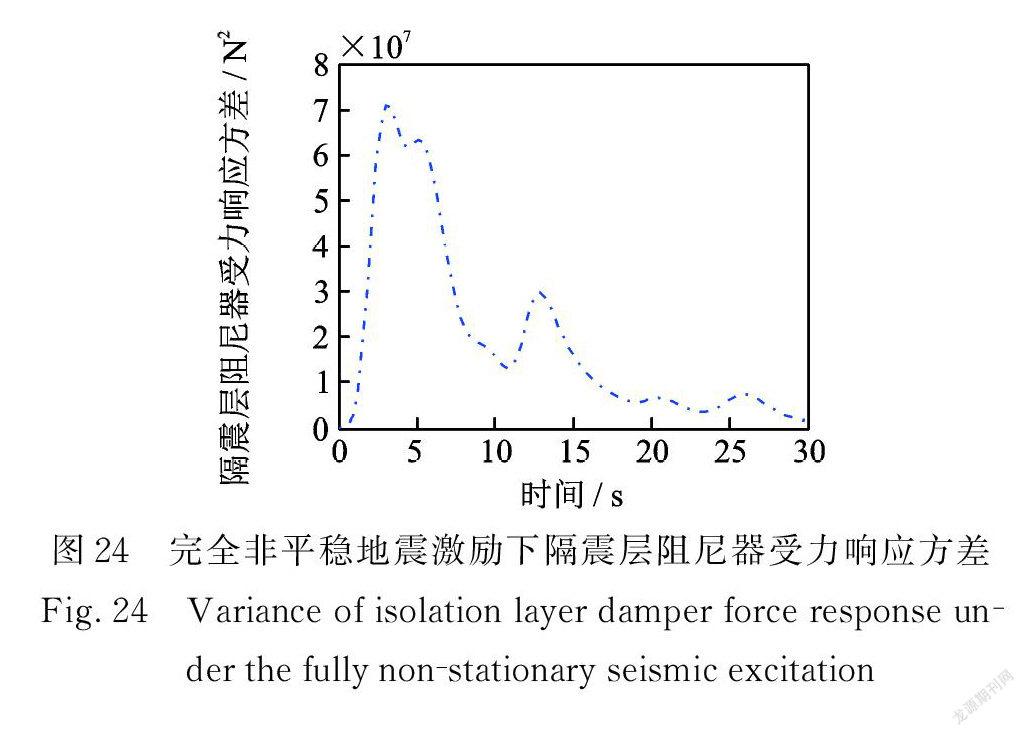
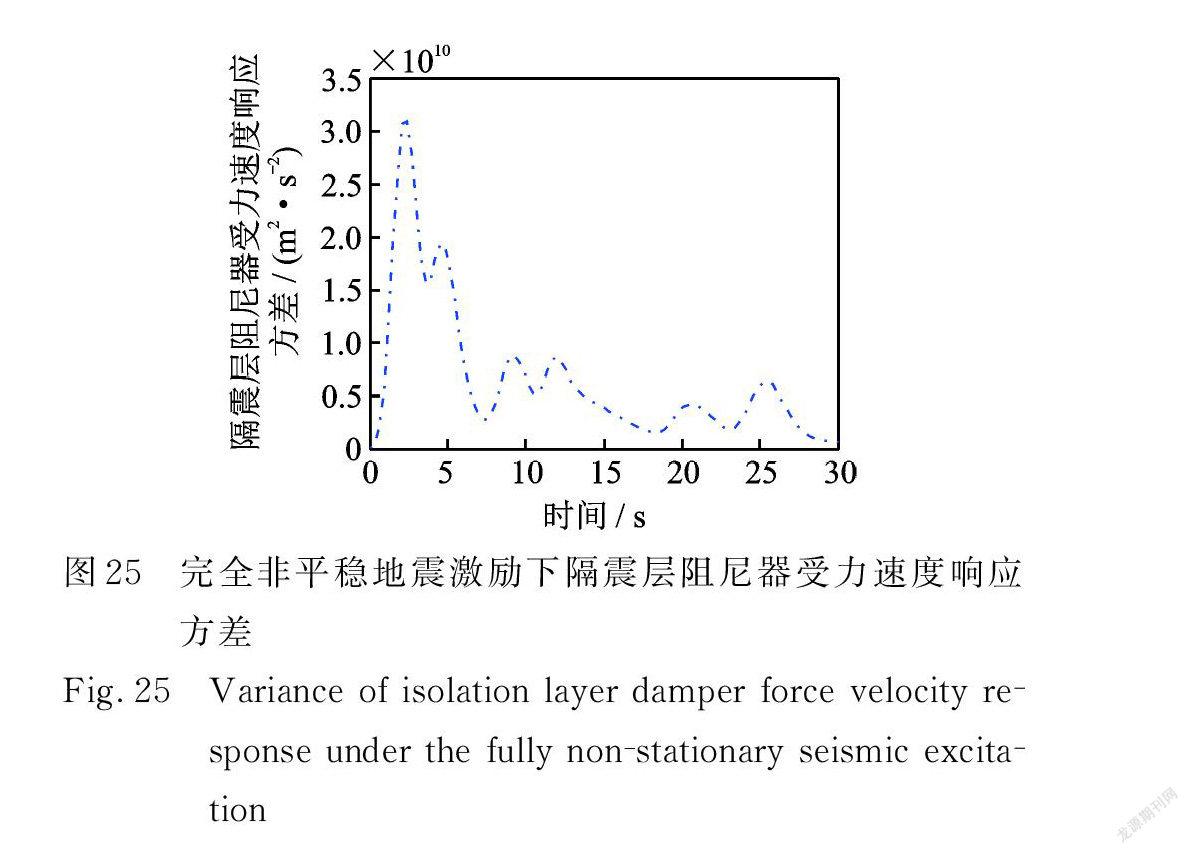
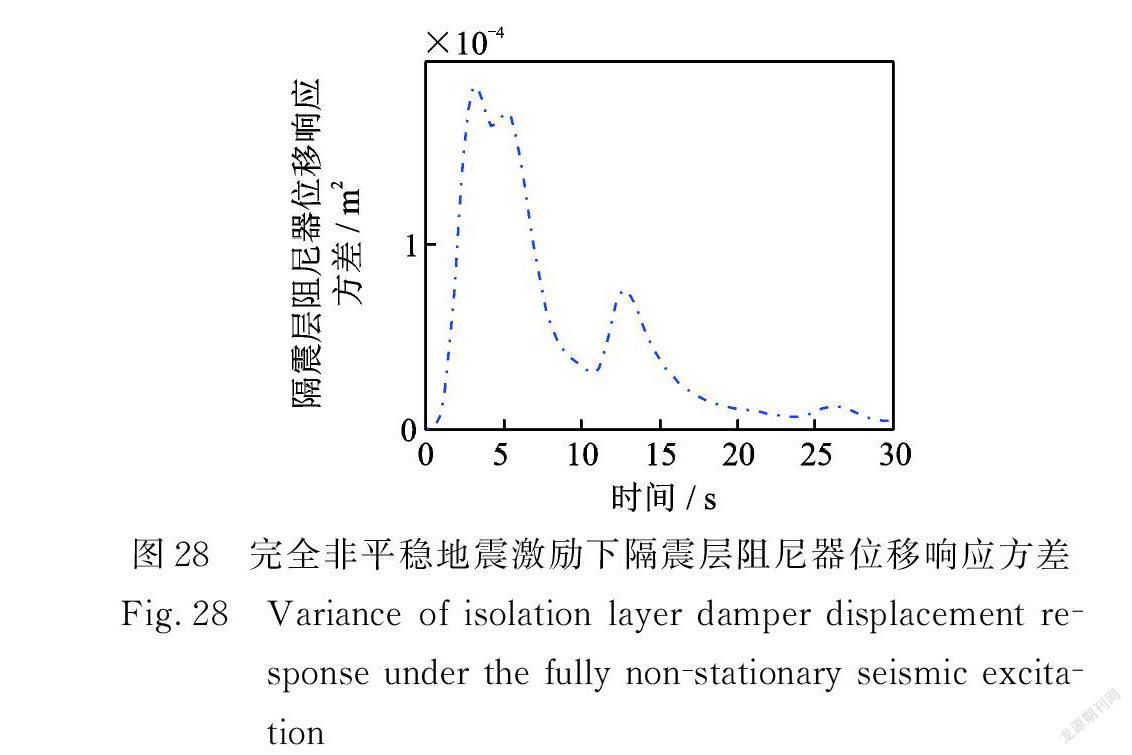
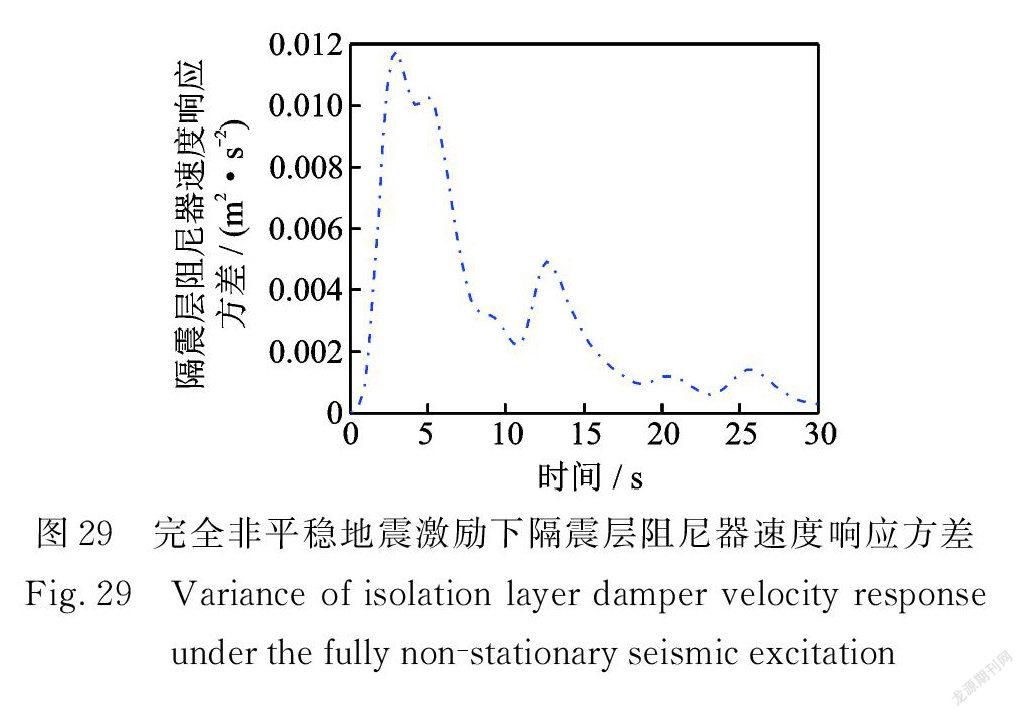
在完全非平穩地震激勵作用下，多層隔震結構系統的位移、速度，隔震層阻尼器受力、受力速率，隔震層支撐位移、速度，隔震層阻尼器位移、速度響應方差如圖22～29所示。

從以上結果可以看出：在Shinozuka ? Sato 型和Spanos? Solomos型調制非平穩地震激勵作用下，系統的非平穩響應方差與調制函數曲線相似，呈單峰形狀，即激勵模型方差是單峰的。由于完全非平穩地震激勵模型由多個均勻隨機過程疊加而成，完全非平穩地震激勵模型方差就是多峰的，并且完全非平穩地震激勵模型既與時間相關又與頻率相關，所以完全非平穩激勵下，系統的響應方差會呈現多峰狀，實際地震就是多峰的，更加符合工程實際意義。

在完全非平穩地震激勵作用下，響應方差呈多峰狀，取三次相對較大峰值進行分析，響應方差第一次出現峰值時間在 t=3.0～3.3 s，第二次出現峰值時間在 t =5.1～5.4 s，第三次峰值出現時間在 t =12.6～12.9 s，正是由于完全非平穩的特性導致出現峰值時間不是同一時刻，與 Spanos ? Solomos型和Shinzuka ? Sato 型不同。由圖22可得，結構第10層位移響應方差最大值僅為6.738×10-3 m 2，達到了很好的減震效果。

在三種非平穩地震激勵條件下均有：隨著層數的增加，結構的位移和速度響應方差也越大；第10層與第5層、第5層與第1層、第1層與隔震層響應方差的差值依次遞減；從隔震層阻尼器受力響應方差來看，阻尼器起到了很好的耗能作用。

7 結論

為建立設置支撐的一般黏彈性耗能結構阻尼器保護系統的抗震分析與設計方法，對設置支撐的一般黏彈性阻尼器耗能結構系統的瞬態響應模態疊加解析解進行了研究，并對其非平穩地震響應解析分析；獲得了設置支撐的一般黏彈性耗能結構阻尼器保護系統（結構位移與速度、阻尼器受力與受力速度、以及支撐和阻尼器的位移與速度）瞬態響應的非正交模態疊加解析解，應用此解析解和隨機振動頻域分析法，建立了設置支撐的一般線性黏彈性耗能結構阻尼器保護系統在一般和多種（Shinozuka? Sato 型、Hsu ? Bernard 型、Goto ? Toki 型、Iyengar 型、分段連續型、余弦型、正弦型、Spanos?Solomos型）均勻與非均勻非平穩激勵以及完全非平穩地震功率譜模型下的響應解析分析。

采用兩種典型結構系統（減震結構系統和隔震結構系統）的復模態法和頻響函數法的理論驗證分析，以及均勻、非均勻、完全非平穩算例響應分析，證明了本文方法的正確性、簡易性和普適性。

本文對設置支撐的一般線性黏彈性耗能結構阻尼器保護系統進行了分析，并使得非平穩地震激勵下響應分析應用更加廣泛和高效。通過對一般線性黏彈性耗能結構及阻尼器保護系統的瞬態響應和非平穩地震響應的解析分析，一方面可對整體耗能系統各構件進行基于泊松假設的抗震動力可靠度分析，另一方面將為結構系統建立基于反應譜的模態疊加抗震設計提供分析路徑。

參考文獻：

[1] 建筑抗震設計規范：GB 50011—2010[S].北京：中國建筑工業出版社，2010.

Code? for seismic design of buildings：GB 50011—2010[S]. Beijing：China Construction Industry Press，2010.

[2]? Christopoulos C，Filiatrault A，Bertero V V . Principlesof Passive Supplemental Damping and Seismic Isolation [M]. IUSS Press，2006.

[3] 周云.粘彈性阻尼器減震結構設計[M].武漢：武漢理工大學出版社，2006：116-128.

Zhou Yun . Viscoelastic Damping Structure Design[M]. Wuhan： Wuhan? University? of? Technology? Press，2006：116-128.

[4] 祝英杰.結構抗震設計[M].北京：北京大學出版社，2014.

Zhu? Yingjie . Structural? Seismic? Design [M]. Beijing： Peking University Press，2014.

[5]? Koh? C? G，Kelly? J M . Application? of fractional deriva?tives? to? seismic? analysis? of? base-isolated? models[ J ]. Seismic Engineering and Structural Dynamics，1990，19（2）：229-241.

[6]? Hwang J S，Ku S W . Analytical modeling of high damp?ing rubber bearings[ J ]. Journal of Structural Engineer? ing，1997，123（8）：1029-1036.

[7]? Makris N，Constantinou M C，Dargush G F . Analyticalmodel of viscoelastic fluid dampers[ J ]. Journal of Struc ? tural Engineering，1993，119（11）：3310-3325.

[8] 歐進萍，吳斌，龍旭.結構被動耗能減振效果的參數影響[ J ].地震工程與工程振動，1998，18（1）：60-70.

Ou? Jinping ，Wu? Bin ，Long? Xu . Parameter? analysis? of passive energy dissipation systems[ J ]. Earthquake Engi? neering? and? Engineering? Vibration ， 1998， 18 （1）：60-70.

[9] 翁大根，呂西林.消能減震結構設計參數研究與試驗驗證[ J ].地震工程與工程振動，2004，24（2）：150-157.

Weng Dagen，LüXilin . Study on design parameters of energy? dissipation? structures? with? experiment? verifica? tion[ J ]. Earthquake Engineering and Engineering Vibra? tion，2004，24（2）：150-157.

[10]歐進萍，龍旭.速度相關型耗能減振體系參數影響的復模量分析[ J ].工程力學，2004，21（4）：6-12.

Ou Jinping，Long Xu . Parameter analysis of passive en? ergy dissipation systems with velocity-dependent damp? ers [ J ]. Engineering Mechanics，2004，21（4）：6-12.

[11]常業軍，蘇毅，程文瀼，等.工程結構粘彈性消能支撐型式及設計參數的研究[ J ].地震工程與工程振動，2007，27（1）：136-140.

Chang Yejun，Su Yi，Cheng Wenrang，et al . Study on brace types and design parameters of engineering struc? tures? using? viscoelastic? dampers [ J ]. Earthquake? Engi?neering? and? Engineering? Vibration ， 2007， 27（1）：136-140.

[12] Fu Y，Kasai K . Comparative study of frames using vis?coelastic and viscous dampers[ J ]. Journal of Structural Engineering，1998，124（5）：513-522.

[13] Xie L，Cao M，Funaki N，et al . Performance study ofan? eight-story? steel building? equipped with? oil dampers damaged during the 2011 great? east Japan? seismic part 1：structural? identification? and? damage? reasoning [ J ]. Journal? of? Asian? Architecture? and? Building? Engineer? ing，2015，14（1）：181-188.

[14]建筑消能減震技術規程：JGJ 297—2013[S].北京：中國建筑工業出版社，2013.

Technical? specification? for? building? energy? dissipation： JGJ 297—2013[S]. Beijing：China Construction Indus ? try Press，2013.

[15]瞿偉廉，吳斌，李愛群.國家自然科學基金委員會工程與材料科學部.學科發展戰略研究報告——建筑、環境與土木工程Ⅱ（土木工程卷）：工程結構的振動控制理論及其應用[M].北京：科學出版社，2006：456-475.

Qu? Weilian，Wu? Bin ，Li Aiqun . National Natural? Sci? ence? Foundation? of Engineering? and? Materials? Science Department . Discipinary? Development? Strategy? Re? search? Report—— Structure ，Environmental? and? Civil Engineering （Civil? Engineering? Volume）：? Vibration Control Engineering? Structure Theory? and Its Applica? tions[M]. Beijing：Science Press，2006：456-475.

[16] Fang T，Li J Q，Sun M N . A universal solution for evo ?lutionary? random? response? problems [ J ]. Journal? of Sound & Vibration，2002，253（4）：909-916.

[17] Fang? T ，Zhang? T? S . Non-stationary? mean? square? re?sponse? due? to? uniformly? amplitude? modulated? random excitations[ J ]. Journal of Sound? and Vibration ，1955，182（3）：369-379.

[18]李創第，柏大煉，葛新廣，等.隔震結構系統線性黏彈性液體阻尼器非平穩響應分析法[ J ].振動與沖擊，2019，38（2）：234-246.

LI? Chuangdi ，BAI? Dalian ，GE? Xinguang ，et? al . Non stationary? response? analysis? of? isolated? structures? with linear viscoelastic? liquid dampers[ J ]. Journal of Vibra ?tion and Shock，2019，38（2）：234-246.

[19] Ou J P，Long X，Li Q S . Seismic response analysis ofstructures with velocity-dependent dampers[ J ]. Journal of? Constructional? Steel? Research ， 2007， 63（5） ：628-638.

[20]李創第，李暾，尉宵騰，等. Maxwell 阻尼耗能結構非平穩地震響應解析分析[ J ].振動與沖擊，2016，35（19）：172-180.

Li? Chuangdi ，Li? Tun，Wei Xiaoteng ，et? al . Response analysis? of? energy? dissipation? structures? with? Maxwell dampers? under? non-stationary? seismic? excitation [ J ]. Journal? of? Vibration? and? Shock ， 2016， 35（19）：172-180.

[21]李創第，李暾，葛新廣，等.一般線性黏彈性阻尼器耗能結構瞬態響應的非正交振型疊加精確解[ J ].工程力學，2015，32（11）：140-149.

Li Chuangdi，Li Tun，Ge Xinguang，et al . Accurate so ? lution? of? non-orthogonal? mode? superposition? for? tran? sient response of general linear viscoelastic damper ener? gy? dissipation? structures [ J ]. Engineering? Mechanics，2015，32（11）：140-149.

[22] Gluck N，Reinhorn A M，Gluck J，et al . Design of sup?plemental dampers for control of structures[ J ]. Journal of Structural Engineering，1996，122（12）：1394-1399.

[23] Council B S S .Prestandard and commentary for the seis?micrehabilitation? of buildings[ J ]. Report FEMA-356， Washington，D .C .，2000.

[24] Liang? Z ，Lee? G? C ，Dargush? G? F ，et? al . StructuralDamping：Applications? in? Seismic? Response? Modifica? tion[M]. CRC Press，2011.

[25]方同.工程隨機振動[M].北京：國防工業出版社，1995.

Fang Tong，Engineering Random Vibration [M]. Bei? jing：National Defense Industry Press，1995.

[26] PRIESTLEY M B . Power spectral analysis of non-sta?tionary random processes[ J ]. Journal of Sound and Vi? bration，1967，6（1）：86-97.

[27] Housner G W . Characteristics of strong motion seismics[ J ]. BSSA，1947，37：19-31.

[28] TajimiH . A statistical method of determining the maxi?mum? response? of a? building? structure? during? a? seismic [C]. Proceedings of the 2nd World Conference on seis? mic Engineering，1960（2）：781?796.

[29] Clough? R? W . Penzien? J . Dynamics? of? Structures[M].2nd ed . New York：McGraw Hill，1993.

[30]李鴻晶，陳辰.一種平穩地震地面運動的改進金井清譜模型[ J ].工程力學，2014，31（2）：158-163.

Li? Hongjing ， Chen? Chen . A? modified? Kanai-Tajimi spectral model for the stationary seismic induced ground motion? process [ J ]. Engineering? Mechanics ，2014，31（2）：158-163.

[31] Rofooei F? R，Mobarake A，Ahmadi G . Generation? ofartificial seismic records with a non-stationary Kanai? Ta ? jimi model[ J ]. Engineering? Structures，2001，23（7）：827-837.

[32]李創第，黃天立，李暾，等. TMD 控制優化設計及振動臺試驗研究[ J ].土木工程學報，2006，39（7）：19-25.

Li? Chuangdi ，Huang? Tianli ，Li? Tun ，et? al . Optimal TMD design and shaking table test[ J ]. China Civil En ? gineering Journal，2006，39（7）：19-25.

[33] Conte? J? P ，Peng? B? F . Fully? non-stationary? analyticalseismic? ground-motion? model[ J ]. Journal? of Engineer? ing Mechanics，1997，123（1）：15-24.

[34] Palmeri A，Ricciardelli F，Luca A D，et al . State spaceformulation for linear viscoelastic dynamic systems with memory[ J ]. Journal of Engineering Mechanics ，2003，129（7）：715-724.

[35] Singh M P，Verma N P，Moreschi L M . Seismic analy?sis and design with Maxwell dampers[ J ]. Journal of En ? gineering Mechanics，2003，129（3）：273-282.

[36]張天舒，方同.彈性-粘彈性復合結構系統的隨機響應分析[ J ].工程力學，2001，18（5）：71-76.

Zhang Tianshu，Fang Tong . The random response anal? ysis? of elastic-viscoelastic? combined? systems[ J ]. Engi? neering Mechanics，2001，18（5）：71-76.

[37]李創第，鄒萬杰，黃天立，等.結構在水平與豎向地震同時作用的非平穩響應[ J ].土木工程學報，2005，38（6）：25-34.

Li? Chuangdi，Zou? Wanjie，Huang? Tianli，et? al . Non- stationary? random? response? of structures? to? horizontal- vertical seismic excitations[ J ]. China Civil Engineering Journal，2005，38（6）：25-34.

[38]李創第，柏大煉，鄒萬杰，等.設置支撐的廣義 Maxwell阻尼器系統基于非平穩巴斯金譜的地震響應分析[ J ].應用力學學報，2018，35（5）：1050-1057.

Li Chuangdi，Bai Dalian，Zou Wanjie，et al . Analytical method? for non-stationary? responses? of dissipative? sys? tem? with? brace-general? Maxwell? damper? based? on Baskin? spectrum [ J ]. Chinese? Journal? of? Applied? Me? chanics，2018，35（5）：1050-1057.

Analytical analysis of non -uniform and completely nonstationary seismic response of a general linear viscoelastic damper protection system

LI Chuang-di1，WANG Bo-wen2，CHANG Ming-jing3

（1.School of Civil Engineering and Architecture，Guangxi University of Science and Technology，Liuzhou 545006，China；

2. School of Mechanics and Civil Engineering，China University of Mining and Technology，Xuzhou 221116，China；

3.School of Civil Engineering and Architecture，Wuhan University of Technology，Wuhan 430070，China）

Abstract： In order to establish the seismic design and a dynamic reliability analysis method of the damper protection system of gen ? eral linear viscoelastic energy dissipation structure with braces，a general analytical solution of the response of the damper protec? tion system of the general linear viscoelastic energy dissipation structure with braces under the non-uniform and completely nonsta? tionary seismic excitation is proposed in this paper . The most general integral type analysis model with support viscoelastic damper is used to realize the non-extended order modeling of the general linear viscoelastic damping energy dissipation structure system with braces by using differential integral equations . The non-extended order mode superposition solution of the transient response of the damper protection system under arbitrary excitation and non-zero initial conditions is directly obtained by using the transfer ma? trixmethod . By using the analytical solution and the frequency domain analysis method of random vibration，the specific response analytical solutions of the damper protection system of energy dissipation structure are obtained under the general and eight classical uniform and non-uniform modulation filtered white noise seismic excitation and completely non-stationary seismic power spectrum models . The correctness，simplicity and universality of this method are proved by the theoretical verification analysis of the com ? plex mode method and frequency response function method of two typical structures of vibration absorption and isolation，as well as the response analysis of uniform，non-uniform and completely non-stationary cases . The obtained analytical solutions of transient response and non-stationary seismic response can，on the one hand，carry out Poisson based analysis on the components of the overall energy dissipation system . On the other hand，it will provide an analysis path for the structural system to establish the mode superposition seismic design based on response spectrum .

Key words ： energy dissipation structure system；viscoelastic damper；transient response；non-uniform and completely non-station? ary response；analytical solution

作者簡介：李創第（1964—），男，博士，教授。E-mail：lichuangdi1964@163.com。