非線性多自由度系統的數據驅動建模和響應預測

蔡君同 尹強 丁千

摘要：由于工程系統的復雜性和參數不確定性，利用力學原理建立的動力學控制方程常難以滿足精度需求。基于數據驅動的系統建模和響應預測，利用動力學狀態方程的數值解模擬實驗中測得的不同外激勵下的系統響應，并用于訓練神經網絡，構建包含訓練數據間已知關系的損失函數以提高模型精度，得到表達系統狀態關系的數據模型。將該神經網絡模型納入常微分方程求解器，可預測系統在不同激勵下的響應，并獲得幅頻響應關系。將建模方法分別應用于含立方型和間隙型非線性的彈簧質量系統，計算結果表明，可根據響應數據建立準確的數據模型，并獲得非線性系統主共振時的滯后和跳躍響應。研究還表明，訓練數據越多、數據覆蓋狀態越完整，數據模型精度越好，且預測響應的誤差越小。

關鍵詞：非線性系統；數據驅動；系統建模；響應預測

中圖分類號： O322；O313.3??? 文獻標志碼： A??? 文章編號：1004-4523（2022）05-1101-08

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.007

引言

隨著工程中研究對象的復雜化，建立準確的系統動力學控制方程越來越困難。利用力學原理，在各種假設條件基礎上建立的模型，常常難以反映真實動力學特性，響應預測精度也往往難以滿足要求[1]。大數據科學的快速發展為基于系統響應數據的動力學系統建模和響應預測帶來了可能性[2]。

基于數據的系統分析方法分為參數方法和非參數方法。參數方法通常需要一個假設模型，并進行初始參數化。利用系統響應數據，通過最小二乘和最大似然估計法來減小模型預測誤差，實現模型參數的更新[3?5]。在處理非線性動力學問題時，通常假設初始模型結構為雙線性結構、Duffing 結構或滯回結構[6?7]。非參數方法包括小波變換、Hilbert?Huang變換、神經網絡方法等，不需要關于系統的先驗信息。其中，神經網絡[8]具有很強的非線性擬合能力，通過數據訓練可映射任意復雜的非線性關系，可直接建立輸入與輸出數據之間的映射關系，是最受關注的復雜系統動力學建模方法。Pei 等[9?10]利用神經網絡擬合非線性回復力。Derkevorkian等[11]將神經網絡與常微分方程（ODE）求解器相結合，模擬土體結構相互作用并預測系統響應。Witters等[12]建立神經網絡的客車半主動阻尼器模型，該模型能夠準確、有效地描述阻尼器的動態特性。基于機器學習算法的數據驅動建模，大都把狀態向量的時間導數數據看作已知。因為導數運算對采集數據中噪聲因素非常敏感，若不能準確獲得狀態向量的導數數據，就會產生較大誤差。Raissi等[13]采用線性多步法限制狀態向量與其導數之間的關系，減少了獲取數據過程產生的誤差。

利用神經網絡求解常/偏微分運動方程也是近年來研究熱點之一。將神經網絡的輸出作為方程的一個候選解，通過訓練來更新網絡權重參數從而降低控制方程的不平衡，繼而使候選解不斷接近真解。例如，Chen 等[14]利用深度神經網絡求解常微分方程，采用常規算法驗證結果的準確性。Raissi等[15] 利用神經網絡對時間離散和時間連續的兩類偏微分方程模型進行求解及辨識。Wei 等[16]基于深度強化學習理論對范德波方程及經典偏微分方程求解，結果表明對穩定周期解求解精度高、速度快。但相較于偏微分方程，常微分方程計算問題中所得的神經網絡大多只對當前數據集有效，主要原因是損失函數對模型訓練過程的約束較弱，導致訓練后的神經網絡不能很好地逼近理論模型。因此，進行數據驅動的動力學研究，不能僅僅著眼于數據本身，更要關注其代表的物理含義，借用力學特征從數據間挖掘潛在的動力學規律。

研究動力學問題時，很多工程系統都可以簡化成單自由度或多自由度彈簧質量系統，同時也考慮阻尼、間隙等因素的影響。考慮到工程系統的復雜性和參數不確定性，基于力學原理常難以建立滿足需求的模型，因此本文研究數據驅動的非線性動力學系統建模，并基于數據模型的響應預測結果，驗證數據模型的有效性。本文研究非自治動力學系統，其狀態方程形式下外激勵項與響應項不存在耦合關系。首先給出建模流程，即由已知動力學狀態方程獲得若干外激勵下的響應數據，并作為神經網絡的訓練數據，用來使神經網絡代替狀態方程中含有響應項的部分。同時利用訓練數據間已知關系構建損失函數，從而提高數據模型精度。然后將該方法應用于單自由度和三自由度彈簧質量系統，通過 ODE 求解器獲得訓練后的系統幅頻響應曲線，討論訓練數據噪聲和訓練數據特征對數據模型精度的影響。

1? 問題描述

考慮一個非自治動力學系統：

式中? u （ t ）=[ u1（ t ） u2（ t ）… un （ t ）]T ∈ Rn 為位移向量；M 為質量矩陣；G（ u（ t ），u? （ t ））為廣義回復力；F （ t ）為外激勵力。

將方程（1）寫成以下狀態方程形式：

式中 v （ t ）=[ v1（ t ） v2（ t ）…vn （ t ）]T ∈ Rn 為速度向量。為簡便起見，進一步將方程（2）表示為：

式中? X （ t ）=[ uT （ t ） vT （ t ）]T ∈ R 2n 為系統的狀態向量，f （X （ t ））∈ R 2n，fˉ（t ）=[01× n （ M -1 F （ t ））T ]T ∈R 2n。

本文研究 G（ u，u? ） 為未知時的數據建模，因其包含在f（ X ）中，將利用已知的輸入輸出數據訓練一個神經網絡f?（ X ）來代替f（ X ），從而得到可用于動力學計算的數據模型。基本做法是：求解已知狀態方程（模擬實際測量），得到對應于外激勵fˉ（ t ）的狀態向量響應數據 X（ t ），用于訓練神經網絡f?（ X ），使其反映從 X 到f（ X ）的映射關系。將訓練后的神經網絡代入式（3），便可獲得用于響應預測的狀態方程：

給定方程外激勵fˉ（ t ）及狀態初始值 X（ t0），即可利用 ODE 求解器求解、分析動力學系統（4）的響應 X （ t ）。

2? 求解方法

2.1? 線性多步法

用線性多步法求解常微分方程初值問題，是利用已知的前 k 個時刻的狀態向量表示下一時刻的狀態向量，其優勢是既保證計算精度，又不會增加太多計算量[17]。

為求解ti +1時刻的狀態向量 X（ ti +1），k 步線性多步法計算格式為：

式中i = k -1，…，N -1，αp 與βq 為常數，h 為數據采樣時間間隔，N 為數據采樣點數。當β-1= 0時，上式是顯性線性多步格式；當β-1≠ 0時，上式是隱性線性多步格式。公式（5）給出了 k+1個時刻的狀態向量 X 及方向場 X? 之間滿足的定量關系。將方程（3）代入式（5），可得：

由于提供了狀態向量與狀態方程（3）右端項之間的約束關系，方程（6）將用于神經網絡中損失函數的構建。

2.2? 數據驅動的動力學系統建模流程

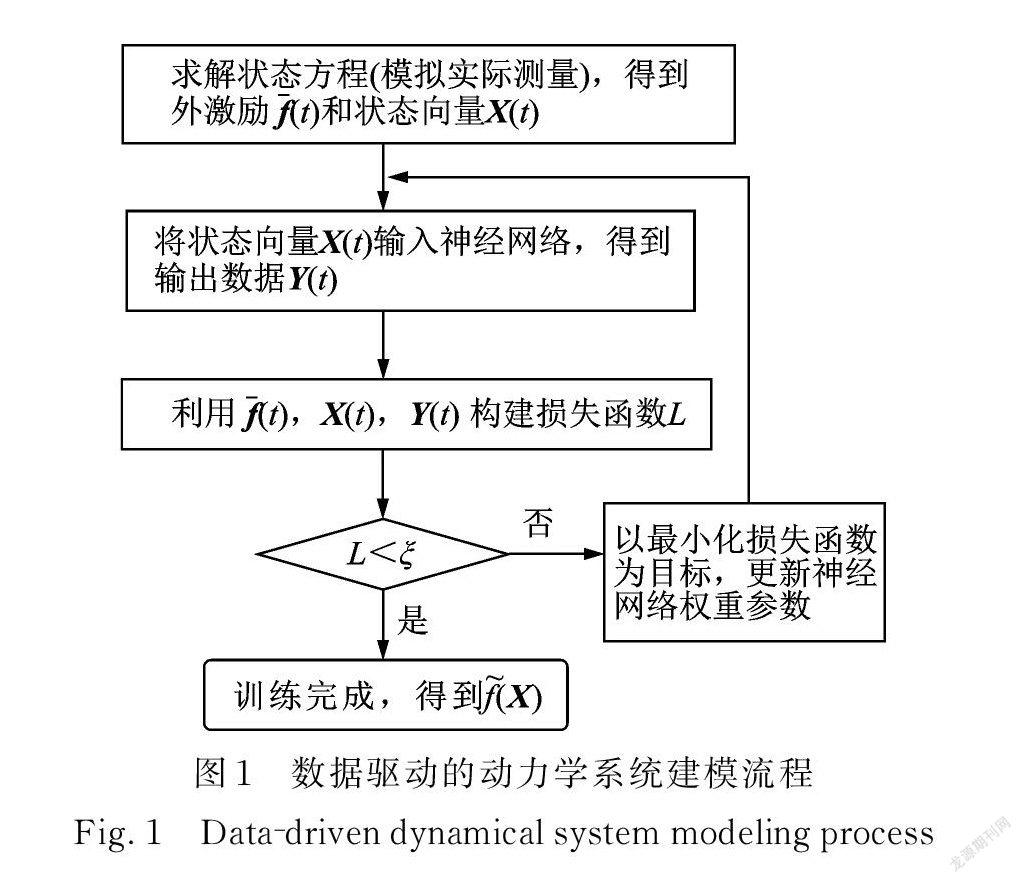
已知若干外激勵和相應的系統響應數據，進行系統數據驅動的動力學建模流程如圖1所示。

1）獲取神經網絡訓練數據。給定 M 個不同頻率和幅值外激勵的時間序列數據fl（-）（ tj ），l=1，…， M；j=0，1，…，N，利用 ODE 求解器對已知的狀態方程直接求解，獲得相應的系統狀態向量的時間序列Xfl（-）（tj ），用其模擬工程中實際測量數據。

2）訓練神經網絡f?（ X ）。將以上狀態向量數據 X （tj ）作為神經網絡的輸入數據，神經網絡的輸出數

據 Y （tj ）應滿足 Y （tj ）=f?（ X （tj ））。

根據線性多步法，公式（6）給出了神經網絡的輸入與輸出數據應該滿足的定量關系，即：

為提高神經網絡的模型精度，根據狀態向量中位移變量和速度變量的已知關系，構建網絡訓練的損失函數。損失函數是衡量神經網絡輸出數據與理論數據之間差距大小的指標，網絡訓練的本質正是最小化損失函數的過程。定義 X（tj ）中前 n 維數據為 X1（tj ），后 n 維數據為 X2（tj ）；同理，定義輸出數據 Y （tj ）中前 n 維數據為 Y1（tj ），后 n 維數據為 Y2（tj ）。

根據方程（2），（3）可得

根據線性多步法給定的神經網絡輸入輸出數據之間關系（7）及由訓練數據間的已知關系確定的部分神經網絡映射信息（8），給出了神經網絡訓練過程的損失函數 L 為：

式中γ為一常數，且：

利用神經網絡的輸入與輸出數據構建損失函數 L 后，以最小化損失函數為目標，用 Adam 方法[18]優化、更新神經網絡的權重參數。當損失函數數值下降到所需精度ξ時，認為神經網絡已完成訓練并停止迭代。

激活函數也是神經網絡的重要組成部分之一。考慮到訓練數據及其導數的連續性，激活函數選為 tanh 函數。神經網絡設定為一個隱藏層，每層256個神經元。綜上，通過訓練得到狀態方程（4）中的神經網絡f?（ X ）。

3）將神經網絡f?（ X ）代入狀態方程（4），并利用 ODE 求解器求解和預測外激勵fˉ（ t ）變化情況下系統狀態向量的響應 X（ t ）。

為直觀表現建立的數據模型在外激勵變化情況下的響應預測效果，改變方程（4）中外激勵fˉ（ t ），利用 ODE 求解器多次求解，得到系統在不同激勵力下的狀態響應 X（ t ），取穩定狀態下 X（ t ）中的位移幅值。通過正向和反向掃頻計算，得到幅頻響應曲線以檢驗數據驅動建模能否反映共振幅值跳躍的非線性現象。

3 數值算例

針對單自由度及三自由度非線性振動系統，研究上述數據驅動的系統建模和響應預測能力。為保證工程應用情況下的有效性，著重探究訓練數據中噪聲和訓練數據特征對數據模型精度的影響。

3.1? 立方非線性的單自由度彈簧質量系統

考慮帶有立方非線性的單自由度彈簧質量系統，如圖2所示。

動力學狀態方程為：

其中：

考慮系統維度較低，將線性多步法公式（7）簡化為以下隱性單步形式：

對應的損失函數為：

其中：

根據圖1的流程，利用已知的外激勵及響應數據訓練神經網絡，代替狀態方程中的f（ u1，v1）。

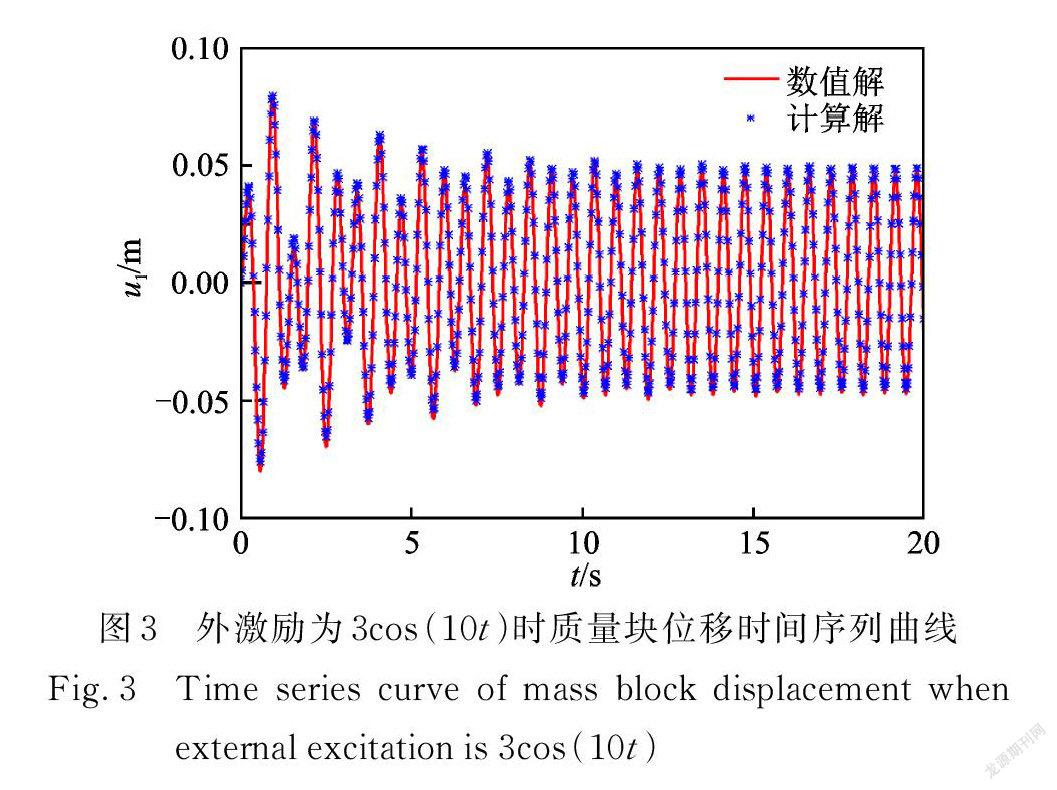
假設 m 1=1 kg，c1=0.5 N·s/m，k1=36 N/m， k2=150 N/m3，即無阻尼固有圓頻率為6 rad/s 。通過 ODE 求解器計算動力學狀態方程（11），并利用方程數值解來模擬系統在外激勵幅值 A=3 N 、外激勵頻率ω=6，7，8 rad/s 時的時域響應數據，采樣時長0～30 s，采樣頻率100 Hz 。將訓練后的神經網絡作為方程（4）的廣義回復力，利用 ODE 求解器計算外激勵為3cos（10t ）時的時域響應數據，預測的質量塊位移曲線如圖3所示。

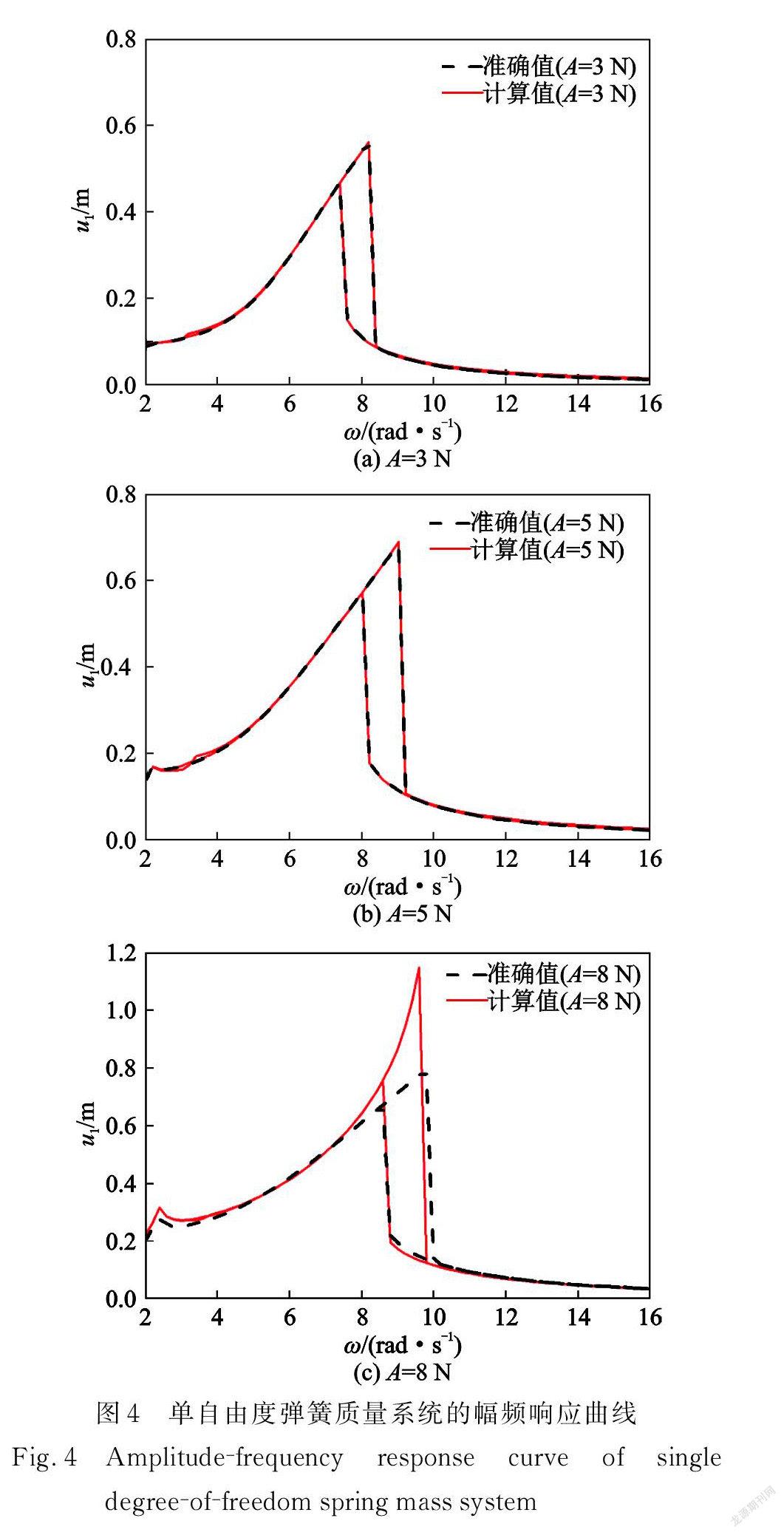
圖3中實線表示求解已知動力學狀態方程（11）的數值解，星號是基于數據模型的計算解，兩者差距極小。圖 4（ a ）為幅頻響應曲線的對比。激勵幅值提高到5 N，也能得到較好的預測結果，如圖4（b）所示。但當 A=8 N 時，由于預測工況與訓練工況的激勵幅值相差過大，數據模型的共振區響應預測精度相對變差，如圖4（ c ）所示。

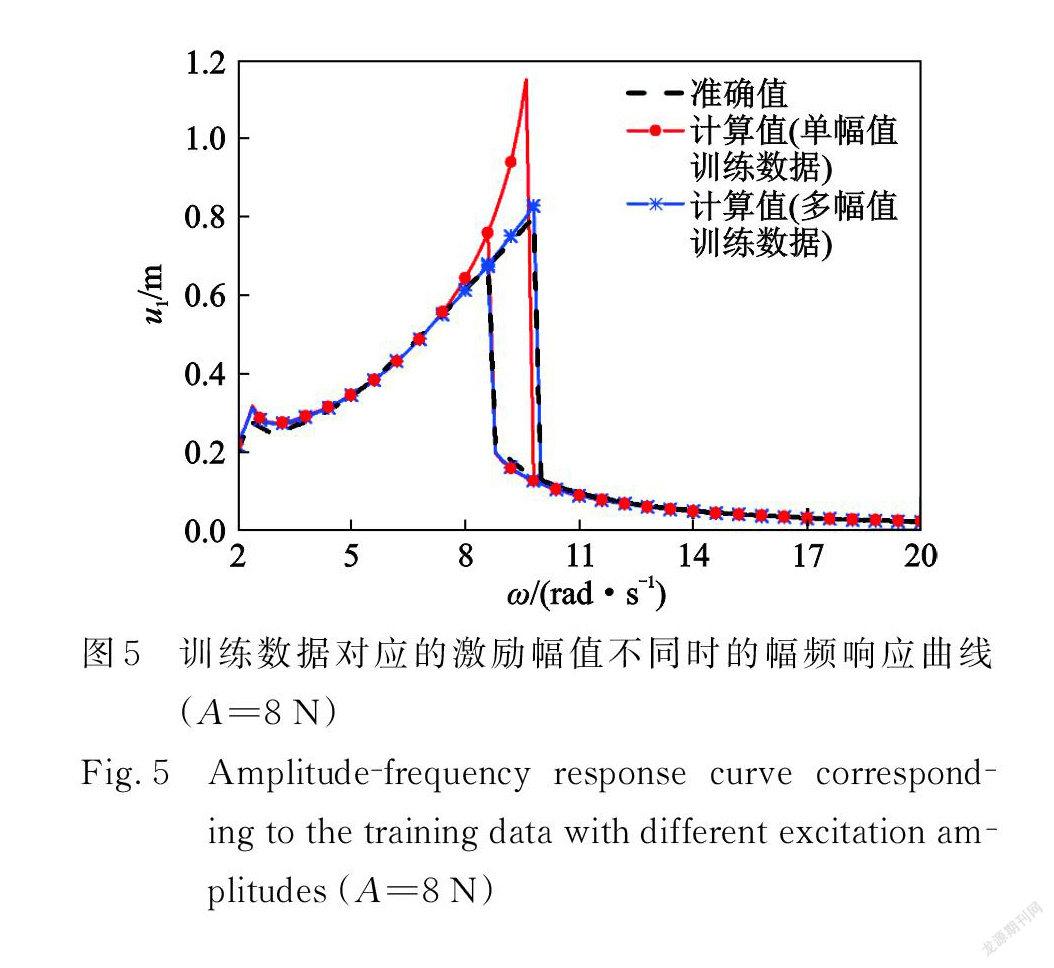
響應預測結果存在誤差的本質是：構建的數據模型與理論模型之間存在差異，兩者不能完全等效替換。究其原因，一是本文側重利用神經網絡進行系統建模和響應預測的流程，神經網絡用了單個隱藏層，網絡結構較簡單，若采用更為復雜的神經網絡結構，有可能提高對理論模型的逼近能力；二是上述算例中選用單一外激勵幅值情況下的響應數據作為網絡訓練數據，訓練數據使用不同激勵幅值下的響應數據，將減小這類響應預測誤差。為驗證響應預測能力與訓練數據對應外激勵幅值的關系，使用外激勵頻率和幅值均變化時的多幅值響應數據，即采集外激勵幅值 A 分別為3，5 N，外激勵頻率ω分別為7，8 rad/s 時的系統時域響應數據。圖 5是訓練數據選用單幅值和多幅值兩種響應數據時的幅頻響應曲線（A=8 N）。結果表明，選用多幅值響應數據進行訓練可以有效提高神經網絡在激勵變化情況時的響應預測能力。

考慮到訓練數據是不同外激勵情況下的系統響應數據，因此外激勵情況將影響訓練數據特征，進而影響網絡的訓練。為探究數據模型精度與訓練數據對應的外激勵頻率的關系，采集外激勵幅值 A=3 N 、激勵頻率ω分別等于6，7，8 rad/s 和5，6，8 rad/ s 的兩組系統時域響應數據，采樣時長0～30 s，采樣頻率100 Hz 。圖6為訓練數據選用不同激勵頻率下的響應數據時的幅頻響應曲線（A=3 N），兩組訓練數據對應的計算值與準確值均基本吻合，且可有效得到系統幅值跳躍時的激勵頻率；同時訓練數據對應的激勵頻率越靠近共振頻率，數據模型的響應預測結果越好。

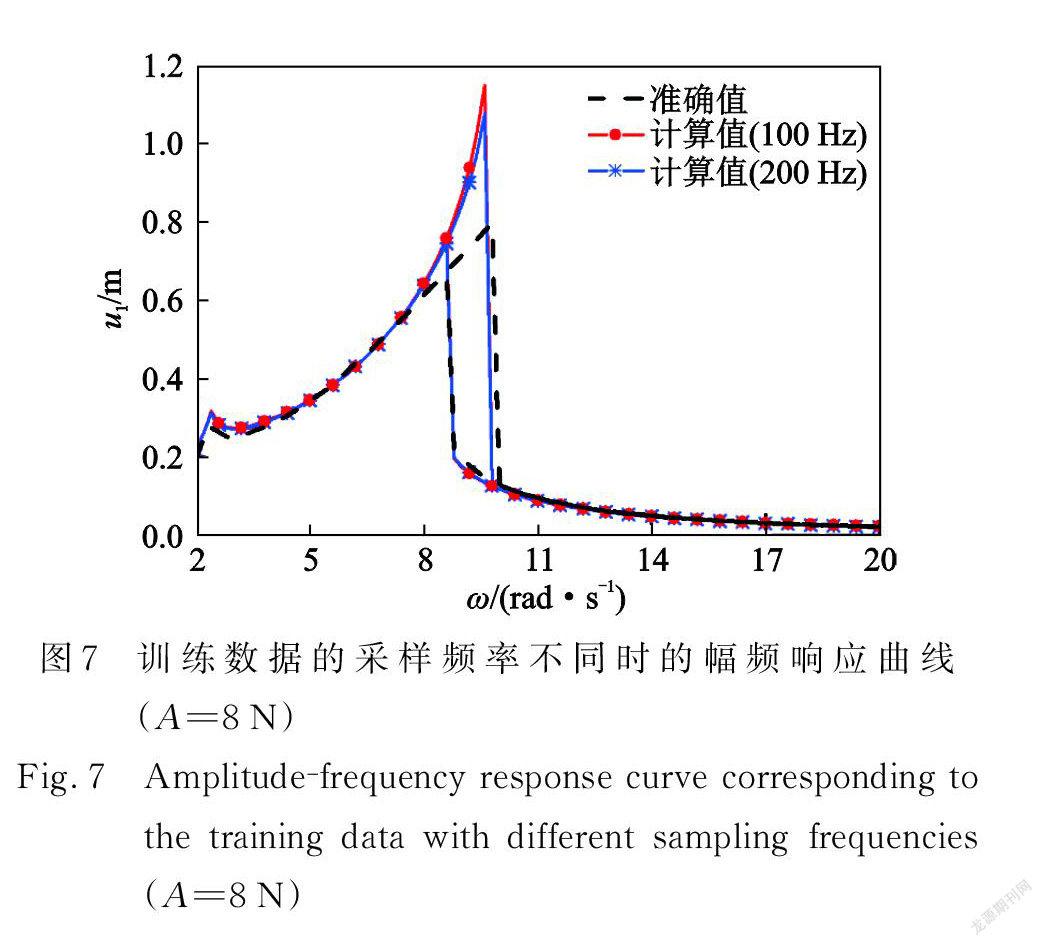
采集系統狀態響應數據時，數據的采樣頻率大小是必要的考慮因素。探究采樣頻率對預測精度的影響，將作為數據獲取時采樣頻率設定的依據。采集外激勵幅值 A=3 N，外激勵頻率ω=6，7，8 rad/s 時的系統時域響應數據，采樣頻率由100 Hz 變為200 Hz 。圖7為由采樣頻率變化前后的訓練數據預測的幅頻響應曲線（A=8 N）。結果表明，采樣頻率滿足采樣定理后，改變采樣頻率對激勵幅值變化時的響應預測能力并沒有明顯增強效果。原因是當改變采樣頻率時，損失函數中數據之間應遵循的動力學規律并沒有很大變化。

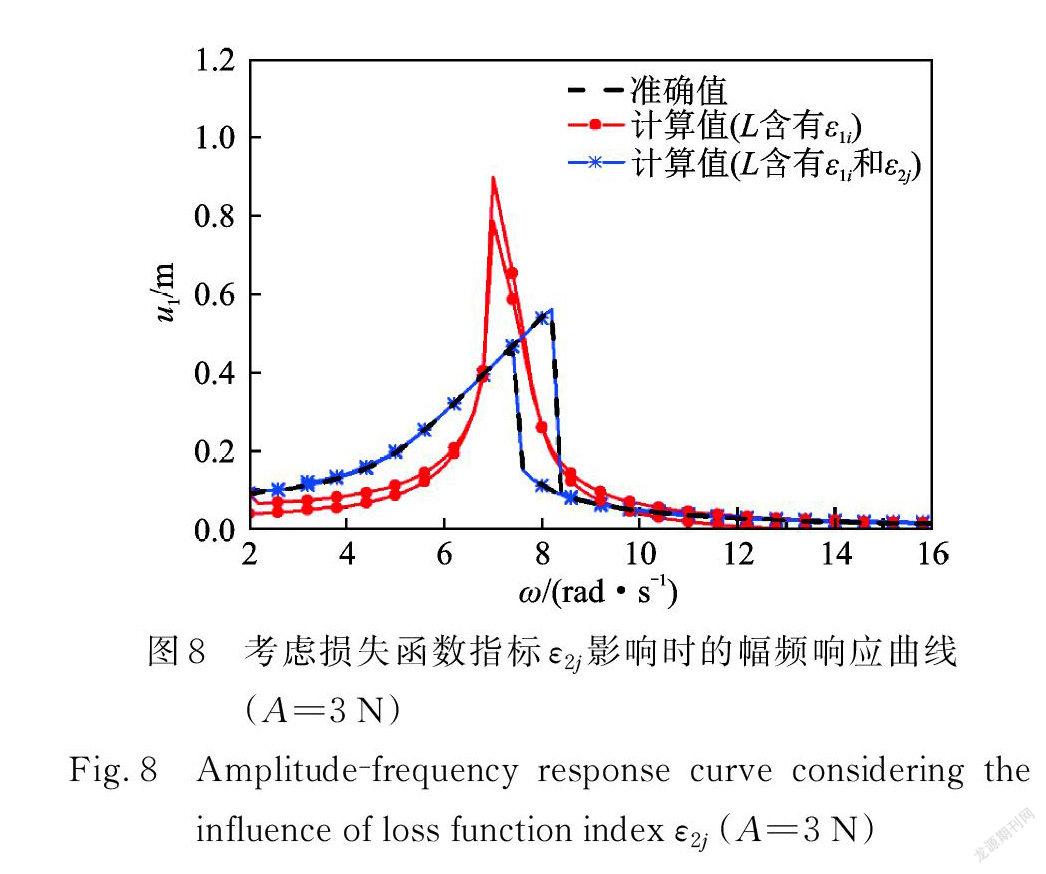
為探究構建損失函數指標 e2j 對提高響應預測能力的有效性，采集外激勵幅值 A=3 N 、外激勵頻率ω=6，7，8 rad/s 的系統時域響應數據，采樣時長0～30 s，采樣頻率100 Hz 。圖8為選取不同損失函數指標時對應的幅頻響應曲線（A=3 N），紅色曲線為損失函數 L 只包含指標 e1i 時的幅頻響應曲線，藍色曲線為 L 包含指標 e1i 和 e2j 時的幅頻響應曲線，前后兩者選用相同的網絡訓練時間。結果表明，在損失函數中補充指標 e2j 能有效地提高數據模型的響應預測能力。

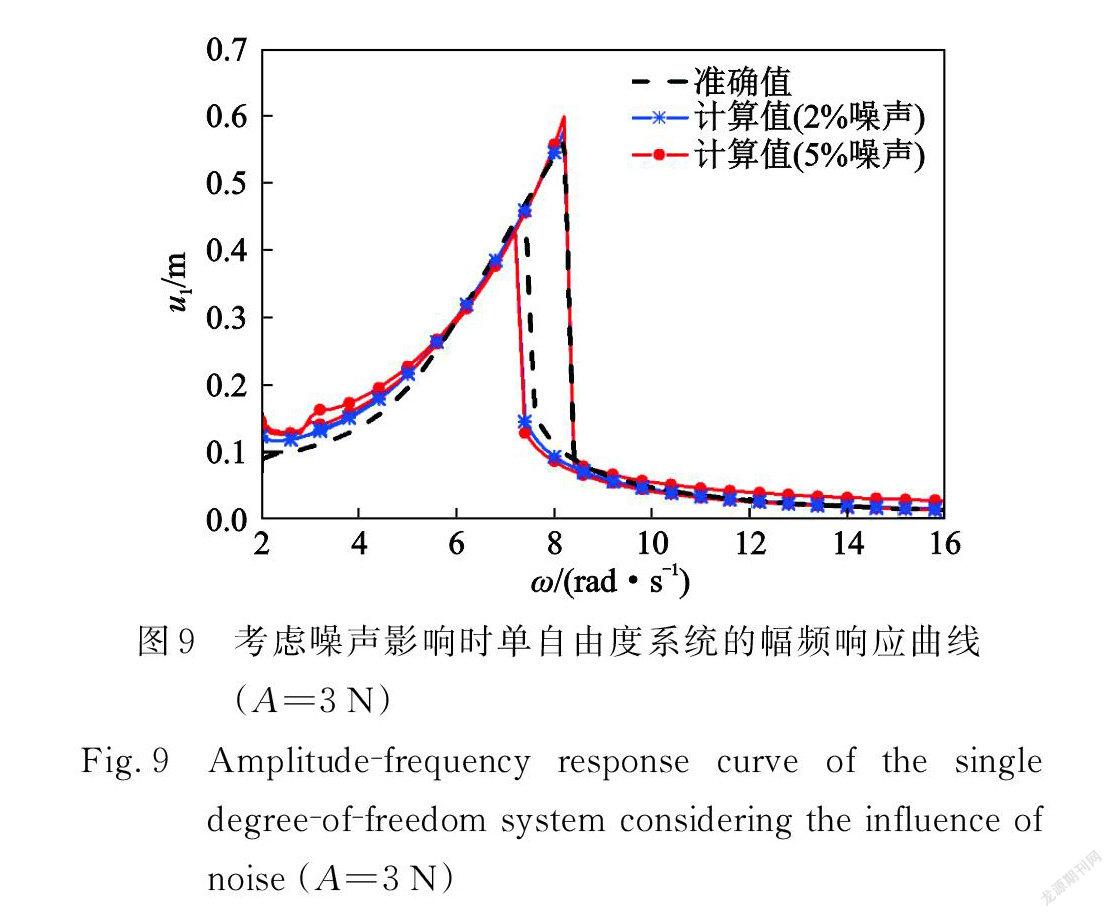
將獨立、同分布的高斯噪聲加到求解方程（11）得到的原始響應數據中，模擬包含環境噪聲的響應數據。噪聲平均幅值為零，標準差分別等于原始響應數據標準差的2%和5%。圖 9考慮了訓練數據中噪聲對響應預測的影響（A=3 N），可以看出預測精度較好，說明所建立的數據模型對噪聲數據有較好魯棒性。

3.2? 間隙非線性的三自由度彈簧質量系統

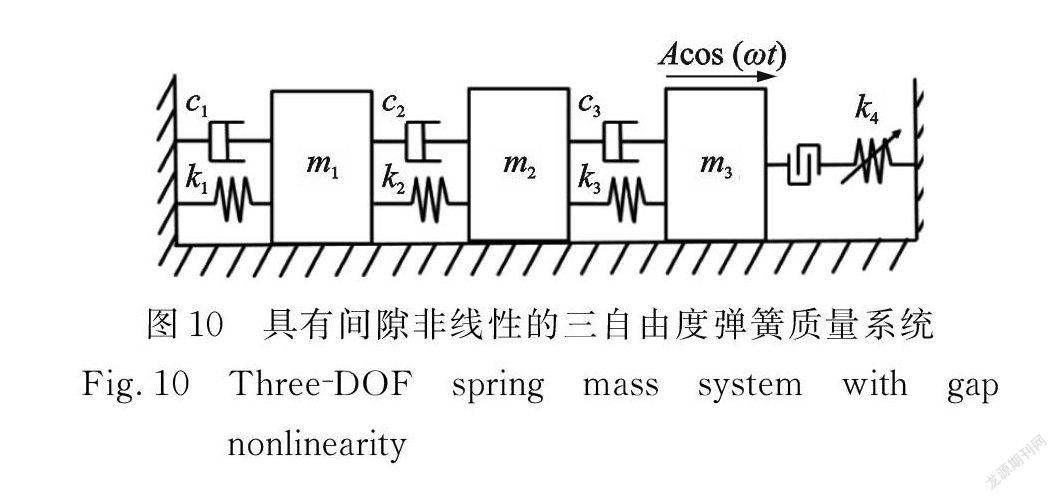
考慮具有間隙非線性的三自由度彈簧質量系統，如圖10所示。

圖10中，k4為立方非線性彈簧，系統動力學方程表示為：

方程（16）中非線性項為：

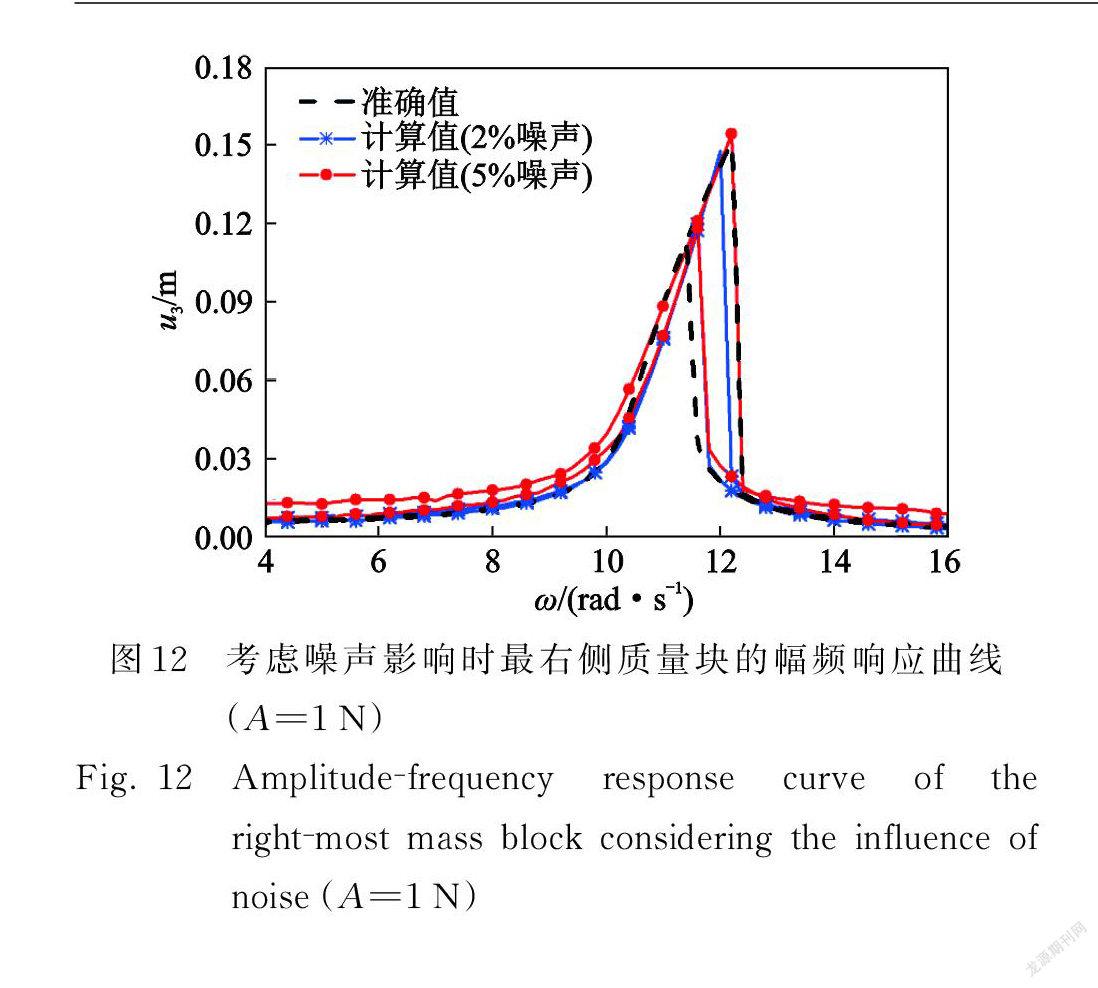
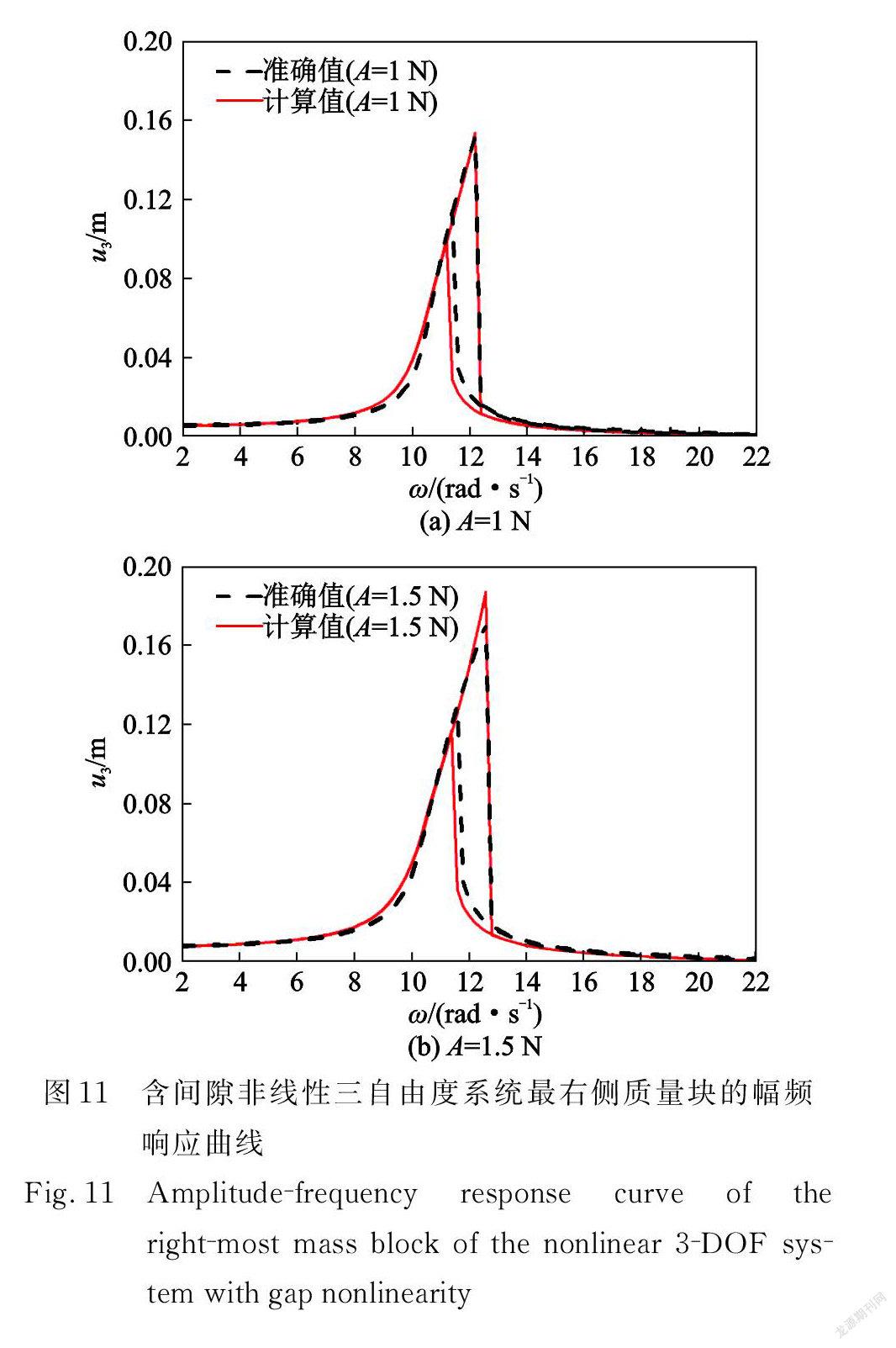
式中δ表示間隙，大小為2 mm 。假設 m 1= m2= m3=1 kg，c1= c2= c3=1 N·s/m，k1= k2= k3=600 N/m，k4=6000 N/m3，第一階無阻尼固有圓頻率為10.9 rad/s 。通過求解動力學方程（16）來模擬外激勵幅值 A=1 N 、外激勵頻率ω=10，11，12rad/s 時的系統時域響應數據的采集，采樣時長0～30 s，采樣頻率100 Hz 。圖11（ a ）為基于數據模型預測的最右側質量塊的幅頻響應曲線（A=1 N）。增大激勵幅值，預測結果仍與準確值基本吻合（圖11（b）為 A=1.5 N 時最右側質量塊的幅頻響應曲線）。結果表明，針對具有間隙非線性的三自由度彈簧質量系統，建立的數據模型能夠有效地計算幅頻響應曲線。

圖12為考慮響應數據中包含噪聲時的幅頻響應曲線（A=1N），可以發現計算值與準確值基本吻合，說明該方法對不同等級噪聲影響下的間隙非線性三自由彈簧質量系統同樣具有較強的魯棒性。

4 結論

本文研究數據驅動的非線性多自由度動力學系統建模和響應預測。通過求解已知狀態方程模擬系統響應數據，并用于訓練神經網絡，然后利用 ODE 求解器進行系統響應預測。依據訓練數據間已知關系構建損失函數，提高了數據模型精度。針對包含立方非線性及間隙非線性的彈簧質量系統進行數值驗證，結果表明：

（1）所提出的方法可根據系統若干外激勵與系統響應數據進行外激勵幅值和頻率變化時的非線性彈簧質量系統響應預測，并進一步獲得系統幅頻響應，同時對訓練數據中的噪聲具有魯棒性。

（2）訓練數據特征對數據模型精度存在影響。訓練數據對應的外激勵頻率越靠近系統共振頻率，數據模型精度越好；使用外激勵幅值不單一的多幅值響應數據進行訓練，可以有效提高數據模型在外激勵幅值變化時的響應預測精度；改變訓練數據的采樣頻率對數據模型精度影響不大。

參考文獻：

[1] 楊強，孟松鶴，仲政，等.力學研究中“大數據”的啟示、應用與挑戰[ J ].力學進展，2020，50（1）：1?44.

Yang Q，Meng S H，Zhong Z，et al . Big Data in me? chanical research：potentials，applications and challeng? es [ J ]. Advances in Mechanics，2020，50（1）：1?44.

[2] 楊衛，趙沛，王宏濤.力學導論[M].北京：科學出版社，2020.

Yang Wei，Zhao Pei，Wang Hongtao . An Overview ofMechanics[M]. Beijing：Science Press，2020.

[3]? Lei Y，Wu Y，Li T . Identification of non?linearstruc?tural parameters under limited input and output measure? ments[ J ]. International Journal of Non?LinearMechan ? ics，2012，47（10）：1141?1146.

[4]? Zhou? S ，Heylen? W ，Sas? P ，et? al . Parametric? modalidentification? of time?varying? structures? and? the? valida? tion approach of modal parameters[ J ]. Mechanical Sys? tems and Signal Processing，2014，47（1?2）：94?119.

[5] 楊智春，丁允停，王樂.用 Padé多項式擬合法辨識動力學系統的物理參數[ J ].振動工程學報，2016，29（1）：24?30.

Yang? Zhichun， Ding? Yunting， Wang? Le . Identifying physical parameters? of structural dynamical? system? us? ingPadé? approximation[ J ]. Journal of Vibration? Engi? neering，2016，29（1）：24?30.

[6]? Lai Z，Nagarajaiah S . Sparse structural system identifi?cation method for nonlinear dynamic systems with hys? teresis/inelastic? behavior [ J ]. Mechanical? Systems? and Signal Processing，2019，117：813?842.

[7] 孫偉，李星占，韓清凱.螺栓聯接梁結構結合部非線性特性參數辨識[ J ].振動工程學報，2013，26（2）：185?191.

Sun? Wei ，Li? Xingzhan，Han? Qingkai . Nonlinear joint parameter? identification? for? bolted? beam? structure [ J ]. Journal? of? Vibration? Engineering ， 2013， 26（2） ：185?191.

[8]? Worden? K ，Staszewski? W? J ， Hensman? J? J . Naturalcomputing? for? mechanical? systems? research ：a? tutorial overview[ J ]. Mechanical? Systems? and? Signal Process? ing，2011，25（1）：4?111.

[9]? Pei J，Smyth A W . New approach to designing multilay?er feedforward neural network architecture for modeling nonlinear restoring? forces . Ⅰ：formulation[ J ]. Journal of Engineering Mechanics，2006，132（12）：1290?1300.

[10] Pei J，Smyth A W . New approach to designing multilay?er feedforward neural network architecture for modeling nonlinear restoring? forces .Ⅱ：applications[ J ]. Journal of Engineering Mechanics，2006，132（12）：1301?1312.

[11] Derkevorkian? A ，Hernandez? Garcia? M ，Yun? H? B ，etal . Nonlinear data ? driven? computational models? for re? sponse? prediction? and? change? detection [ J ]. Structure Control Health Monitoring，2015，22（2）：273?288.

[12] Witters? M ，Swevers? J . Black?box? model? identificationfor?? a?? continuously?? variable ，electro?hydraulicsemi?active damper[ J ]. Mechanical Systems and Signal Processing，2010，24（1）：4?18.

[13] Raissi? M ，Perdikaris? P ，Karniadakis? G? E . Multistepneural? networks? for? data?driven? discovery? of? nonlinear dynamical systems[ J ].2018，arXiv：1801.01236.

[14] Chen T? Q，Rubanova Y，Bettencourt J，et al . Neuralordinary? differential? equations [ J ].? 2018，arXiv：1806.07366.

[15] Raissi?? M ，Perdikaris?? P ，Karniadakis?? G?? E .Physics?informed? neural? networks：a? deep? learning framework for solving forward and inverse problems in? volving nonlinear partial differential equations[ J ]. Jour? nal of Computational Physics，2019，378：686?707.

[16] Wei S，Jin X，Li H . General solutions for nonlinear dif?ferential? equations ：a? rule?basedself?learning? approach using? deep? reinforcement? learning [ J ]. ComputationalMechanics，2019，64（5）：1361?1374.

[17]王高雄，周之銘，朱思銘，等.常微分方程[M].3版.北京：高等教育出版社，2008.

Wang Gaoxiong，Zhou Zhiming，Zhu Siming，et al . Or? dinary? Differential? Equations [M]. 3rd? ed . Beijing： Higher Education Press，2008.

[18] Kingma D P，Ba J . Adam：a method for stochastic opti?mization[ J ].2014，arXiv：1412.6980.

Data ?driven modeling and response prediction of nonlinear multi?degree?of?freedom systems

CAI Jun?tong1，2，YIN Qiang1，2，DING Qian1，2

（1.Department of Mechanics，School of Mechanical Engineeing，Tianjin University，Tianjin 300350，China；

2.Tianjin Key Laboratory of Nonlinear Dynamics and Control，Tianjin 300350，China）

Abstract： Due to the complexity of the engineering system and the uncertainty of the parameters，the dynamic control equations es? tablished by the principles of mechanics are often difficult to meet the requirements of precision . This paper studies data-driven sys? tem modeling and response prediction . First，the numerical solution of the dynamic state equation is used to simulate the system re? sponse under different external excitations measured in the experiment，and the neural network model is trained with the response data . The loss function containing the known relationship between the training data is constructed to improve the accuracy of the neural network，and the data model expressing state relationship is obtained . Then，the neural network model is incorporated into the ordinary differential equation solver to predict the response of the system under different excitations and obtain the amplitude - frequency response relationship . The modeling method is applied to the spring mass system with cubic and gap nonlinearity respec? tively . The calculation results show that an accurate data model can be established based on the response data and the hysteresis and jump responses of the nonlinear system at the main resonance can be obtained . The study also shows that the more the training data has and the more complete the data is，the better the accuracy of the data model and the smaller the error of the predicted re? sponse will be .

Key words ： nonlinear system；data?driven；system modeling；response prediction

作者簡介：蔡君同（1996—），男，碩士研究生。電話：17702299785；E ?mail：cccjuntong@126.com。

通訊作者：丁千（1963—），男，教授。電話：13502119753；E ?mail：qding@tju .edu .cn。