考慮材料參數空間變異性的瀝青混凝土心墻壩?覆蓋層系統地震響應研究

王宗凱 宋志強 劉云賀 王飛

摘要：覆蓋層及壩體材料參數的空間變異性往往顯著影響瀝青混凝土心墻壩?覆蓋層系統的地震響應。提出一種基于數論選點的空間隨機場模擬技術，通過數論選點方法實現隨機點集分布優化，采用正態或對數正態分布函數考慮材料參數空間變異性，采用高斯型自相關函數考慮材料參數空間相關性，通過協方差分解生成隨機參數庫，實現了基于蒙特卡洛法的考慮壩體?覆蓋層材料空間差異性及相關性的隨機場模擬和“非侵入式”隨機有限元計算。以某實際工程為例，選取靜力鄧肯?張 E?B 本構模型和動力等效線性黏彈性本構模型中的敏感參數作為隨機參數，分析了瀝青混凝土心墻壩壩頂、心墻頂水平向峰值加速度和壩體豎向永久變形的均值、變異系數及95%的置信區間限值等統計規律及概率分布檢驗；分析了輸入地震動對隨機響應離散程度和相對于確定值超越概率的影響。結果表明：數論選點法可以顯著優化隨機點集分布和提升計算效率；考慮材料參數的空間隨機性會大概率引起壩體地震響應增大；壩體和覆蓋層材料的空間差異性對壩頂和心墻頂水平峰值加速度的影響大于對永久變形的影響；壩體的地震響應統計結果不一定符合正態或對數正態分布；忽略材料參數的空間變異性會造成瀝青混凝土心墻壩?覆蓋層系統不同工況不同指標地震響應50%～90%概率的低估；覆蓋層地震響應結果的離散程度大于壩體及心墻。

關鍵詞：瀝青混凝土心墻壩；地震響應；覆蓋層；空間變異性；隨機有限元

中圖分類號： TV312??? 文獻標志碼： A??? 文章編號：1004-4523（2022）05-1188-12

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.017

引言

中國西南地區雖然水能資源豐富，但是河床深厚覆蓋層廣泛分布、強震頻發給水電工程的抗震安全帶來嚴峻考驗[1?2]。瀝青混凝土心墻壩由于良好的環境適應能力成為強震區深厚覆蓋層場地的優選壩型，因此開展深厚覆蓋層場地瀝青混凝土心墻壩的抗震安全研究具有十分重要的意義[3]。河床覆蓋層由于類型復雜且結構松散，往往在物理力學性質上呈現出較大的空間變異性和隨機性。對于壩體來說，由于國內外規范對堆石料的級配和母巖性質控制較為“粗獷”[4]以及施工質量控制的不確定性，使得壩體堆石料的物理力學性質也具有一定的空間變異型和隨機性[5]。在以往深厚覆蓋層上瀝青混凝土心墻壩地震響應研究中，往往忽略覆蓋層和壩體材料參數的空間隨機性，使得結構的精確分析所能取得的結果被粗略的經驗指標所覆蓋，難以得出更加符合實際的壩體抗震安全評價結論。

國內外研究者針對材料參數的空間隨機性開展了大量的研究，但多針對于隨機場的生成、模擬方法或者是結構靜力分析，對于材料參數的空間隨機性對結構地震動力響應的影響的研究尚不多見。 Cho[6]和蔣水華等[7]采用 K? L?（KarhuneLoeve?）展開法來進行隨機場的模擬，研究了材料的空間隨機性對邊坡穩定性的影響，但是當研究區域不規則且協方差函數形式復雜時，K ? L 法中的二維 Fredholm 積分方程求解存在一定困難。王建娥等[8]采用 Cho ? lesky分解方法生成了面板堆石壩材料參數的空間隨機場，研究了當考慮材料參數隨機時的面板堆石壩的沉降規律。Suchomel等[9]采用局部平均法模擬了潛在滑動面上的土體參數空間特性，并分析了土體參數空間特性與邊坡失效概率的關系。楊鴿等[10] 采用局部平均細分法模擬面板堆石壩的二維空間隨機場，研究了筑壩堆石料空間不確定性對大壩地震響應的影響。郭晴等[11]假設壩體材料符合特定分布，通過抽樣完成瀝青心墻壩的空間隨機場的生成，并對壩體的應力變形等進行了分析。

以上研究雖然實現了對材料參數的空間變異性及空間隨機場的模擬，針對邊坡、土石壩等分析了結構可靠度、應力變形響應等，得出了一些有價值的研究成果，但是分析時大都采用蒙特卡洛方法進行隨機配點，這種配點方法會給高土石壩工程材料的空間隨機有限元計算帶來較大計算量。同時，針對深厚覆蓋層上瀝青混凝土心墻壩的隨機地震響應研究較少。故本文提出一種基于數論選點的空間隨機場模擬技術，考慮覆蓋層和壩體材料參數的空間隨機性和相關性，開展了瀝青混凝土心墻壩?覆蓋層地震響應隨機有限元計算，得出了壩頂、心墻頂水平向峰值加速度和壩體豎向永久變形的均值、變異系數及95%的置信區間限值等統計規律及概率分布結論；討論了地震動強度對隨機響應離散程度和相對于確定值超越概率的影響，為強震區深厚覆蓋層場地瀝青混凝土心墻土石壩的抗震安全評價提供參考。

1 基于數論選點法空間隨機場模擬

1.1 多維空間變量的數論選點法

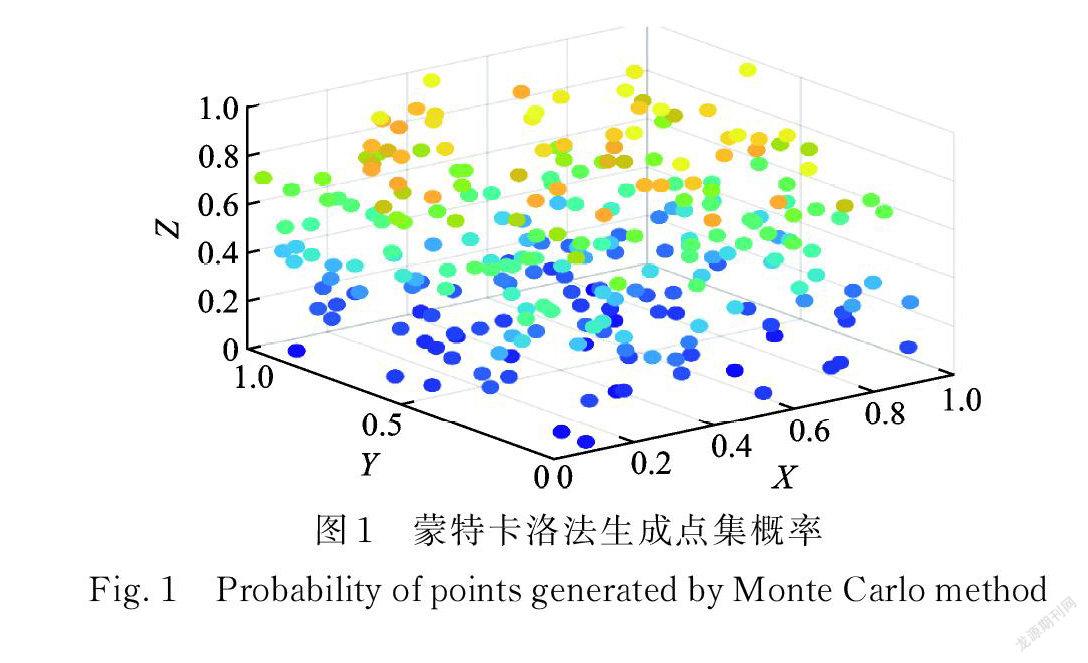
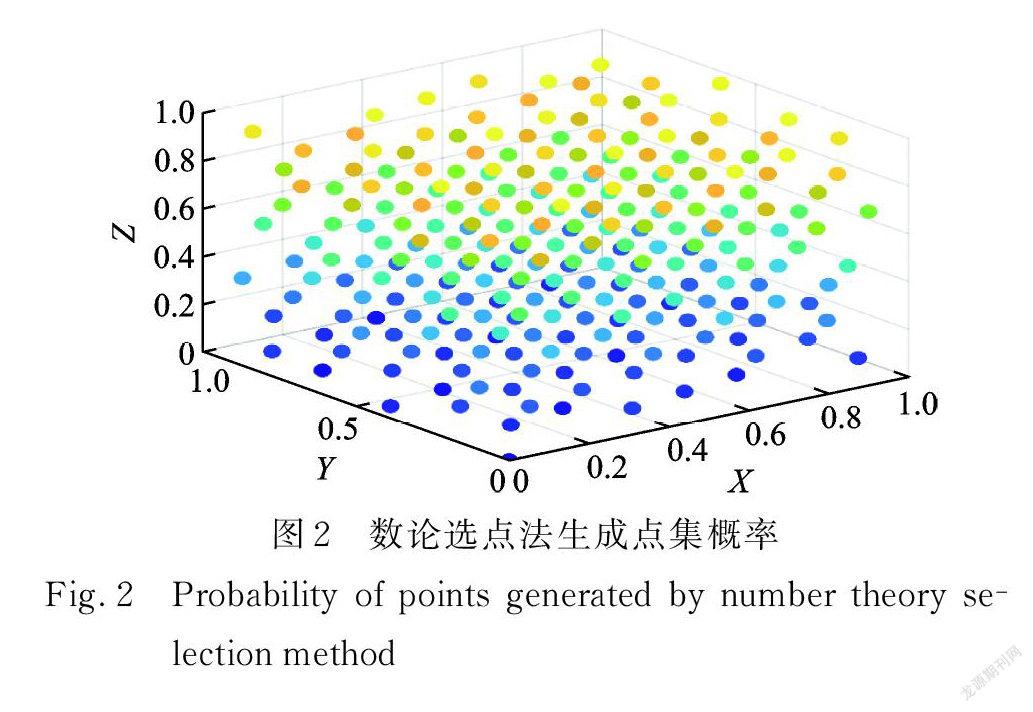
在覆蓋層以及壩體材料的空間變異特性的模擬中，首先需要進行參數的隨機配點，對于空間多維隨機變量問題，傳統蒙特卡洛選點策略產生的樣本點容易出現如圖1所示的局部集中現象，在不增加樣本數量情況下，難以對變量概率分布空間實現全面覆蓋，可能對隨機響應分析結果產生較大偏差[12?13]。如果通過大量增加樣本數量解決該問題，則計算效率顯著下降。

本文將數論方法引入材料參數隨機配點中，該方法能夠實現多維變量概率分布空間的全面均勻覆蓋，與傳統蒙特卡洛配點法相比大幅提升了計算結果的可靠性和計算效率[14]。

多維空間數論選點法的數學理論基礎是華羅庚提出的 Cs 上數論網格[15] ，目前已經被證明 GLP （Good Lattice Point）點集在所有可能生成的點集中具有最小偏差[16]，故本文選擇該點集進行隨機配點的生成。下式給出了 GLP 點集的 s 維生成矢量（N， h1，h2，…，hs ）[13]：

當 z=c 時，函數 H（ z ）在區間1≤z≤（ n-1）/2取得極小值，此時1，c，…，cs-1按模 n 取得最優系數（h1，h2，…，hs ）。文獻[16]中給出了部分最優系數表，可用來產生 GLP 點集。

進一步按照下式可以得到單位超立方立體（0，1） s 內點集xj，k：

1.2 空間隨機場模擬

為了同時考慮材料參數的空間變異性和空間相關性，采用合理的隨機場理論是十分重要的。本文采用中心點離散法分解離散隨機場，通過Nataf逆變換將標準獨立空間的數論點集轉換成符合特定分布的點集，基于 Cholesky 分解法對隨機變量進行變換，結合相關高斯隨機場及對數正態隨機場完成同時考慮差異性和相關性的空間隨機場模擬。隨機場的單元參數通過均值、變異系數、分布函數、相關函數以及相關距離等來進行控制。

中心點離散法取所研究幾何空間域為 V，通過有限元方法離散為 n 個單元體子空間 Vi，即 n 個隨機變量。在二維空間下，子域的中心點記為（Xi， Yi ）。令 H （ X，Y）為空間 V 在力學模型下的參數隨機場，中心點離散法將 Hi （ Xi，Yi ）值賦給子空間 Vi 中心點（Xi，Yi ）來體現該單元子域的材料特征。

由于地基覆蓋層和壩體材料可能的分布類型有多種：如正態分布、對數正態分布、χ2分布、t 分布等。在進行空間隨機場模擬時需要將生成的數論點集xj，k 轉換成符合特定分布的點集，本文采用Nataf逆變換來實現，即對于隨機變量 R 有如下所示的關系：

式中? F-1（·）為分布函數 F（ x ）的反函數，f（x ）為分布函數 F（ x ）的概率密度函數。

通過下式將產生的數論點集xj，k 轉換成符合 F （ x ）分布函數的點集，用來實現對材料參數空間變異性的模擬。

各空間隨機參數的數字特征通過變異系數Cv來描述，變異系數為：

式中σ為各隨機參數標準差；μ為各隨機參數均值。

在覆蓋層及壩體材料參數隨機場的模擬中，一般認為只有在相關距離以內的不同空間點之間的材料特性才會有較強的相關性。本文選用高斯自相關函數計算不同空間點處的相關系數，進而實現對覆蓋層和壩體材料參數的空間相關性的模擬[8]：

為空間中兩點在豎直方向上的距離，τy =| yi - yj |；δh 為水平自相關距離，δ v 為豎直自相關距離，由土體性質進行確定。

通過 Cholesky 分解法使得ρ n × n = Ln × n L n（T）× n，將符合特定分布的點集Aj，k 進行 m 次隨機抽樣生成點數 Am × n，m 為模擬次數，n 為子空間個數。則隨機變量的樣本矩陣 Hm（D）× n 可以通過下式得到：

在計算過程中自相關系數矩陣由于計算誤差或者舍入誤差出現行列式值接近于“0”，此時可以對矩陣進行微調補救，使之可以產生與實際情況相接近的相關系數矩陣[17]。

通過下式便可生成材料參數的非高斯隨機場：

式中μ ln xi，σln xi 分別為第i個變量取對數后的均值和標準差。

2 計算模型及隨機參數

2.1 模型概況

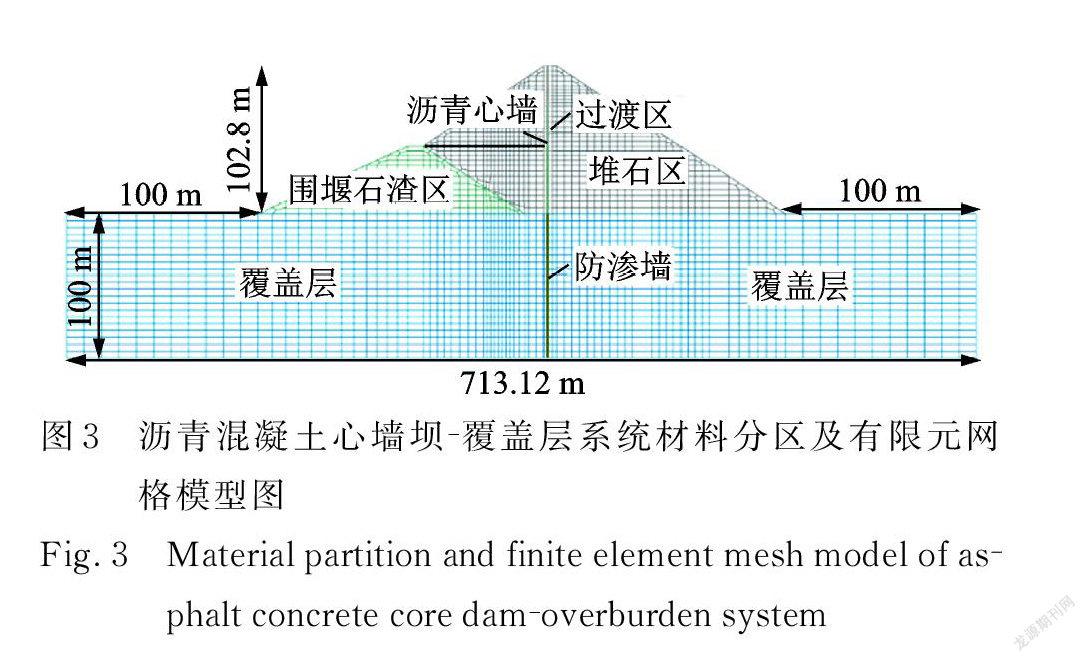
本文選取某實際覆蓋層場地上瀝青混凝土心墻壩為研究對象。最大壩高102.8 m，壩頂寬度10 m，壩頂高程502.8 m，上游壩坡在447.0 m 高程以下為1∶2.5，以上為1∶1.7，下游壩坡為1∶1.7，并在高程467.8 m 和432.8 m 處設置2 m 寬馬道。壩體材料分區如圖3所示，分為堆石區、圍堰石渣區、過渡區、瀝青混凝土心墻以及覆蓋層。利用 ABAQUS 有限元軟件建立瀝青混凝土心墻壩?覆蓋層系統有限元網格模型，單元類型采用四節點等參單元，為了滿足數值計算的要求，有限元模型在進行網格劃分時必須滿足單元長度與寬度小于相關距離，有限元模型網格劃分如圖3所示，共3083個單元，最大網格長度為14.86 m，寬度為4.63 m 。覆蓋層分別向上、下游及深度方向延伸100 m 。靜力計算邊界條件為覆蓋層底部全約束，上、下游兩側的節點在水平方向約束。動力計算將上、下游兩側的節點在水平方向約束，采用一致輸入方法，地震動從覆蓋層底部輸入[18]。 Goodman 接觸單元是一個無厚度的一維單元，由4節點組成。由于其物理意義較為明確且無厚度，可以較好地反映材料性質差異較大的兩種結構接觸面上的張裂和相對滑動，因此在巖土力學中得到了廣泛應用，故對瀝青心墻與過渡料以及防滲墻與覆蓋層之間設置 Goodman 接觸[19]。

2.2? 覆蓋層及壩體材料參數隨機場的建立

瀝青心墻壩的地震響應分析包括靜力計算和動力計算過程，覆蓋層土體和壩體堆石料在靜力計算中采用鄧肯?張 E?B 模型[20]，動力計算采用等效線性黏彈性本構模型[21]，永久變形計算采用等價節點力法和殘余應變模型[21]。

等效線性黏彈性模型假定土料為黏彈性體，通過剪切模量 G 和等效阻尼比λ來表征土體的動應力?應變關系的非線性和滯后性。本文采用沈珠江等建議的形式[21]。

剪切模量：

阻尼比：

應變模型，即沈珠江模型。

動力殘余體積應變增量：

動力殘余剪應變增量：

式中? N 為總振動次數；ΔN 為時段增量； c1，c2，c3，c4，c5為模型參數；S1為應力水平。

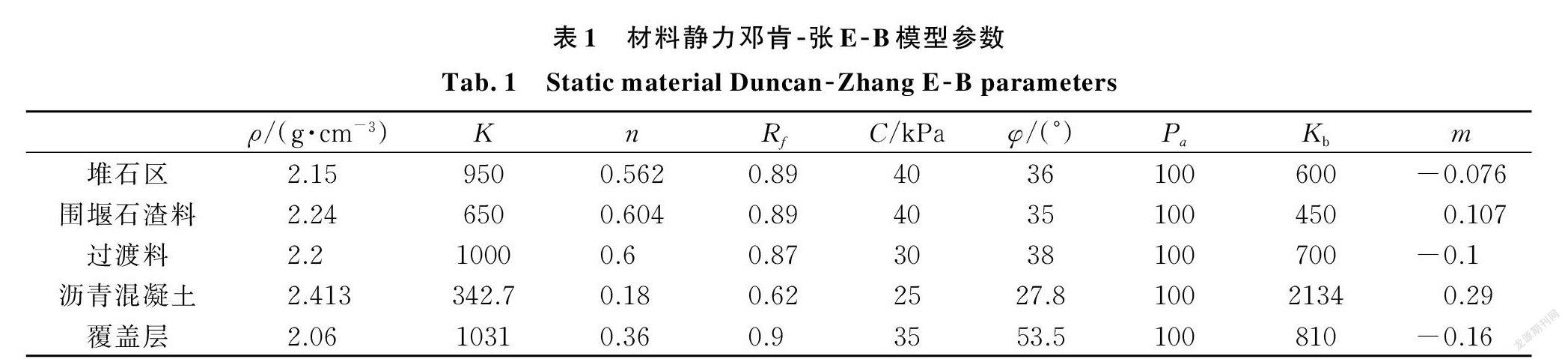
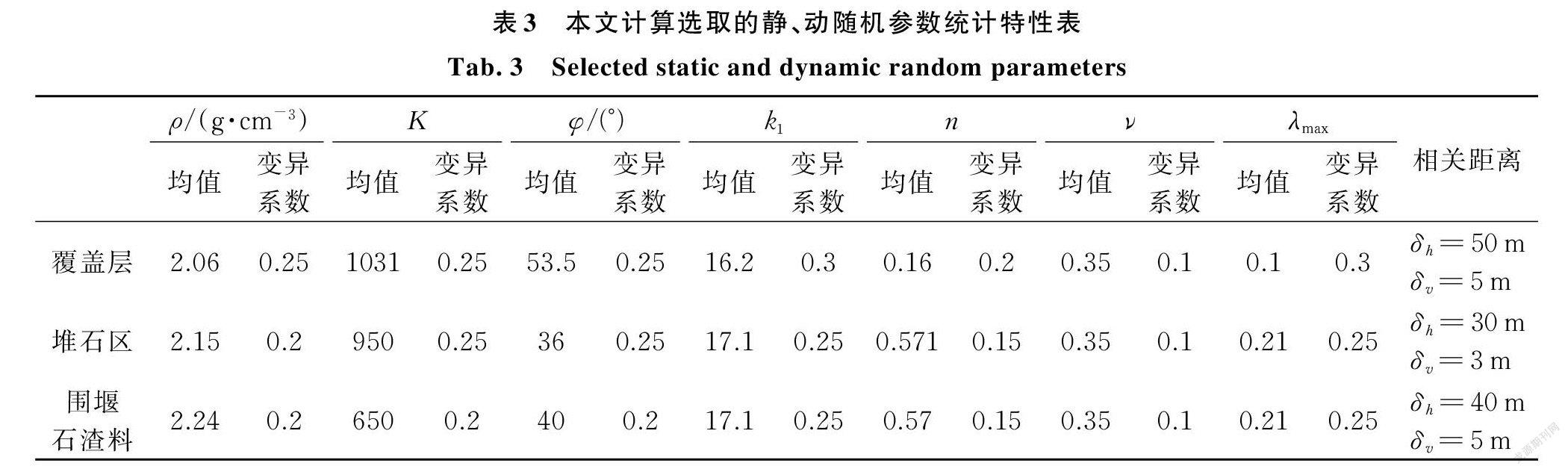
從以上靜、動力本構模型可以看出，反映材料性質的模型參數多達十幾個，如果對每個參數都進行隨機場模擬，會使得計算工作量變得十分龐大，而實際研究發現，不同的參數對計算結果的影響程度不同，僅考慮敏感性較大參數的隨機性，既可以大幅提升計算效率，又可以得到滿足工程精度要求的計算結果。根據以往學者對覆蓋層土體和壩體堆石料靜、動力本構模型參數的敏感性研究結論[22?25]，本文選取靜力參數密度ρ、系數 K 以及摩擦角φ，動力參數 k1，n，ν，λ m ax 作為隨機參數。其他本構模型參數，包括永久變形計算的模型參數取為確定值。表1給出了材料靜力鄧肯?張 E?B 本構模型參數的確定值；表2給出了材料動力等效線性黏彈性本構模型及永久變形計算參數的確定值；表3給出了本文選取的隨機參數的統計分布特性，假設各隨機參數均服從正態分布。

考慮到瀝青混凝土心墻與過渡料由于嚴格的施工控制，其空間特性應該趨于一致，故在隨機場的模擬中對這兩部分材料的參數取確定值。混凝土防滲墻采用線彈性模型計算，彈性模量為28 GPa，泊松比為0.167，密度為2400 kg/m3。

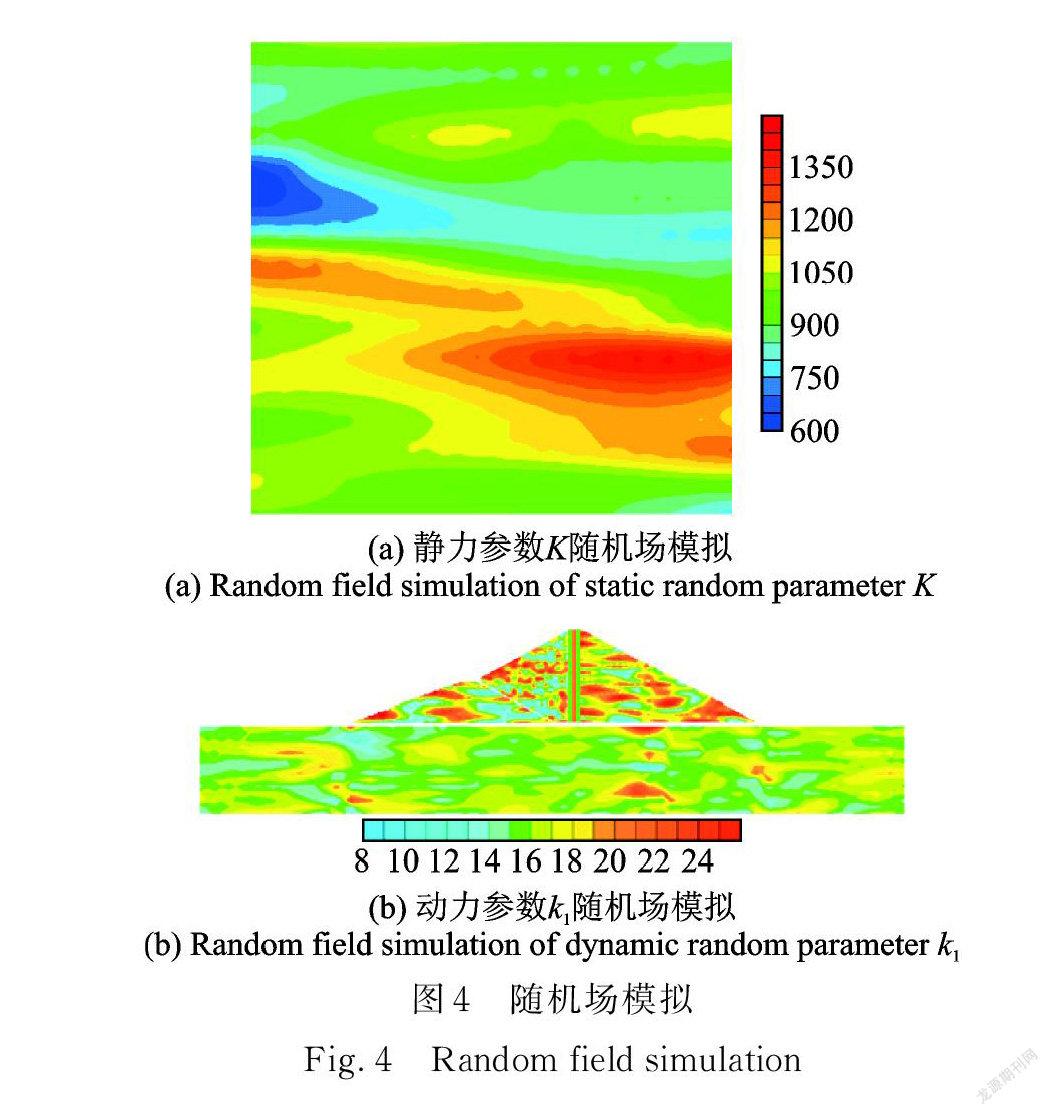
對于覆蓋層、堆石以及圍堰石渣等材料的空間相關性，根據以往學者的分析結論[26]，土體的水平相關距離一般為10～80 m，豎向相關距離一般為1～5 m 。結合本工程的模型信息，本文計算選取相關距離如表3所示。圖 4（ a ）給出了覆蓋層區域靜力隨機參數 K 的隨機場實現云圖，通過40 m×40 m 的網格來進行示意；圖4（b）為考慮材料的空間差異和相關特性后，基于數論選點和 Cholesky 分解方法生成的瀝青混凝土心墻壩?覆蓋層整體模型的材料動力參數 k1非高斯隨機場的一次模擬示意圖。

2.3? 計算流程

本文的計算流程如圖5所示，主要分為三部分：隨機參數庫的生成、隨機有限元分析、計算結果概率統計分析。第一部分，首先通過數論選點法生成隨機變量的多維隨機矩陣，再結合均值、變異系數、相關函數、相關距離等生成材料的隨機參數庫；第二部分，將隨機材料參數賦給有限元模型，在蒙特卡羅法的框架下進行 N 次響應計算，直到計算結果趨于穩定；第三部分，對計算結果進行性態分布、最大值、均值、超標概率等統計分析。

2.4? 計算工況

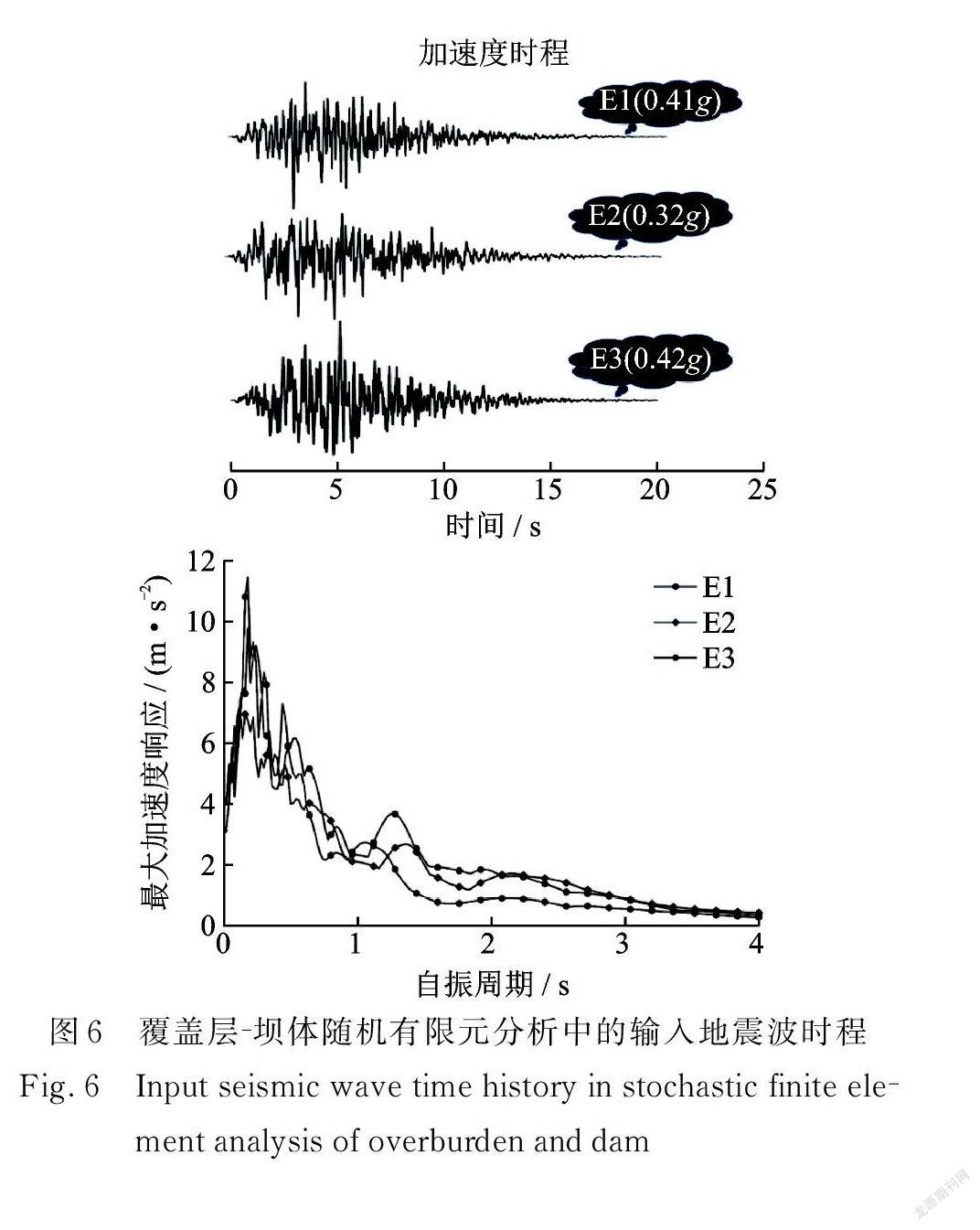
根據某實際瀝青混凝土心墻堆石壩工程所在的場地信息，場地類別為Ⅱ類場地，卓越周期為2.5 s，按水工抗震設計規范標準設計反應譜，生成 E1～E3三條人工地震波作為輸入，地震動水平峰值加速度分別調幅為0.41g，0.32g，0.42g 。地震動輸入采用兩向輸入，持續時間皆為20 s，輸入間隔為0.01 s，豎向峰值加速度取水平向的2/3。圖 6給出了三條人工地震波的加速度時程曲線以及反應譜曲線（阻尼比取為5%）。 E1～E3每條地震波輸入的計算工況分別作為工況1～3，在某一次整體模型靜、動力參數隨機場建立后，分別輸入三條地震波進行三種工況的計算，不同工況進行有限元計算時所對應的模型參數是相同的，這樣可以同時分析在相同材料的空間差異性情況下，不同地震動帶來的影響。

3? 隨機有限元計算結果分析

為了確定計算次數 N 是否足夠，每次計算結束后，將計算的響應結果如壩頂水平加速度、永久變形求平均值，繪制出該平均值隨模擬次數的變化曲線，當所求平均值與上一次誤差小于某收斂閾值即滿足下式時，則證明模擬結果已經達到穩定。

式中μi為第i次計算模擬均值。

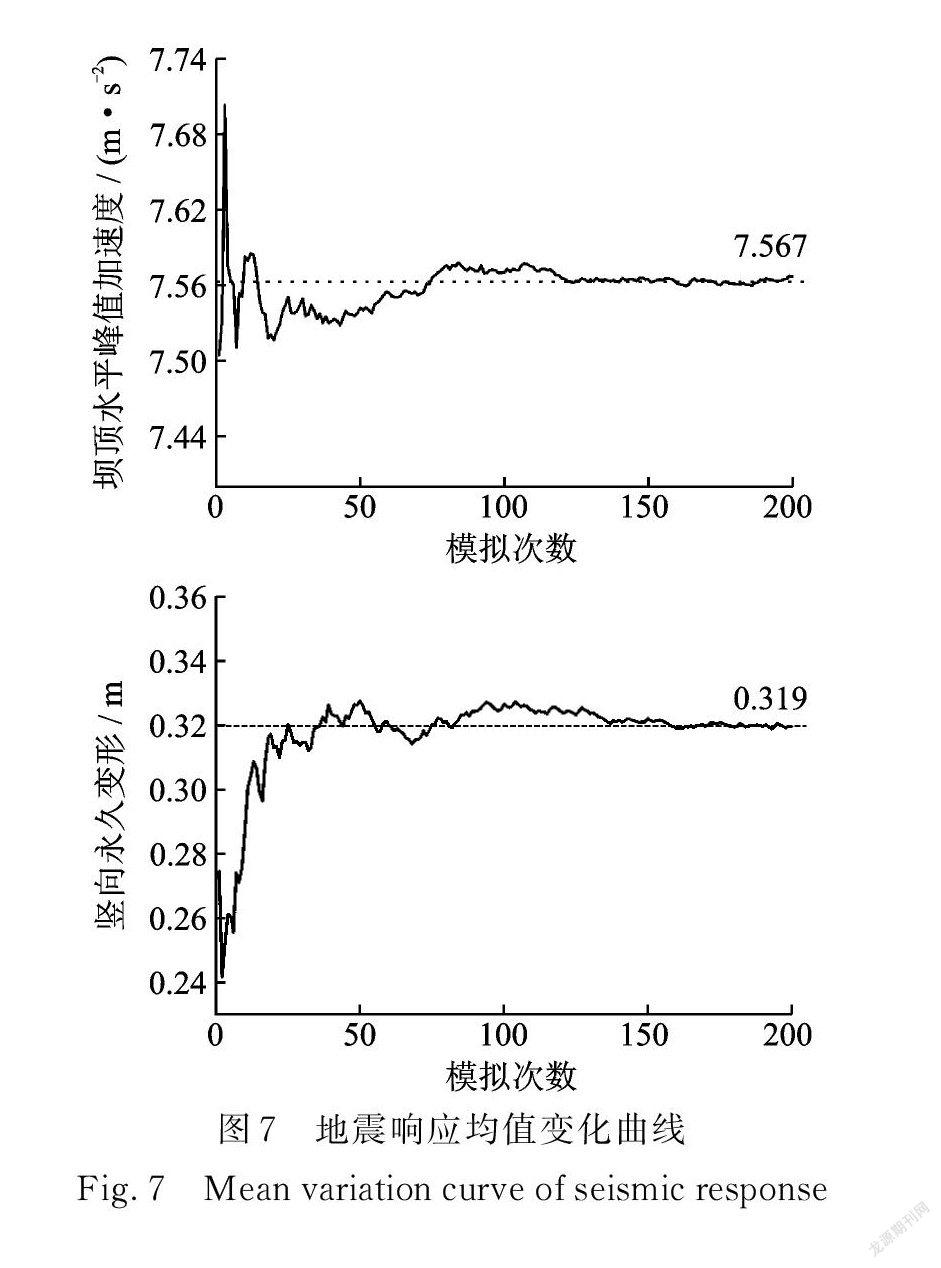
圖7為工況3地震響應均值變化曲線，取 e =0.1%。由圖可見，經73次模擬可以使得計算響應達到穩定值，與傳統蒙特卡羅配點法計算500多次的計算次數相比[27?28]，采用數論選點法進行配點優化大大提高了計算效率。下文將對200次模擬結果進行統計分析，并用樣本去估算總體特性。

3.1? 心墻應力與水平加速度分析

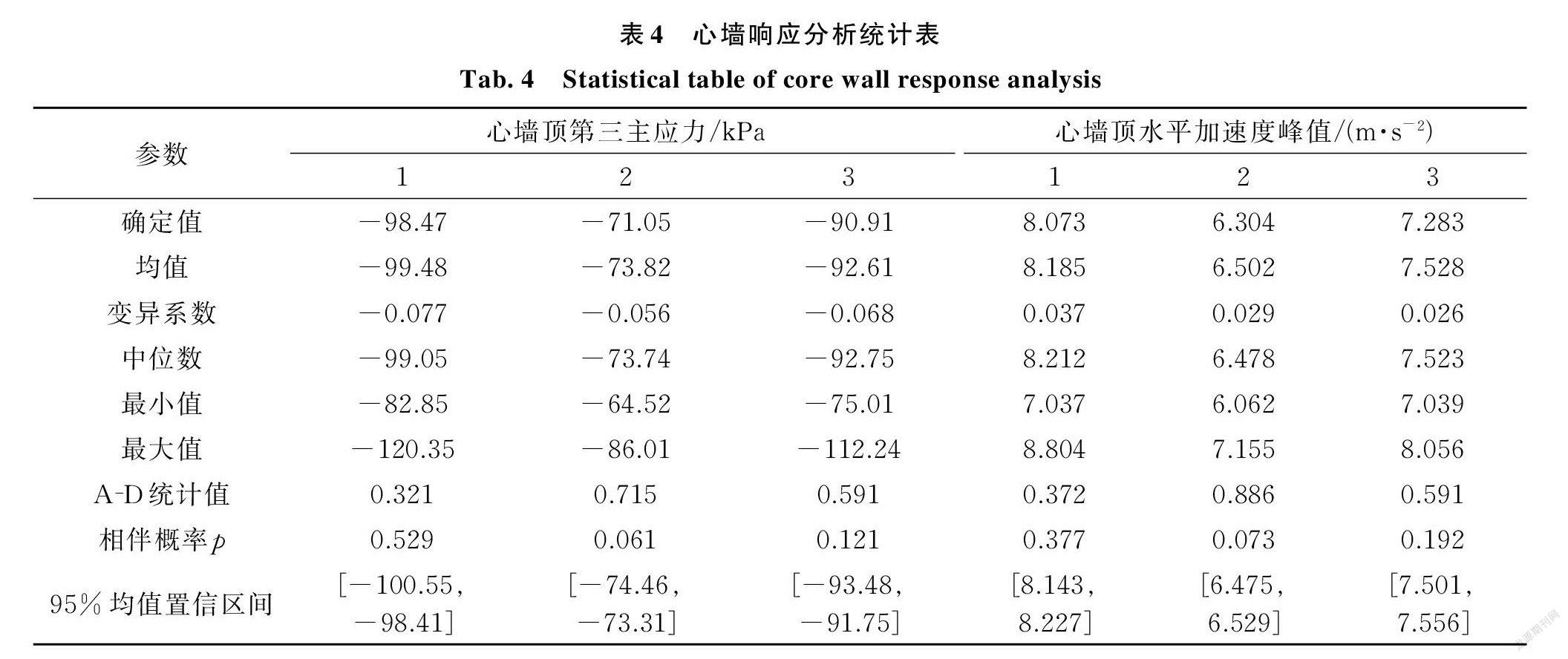
表4為心墻響應統計表，表中的應力值以拉為正、壓為負。從表中可以看到，三種工況下心墻頂處第三主應力確定值的計算結果分別為-98.47，-71.05，-90.91 kPa；當考慮材料空間變異性時，三種工況的均值分別為- 99.48， -73.82，-92.61 kPa，均值結果均大于確定值下的計算結果，最大值分別為-120.35，-86.01，-112.24 kPa，均比確定值計算結果至少增大了20%。對結果進行 A? D 正態分布檢驗，結合統計值與相伴概率可以看出三種工況下考慮材料的空間變異性時，壩肩處心墻的第三主應力均服從正態分布。

從表4可以得到三種工況下心墻頂水平加速度峰值的確定值計算結果分別為8.073，6.304，7.283 m/s2。當考慮材料的空間變異性和相關性后，三種工況下的均值分別為8.185，6.502，7.528 m/s2，均大于確定值的計算結果，并且三種工況下的最大值分別為8.804，7.155，8.056 m/s2，相較于確定值計算結果分別增大9.1%，13.5%和10.6%。經過 A? D 正態分布檢驗可以得出心墻頂水平峰值加速度同樣符合正態分布。

3.2? 壩頂水平加速度分析

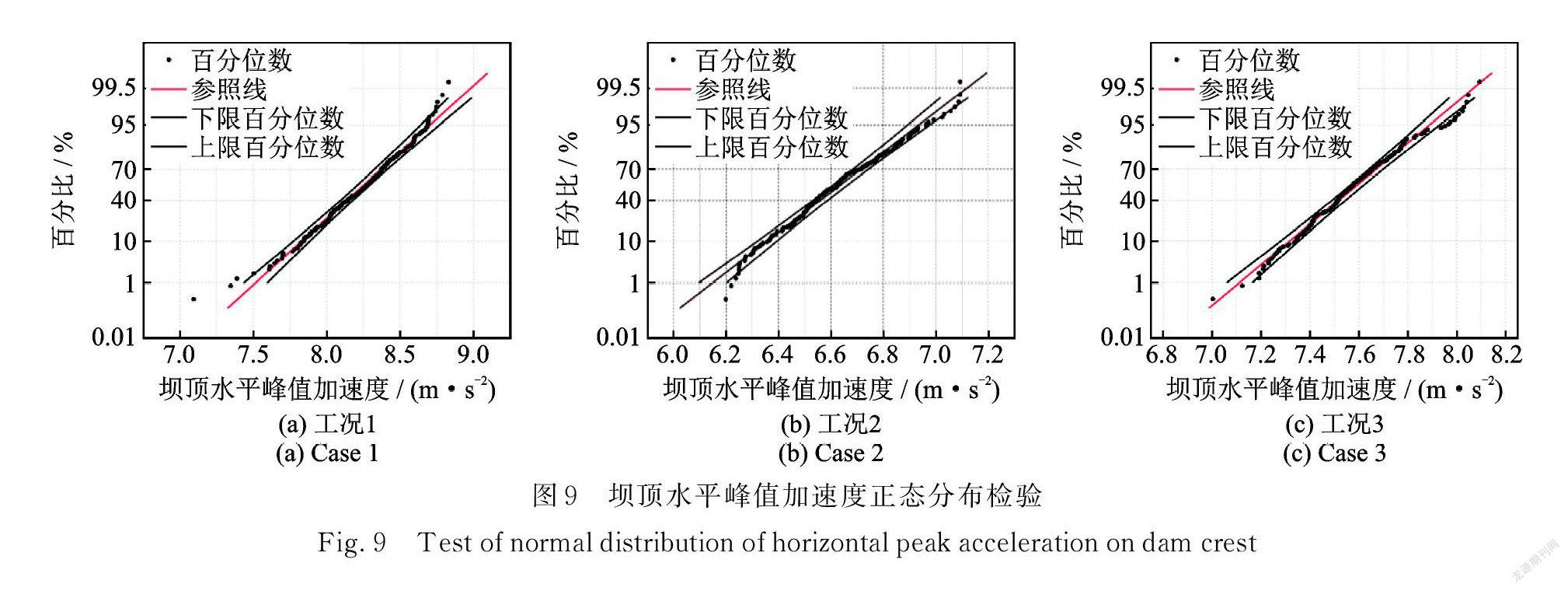
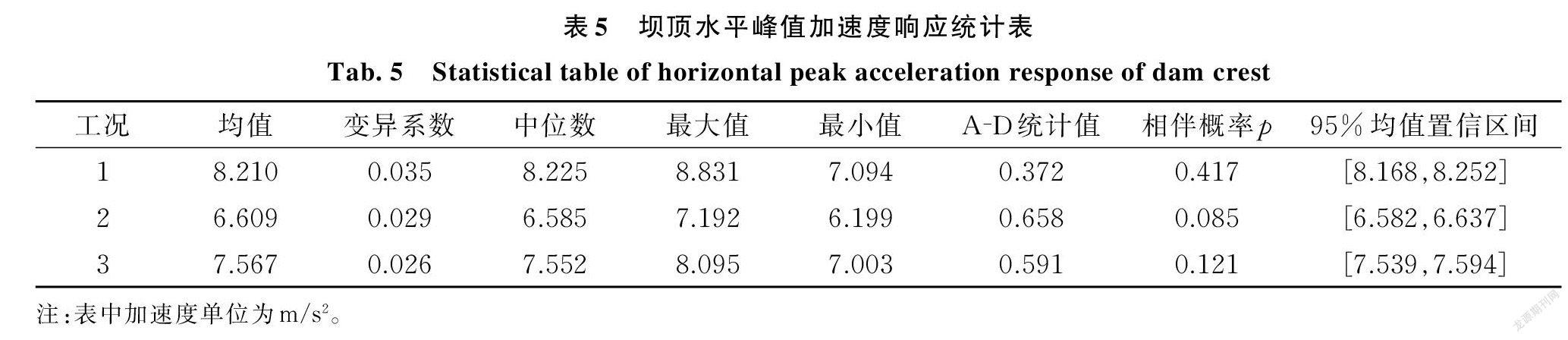
圖8為考慮材料參數的空間變異性的壩頂水平加速度峰值概率分布圖。虛線所示為計算參數取確定值的計算結果，三種工況分別為8.118，6.455，7.364 m/s2。實線所示為考慮材料參數的空間變異性的均值結果，三種工況分別為8.210，6.609，7.567 m/s2，各工況下確定值的計算結果均小于均值結果。對比三種工況的變異系數，工況1最大為3.5%，比工況2和3呈現出更大的離散性。在圖8中可以看到，雖然3種工況下加速度分布的大小不同，但是都呈現出相近的分布規律。圖 9為壩頂水平加速度峰值正態分布檢驗圖，可以看到大多數數據點是集中于參照線附近且在95%置信帶之間。

對數據點進行 A?D 正態分布檢驗結果如表5所示，p 值均大于0.05，故數據結果皆服從于正態分布。

圖10為壩頂水平峰值加速度的含量圖，可以看到三種工況下的最大值分別為8.831，7.192，8.095 m/s2，相較于確定值均增大了9%左右。增大率最大的為工況3，最小為工況2。與確定值相比，三種工況出現了不同的超越概率，最小出現在工況1為62%，最大為工況3達到了87%，即在實際工程地震響應分析中，當不考慮材料參數的空間變異性時，將有60%以上的概率會低估壩頂的水平加速度響應。通過三個工況之間的對比結果可知，考慮材料參數的空間特性差異會使得壩體地震響應相比材料參數取確定值的結果有較大的超越概率，但在不同的工況即不同的地震波作用下，超越概率有較大不同。因此在實際工程中考慮多條地震波輸入情況下研究壩體材料參數的空間變異性響應是很有必要的。

3.3? 壩體豎向永久變形分析

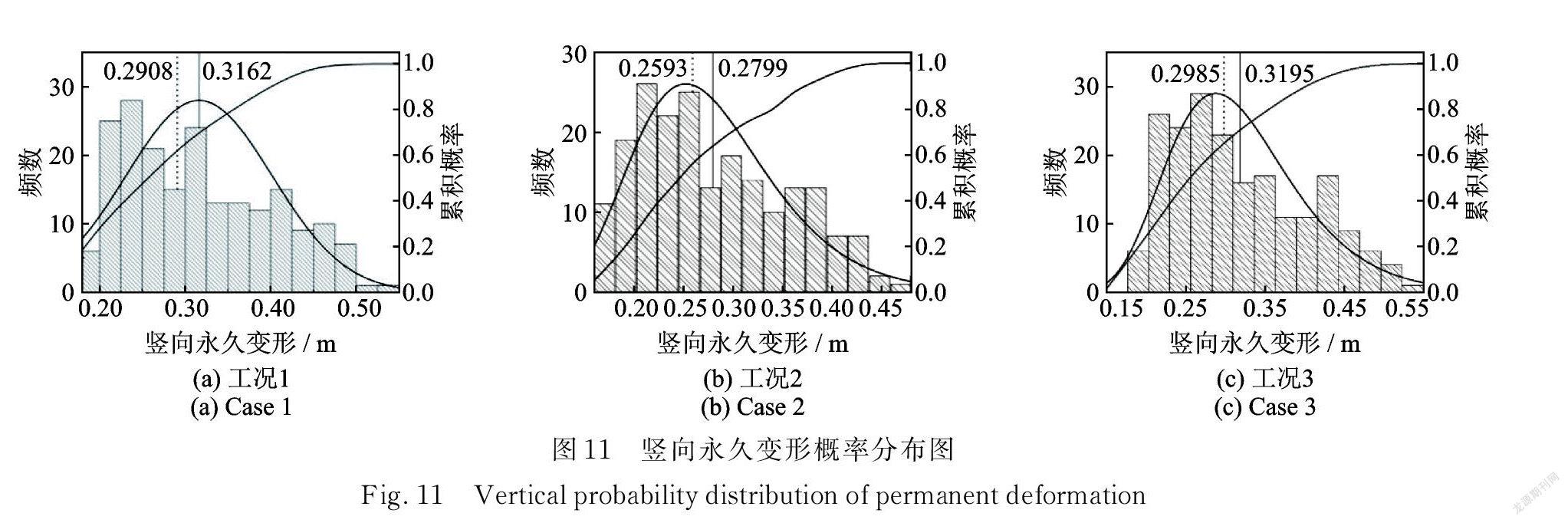
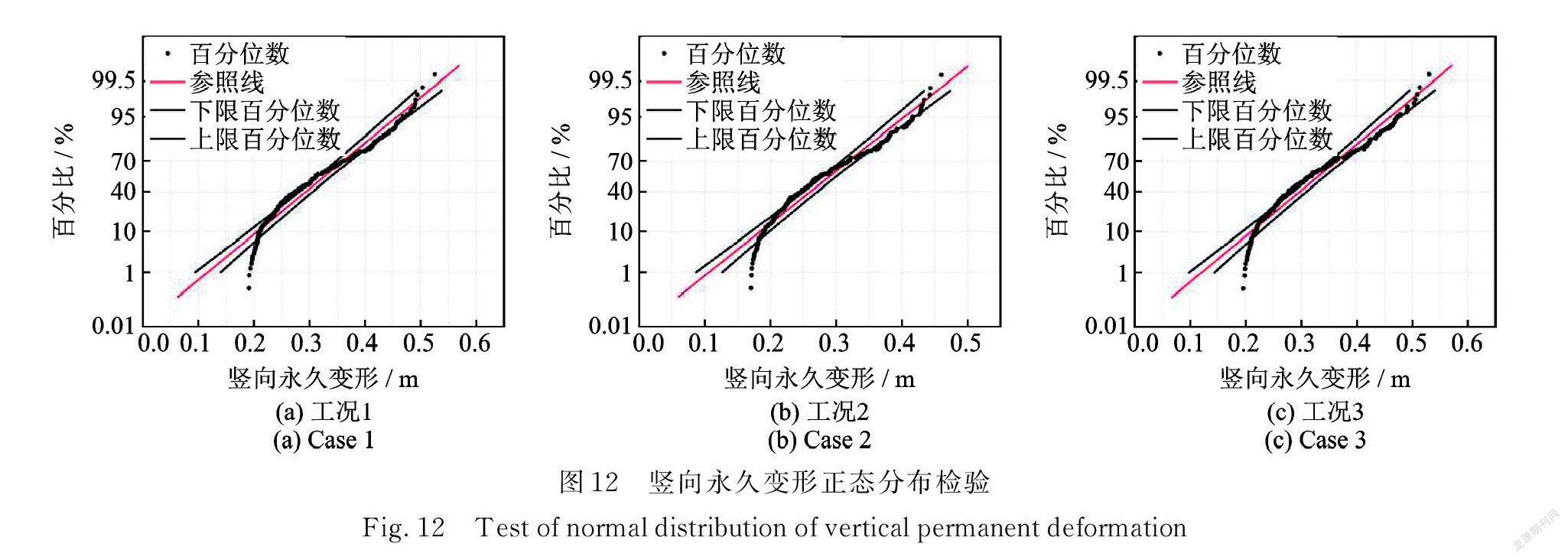
工況下永久變形的確定值計算結果分別為0.2908，0.2593，0.2985 m，考慮材料參數的空間特性時計算結果的均值分別為0.3162，0.2799，0.3195 m 皆大于確定值結果，最大值分別為0.5254，0.4600，0.5303 m，增幅最大的為工況1，為80.6%，最小的為工況2，為77.4%，同時三種工況與確定值相比均有著50%以上的超越概率。與心墻頂及壩頂水平向峰值加速度相比，永久變形的變異系數更大，離散性更強。圖 12為豎向永久變形正態分布檢驗圖，可以看到結果數據與45°直線有較大的偏離，有較多點在95%置信區間以外，并且通過 A?D 正態分布檢驗（如表6所示），豎向永久變形并不符合正態分布。

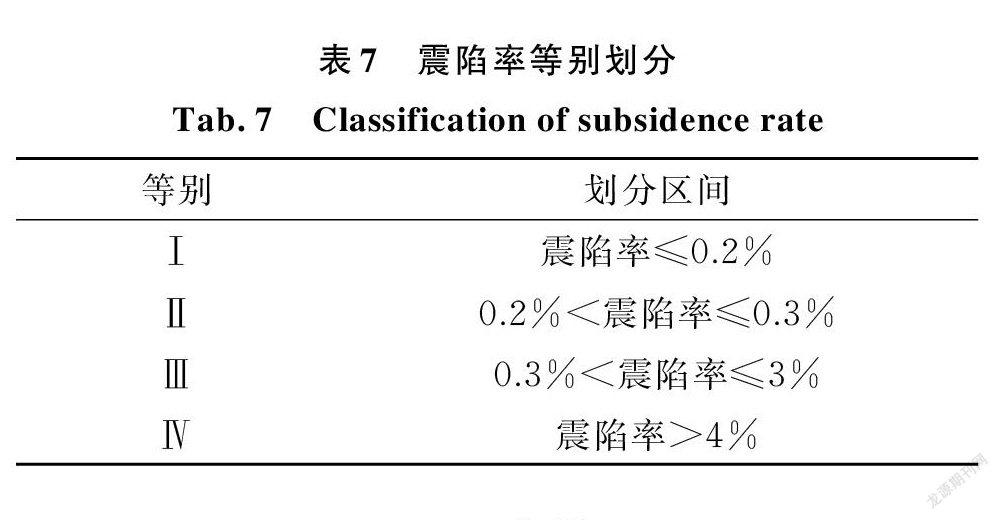
國內一些學者對于高土石壩基于永久變形的極限抗震能力和地震易損性進行研究時，多用壩頂震陷率作為地震變形的控制標準[29?30]，為了使不同隨機有限元計算方法得出的大壩概率安全評價結果之間的比較更有意義，本研究對震陷率進行了等別劃分，如表7所示。按照表7的等別劃分，確定值計算結果均處于第Ⅱ等別，而從圖13中可以看出200次模擬中有40%以上概率震陷率等別大于第Ⅱ等別，達到第Ⅲ甚至第Ⅳ等別，這就使得大壩危險等級顯著提升，如果忽略材料參數的空間特性，將會低估大

3.4? 覆蓋層?壩體沿高度的水平峰值加速度分析

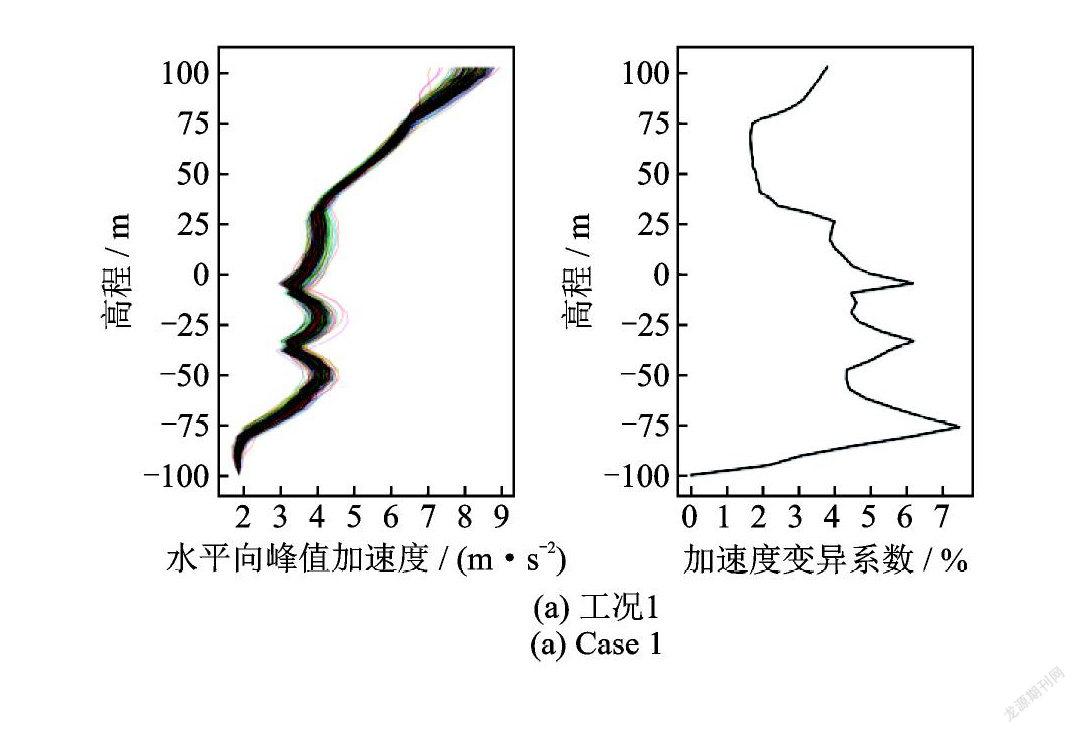
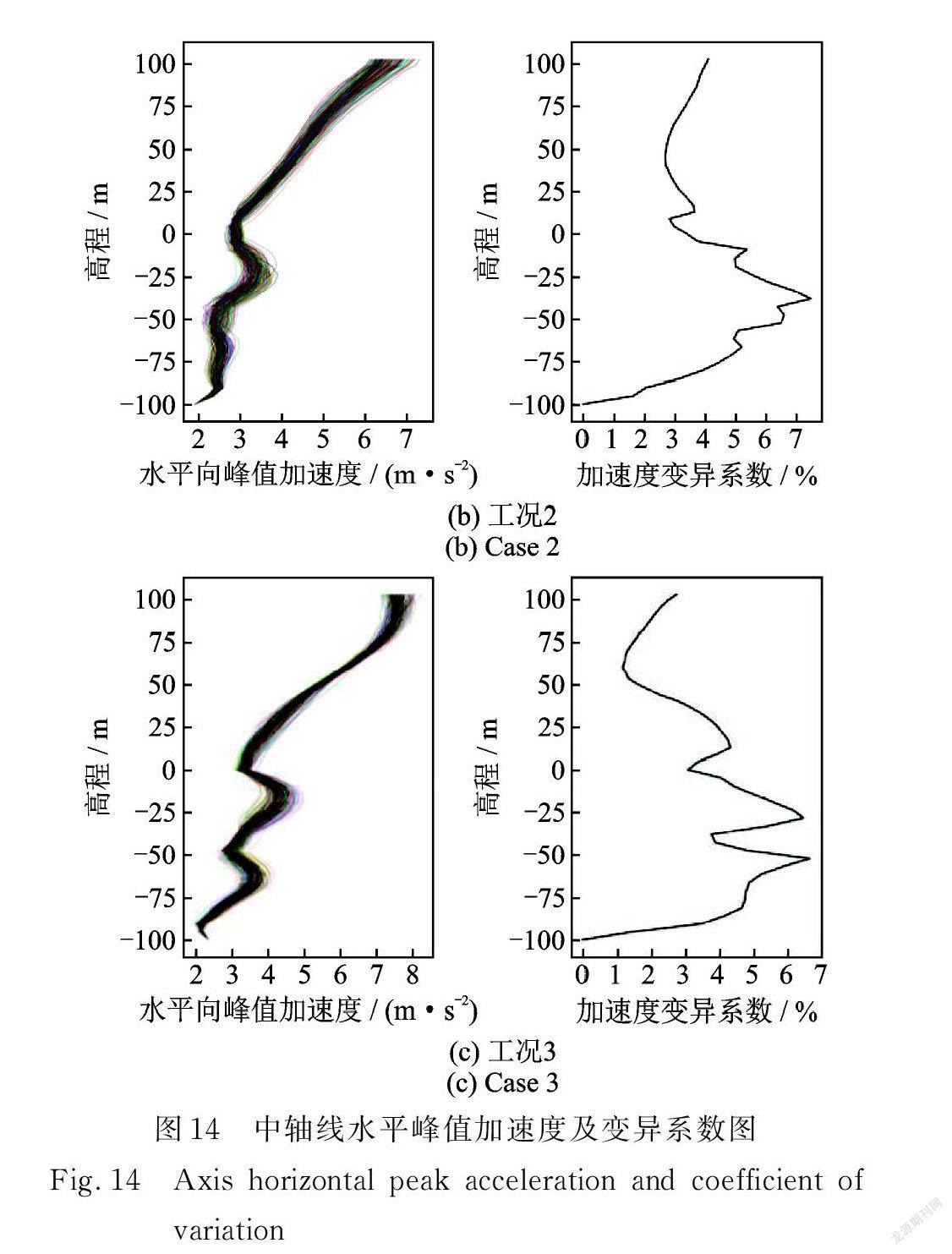
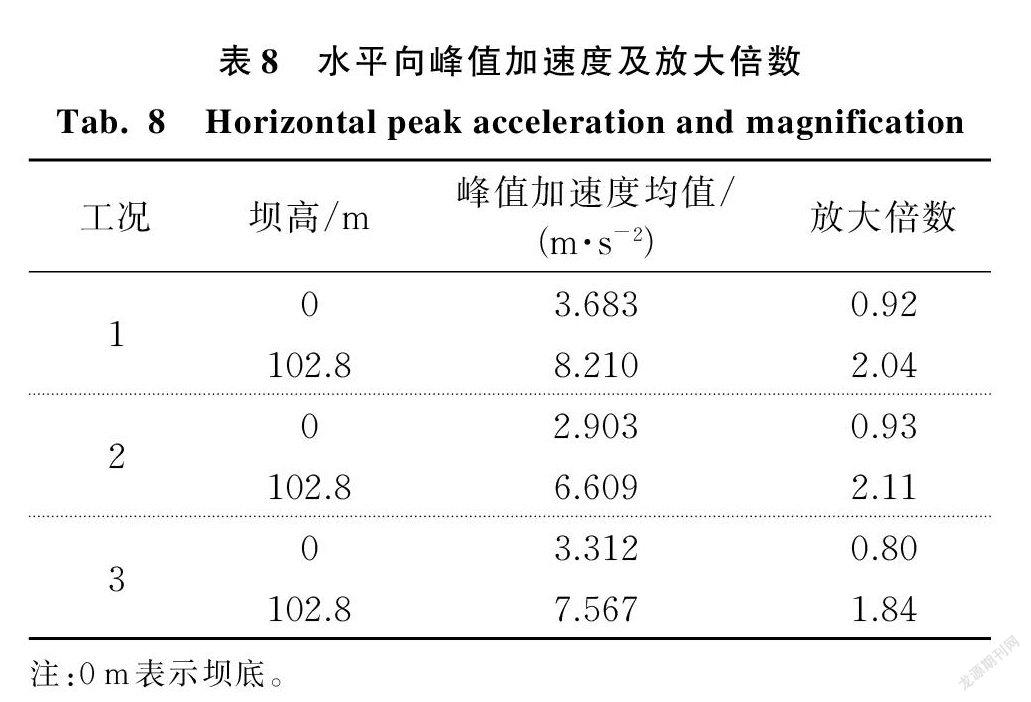
圖14給出了中軸線水平峰值加速度及變異系數圖。從圖中可以看出，考慮材料參數的空間特性時，沿高度的水平峰值加速度覆蓋層處的離散性明顯大于壩體部位，并且兩者之間的變化趨勢呈現出明顯不同的規律，壩體部位隨著高度增大，加速度也在不斷增加，呈近似線性變化，而覆蓋層部位加速度隨高度有增大也有減小，呈非線性變化。對三種工況進行對比可以發現，不同地震動下雖然變化的整體趨勢具有一定的相似性，但是水平向峰值加速度沿高度的變化規律不同；同時通過表8可以看到不同地震動的壩頂峰值加速度放大倍數有著明顯差異。故上述提出在考慮材料參數空間變異性的同時考慮多條地震動對響應的影響是很有必要的。

4 結論

本文提出了基于數論選點優化隨機點集分布的空間隨機場模擬方法，采用正態或對數正態分布函數考慮材料參數的空間變異性，采用高斯型自相關函數考慮材料參數的空間相關性，采用協方差分解生成隨機參數庫，實現了考慮壩體?覆蓋層材料空間差異性及相關性的“非侵入式”隨機有限元計算。以某實際工程為例，選取靜力鄧肯?張 E?B 本構模型和動力等效線性黏彈性本構模型中的敏感參數作為隨機參數，分析瀝青混凝土心墻壩壩頂、心墻頂水平向峰值加速度和壩體豎向永久變形的均值、變異系數及95%的置信區間限值等統計規律及概率分布檢驗；分析了輸入地震動強度對隨機響應離散程度和相對于確定值的超越概率的影響。具體結論如下：

（1）與傳統蒙特卡洛隨機點生成方法相比，數論選點法可以實現對多維變量概率分布空間的全覆蓋，在精度不受影響的前提下，大大減少有限元計算次數，顯著提升多維隨機空間模擬和隨機有限元計算效率。

（2）在三種工況下的隨機有限元計算結果中，地震響應的統計結果有40%～90%的概率會超出參數確定下的計算結果，這表示忽略材料的空間變異性可能導致低估大壩的地震響應：心墻頂處的第三主應力最大值超出確定性參數結果20%以上，壩頂水平峰值加速度最大值超出確定參數結果的9.9%，各地震工況下結果相比確定參數結果超越概率在62.5%～87%之間；心墻頂部峰值加速度最大值超出確定參數結果13.5%；豎向永久變形最大值超出確定參數結果的80.6%，各地震工況的超越概率均在50%以上。

（3）壩體和覆蓋層材料參數的不確定性使得結構動力響應的結果發生離散，隨機有限元計算的統計結果中壩頂和心墻頂水平加速度結果符合正態分布，豎向永久變形結果則不符合。對于覆蓋層?壩體系統中軸線的水平向峰值加速度，覆蓋層中軸線的變異系數最大為7.4%，心墻中軸線的變異系數最大為4.3%，這表明盡管同時考慮了覆蓋層和壩體材料的空間隨機性，但隨機響應結果的離散仍是在覆蓋層地基區域更為顯著。

（4）不同地震工況下水平峰值加速度沿高度的變化規律有較大的區別，加速度放大倍數也有顯著差異，說明地震動差異帶來的影響也是不可忽略的，應同時考慮材料參數的空間變異性和地震動的隨機性進行瀝青混凝土心墻壩?覆蓋層系統的地震響應分析，以得到更加符合實際情況的壩體響應結果和抗震安全評價結論。

參考文獻：

[1] 鄒德高，余翔，余挺，等.深厚覆蓋層上高土石壩動力穩定分析[ J ].水電與抽水蓄能，2020，6（1）：22-27.

ZOU Degao，YU Xiang，YU Ting，et al . Study on the dynamic stability analysis method for high earth built on deep? overburden [ J ]. Hydropower? and? Pumped? Stor? age，2020，6（1）：22-27.

[2] 孔憲京，陳健云，鄒德高.高壩抗震安全理論發展趨勢研究[ J ].水力發電學報，2020，39（7）：1-11.

KONG? Xianjing，CHEN? Jianyun，ZOU? Degao . Study on development trend? of seismic? safety theory? for high dams[ J ]. Journal of Hydroelectric Engineering ，2020，39（7）：1-11.

[3] 劉升歡，宋志強，王飛，等.深厚覆蓋層液化對場地卓越周期及土石壩地震響應影響研究[ J ].振動工程學報，2021，34（4）：721-729.

LIU? Shenghuan，SONG Zhiqiang，WANG Fei，et al . Influence of liquefaction of deep overburden on the site predominant? period? and? seismic? response? of the? earth- rock dam[ J ]. ，2021，34（4）：721-729.

[4] 水工建筑物抗震設計標準：GB 521247—2018[S].北京：中國計劃出版社，2018.

Standard for seismic design of hydraulic structures：GB 521247—2018[S]. Beijing： China? Planning? Press，2018.

[5] 林威偉，鐘登華，胡煒，等，基于隨機森林算法的土石壩壓實質量動態評價研究[ J ].水利學報，2018，49（8）：945-955.

LIN? Weiwei ， ZHONG? Denghua， HU? Wei ， et? al . Study? on? dynamic? evaluation? of? compaction? quality? of earth rock dam based on Random Forest[ J ]. Journal of Hydraulic Engineering，2018，49（8）：945-955.

[6]? Cho S E . Probabilistic assessment of slope stability thatconsiders? the? spatial? variability? of? soil? properties [ J ]. Journal? of? Geotechnical? and? Geo-environmental? Engi? neering，ASCE，2010，136（7）：975-984.

[7] 蔣水華，劉賢，黃勁松，等.考慮水力模型參數空間變異性土石壩邊坡可靠度分析[ J ].應用基礎與工程科學學報，2021，29（4）：939-951.

JIANG? Shuihua，LIU? Xian ，HUANG? Jinsong，et? al . Reliability? analysis? of? slope? stability? of? embankment dams? considering? spatial? variability? of hydraulic? model parameters [ J ]. Journal of Basic Science and Engineer? ing，2021，29（4）：939-951.

[8] 王建娥，楊杰，程琳，等.考慮材料參數空間變異性的堆石壩非侵入式隨機有限元研究[ J ].水資源與水工程學報，2019，30（3）：200-207.

WANG? Jiane，YANG? Jie，CHENG? Lin，et al . Study on? the? noninvasive? stochastic? finite? element? method? of rockfill dam considering spatial variability of material pa? rameters[ J ] Journal of Water Resources and Water En ? gineering，2019，30（3）：200-207.

[9]? Suchomel R，Masion D . Comparison of different proba?

bilitymethods? for predicting? stability? of a slope in? spa? tially? variable? c-soil [ J ]. Computers? and? Geotechnics，2010，37（1）：132-140.

[10]楊鴿，朱晟.考慮堆石料空間變異性的土石壩地震反應隨機有限元分析[ J ].巖土工程學報，2016，38（10）：1822-1832.

YANG? Ge ，ZHU? Sheng . Seismic? response? of rockfill dams considering spatial variability of rockfill? materials via random? finite element method [ J ]. Chinese Journalof? Geotechnical? Engineering ，2016，38（10）： 1822-1832.

[11]郭晴，劉東海，陳輝.空間差異性下瀝青混凝土心墻壩應力與變形的隨機有限元分析[ J ].長江科學院院報，2019，36（11）：140-146.

GUO Qing，LIU Donghai，CHEN Hui . Stress and de ? formation of asphalt concrete core wall dam in consider? ation of spatial difference：stochastic finite element anal? ysis[ J ]. Journal of Yangtze River Scientific Research In? stitute，2019，36（11）：140-146.

[12]陳建兵，李杰.結構隨機響應概率密度演化分析的數論選點法[ J ].力學學報，2006，38（1）：134-140.

CHEN Jianbing，Li Jie . Strategy of selecting points via number theoretical method in probability evolution anal? ysis of stochastic response of structure[ J ]. Chinese Jour? nal? of? Theoretical? and? Applied? Mechanics，2006，38（1）：134-140.

[13] Li? J ，Chen? J . Stochastic? Dynamics? of Structures [M].John Wiley & Sons，2009.

[14]華羅庚，王元.數論在近似分析中的應用[M].北京：科學出版社，1978.

HUA Luogeng，WANG Yuan . Application of Number Theory in Approximate Analysis[M]. Beijing：Science Press，1978.

[15]汪新槐.多維數值積分的數論方法及其在結構可靠度分析中的應用[ D ].南京：河海大學，2005.

WANG Xinhuai . Number theoretical Method for numer? ical multiple integrals and the application in structural re? liability analysis[ D ]. Nanjing：Hohai University，2005.

[16]方開泰，王元.數論方法在統計中的應用[M].北京：科學出版社，1996.

FANG Kaitai，WANG Yuan . Number-theoretic Meth ? ods? in? Statistics? Chapman? and? Hall[M]. Beijing ：Sci? ence Press，1996.

[17]文德智，卓仁鴻，丁大杰，等.蒙特卡羅模擬中相關變量隨機數序列的產生方法[ J ].物理學報，2012，61（22）：26-33.

WEN Dezhi，ZHUO Renhong，Ding Dajie，et al . Gen ? eration? method? of random? number? sequence? of related variables? in? Monte? Carlo? simulation [ J ]. Acta? PhysicaSinica，2012，61（22）：26-33.

[18]楊正權，趙劍明，劉小生，等.超深厚覆蓋層上土石壩動力分析邊界處理方法研究[ J ].土木工程學報，2016，49（2）：138-143.

YANG Zhengquan，ZHAO Jianming，LIU Xiaosheng， et al . Study on boundary processing method for dynamic analysis of earth-rockfill dam? on super-deep overburdenlayer [ J ]. China? Civil? Engineering? Journal ，2016，49（2）：138-143.

[19]董景剛.土與結構接觸面力學特性研究[ D ].大連：大連理工大學，2011.

Dong Jinggang . Study on mechanical properties of inter? face between soil and structure[ D ]. Dalian：Dalian Uni? versity of Technology，2011.

[20]鄒德高，韓慧超，孔憲京，等.近斷層脈沖型地震動作用下面板堆石壩的動力響應[ J ].水利學報，2017，48（1）：78-85.

ZOU? Degao，HAN? Huichao，KONG? Xianjing，et? al . Seismic? response? of? a? concrete-faced? rockfill? dam? to near-fault pulse-like ground motions[ J ]. Journal of Hy? draulic Engineering，2017，48（1）：78-85.

[21]沈珠江，徐剛.堆石料的動力變形特性[ J ].水利水運科學研究，1996（2）：143-150.

SEHN? Zhujiang，XU? Gang . Deformation? behavior? of rock? materials? under? cyclic? loading [ J ]. Hydro-Science and Engineering，1996（2）：143-150.

[22]吳長彬，燕喬.堆石料的鄧肯 E-B 模型參數敏感性分析[ J ].水電能源科學，2010，28（8）：94-96.

WU Changbin，YAN Qiao . Sensitivity analysis of Dun? can? E-B? model? parameters? for? rockfill [ J ]. Water? Re ? sources and Power，2010，28（8）：94-96.

[23]李炎隆，李守義，丁占峰，等.基于正交試驗法的鄧肯-張 E-B 模型參數敏感性分析研究[ J ].水利學報，2013，44（7）：873-879.

LI? Yanlong，LI? Shouyi，DING? Zhanfeng，et? al . The sensitivity analysis of Duncan-Chang E-B model param ? eters based on the orthogonal test method[ J ]. Journal of Hydraulic Engineering，2013，44（7）：873-879.

[24]楊玉生，劉小生，趙劍明，等.鄧肯 E-B 模型參數敏感性分析[ J ].中國水利水電科學研究院學報，2013，11（2）：81-86.

YANG? Yusheng ，LIU? Xiaosheng，ZHAO? Jianming， et al . Parameter sensitivity analysis of Duncan E-B mod ? el[ J ]. Journal of China Institute of Water Resources and Hydropower Research，2013，11（2）：81-86.

[25]羅博華.考慮覆蓋層材料空間變異性的土石壩動力響應分析及預測[ D ].西安：西安理工大學，2021.

LUO Bohua . Dynamic analysis and prediction of dynam ? ic? response? of? earth-rock ?dam? considering? spatial? vari? ability? of overburden material[ D ]. Xi’an：Xi’an Uni? versity of Technology，2021.

[26]蔣水華，李典慶，周創兵，等.考慮自相關函數影響的邊坡可靠度分析[ J ].巖土工程學報，2014，36（3）：508-518.

JIANG Shuihua，LI Dianqing，ZHOU Chuangbing，et al . Slope reliability analysis considering effect of autocor? relation? functions [ J ]. Chinese? Journal? of? Geotechnical Engineering，2014，36（3）：508-518.

[27]楊鴿，Griffiths D V，朱晟.考慮堆石料空間變異性的土石壩壩坡地震穩定性隨機有限元分析[ J ].地震工程學報，2019，41（4）：939-948.

YANG Ge，Griffiths D V ， ZHU Sheng . Seismic slope stability analysis of earth-rockfill dams considering spa? tial variability of rockfill materials via random finite ele? ment? method [ J ]. China? Earthquake? Engineering? Jour? nal，2019，41（4）：939-948.

[28] Chen? H ，Liu? D . Stochastic? finite? element? analysis? ofrockfill dam considering spatial variability of dam materi?al? porosity [ J ]. Engineering? Computations ，2019，36（9）：2929-2959.

[29]靳聰聰，遲世春，聶章博.基于地震變形易損性的高土石壩抗震安全分析[ J ].巖土工程學報，2020，42（2）：334-343.

JIN? Congcong，CHI? Shichun，NIE? Zhangbo . Seismic safety analysis of high earth-rockfill dams based on seis? mic deformational fragility[ J ]. Chinese Journal of Geo ? technical Engineering，2020，42（2）：334-343.

[30]龐銳，孔憲京，鄒德高，等.基于 MSA 法的高心墻堆石壩地震沉降易損性分析[ J ].水利學報，2017，48（7）：866-873.

PANG Rui，KONG Xianjing，ZOU Degao，et al . Seis? mic? subsidence? fragility? analysis? of high? CRFDs based on MSA[ J ]. Journal of Hydraulic Engineering ，2017，48（7）：866-873.

Research on seismic response of asphalt concrete core dam -overburden considering the spatial variability of material parameters

WANG Zong-kai，SONG Zhi-qiang，LIU Yun-he，WANG Fei

（State Key Laboratory of Eco-hydraulics in Northwest Arid Region of China，Xi ′an University of Technology，Xi ′an 710048，China）

Abstract： The spatial variability of overburden and dam material parameters significantly affects the seismic response of asphalt concrete core dam-overburden system . This paper proposes a space random field simulation technology based on number theory se? lection，and the random point sets distribution optimization is realized by using number theory selection method . The spatial correla?tions of material parameters and the spatial variability of material parameters are considered using normal or lognormal distribution and Gaussian autocorrelation relationship，respectively . Random parameter library is generated by covariance decomposition in Py? thon，and secondary script development is carried out for Abaqus finite element software . Based on the Monte Carlo method，the random? field simulation? and "non-invasive" random? finite? element calculation? considering the spatial difference? and? correlation? of dam-overburden material are realized . Taking an actual project as an example，the sensitive parameters in the static Duncan?Chang E-B constitutive model and the dynamic equivalent linear viscoelastic constitutive model are regarded as random parameters . The statistical law and probability distribution tests of the mean value，variation coefficient and 95% confidence interval limit value of the horizontal peak acceleration of the asphalt concrete core dam and the vertical permanent deformation of the dam are analyzed . The influence of ground motion intensity on discrete degree of random response and transcendence probability relative to determi? nate value is also analyzed . The result shows that the point selection method through number theory can significantly optimize the random point set distribution and improve computational efficiency . The randomness of material parameters will cause the seismic response of the dam to increase with a high probability，and the spatial difference of dam body and overburden materials has a great? er impact on the peak horizontal acceleration of the top of the dam and core wall than on the permanent deformation . The statistical results of the seismic response of the dam do not necessarily conform to the normal or lognormal distribution . Ignoring the spatial variability of material parameters will cause an underestimation of the 50% to 90% probability of the seismic response of the as? phalt concrete core dam-overburden system under different conditions and different indexes . The dispersion of the seismic response results of the overburden layer is greater than that of the dam body and core wall .

Key words ： asphalt concrete core dam；seismic response；overburden；spatial variability；stochastic finite element

作者簡介：王宗凱（1997―），男，碩士研究生。電話：15353099793；E-mail：2200420084@stu .xaut .edu .cn。

通訊作者：宋志強（1981―），男，教授，博士生導師。電話：15929975587；E-mail：zqsong@xaut .edu .cn。