耗能增效慣容系統的自適應權重粒子群優化

潘超 韓笑 張瑞甫 張雪 逯靜洲

摘要：耗能增效是慣容減震系統的典型特征。為充分發揮此特性并同時滿足減震性能需求，提出將慣容減震結構耗能增效程度最大化作為目標，并以性能需求作為約束條件進行減震參數尋優。基于隨機振動理論推導慣容減震單自由度結構在白噪聲激勵下的解析解；建立最大耗能增效設計所對應等效約束優化問題的數學表達式。鑒于表達式的復雜性，采用魯棒性好且便于實現的粒子群算法對問題進行求解。在粒子群算法中引入自適應懲罰權重考慮約束條件，并采用自適應調整的慣性權重提高求解效率。基于 Python 語言編制了自適應權重粒子群算法程序對慣容減震結構最大耗能增效設計問題進行求解。設計實例的求解過程體現了自適應權重粒子群算法對求解慣容減震結構優化設計問題的有效性，動力時程分析結果表明設計參數實現了預設的減震性能需求。

關鍵詞：慣容系統；耗能增效；性能需求；約束優化；粒子群算法；自適應權重

中圖分類號： TU318??? 文獻標志碼： A??? 文章編號：1004-4523（2022）05-1233-09

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.021

引言

地震是危及人類生命及財產安全的重大自然災害之一，工程結構的破壞是地震災害的主要表現形式。在結構中增設減震裝置是降低地震響應、提高結構安全性的有效手段[1?2]。慣容系統是一種新型減震裝置[3?4]，其兩端點慣性、阻尼耗能增效的特性為結構減震控制提供了高效的解決方案。日本東北大學Ikago團隊[5]率先展開慣容系統的減震研究，首次提出并研制了完整意義上的慣容系統，即調諧黏滯質量阻尼器（TVMD），繼而給出了 TVMD 單自由度結構基于定點理論的參數設計方法。李超等[6]針對參數優化過程中忽略固有阻尼的問題提出了一種基于遺傳算法的 TVMD 優化方法，以獲得更合理的設計參數，同時也表現出智能算法在優化設計過程中的合理性。Faraj 等[7?8]提出利用沖擊能量管理吸收沖擊并存儲在專用裝置中來調節慣容器慣性質量的方法。羅建南等[9]提出了通過網絡綜合分析來系統地辨識最優慣容型減振器構型的方法。閻武通等[10]基于 H2優化理論對設置慣容系統的多自由度結構進行了參數優化方法。上述研究以最優控制為目標，忽略了與工程設計實際需求的聯系。 Pan 等[11?12]認為慣容減震結構應以結構性能需求為直接設計目標，并基于隨機振動理論提出兼顧控制效果與成本的慣容減震結構優化設計原則與方法。隨后，Zhang 等[13]基于隨機振動響應解析解發現了慣容系統的耗能增效原理，使慣容減震機理得到明確的物理闡釋，并為慣容減震結構參數設計提供了更直觀的思路。

基于耗能增效原理的設計方法涉及繁瑣的隨機振動響應表達式，采用常規數值優化算法時需要推導更繁瑣的梯度表達式，且需要較準確的初始解，這給慣容減震結構的參數優化造成了一定的困難。鑒于此，本文采用魯棒性好、原理簡單且便于編程實現的粒子群算法對其進行慣容系統的最大耗能增效優化設計。本文以混聯Ⅱ型慣容系統（TVMD）為研究對象[14]，首先基于慣容減震結構在白噪聲激勵下的隨機振動響應解析解，給出了慣容減震結構最大耗能增效優化設計的數學描述，采用 Python 語言編制相應自適應權重粒子群算法的計算機程序，進行非線性約束優化問題的求解，最后通過設計實例分析驗證了本文所提方法和所得參數的有效性。

1 慣容系統理論基礎

1.1 單自由度慣容系統運動方程

單自由度結構在地震激勵下的運動方程為：

式中? m，c，k 分別為單自由度結構的質量、阻尼和剛度；u，u?，分別為結構質點的位移、速度和加速度；ag 為地面運動加速度。

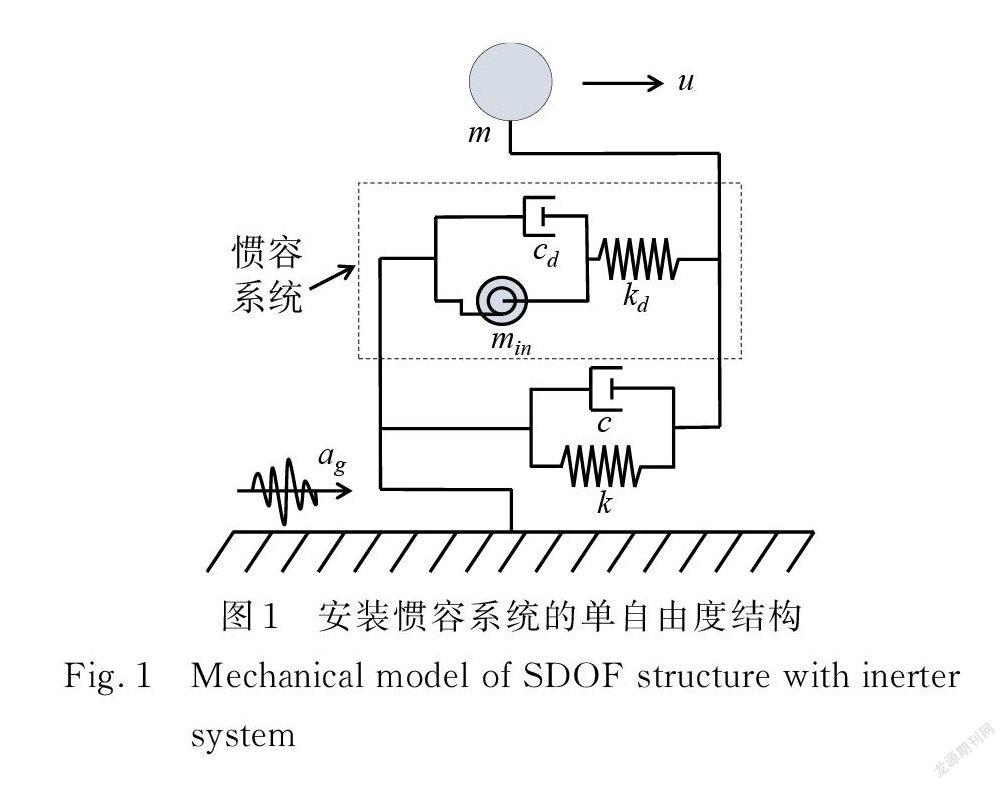
根據圖1建立設置慣容系統的單自由度結構的運動方程為：

式中? min，kd，cd 為慣容系統中的慣容系數、彈簧剛度、阻尼器的黏滯阻尼系數，uin為慣容元件兩端相對位移。

將式（2）中的等式左右兩邊同時除以質量 m可得

式中ω0，ζ分別為單自由度結構的自振圓頻率和固有阻尼比；μ，κ，ξ分別為慣容系統的慣質比、剛度比和名義阻尼比。各參數的具體定義如下：

1.2 隨機振動響應解析表達式

根據式（3）可推導出單自由度慣容減震結構位移響應的頻域傳遞函數：

根據隨機振動理論[15]，白噪聲（功率譜密度為 S0）激勵下，體系響應均方值為：

式中 H （ iω）為體系響應傳遞函數。

將式（5）代入式（7），可得慣容減震結構位移響應均方值的解析表達式為[12]：

基于隨機振動響應表達式可定義慣容減震結構的減震比γ為[11]：

式中σu（2），0為未安裝慣容系統的原單自由度結構的位移均方響應，表達式為：

將式（8），（12）代入式（11）即可得慣容減震結構隨機響應減震比的具體表達式為：

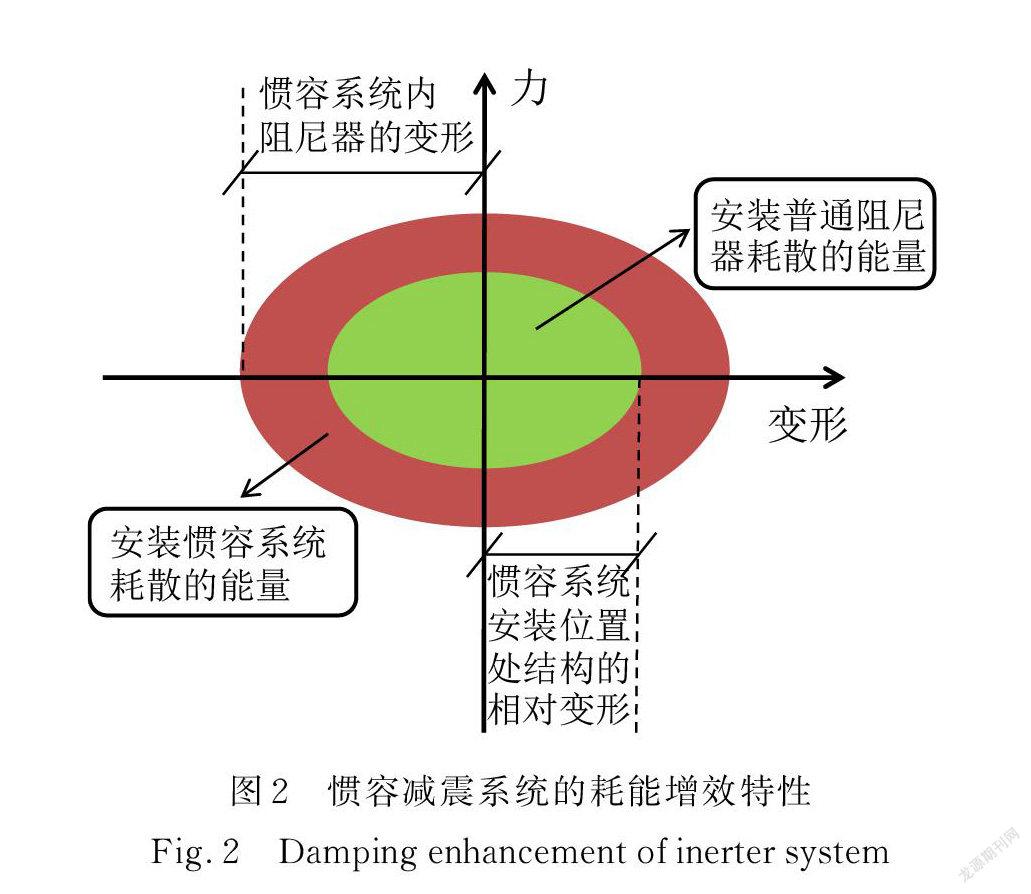
1.3 慣容系統的耗能增效特性

慣容系統耗能增效特性是指在動態荷載的激勵下，慣容系統內部自由度的變形可大于其安裝位置處主結構的相對變形[13]，從而高效地實現動力吸振與耗能減震。如圖2所示，結構變形一定的條件下，慣容系統的耗能增效特性比普通阻尼器耗散更多的輸入能量，進而降低動力響應。

為衡量耗能增效發揮的作用大小，文獻[13]定義了慣容系統的耗能變形放大率α為：

基于隨機振動響應解析表達式，求解白噪聲激勵下慣容系統耗能變形放大率α的具體表達式為[13]：

2 慣容系統的優化設計原則

為充分發揮慣容系統的耗能增效特性，本文以滿足性能需求為前提，以耗能變形放大率最大化為原則進行慣容系統參數的優化設計。慣容系統優化設計問題表示為約束優化問題，即：

式中 f為優化目標函數；慣容系統耗能變形放大率α按式（15）計算；減震比γ按式（13）計算；γ t 為目標減震比，設計時可按下式確定[12]：

求解式（18）所述約束優化問題時，若采用經典的數值方法，由于公式繁瑣、梯度計算不便，求解效果不夠理想。考慮到粒子群算法原理簡單且具有操作簡單、容易實現、全局搜索能力強等優點，本文選擇粒子群算法來對慣容減震結構進行參數尋優。

3 自適應權重粒子群算法

粒子群算法（Particle? Swarm? Optimization， PSO）是 Kennedy 和 Eberhart[16]提出的一種隨機優化算法，其模擬的是鳥群飛行覓食的行為，通過鳥群集體之間的協作使群體達到最優的目的，適用于求解復雜的非線性優化問題。

標準粒子群算法優化存在易出現早熟收斂、尋優精度低等問題。大量研究結果表明，慣性權重是粒子群算法中平衡全局搜索能力與局部搜索能力的重要參數，采用自適應慣性權重策略計算慣性權重可改善算法的性能[17?18]。考慮到慣容優化設計問題的目標函數和約束條件都是非線性函數，故本文選用可以自動調節慣性權重的改進粒子群算法進行求解。

粒子群算法求解優化問題時，單個粒子代表一個可行解，粒子適應度值根據優化目標函數計算，種群中所有個體按一定規則不斷移動以尋求最優解。粒子群中第i個粒子的移動規則為：

式中? t 為粒子移動時間步（t >0）；x? t ）為粒子i在t 時間步的位置向量，x i（b）est為粒子i在移動過程中的歷史最優位置向量，xbest為整個種群的歷史最優位置向量，v? t ）為粒子i在 t 時間步的速度向量；c1和 c2分別為粒子自身學習因子和社會學習因子；r1和 r2為0～1之間的隨機數；w （ t ）為自適應慣性權重系數，可按下式計算：

式中wmax和wmin分別為慣性權重的最大和最小值，一般取值分別為1.0，0.3；Ps （ t ）為移動到更優位置處粒子所占比例，可按下式計算：

式中? n 為種群規模，即種群中的粒子數量；f （ x t ））為粒子 i 在 t 時間步的適應度值。慣容系統耗能增效優化設計問題屬于約束優化問題，而粒子群算法本質上是一種無約束的搜索方法，因此本文采用懲罰函數法將慣容系統耗能增效優化設計問題轉化為無約束優化問題后，再運用粒子群算法進行求解。引入懲罰函數后，慣容系統耗能增效優化設計問題的表達式為：

式中? h 為懲罰權重。由于合理的懲罰權重因具體問題而異，其數值不易確定，為提升算法的穩定性與收斂性，本文采用自適應變化的懲罰權重，即：

當使用粒子群算法求解慣容系統優化設計問題時，粒子適應度值按式（25）中優化目標函數計算，粒子位置向量 x? t ）為三維向量：

式中μ t ），ξi（ t ），κ t ）分別為粒子i在 t 時間步時慣容系統的慣質比、名義阻尼比、剛度比。

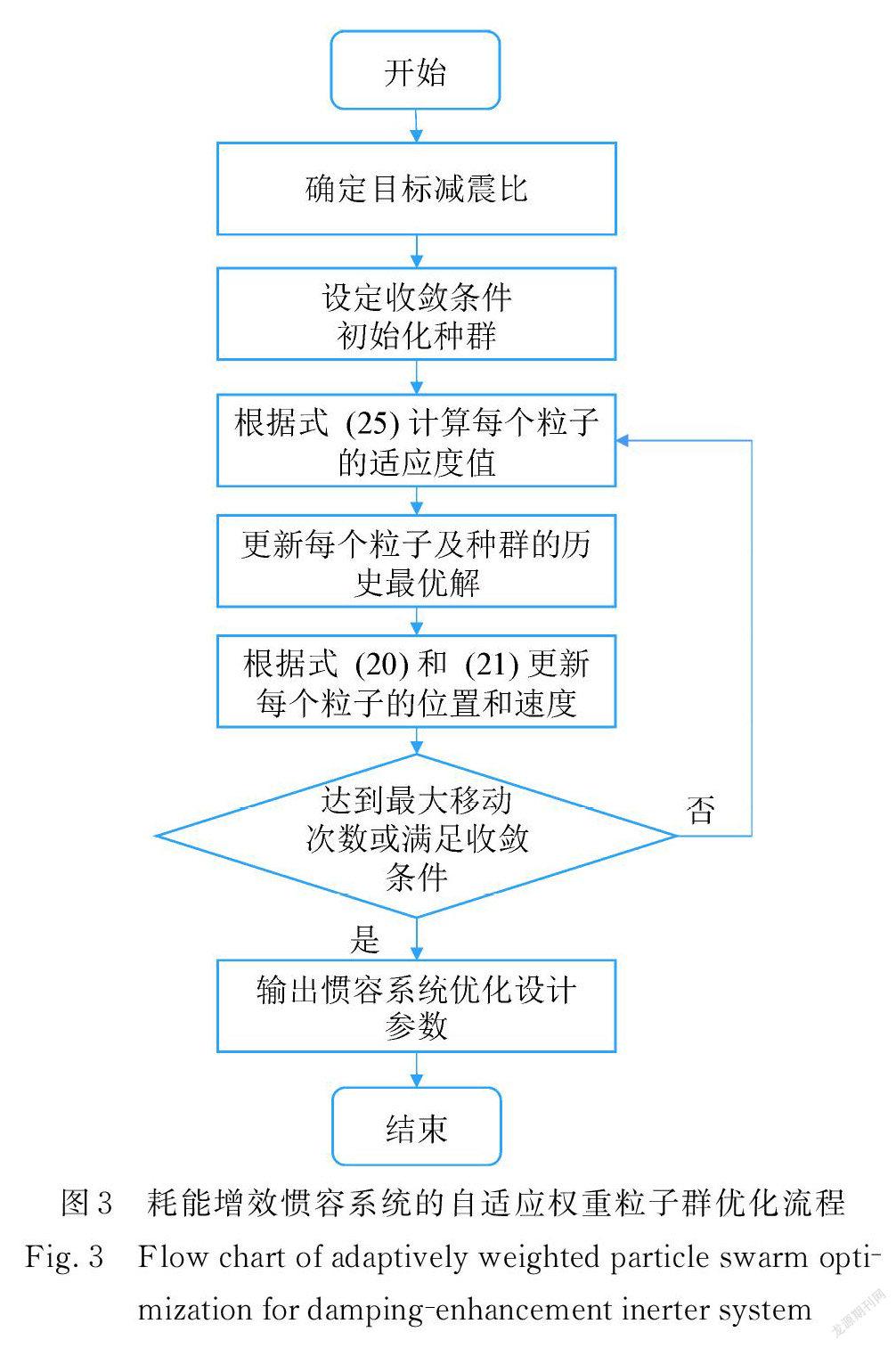
根據以上論述，可總結出采用自適應權重粒子群算法求解慣容系統耗能增效優化設計問題的流程（圖3）如下：

（1）根據性能需求確定結構的目標減震比γ t；

（2）設定粒子群最大移動次數或收斂條件，選定種群規模 n，初始化每個粒子的位置向量 x? t ）（個體歷史最優位置 x i（b）est亦按此初始化）和速度向量 v?; t ），根據式（25）計算每個粒子的適應度值，適應度最好的粒子所在位置即為種群的歷史最優位置向量xbest；

（3）根據式（25）計算每個粒子的適應度值， f （ x t ））與歷史最優位置相比適應度更好時，則相應更新每個粒子i的歷史最優位置向量x i（b）est、種群的歷史最優位置向量xbest；

（4）根據式（20），（21）更新各粒子的位置及速度；

（5）若粒子群達到最大移動次數或滿足收斂條件則停止移動，否則，重復步驟（3）～（5）；

（6）取最終的xbest為最優參數，得到慣容系統關鍵參數μ，ξ，κ。

據此流程，本文采用 Python 編程語言編制了面向對象的計算機程序 APSOIS（Adaptive ParticleSwarm Optimization of Inerter System）用以求解慣容系統的參數優化問題。

4 算例分析

4.1? 算例求解過程

某單自由度結構，其質量 m =1500 t，剛度 k =192 kN /mm，自振周期 T =0.56 s 。擬通過設置慣容系統進行減震控制。

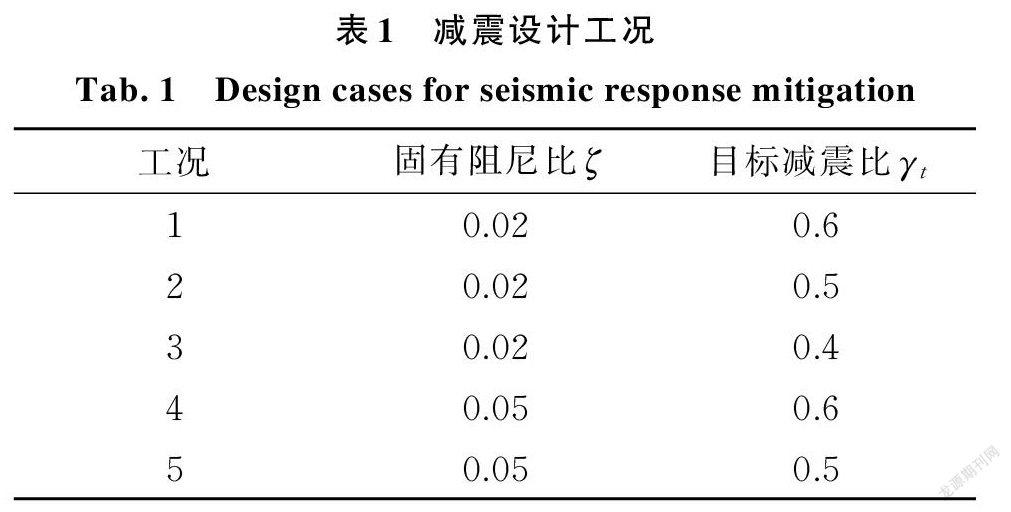
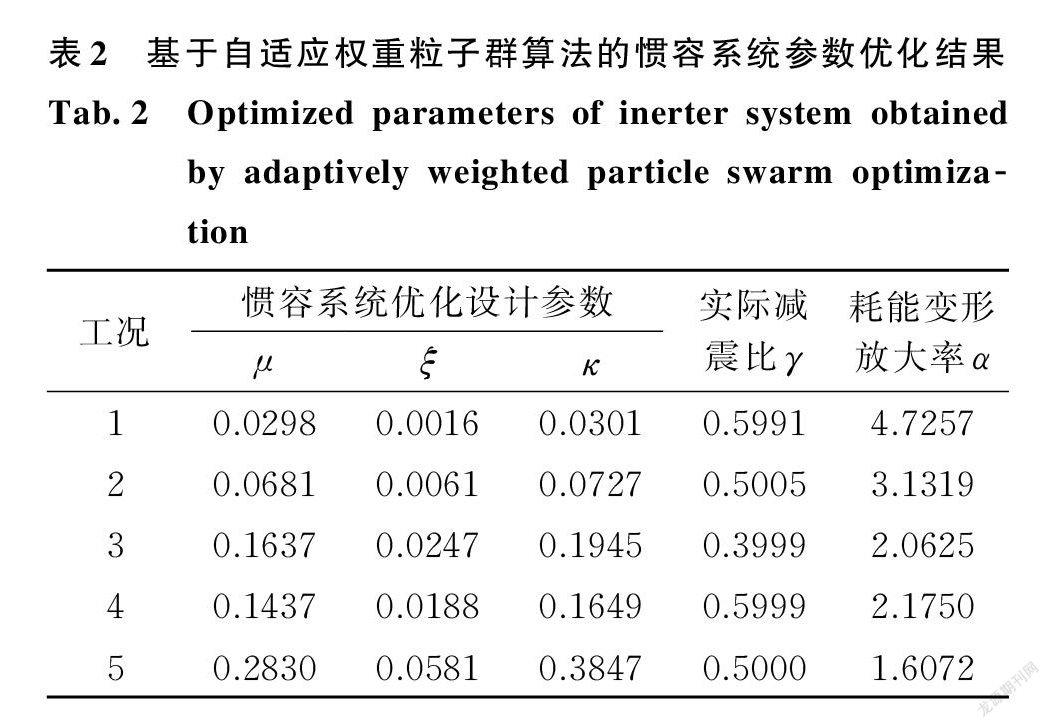
考慮固有阻尼比及目標減震比需求的不同，設置如表1所示5個設計工況。采用 APSOIS 程序求解慣容系統關鍵參數μ，ξ，κ的優化設計值如表2所示，同時給出各工況優化設計參數對應的實際減震比γ及耗能變形放大率α。為展示 APSOIS 程序求解慣容系統關鍵參數的過程，以工況4為例，AP ? SOIS 求解最優適應度值的迭代軌跡如圖4所示。

由圖4可知，迭代開始時種群中各粒子隨機分布，隨著粒子群移動次數的增加，粒子群不斷搜索到更好的適應度值，整個種群逐漸向最優解靠攏，最終大部分粒子都集中在最優解附近。

4.2? 算法性能

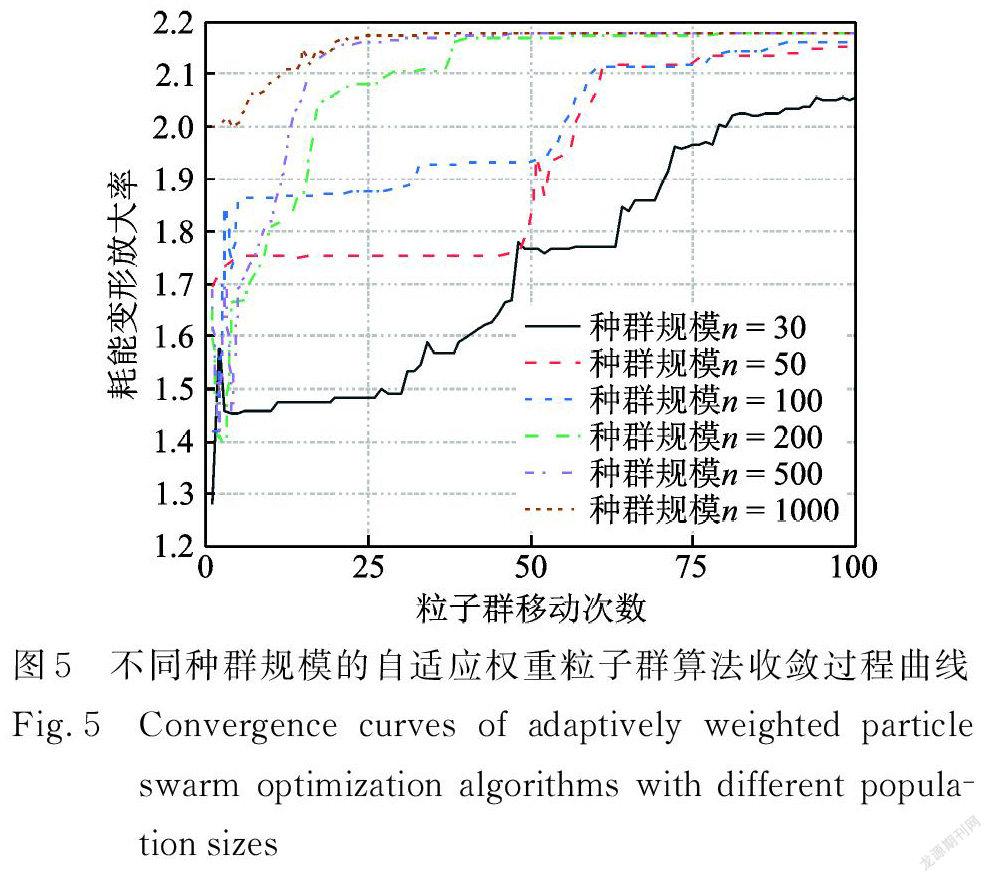
為了解自適應權重粒子群算法的性能，考察了種群規模、慣性權重策略、懲罰權重策略對自適應權重粒子群算法求解過程的影響。

算法收斂曲線。由圖可知，隨著種群規模增大，種群可獲得更好的初始最佳適應度值，且能以更少的移動次數收斂至最優解。由此，本文建議用自適應粒子群算法求解慣容系統優化設計問題時，可取種群規模200，最大移動次數100。

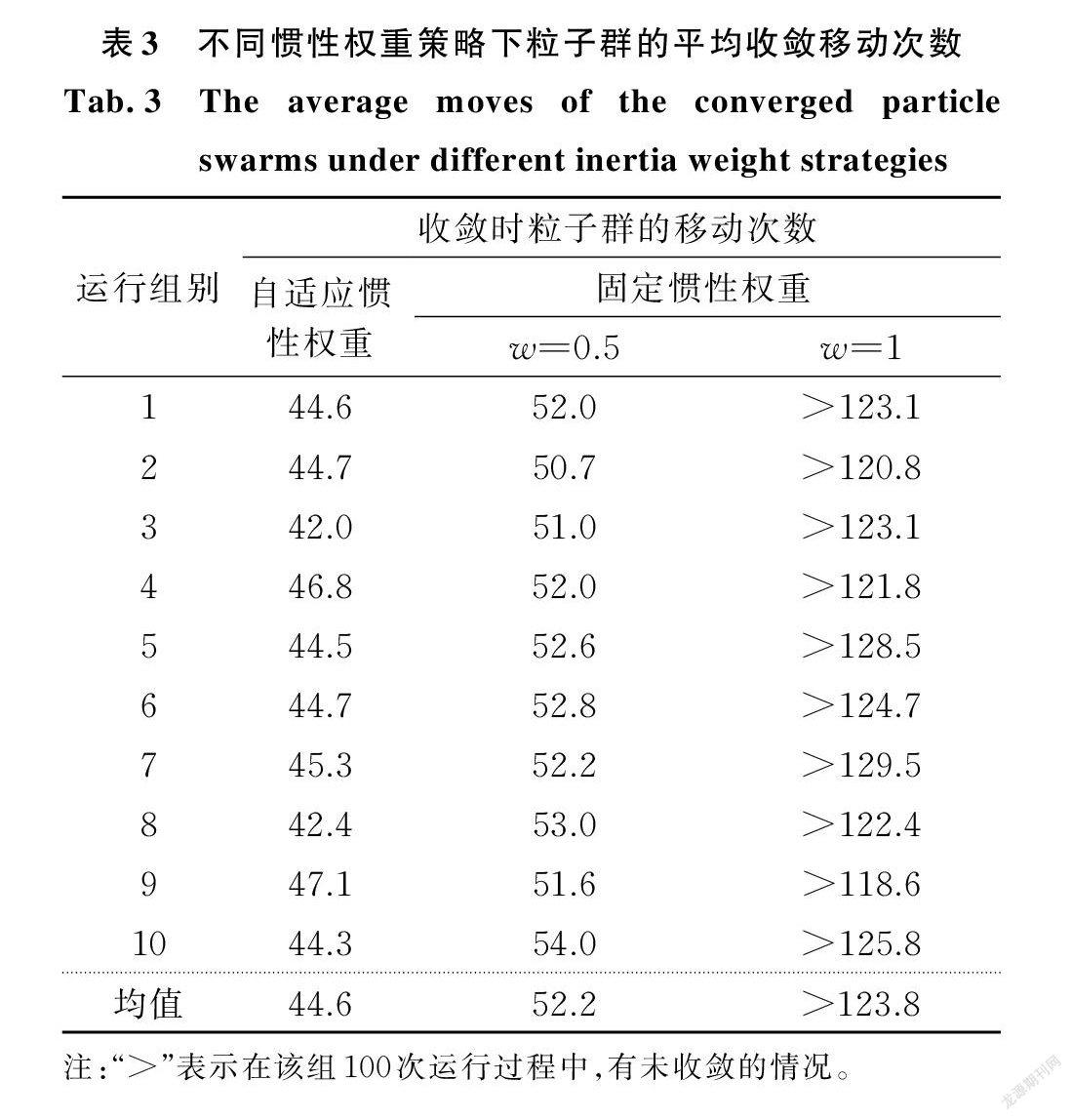
為驗證自適應慣性權重策略的優勢，以工況4為例，考慮不同的慣性權重策略，即自適應慣性權重、固定慣性權重（w=0.5，1），比較算法收斂時種群的移動次數。三種策略對應算法進行1000次求解（分為10組，每組100次），求解時設定粒子群種群規模為500，最大移動次數為200。收斂時每組所需平均移動次數如表3所示。

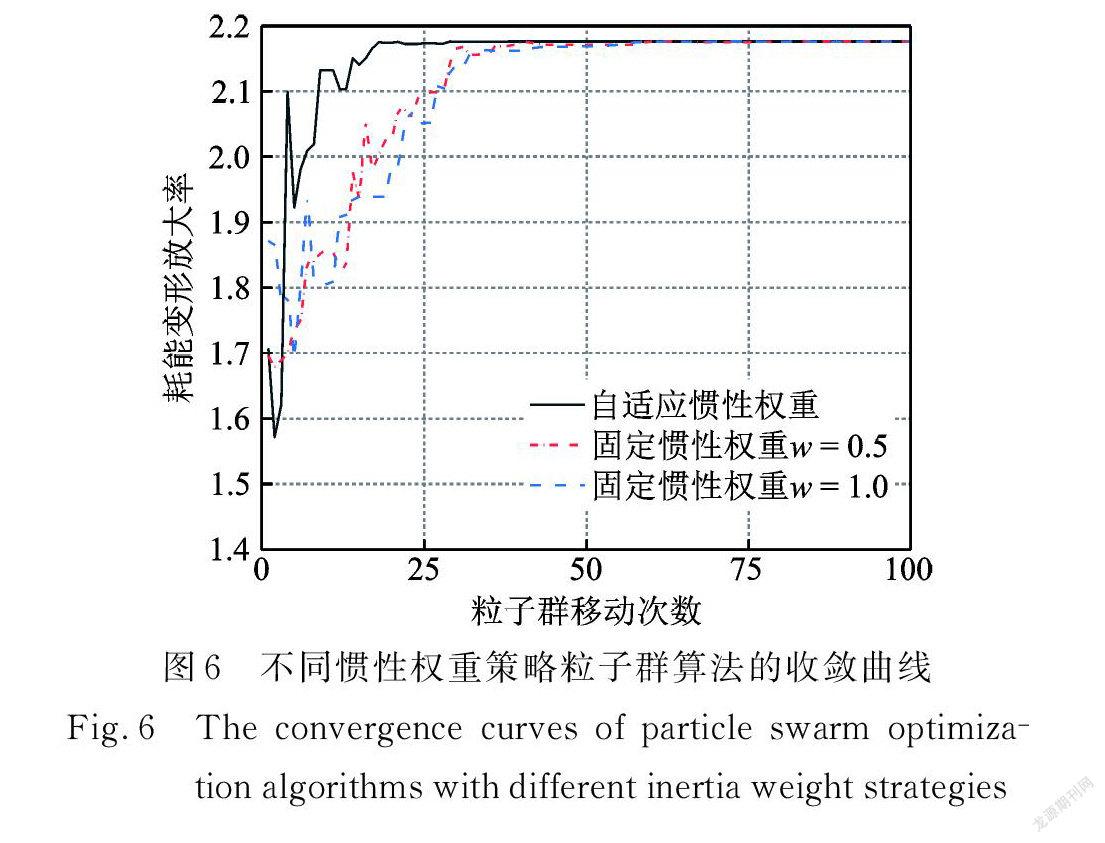
表3中每種策略對應的求解過程（成功收斂的情況）如圖6所示。判斷收斂成功的條件為：移動次數不超過最大移動次數的前提下，所得結果與種群規模1000、移動次數100次時結果之間相對誤差小于0.1%。由表3及圖6可知，自適應慣性權重策略下，算法的收斂移動次數小于固定慣性權重策略，表現出更強的求解能力。

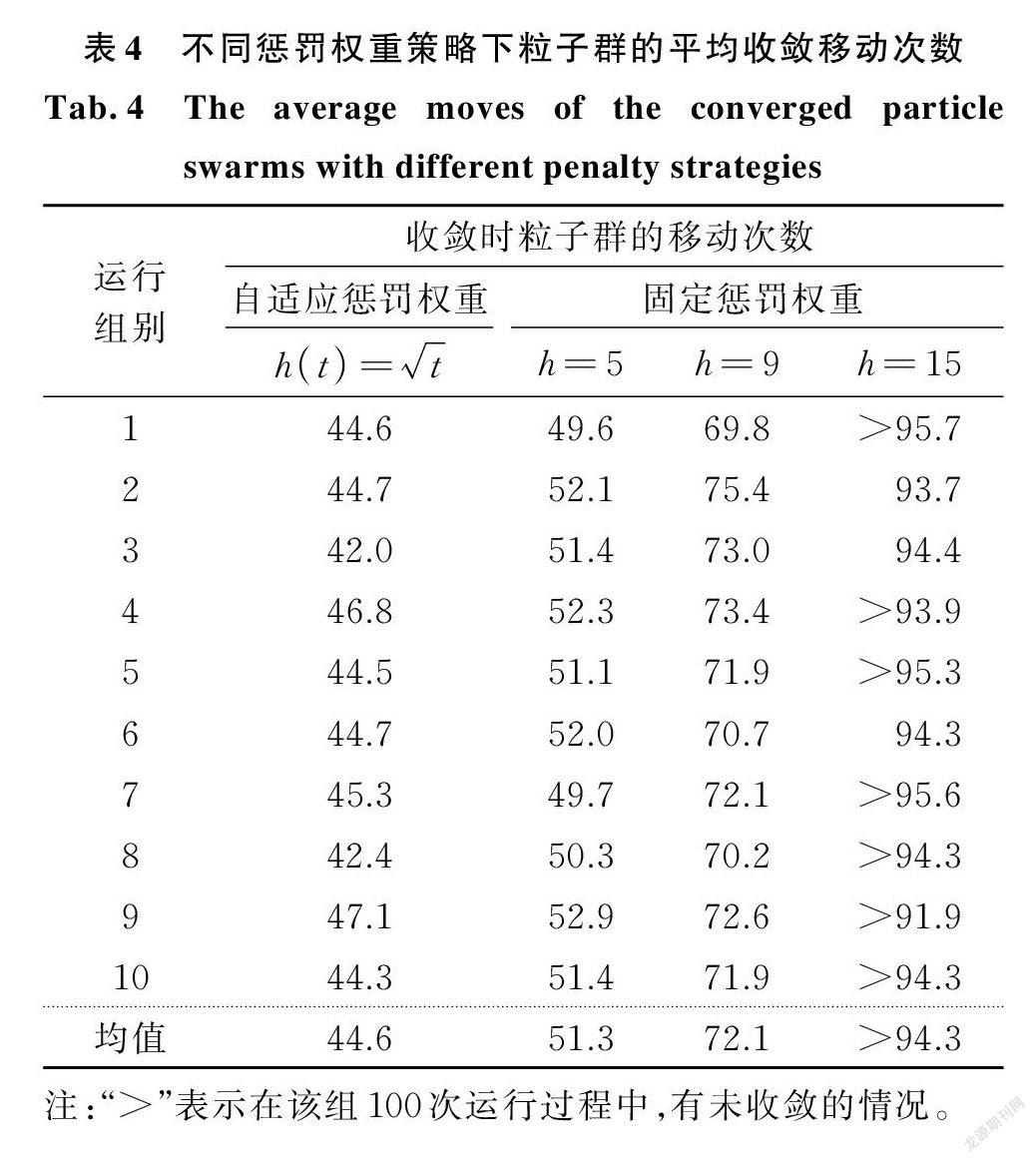
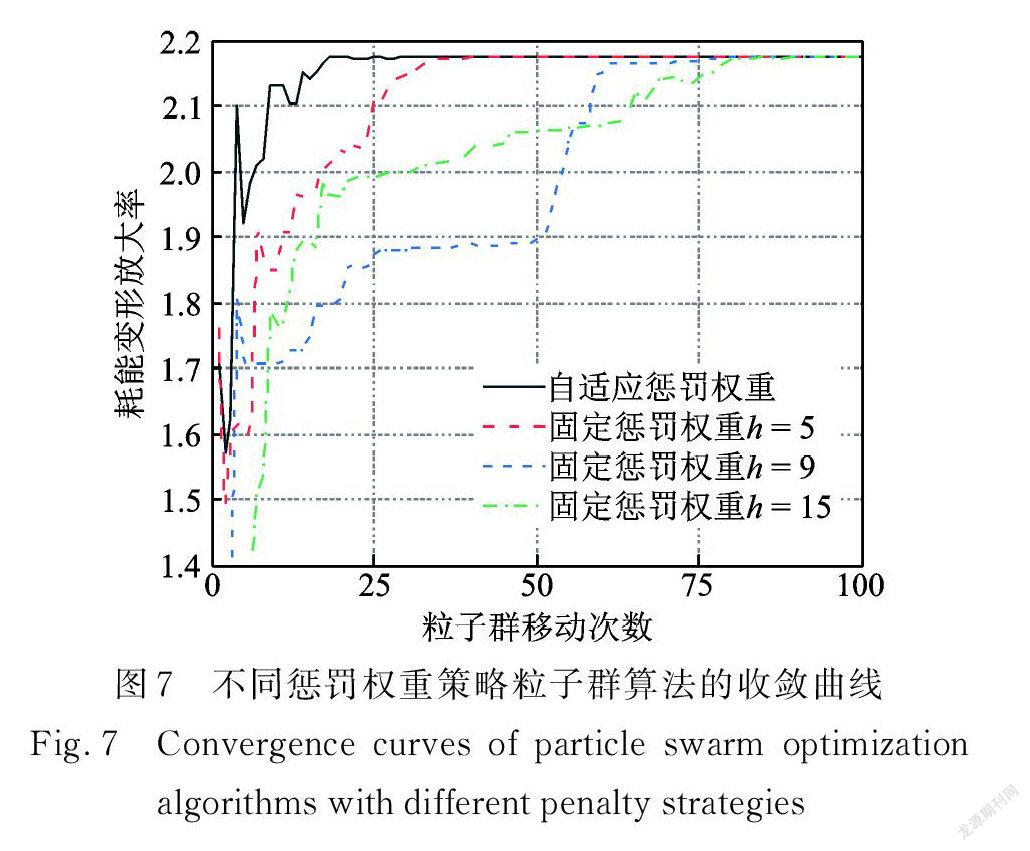
為驗證自適應懲罰權重策略的優勢，表4對比了自適應懲罰權重與固定懲罰權重為5，9，15時算法的收斂移動次數，相應收斂曲線如圖7所示。由表4及圖7可知，采用自適應懲罰權重策略的粒子群算法，其收斂移動次數小于固定懲罰權重策略的收斂移動次數。

4.3? 減震性能

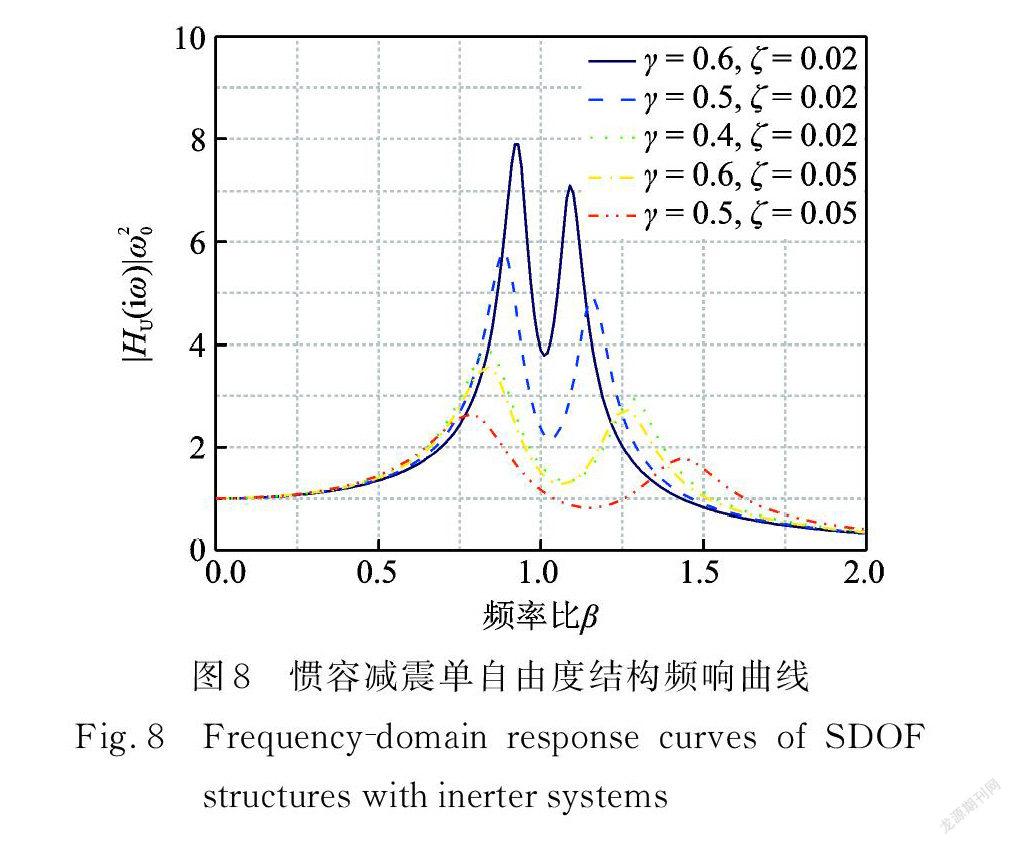
將表2自適應權重粒子群算法優化的慣容系統關鍵參數代入位移響應頻響函數解析表達式（5）可得其頻響曲線，如圖8所示。基于自適應權重粒子群算法所得參數可以有效調諧并控制單自由度結構的地震響應。

為驗證在有效控制地震響應的同時是否充分發揮慣容系統的耗能增效作用，將其與已有簡化設計方法進行對比。根據Ikago等[19]提出的單自由度慣容減震結構設計方法，在已知慣容系統的μ后，κ和ξ可以通過下式計算：

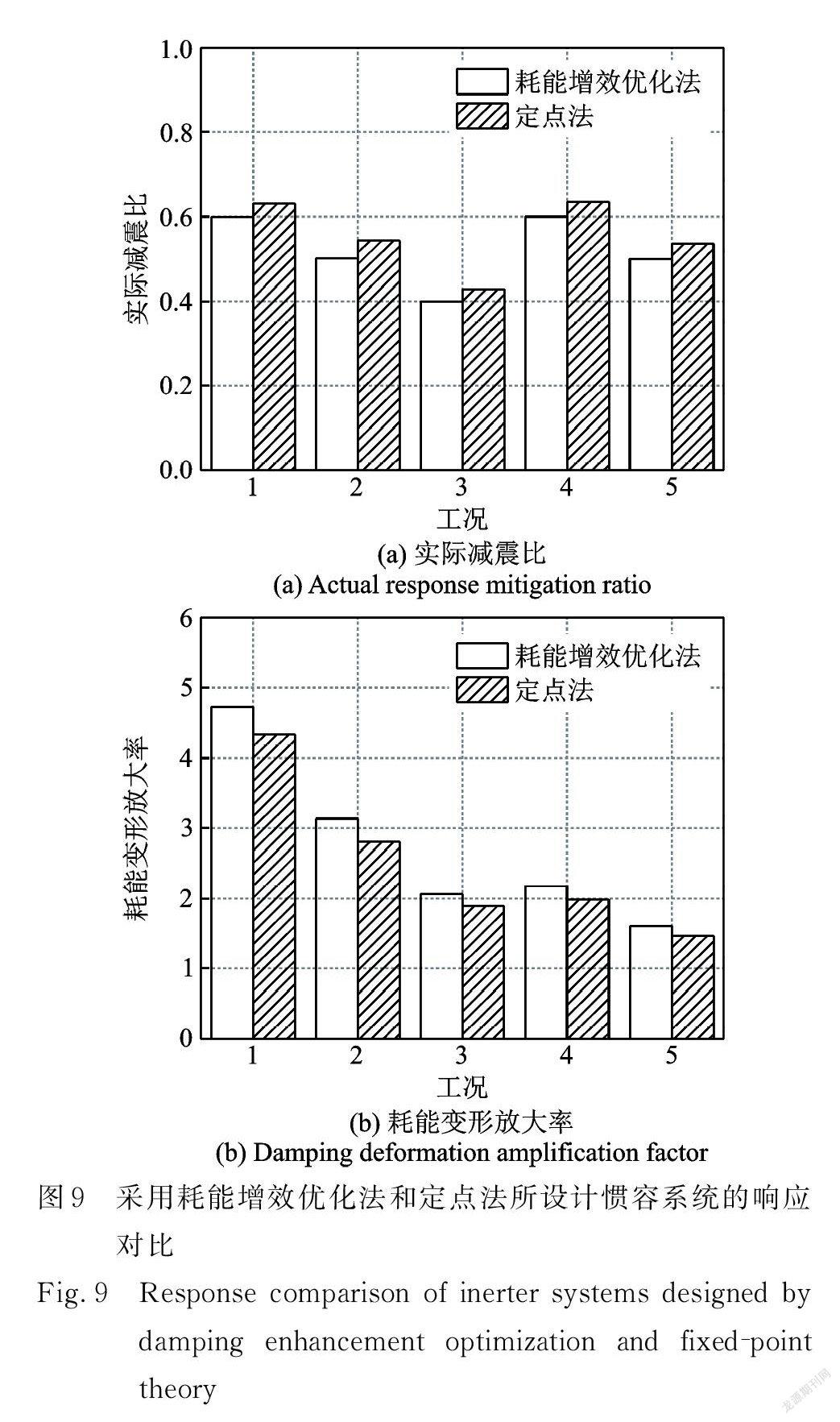
令式（29）中名義阻尼比ξ與表2中數值相等，可反算出對應的慣質比μ，進而根據式（28）計算出剛度比κ。這樣可以在名義阻尼比ξ相同的條件下對兩種方法的計算結果進行比較。使用Ikago方法得到的詳細結果如表5所示。根據表2和5的數據，可得本文方法與Ikago方法在耗能增效程度和減震效果角度的對比情況如圖9所示。對比可得，當二者名義阻尼比ξ一樣時，在相同的工況下，所編自適應權重粒子群算法所得優化參數計算出的減震比γ與目標減震比γt 更相近，更符合所需減震結構的性能水準，具體大小對比如圖9（ a ）所示。另外，如圖9（b）所示，自適應權重粒子群算法所求得耗能變形放大率α均大于定點法所得耗能變形放大率，即在名義阻尼比一定的條件下，自適應權重粒子群算法優化的慣容參數能更大程度發揮慣容系統的耗能增效作用。通過與定點法對比證明了自適應權重粒子群算法優化參數設計的慣容減震結構能夠充分發揮慣容系統的耗能增效作用。

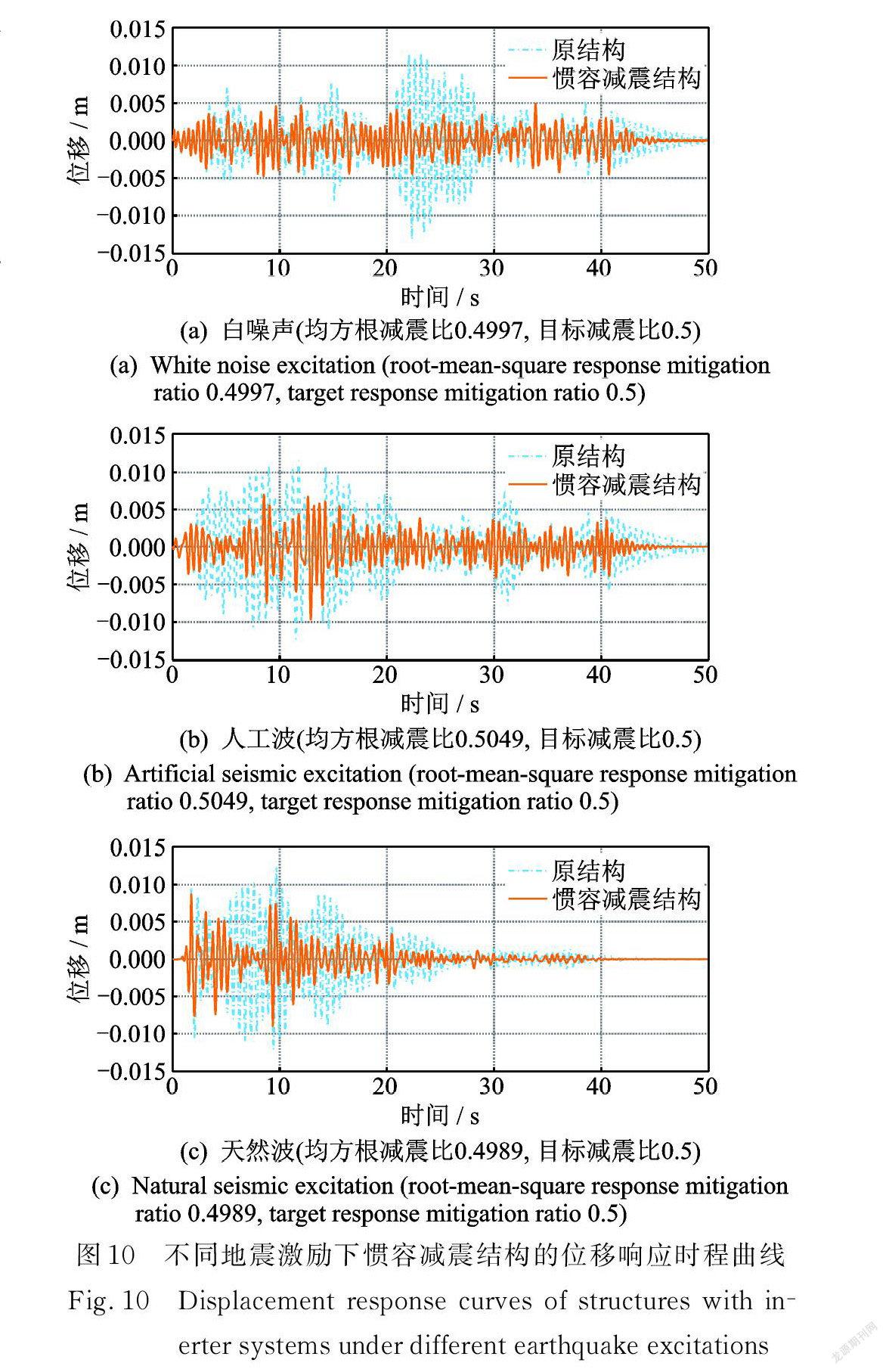
為直觀展示慣容系統的減震效果，取工況2的設計參數，將慣容減震結構與原結構進行動力時程分析，通過輸入具有不同頻譜特性的地震動[14]（白噪聲、人工地震波、天然波），計算其位移響應如圖10所示。圖 10顯示在不同頻譜地震動下慣容減震結構的位移響應均小于原結構的位移響應，且響應均方根減震比與所設定目標減震比均相近，證明了本文方法的有效性和設計參數的合理性。

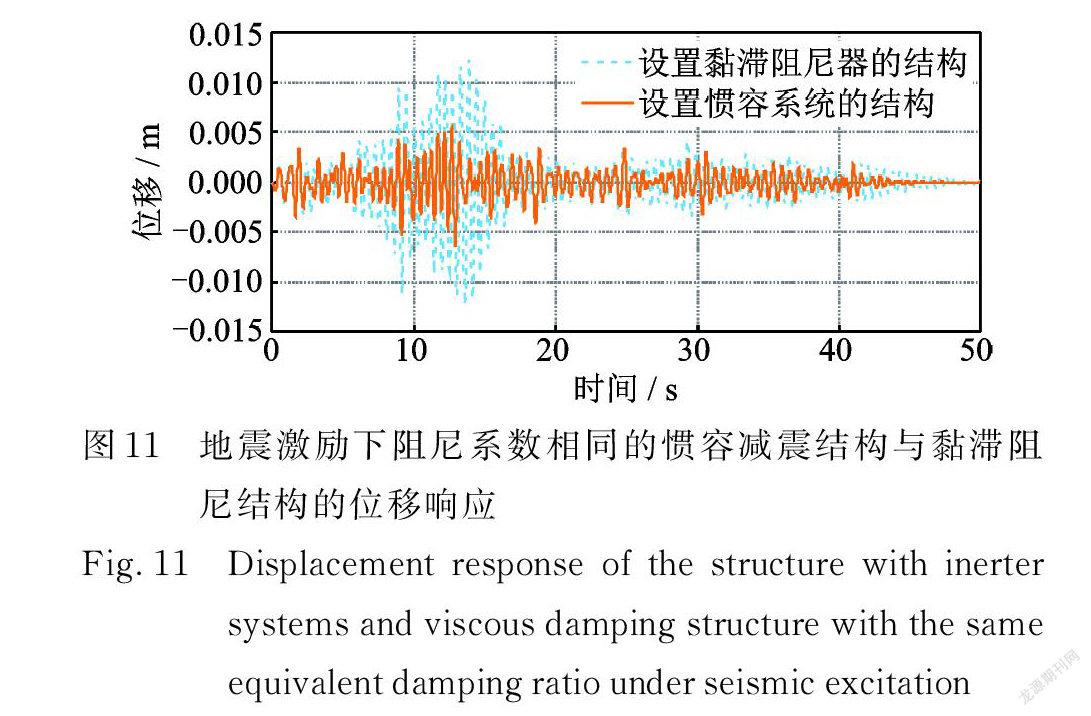
為體現慣容系統內阻尼器的減震效率，取工況2的設計參數，將慣容減震結構和單獨設置黏滯阻尼器的減震結構（二者的黏滯阻尼系數相等）進行地震響應對比，結果如圖11所示。由圖可知，慣容減震結構的響應明顯小于黏滯阻尼減震結構的響應，表現出更高的減震效率。

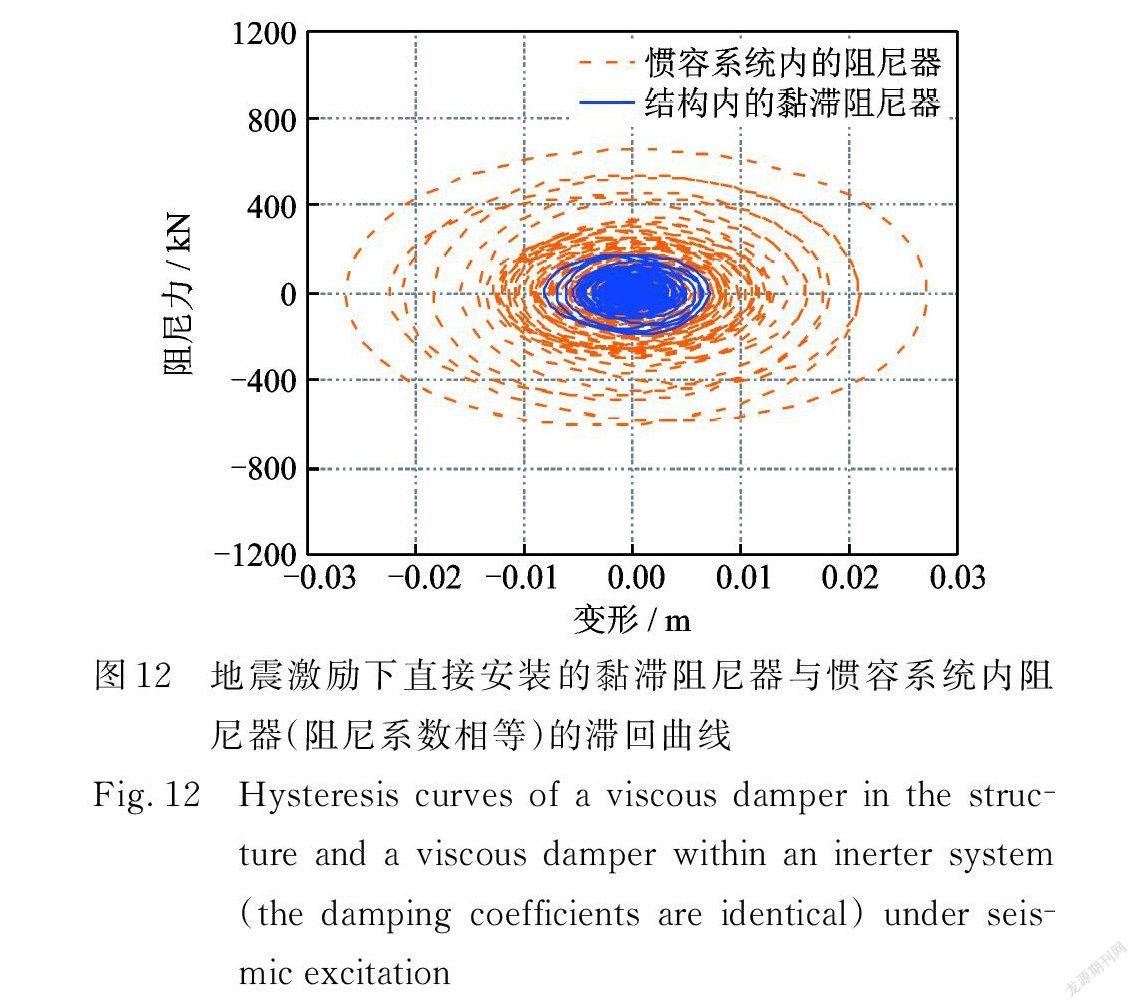
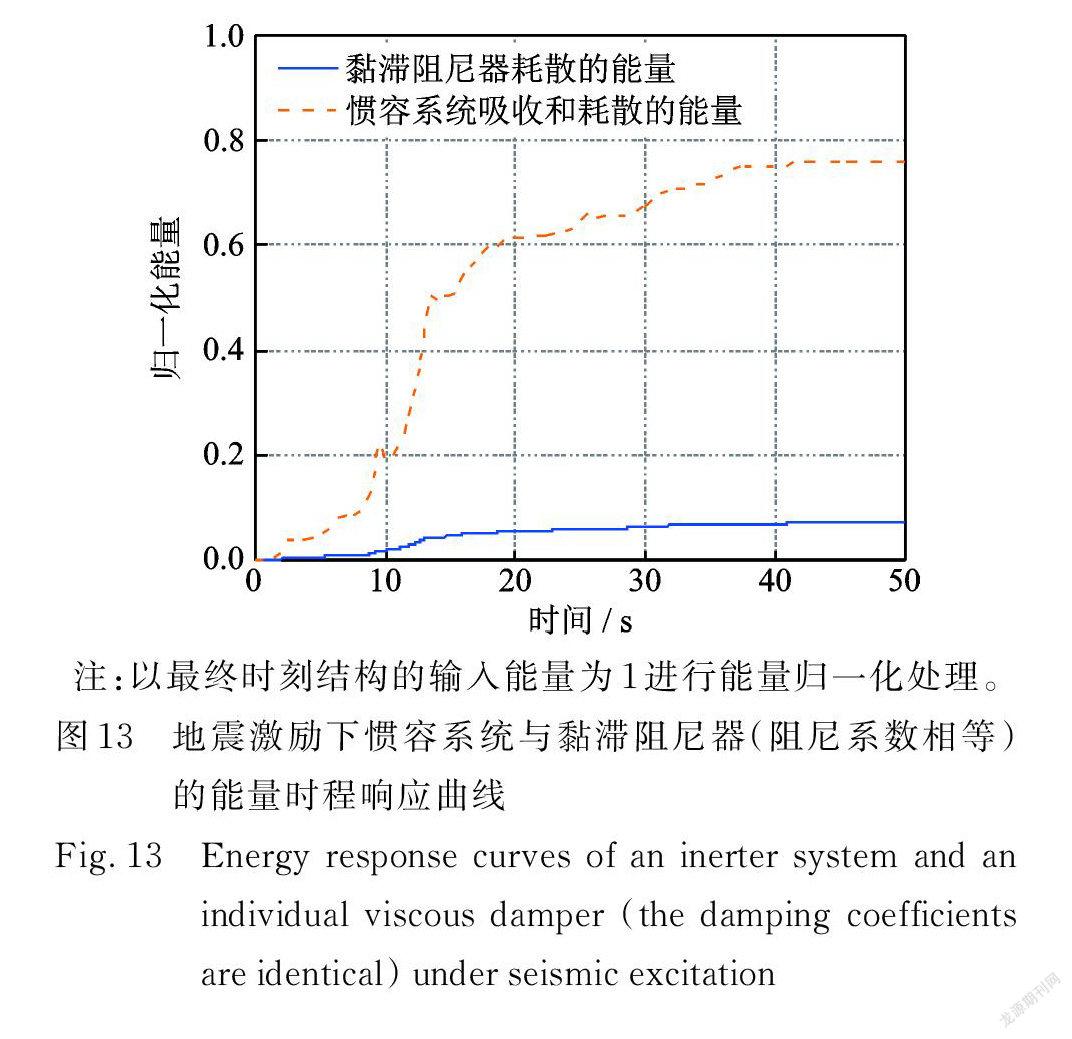
此外，本文還將慣容系統和黏滯阻尼器（二者黏滯阻尼系數相等）同時安裝在結構中，以比較兩者的耗能情況，結果如圖12所示。通過滯回曲線的對比可知慣容系統內阻尼器的變形、阻尼力明顯大于設置的黏滯阻尼器，其所耗散能量（滯回曲線所包裹的面積）也顯著增加。圖 13給出了相應的能量響應曲線，由圖可看出在整個地震激勵過程中，慣容系統吸收和耗散的能量都顯著大于黏滯阻尼器（約10倍）。

5 結論

本文采用自適應權重粒子群算法實現了對慣容系統的耗能增效優化設計。結論如下：

（1）慣容減震系統的最大耗能增效優化設計問題可描述為約束優化問題，約束條件可采用懲罰函數的方式予以考慮。

（2）采用自適應權重粒子群算法求解慣容系統優化問題，無需復雜的數學理論，便于理解及編程實現。

（3）與經典粒子群算法相比，考慮自適應慣性權重和自適應懲罰權重的粒子群算法在求解慣容系統優化問題時具有更好的收斂性能。

（4）雖然本文僅對設置慣容系統的單自由度結構進行了討論，但將本文方法框架中的響應求解過程和優化目標函數、約束條件等因素根據多自由度結構的特點進行調整后，即可用于多自由度慣容減震結構的優化，相關問題將在后續的研究中進一步探討。

參考文獻：

[1]? Saaed T E，Nikolakopoulos G，Jonasson J E，et al . Astate-of-the-art review? of structural control systems[ J ]. Journal of Vibration & Control，2013，21（5）：919-937.

[2]? Symans M D，Charney F A，Whittaker A S，et al . En ?ergy? dissipation? systems ?for? seismic? applications ：cur? rent? practice? and? recent? developments [ J ]. Journal? of Structural Engineering，2008，134（1）：3-21.

[3] 李壯壯，申永軍，楊紹普，等.基于慣容-彈簧-阻尼的結構減振研究[ J ].振動工程學報，2018，31（6）：157-163.

Li Zhuangzhuang，Shen Yongjun，Yang Shaopu，et al . Study? on? vibration? mitigation? based? on? inerter-spring- damping? structure [ J ]. Journal? of? Vibration? Engineer? ing，2018，31（6）：157-163.

[4] 張瑞甫，曹嫣如，潘超.慣容減震（振）系統及其研究進展[ J ].工程力學，2019，36（10）：8-27.

Zhang? Ruifu， Cao? Yanru，Pan? Chao . Inerter? system and? state-of-the-art[ J ]. Engineering Mechanics ，2019，36（10）：8-27.

[5]? Ikago K，Saito K，Inoue N . Seismic control of single-degree-of-freedom? structure? using? tuned? viscous? mass damper[ J ]. Earthquake? Engineering & Structural? Dy? namics，2012，41（3）：453-474.

[6] 李超，張瑞甫，趙志鵬，等.調諧黏滯質量阻尼器基于遺傳算法的參數優化研究[ J ].結構工程師，2016，32（4）：124-131.

Li Chao，Zhang Ruifu，Zhao Zhipeng，et al . Optimum study? of tuned? viscous mass dampers based? on? genetic algorithm [ J ]. Structural? Engineers ， 2016， 32（4）：124-131.

[7]? Faraj R，Holnicki-Szulc J，Knap L，et al . Adaptive in?ertial? shock-absorber [ J ]. Smart? Materials &Struc? tures，2016，25（3）：035031.

[8]? Faraj R，Jankowski U，Graczykowski C，et al . Can theinerter be? a? successful shock-absorber？The? case? of a ball-screw inerter with a variable thread lead[ J ]. Journalof the Franklin Institute，2019，356：7855-7872.

[9] 羅建南，景興建，姜政.采用網絡綜合分析的最優慣容型減振器辨識方法研究[ J ].振動工程學報，2020，33（6）：1208-1215.

Luo Jiannan，Jing Xingjian，Jiang Zheng . Identification approach of optimum inerter-based absorbers using net? work? synthesis [ J ]. Journal? of? Vibration? Engineering，2020，33（6）：1208-1215.

[10]閻武通，韓冰，文永奎.新型調諧黏滯質量阻尼器對斜拉橋的減震控制分析[ J ].土木工程學報，2016（S1）：66-71.

Yan? Wutong，Han? Bing ，Wen? Yongkui . Seismic? con ? trol analysis? of cable-stayed bridge based? on tuned? vis?cous [ J ]. China? Civil? Engineering? Journal ，2016（S1）：66-71.

[11] Pan C，Zhang R，Luo H，et al . Demand-based optimaldesign? of? oscillator? with? parallel-layout? viscous? inerter damper[ J ]. Structural Control and Health Monitoring，2018，25（1）：e2051.

[12] Pan? C，Zhang? R . Design? of structure with? inertersys?tem? based? on? stochastic? response? mitigation? ratio [ J ]. Structural Control & Health Monitoring，2018，25（6）：e2169.1-e2169.21.

[13] Zhang R，Zhao Z，Pan C，et al . Damping enhancementprinciple? ofinerter? system [ J ]. Structural? Control? and Health Monitoring，2020，27（5）：e2523.

[14]潘超，張瑞甫，王超，等.單自由度混聯Ⅱ型慣容減震體系的隨機地震響應與參數設計[ J ].工程力學，2019，36（1）：132-140+148.

Pan Chao，Zhang Ruifu，Wang Chao，et al . Stochastic seismic response and design of structural system with se? ries-parallel-II inertersystem[ J ]. Engineering Mechan? ics，2019，36（1）：132-140+148.

[15] Crandall S H M W D . Random Vibration in MechanicalSystems [M].?? New? York： Academic? Press，1963：127-139.

[16] Kennedy? J ， Eberhart ?R . Particle? swarm? optimization[C]. ICNN95-International Conference on Neural Net? works . IEEE，1995：1942-1948.

[17]鄧愛萍，王會芳.動態改變慣性權重的自適應粒子群算法[ J ].計算機工程與設計，2010（13）：3062-3065.?? Deng Aiping，Wang Huifang . Adaptive particle swarm optimizationalgorithm? with? dynamically? changing? iner?tia weight[ J ]. Computer Engineering and Design，2010（13）：3062-3065.

[18]周俊，陳璟華，劉國祥，等.粒子群優化算法中慣性權重綜述[ J ].廣東電力，2013（7）：6-12.

Zhou Jun，Chen Jinghua，Liu Guoxiang，et al . Summa ? ry on inertia weightin particle swarm? optimization algo? rithm[ J ]. Guangdong Electric Power，2013（7）：6-12.

[19] Ikago K，Saito K，Inoue N . Seismic control of single-degree-of-freedom? structure? using? tuned? viscous? mass damper[ J ]. Earthquake? Engineering & Structural? Dy? namics，2012，41（3）：453-474.

Adaptively weighted particle swarm optimization for damping enhanced inerter system

PAN Chao1，HAN Xiao1，ZHANG Rui-fu2，3，ZHANG Xue1，LU Jing-zhou1

（1.College of Civil Engineering，Yantai University，Yantai 264005，China；2.State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China；3.Department of Disaster Mitigation for Structures，Tongji University，Shanghai 200092，China）

Abstract： Damping enhancement is the typical characteristic of the inerter system for seismic response mitigation . To give full play to this characteristic and meet the demand of seismic performance at the same time，it is proposed to maximize the degree of damp? ing enhancement of the inerter system with the performance demand as the constraint condition during the decision of key parame ? ters . The closed-form solution of a single-degree-of-freedom structure with an inerter system under the excitation of white noise is derived based on the theory of random vibration . The mathematical expression of the equivalent constrained optimization problem for damping enhancement maximization is established . Given the complexity of the expression，the particle swarm algorithm，a ro ? bust and simple meta-heuristics method for numerical optimization，is used to solve the problem . The adaptively changed penalty weight is introduced into the particle swarm algorithm to consider the constraints，and the adaptively adjusted inertia weight is used to improve the efficiency for the search of the optimal solution . A computer program of the adaptively weighted particle swarm algo? rithm is developed to solve the design problem of the inerter system for damping enhancement maximization . The design examples reflect the effectiveness of the adaptively weighted particle swarm? algorithm? in solving the optimization problem? of the structure with inerter system . And the dynamic time-history? analyses show that the structural damping performance demands are realized with the designed parameters .

Key words ： inerter? system；damping? enhancement；performance? demand；constrained? optimization；particle? swarm? optimization； adaptive weight

作者簡介：潘超（1985—），男，副教授。電話：15953572531；E-mail：panchao@ytu .edu .cn。

通訊作者：張瑞甫（1980—），男，副教授。電話：13585903611；E-mail：zhangruifu@tongji .edu .cn。