基于距離優(yōu)勢關(guān)系的高維多目標(biāo)進(jìn)化算法

顧清華，徐青松，李學(xué)現(xiàn)

1.西安建筑科技大學(xué) 管理學(xué)院，西安710001

2.西安建筑科技大學(xué) 資源工程學(xué)院，西安710001

3.西安市智慧工業(yè)感知計(jì)算與決策重點(diǎn)實(shí)驗(yàn)室，西安710001

在實(shí)際生活中，如無人機(jī)任務(wù)規(guī)劃、雷達(dá)的波形設(shè)計(jì)等問題往往是高維多目標(biāo)優(yōu)化問題[1]。多目標(biāo)優(yōu)化進(jìn)化算法是解決這些問題的重要手段，但是現(xiàn)有的多目標(biāo)優(yōu)化算法在處理高維多目標(biāo)問題上會(huì)面臨維數(shù)詛咒難題。傳統(tǒng)的Pareto 支配關(guān)系很難有效區(qū)分非支配層級，導(dǎo)致種群的大多數(shù)個(gè)體都處于非支配層級。為了解決這一問題，許多學(xué)者從增大選擇壓力出發(fā)提出了新的方法來克服這一問題，根據(jù)增大選擇壓力方式的不同，這些方法大致分為三類：

第一種策略是發(fā)展新的優(yōu)勢關(guān)系，主要思想是增加兩個(gè)候選解在多目標(biāo)優(yōu)化問題上的可比性。Sato等提出了控制解的支配區(qū)域[2]的方法，使用三角函數(shù)通過設(shè)定參數(shù)來改變目標(biāo)函數(shù)的適應(yīng)度值，進(jìn)而使解的優(yōu)勢區(qū)域發(fā)生改變。雖然控制優(yōu)勢區(qū)域能增強(qiáng)算法的選擇壓力，但是參數(shù)難以確定，不恰當(dāng)?shù)膮?shù)設(shè)定會(huì)降低算法的多樣性。定義模糊優(yōu)勢關(guān)系，在L-支配[3]中通過比較優(yōu)劣解的個(gè)數(shù)以及目標(biāo)函數(shù)的范數(shù)來比較個(gè)體間的優(yōu)勢關(guān)系。在(1-k)-支配[4]中通過預(yù)設(shè)的參數(shù)k比較劣解集及相等解的個(gè)數(shù)來確定個(gè)體的優(yōu)勢關(guān)系。在模糊支配[5]通過高斯公式轉(zhuǎn)換兩個(gè)個(gè)體的表現(xiàn)值，表現(xiàn)值相乘得出的值相比較來定義優(yōu)勢關(guān)系。這種方式的好處在于能有效化解目標(biāo)維度的增加帶來的Pareto優(yōu)勢互相抵消，但是這種方式并不能有效保證算法的收斂性。

第二種策略是將原有的Pareto 優(yōu)勢與特定的選擇方式結(jié)合。通過Pareto 優(yōu)勢來進(jìn)行初次比較淘汰劣解后再進(jìn)行二次選擇。例如KnEA[6]在二元錦標(biāo)賽中結(jié)合支配關(guān)系引入拐點(diǎn)準(zhǔn)則和加權(quán)距離，利用非支配解拐點(diǎn)的偏向來提高算法的收斂性。在VaEA[7]中通過最大角優(yōu)先原則與消除差解原則選擇收斂性與分布性更好的解參與進(jìn)化，但是這使得算法不能很好解決規(guī)則Pareto前沿面問題。

第三種策略是將傳統(tǒng)的Pareto 優(yōu)勢與基于分解的思想相結(jié)合，既保留了Pareto 支配的支配層級，又結(jié)合了基于分解的適應(yīng)度值和獨(dú)立子空間等特性。在MOEADD[8]中保留基于分解的子空間特征，通過引入Pareto支配關(guān)系增強(qiáng)更新過程中算法的收斂性，并且設(shè)計(jì)種群局部密度維護(hù)算法多樣性。在RPDNSGA-Ⅱ[9]中提出了一種基于分解的支配關(guān)系，并且引入?yún)⒖键c(diǎn)。結(jié)合Pareto 支配并按照參考點(diǎn)關(guān)聯(lián)候選解的數(shù)量，以及計(jì)算候選解到理想點(diǎn)的距離來判斷解的優(yōu)劣。

雖然上述三種策略能一定程度上增強(qiáng)算法的性能，但是這些方法大多需要預(yù)先設(shè)定合適的參數(shù)，而且較難維持算法在高維多目標(biāo)問題上的多樣性，使得大多數(shù)的非支配解集聚集在前沿面上的一小部分區(qū)域。基于存在的問題，為了增強(qiáng)算法在高維目標(biāo)空間中的多樣性，本文提出一種新的支配關(guān)系。首先，在非支配排序階段不僅考慮了收斂性，同時(shí)進(jìn)行了多樣性的維護(hù)，而且所提出的距離優(yōu)勢關(guān)系不需要預(yù)先定義參數(shù)。其次，結(jié)合所提出的距離優(yōu)勢關(guān)系對VaEA 算法進(jìn)行了改進(jìn)，不僅提升了VaEA 算法在高維多目標(biāo)問題上的性能，而且提升了VaEA算法解決規(guī)則Pareto前沿面問題的能力。最后，通過一系列測試問題驗(yàn)證所提出支配關(guān)系的適用性。

1 相關(guān)背景

1.1 高維多目標(biāo)優(yōu)化問題

高維多目標(biāo)優(yōu)化問題是指目標(biāo)維度超過4 的多目標(biāo)優(yōu)化問題，不失一般性，以最小化為例，高維多目標(biāo)的一般表現(xiàn)形式如下：

其中，m≥4，Ω是決策空間，x=(x1,x2…,xn)∈Ω是決策變量。

1.2 VaEA算法

VaEA算法是由Xiang等于2017年提出的一種基于向量角的多目標(biāo)進(jìn)化算法，VaEA算法的基本框架與大多數(shù)基于支配關(guān)系的算法類似，圖1給出了VaEA算法的流程圖。首先，在決策空間中隨機(jī)初始化生成N個(gè)個(gè)體的種群。然后，根據(jù)每個(gè)個(gè)體的適應(yīng)值選擇更優(yōu)的個(gè)體進(jìn)入交配池。在接下來的操作中，通過應(yīng)用交叉和變異操作來生成一組子代解Q，并合并父代與子代種群。最后，使用Pareto支配關(guān)系對合并后的種群進(jìn)行非支配排序，按照非支配層級由低到高加入外部檔案，并采用環(huán)境選擇操作使外部檔案的種群規(guī)模為N。VaEA算法的核心是設(shè)計(jì)了最大角優(yōu)先原則與消除差解原則，其中最大角優(yōu)先原則是指，優(yōu)先選擇臨界層中與外部檔案中個(gè)體關(guān)聯(lián)角度最大的個(gè)體加入外部檔案，這是為了增強(qiáng)種群的多樣性。另一方面，消除差解原則是為了維護(hù)種群的收斂性，將一些收斂性太差的個(gè)體剔除，選擇與這些差解多樣性相似，但是收斂性更好的個(gè)體加入外部檔案，直到外部檔案的種群規(guī)模為N。

圖1 VaEA算法流程圖Fig.1 Flow chart of VaEA algorithm

2 提出算法

2.1 整體框架

本文提出的VaEA-DDR 算法整體框架與VaEA算法一致，區(qū)別在于VaEA-DDR算法使用距離優(yōu)勢關(guān)系對種群進(jìn)行非支配排序。算法1給出了具體流程。

算法1VaEA-DDR算法流程

輸入：種群P，種群規(guī)模N，最大迭代次數(shù)Gmax。輸出：最終種群P。

2.2 距離優(yōu)勢關(guān)系

距離優(yōu)勢關(guān)系結(jié)合小生境技術(shù)[10]，不僅考慮到解的收斂性，同樣使解的多樣性得到了增強(qiáng)。具體來說，如果解X1距離支配解X2，即X1?DDRX2，則滿足下列條件：

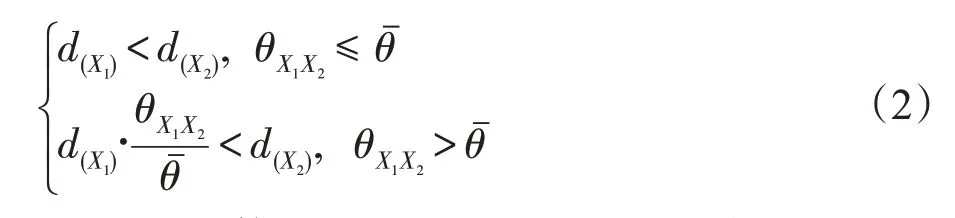
其中，d(X)是個(gè)體到理想點(diǎn)的歐氏距離，將這一距離作為適應(yīng)度值來選擇更優(yōu)的解。表示兩個(gè)候選解的目標(biāo)值之間的夾角，即：

算法2距離優(yōu)勢關(guān)系

輸入：種群P，種群規(guī)模N。

圖2 說明了距離優(yōu)勢關(guān)系在雙目標(biāo)空間的優(yōu)勢區(qū)域。從圖中可以看出，解X1的優(yōu)勢區(qū)域由兩部分組成，在設(shè)定的小生境內(nèi)根據(jù)候選解到理想點(diǎn)的距離可以得出區(qū)域1，根據(jù)式（2）中的第二個(gè)公式可以得出另一個(gè)優(yōu)勢區(qū)域2。解X1與解X2在同一小生境內(nèi)，比較兩個(gè)解到理想點(diǎn)的距離可以得出解X1?DDR解X2。解X1與解Y不在同一小生境內(nèi)，θX1Y＞，但是根據(jù)式（2）中第二個(gè)公式可以得出解X1?DDR解Y。從這里可以看出，某些目標(biāo)函數(shù)值較差的候選解可能會(huì)被認(rèn)為是非支配解，但是在這里并沒有試圖定義一種新的方式解決這個(gè)問題。一方面，這些較差的解還在預(yù)設(shè)的范圍內(nèi)，而且這些較差的非支配解數(shù)量較少，不會(huì)影響算法的收斂性；另一方面，如果將這些消除，這些差解將會(huì)極大增加距離優(yōu)勢關(guān)系的計(jì)算復(fù)雜度。

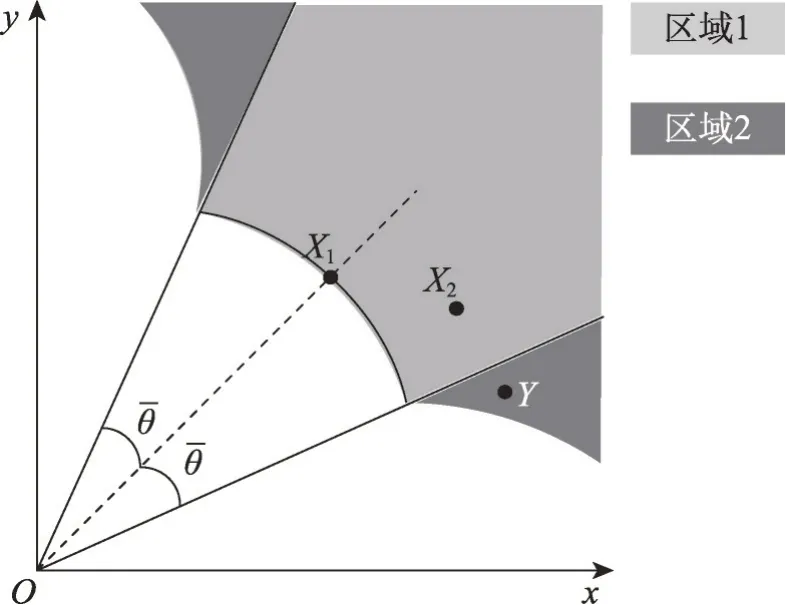
圖2 雙目標(biāo)空間中距離優(yōu)勢關(guān)系支配區(qū)域Fig.2 Dominated area of distance dominancerelationship in dual-objective space

圖3 雙目標(biāo)空間中不同種群分布示意圖Fig.3 Schematic diagram of distribution of different populations in dual-objective space

3 仿真實(shí)驗(yàn)與結(jié)果分析

3.1 測試問題與對比算法

為了驗(yàn)證VaEA-DDR算法性能，選取了DTLZ系列測試集進(jìn)行實(shí)驗(yàn)研究。表1 給出了測試問題及其特征。根據(jù)目前幾個(gè)主要的研究方向，選用近年最具有代表性的算法作為對比算法，包括NSGA-Ⅲ[11]、MOEADD[8]、MOMBI-Ⅱ[12]、RPD-NSGA-Ⅱ[9]、NSGA-Ⅱ-SDR[10]、VaEA[7]。

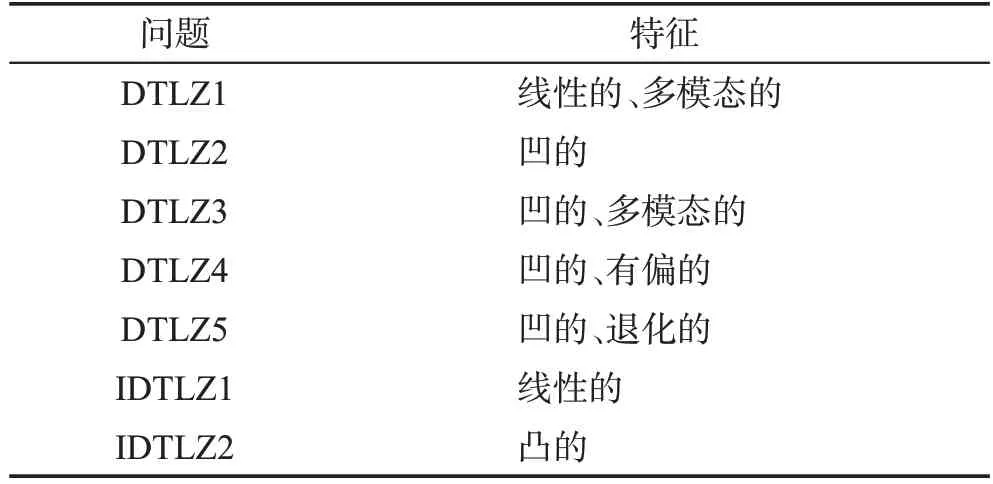
表1 測試問題及其特征Table 1 Test problems and their characteristics

3.2 性能評價(jià)指標(biāo)

文中采用的性能評價(jià)指標(biāo)主要有：反轉(zhuǎn)世代距離（inverted generational distance，IGD）[13]，該指標(biāo)是對收斂性和多樣性的綜合性評價(jià)指標(biāo)；廣義分布（Spread/Δ）[14]，該指標(biāo)主要評估算法多樣性；世代距離（generational distance，GD）[15]，該指標(biāo)主要評估算法收斂性。

設(shè)P為近似集，P*為沿真實(shí)帕累托前沿均勻分布的非支配點(diǎn)集，|P*|是P*中解的個(gè)數(shù)，|P|是P中解的個(gè)數(shù)，dist(z*,P)是z*與P中最近鄰域之間的歐幾里德距離。則三個(gè)性能評價(jià)指標(biāo)計(jì)算公式分別如下：

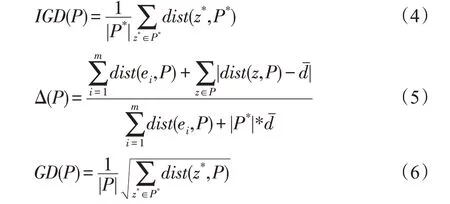
3.3 參數(shù)設(shè)置

實(shí)驗(yàn)過程中涉及的多目標(biāo)算法存在一些參數(shù)需要設(shè)定，具體如下：

（1）種群規(guī)模：表2 概述了不同數(shù)量目標(biāo)的種群規(guī)模N和權(quán)重向量的數(shù)量。

表2 權(quán)重向量的數(shù)量和種群規(guī)模Table 2 Number of weight vectors and population size

（2）鄰域規(guī)模：鄰域T的大小設(shè)置為0.1N。

（3）PBI中的懲罰因子：θ=5.0。

飛機(jī)在恐怖的黑暗中又堅(jiān)持飛行了近兩個(gè)鐘頭。一直沒有聲音的廣播突然傳出機(jī)長的緊急通知：“飛機(jī)遇到特大氣流，大家忍耐一下，正在聯(lián)系準(zhǔn)備迫降。”不知又過了多久，廣播中再次傳來了機(jī)長的通知，內(nèi)容大致是：飛機(jī)準(zhǔn)備迫降在阿拉斯加阿留申群島的薛米亞美國空軍基地。但是這個(gè)島太小，機(jī)場不具備降落大型民用客機(jī)的條件，跑道不夠長，沒有足夠的照明設(shè)施。加上眼下氣候惡劣，有大風(fēng)暴，能見度很低。我們飛機(jī)自身的受損情況不明，起落架不知道能不能打開。所以能否安全降落仍是未知數(shù)。請大家做好自救準(zhǔn)備！

（4）運(yùn)行次數(shù)及終止條件：每個(gè)算法在每個(gè)測試實(shí)例上獨(dú)立運(yùn)行30次，算法的終止條件是5、8、10、15目標(biāo)上算法運(yùn)行迭代次數(shù)分別為200、300、300、500次。

3.4 實(shí)驗(yàn)結(jié)果分析與討論

本節(jié)給出了VaEA-DDR算法與NSGA-Ⅲ、MOEADD、MOMBI-Ⅱ、RPD-NSGA-Ⅱ、NSGA-Ⅱ-SDR以及VaEA算法對比的實(shí)驗(yàn)結(jié)果。實(shí)驗(yàn)結(jié)果為在PlatEMO平臺[16]獨(dú)立運(yùn)行30 次結(jié)果的平均值與標(biāo)準(zhǔn)差。在PlatEMO 中，采用顯著性水平為0.05 的Wilcoxon 秩和檢驗(yàn)對結(jié)果進(jìn)行分析，“+”“-”“=”分別表示對比算法的結(jié)果比提出算法的結(jié)果好、差以及在統(tǒng)計(jì)學(xué)上相似。

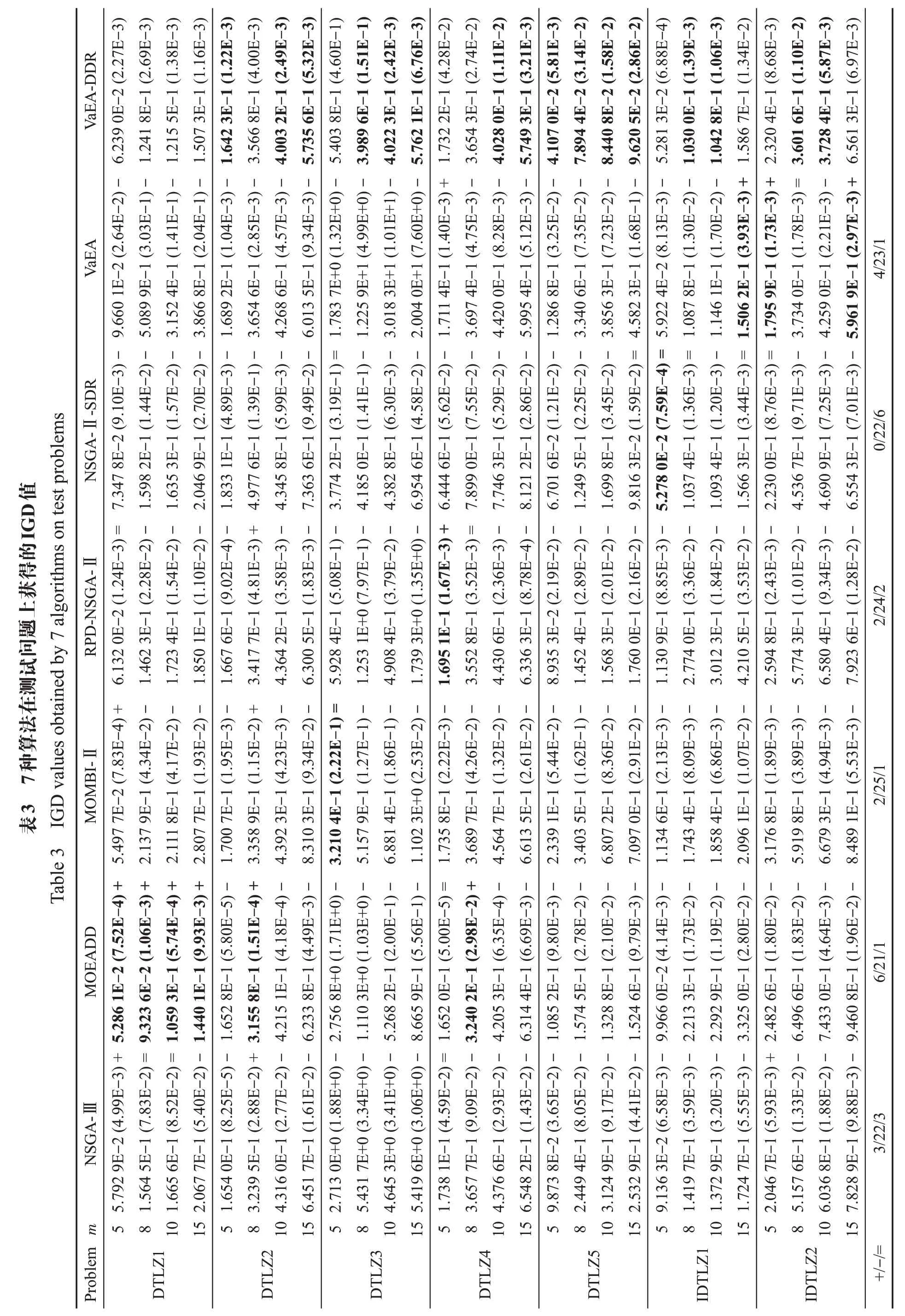
表3 給出了7 種算法在5、8、10、15 目標(biāo)DTLZ 與IDTLZ測試問題上獲得的IGD 平均值與標(biāo)準(zhǔn)差。從表中可以知道，VaEA-DDR算法所取得的最佳IGD值的個(gè)數(shù)為16 個(gè)。比NSGA-Ⅲ、MOEADD、MOMBI-Ⅱ、RPD-NSGA-Ⅱ、NSGA-Ⅱ-SDR以及VaEA取得更佳IGD值的個(gè)數(shù)分別為22、21、25、24、22、23。

VaEA-DDR 算法在DTLZ1 與IDTLZ1問題上表現(xiàn)不佳，在DTLZ1 測試問題上，MOEADD 算法為表現(xiàn)最佳的算法。在IDTLZ2 問題上，VaEA-DDR 與NSGA-Ⅱ-SDR 算法的IGD 值十分接近。這是因?yàn)镈TLZ1 與IDTLZ1 都是具有線性Pareto 最優(yōu)面的測試問題，但是在本文中定義的支配關(guān)系通過基于到理想點(diǎn)的距離來選擇適應(yīng)度更好的解，這種支配關(guān)系較難判斷線性平面上解的收斂程度。這可能會(huì)造成在解決具有線性平面的多目標(biāo)問題時(shí)，文中提出的算法較難具有很強(qiáng)的競爭力。

DTLZ2～5 是凹優(yōu)化問題，從實(shí)驗(yàn)結(jié)果可以知道VaEA算法表現(xiàn)最佳。為了更直觀了解IGD值的變化，圖4 給出了7 種算法在15 目標(biāo)上DTLZ2、DTLZ4、DTLZ5 以及IDTLZ2 的IGD 值變化曲線。從圖4（a）中可以看出VaEA-DDR算法最快降至最小值并穩(wěn)定在最小值，相比VaEA 算法在早期IGD 值收斂更快。MOMBI-Ⅱ算法IGD 值表現(xiàn)最差，NSGA-Ⅱ-SDR 算法的IGD 值出現(xiàn)了明顯的波動(dòng)，雖然在早期算法具有很好的收斂性，但是隨著迭代次數(shù)的增加IGD 值會(huì)迅速增加，這說明NSGA-Ⅱ-SDR算法在迭代過程的早期能很迅速接近最優(yōu)解，但是可能會(huì)出現(xiàn)遠(yuǎn)離最優(yōu)解集的情況。從圖4（b）中仍可以看出VaEA-DDR算法相對VaEA算法在前期IGD值下降更迅速。

DTLZ5 問題最后會(huì)收斂為一條退化曲線，在該問題上改進(jìn)的VaEA-DDR算法表現(xiàn)出絕對優(yōu)勢。對比VaEA 算法與VaEA-DDR 算法的實(shí)驗(yàn)結(jié)果可以看出，VaEA算法的性能僅相比MOMBI-Ⅱ算法有優(yōu)勢，這說明本文提出的距離優(yōu)勢關(guān)系對VaEA 算法的性能有較大提升。從圖4（c）可以看出大部分算法的IGD值出現(xiàn)了明顯的波動(dòng)，其中MOMBI-Ⅱ算法的IGD值一直處于上升趨勢，這說明算法形成的解正在遠(yuǎn)離Pareto前沿面。NSGA-Ⅲ、RPD-NSGA-Ⅱ、NSGA-Ⅱ-SDR 以及VaEA 算法出現(xiàn)了不同程度的波動(dòng)，但是VaEA-DDR 算法IGD 值一直處于下降趨勢，這說明VaEA-DDR能較好處理退化問題。

IDTLZ2 問題是一個(gè)凸優(yōu)化問題，從實(shí)驗(yàn)結(jié)果看VaEA-DDR 算法僅在8 目標(biāo)與10 目標(biāo)問題上具有最佳的IGD值。從圖4（d）可以看出在15目標(biāo)上VaEADDR 算法IGD 值下降與NSGA-Ⅱ-SDR 算法基本一致，最終僅比VaEA算法略差。這說明在凸優(yōu)化問題上，文中提出的距離優(yōu)勢關(guān)系對算法性能的提升較小。

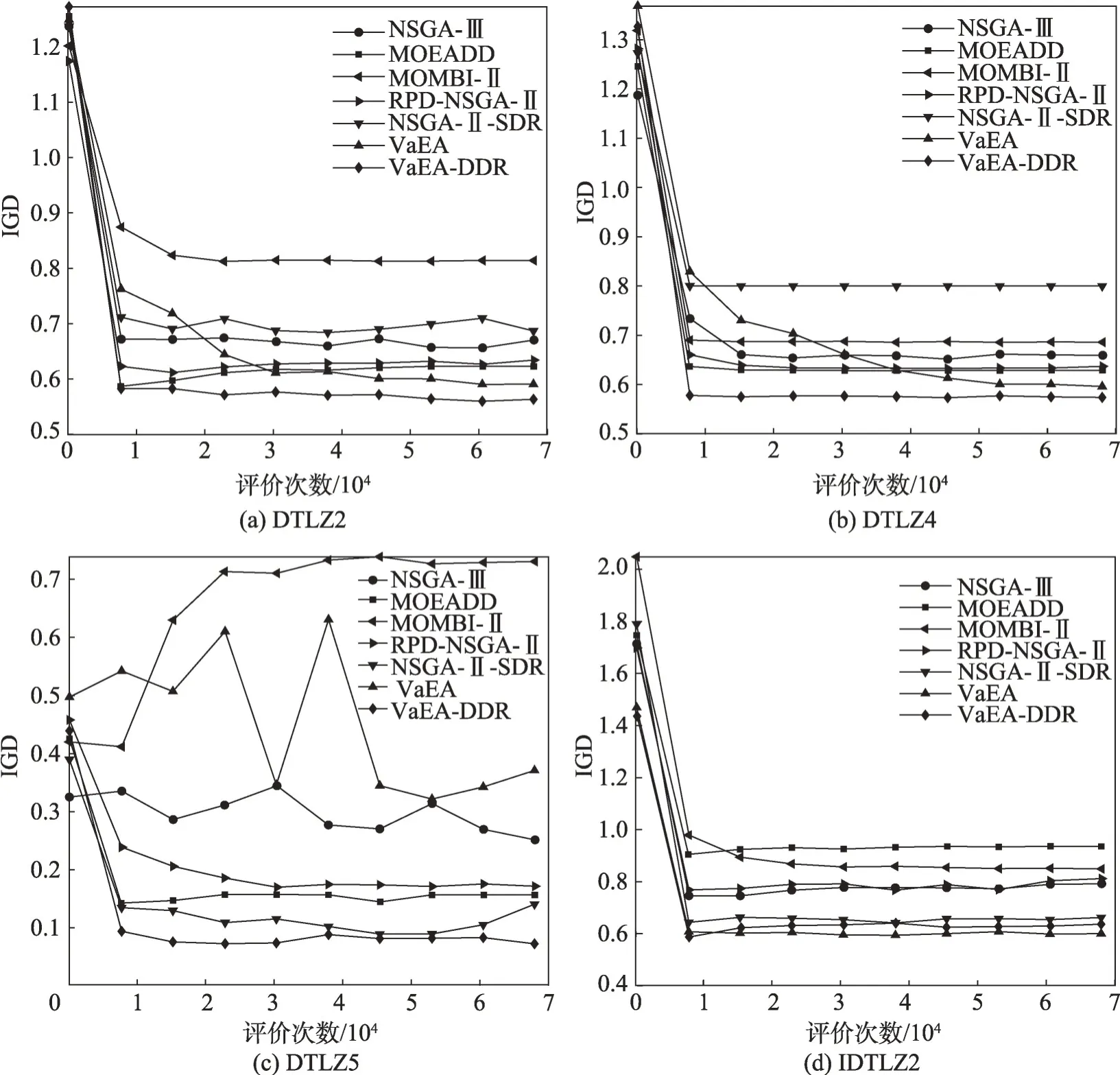
圖4 7種算法在15目標(biāo)上獲得的IGD值變化曲線Fig.4 IGD value change curves of 7 algorithms on 15 objectives

為了檢驗(yàn)提出的距離優(yōu)勢關(guān)系是否能增強(qiáng)VaEA算法多樣性，表4給出了7種算法在5、8、10、15目標(biāo)DTLZ 和IDTLZ 測試問題上獲得的Spread 平均值與標(biāo)準(zhǔn)差。從表4 中可以知道VaEA-DDR 算法具有最佳Spread 值的個(gè)數(shù)為16，相比6 種對比算法具有更優(yōu)Spread 值的個(gè)數(shù)分別為24、24、27、28、21、10。由此可知距離優(yōu)勢關(guān)系顯著增強(qiáng)了VaEA 算法多樣性。

為了檢驗(yàn)距離優(yōu)勢關(guān)系能否有效保證算法的收斂性，表5 對VaEA 與VaEA-DDR 算法的GD 值進(jìn)行對比。從表中可以看出，改進(jìn)后的VaEA-DDR 算法在DTLZ1、DTLZ4 與IDTLZ1 問題上表現(xiàn)出絕對優(yōu)勢，VaEA 算法僅在15 目標(biāo)DTLZ2，5 目標(biāo)與8 目標(biāo)DTLZ3 和DTLZ5 以及IDTLZ2 測試問題上比VaEADDR 具有更好的GD 值。這說明距離優(yōu)勢關(guān)系并沒有削弱算法的收斂性，在DTLZ1 問題上可以明顯看出，距離優(yōu)勢關(guān)系有效增強(qiáng)了算法的收斂性。

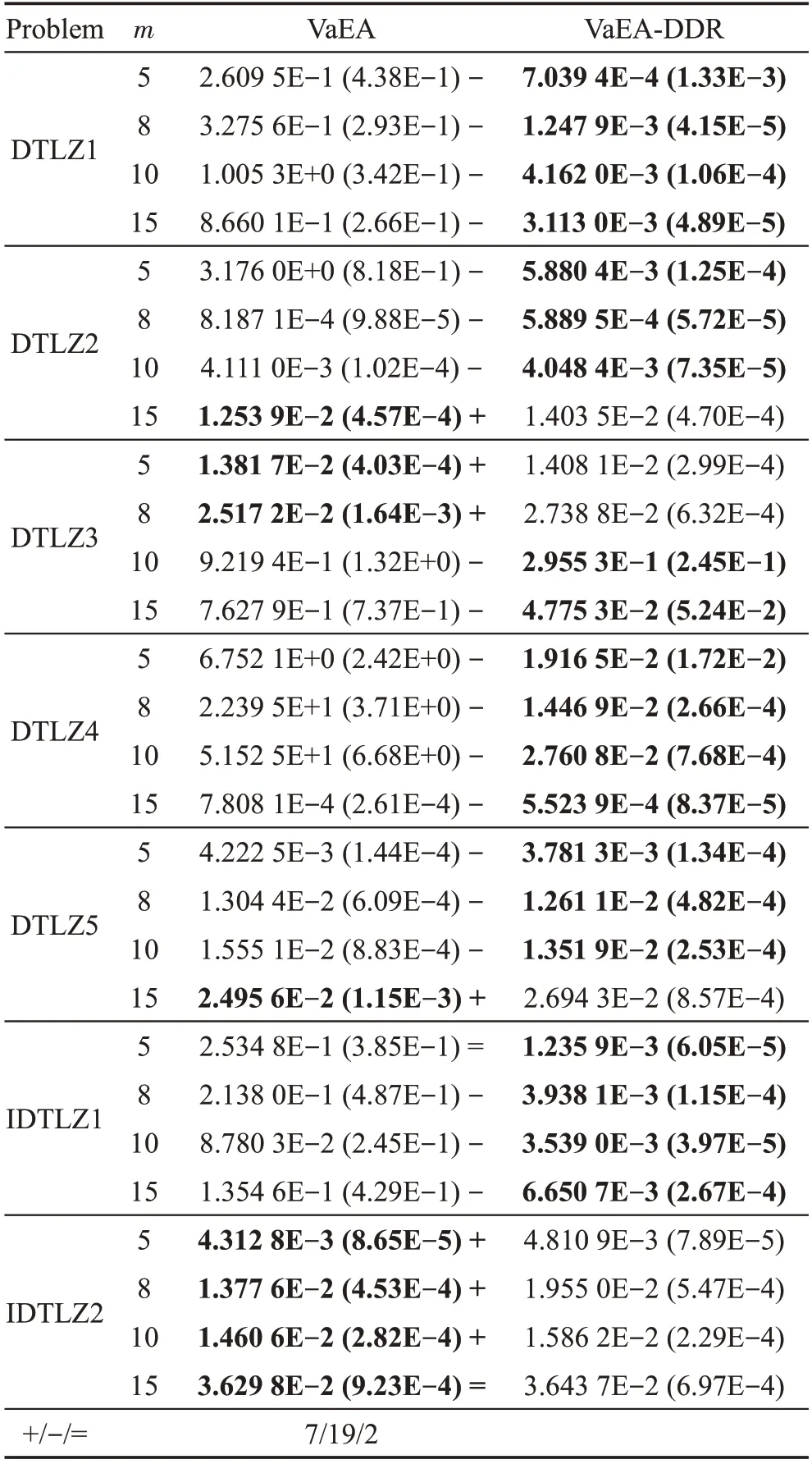
表5 VaEA與VaEA-DDR算法GD值對比Table 5 Comparison of GD values between VaEA and VaEA-DDR algorithms

綜上所述，本文提出的距離優(yōu)勢關(guān)系極大提升了VaEA算法求解高維多目標(biāo)問題上算法的多樣性，在增強(qiáng)算法多樣性的同時(shí)有效維護(hù)了算法的收斂性。

3.5 汽車碰撞測試實(shí)驗(yàn)的實(shí)際應(yīng)用

為了驗(yàn)證改進(jìn)后的算法在實(shí)際應(yīng)用上的求解性能，在經(jīng)典的高維多目標(biāo)汽車碰撞的實(shí)際問題[17]上對算法性能進(jìn)行測試。汽車碰撞問題為9 目標(biāo)測試問題，決策變量的個(gè)數(shù)為11個(gè)，包括汽車相關(guān)構(gòu)件的厚度、材料性質(zhì)等。最大的迭代次數(shù)為800 次，種群大小設(shè)置為11d-1，d為決策變量數(shù)量。在實(shí)際問題上運(yùn)行20 次得到的IGD 與HV 平均值用來評估實(shí)驗(yàn)結(jié)果。注意，計(jì)算IGD值時(shí)，所有算法得到的非支配集作為參考集；計(jì)算HV 時(shí)，所有算法得到的非支配集的最差目標(biāo)函數(shù)加上一個(gè)小閾值作為參考點(diǎn)。表6 給出了7 種算法在實(shí)際問題上獲得的IGD 和HV值。從實(shí)驗(yàn)結(jié)果看，改進(jìn)后的算法獲得了最佳的IGD和HV值，相比原算法有一定的提升。這說明在實(shí)際問題上，使用距離優(yōu)勢關(guān)系改進(jìn)后的算法仍能具備良好的求解性能。

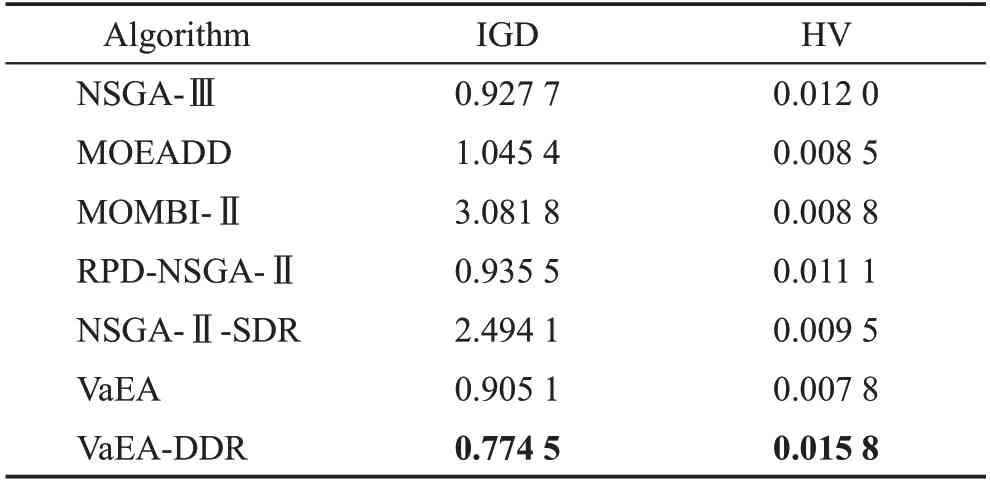
表6 7種算法在汽車碰撞實(shí)驗(yàn)獲得的IGD與HV值Table 6 IGD and HV values obtained by 7 algorithms in car crash experiment

3.6 距離優(yōu)勢關(guān)系適用性驗(yàn)證

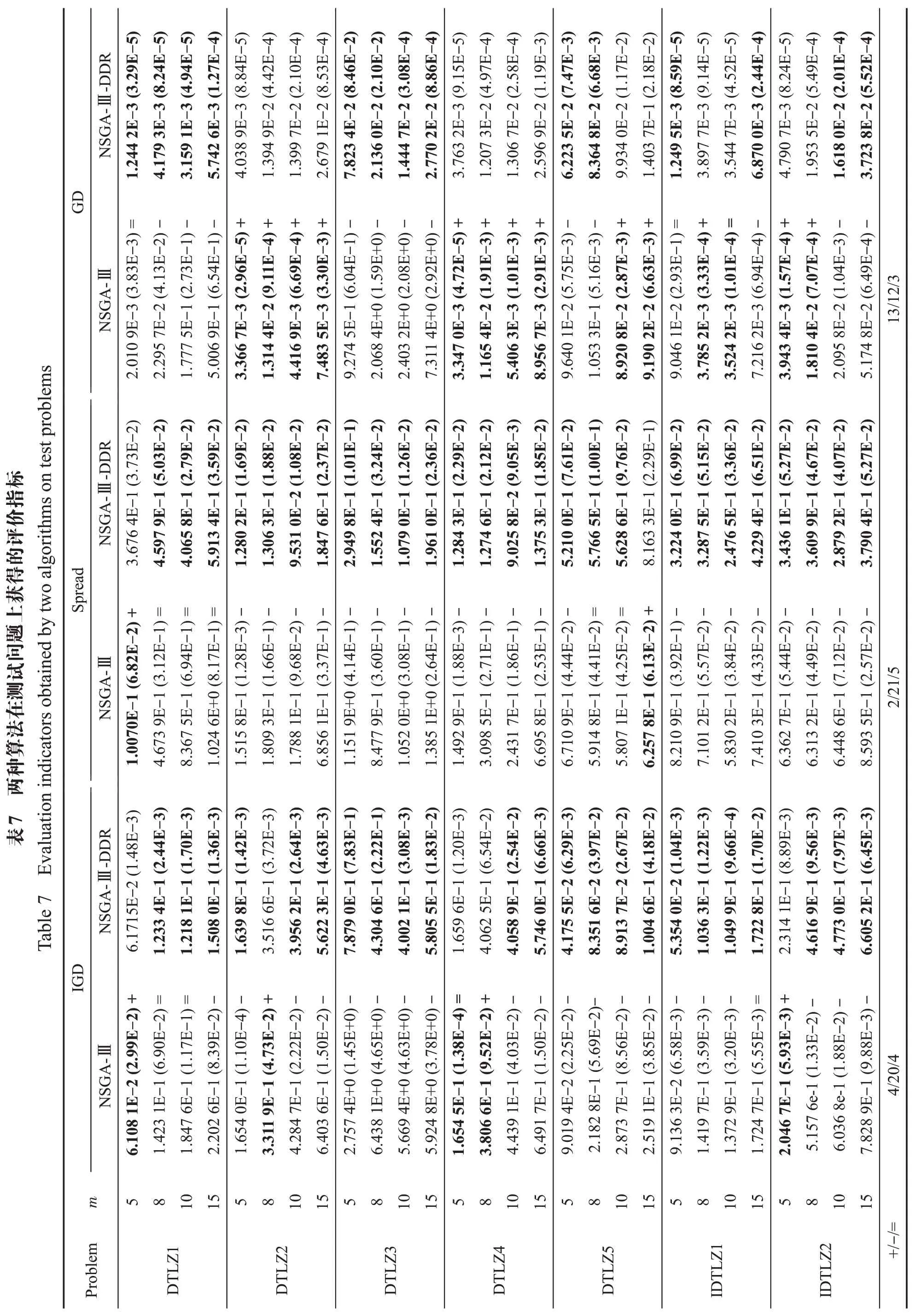
為了驗(yàn)證所提出的距離優(yōu)勢關(guān)系的適用性，本節(jié)給出了結(jié)合距離優(yōu)勢關(guān)系改進(jìn)的NSGA-Ⅲ算法的實(shí)驗(yàn)對比。表7 給出了NSGA-Ⅲ與NSGA-Ⅲ-DDR算法在PlatEMO 平臺獨(dú)立運(yùn)行30 次后得到的IGD值、Spread值以及GD值。

從表7 中可以知道，改進(jìn)后的NSGA-Ⅲ-DDR 算法具有最優(yōu)的IGD值、Spread值以及GD值最佳的個(gè)數(shù)為23、26、15。尤其是從Spread 值上可以看出，改進(jìn)后的NSGA-Ⅲ-DDR 算法基本上都具有最佳值，NSGA-Ⅲ算法僅在5目標(biāo)的DTLZ1問題與15目標(biāo)的DTLZ5 問題上具有更優(yōu)的Spread 值，這再次驗(yàn)證了距離優(yōu)勢關(guān)系能顯著提升算法的多樣性。同時(shí)，從GD 值上可以看出，兩種算法均具有一半的最優(yōu)值，這說明了距離優(yōu)勢關(guān)系能有效保證算法的收斂性。綜合上述分析，說明了距離優(yōu)勢關(guān)系對NSGA-Ⅲ算法的性能同樣有提升，具有較強(qiáng)的適用性。

4 結(jié)束語

為了增強(qiáng)算法在高維目標(biāo)空間的多樣性，本文提出了一種距離優(yōu)勢關(guān)系。首先，通過計(jì)算候選解到理想點(diǎn)的距離作為適應(yīng)度值選擇更優(yōu)解，能保證求解過程中算法的收斂性。其次，通過構(gòu)建的小生境選擇技術(shù)，保證了在同一小生境內(nèi)只保留一個(gè)最優(yōu)解，能在非支配排序階段有效加強(qiáng)算法的多樣性。基于所提出的優(yōu)勢關(guān)系對VaEA算法進(jìn)行改進(jìn)，在DTLZ 與IDTLZ 測試問題上進(jìn)行對比實(shí)驗(yàn)。從實(shí)驗(yàn)結(jié)果可以知道，改進(jìn)的VaEA-DDR 算法取得最佳IGD 值與Spread 值的個(gè)數(shù)分別為16、16，并且在多樣性方面具有顯著性優(yōu)勢。同時(shí)在NSGA-Ⅲ算法上驗(yàn)證了所提出距離優(yōu)勢關(guān)系的適用性，實(shí)驗(yàn)結(jié)果表明本文提出的距離優(yōu)勢關(guān)系具有良好的適用性。在汽車碰撞實(shí)驗(yàn)中，改進(jìn)后的算法能取得最優(yōu)的表現(xiàn)，這說明使用距離優(yōu)勢關(guān)系改進(jìn)的算法能應(yīng)用于實(shí)際問題求解。

雖然從實(shí)驗(yàn)結(jié)果來看距離優(yōu)勢關(guān)系對算法的性能有較大提升，但是目前算法不能非常有效區(qū)分依據(jù)距離優(yōu)勢關(guān)系劃分的非支配層級。在后續(xù)的研究過程中可以進(jìn)一步完善研究算法的選解過程，提升距離優(yōu)勢關(guān)系的適應(yīng)性。