思想引領 感悟方法 學會思考
——以2022年新高考I卷第18題為例
張文海
(江蘇省蘇州實驗中學 215151)
2022年全國高考的大幕已經落下,但它給我們留下了很多的思考,也給我們今后的教學指引了方向.從學生考后的反應來看,普遍覺得新高考數學I卷整體難度較大,主要體現在思維能力要求高、運算能力要求強.哪怕在一些常規知識版塊,如第18題三角題,一些學生由于在平時復習中只是一味地刷題,而不注重從思想上感悟解題方法,導致在考場上無從下手,或者未能快速準確地解答,給學生的考試心理造成了很大的困擾,影響了整場考試水平的發揮.
能夠在限定的時間內快速地找到解題突破口,需要我們在平時的復習中注意分析條件和結論之間的聯系,在思想的引領下整體把握問題,理解問題的本質,在一般思維方法引導下尋找解題思路,才能提升自己分析問題、解決問題的能力,真正提高自己的數學素養.[1]

分析 此題是解三角形的綜合題,雖然條件簡潔、問題明確,但涉及的知識點較多,有正弦定理、余弦定理、兩角和差公式、倍角公式、基本不等式的應用等,主要考查學生對條件的分析轉化能力、合理選用公式的能力、推理論證的能力.
1 方程思想
方程思想是指從分析問題的數量關系入手,將問題中的已知量和未知量之間的數量關系通過適當設元建立起方程(組),然后通過解方程(組)使問題得到解決的思維方式.
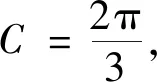
2 轉化化歸思想
轉化化歸思想就是將數學命題由一種形式向另一種形式變換,把待解決的問題通過某種轉化過程歸結為一類已經解決或比較容易解決的問題.轉化與化歸的思想是中學數學最基本的思想方法,堪稱數學思想的精髓所在,常包括抽象轉化為具體、復雜轉化為簡單、未知轉化為已知,通過變換迅速而合理地尋找和選擇問題解決的途徑和方法.
2.1 “角”間轉化
本題題干條件(*)中出現的是2B,而第(1)題要求的是B的大小.從轉化思想的角度,我們就應該想到利用二倍角公式將2B轉為B,再根據式子的結構逆用兩角差的余弦公式進行化簡即可.
2.2 “名”間轉化

2.3 “邊角”間轉化
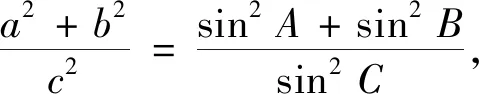
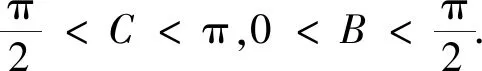
3 減元思想
減元思想是指減少問題中變量的個數,將多元變量問題轉化為一元變量問題,其實質是轉化與化歸思想.最值問題常見的處理方法有幾何法和代數法,解答題常用代數法,包括函數法和不等式法.第(2)題通過邊角轉化后,化為關于角的函數最值問題,目標函數包含三個變量A,B,C,變量個數偏多,從減元思想的角度出發,只要找到幾個變量間的關系,將三元函數減為一元函數,就可以解決問題.
3.1 根據“角”之間的關系減元
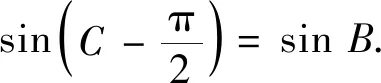
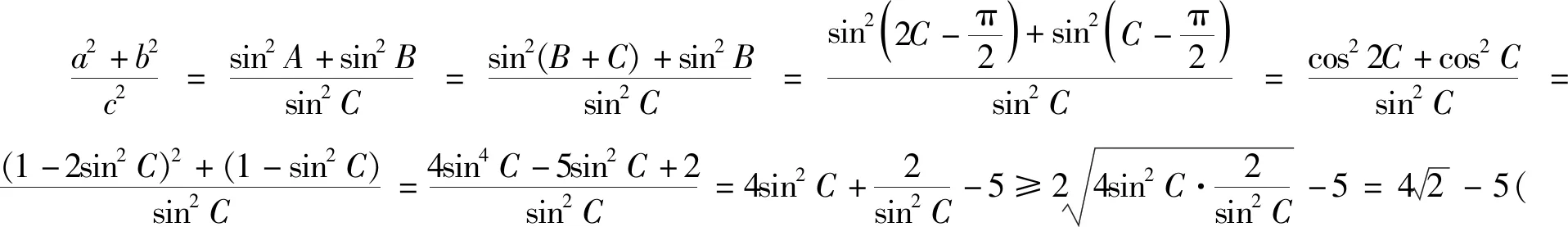
3.2 根據“函數值”之間的關系減元
目標式中涉及三個變量sinA,sinB,sinC,要想將它們減元到一個變量,除了尋找三個角A,B,C之間的關系外,也可以直接尋找sinA, sinB,sinC之間的關系式,然后進行減元處理.
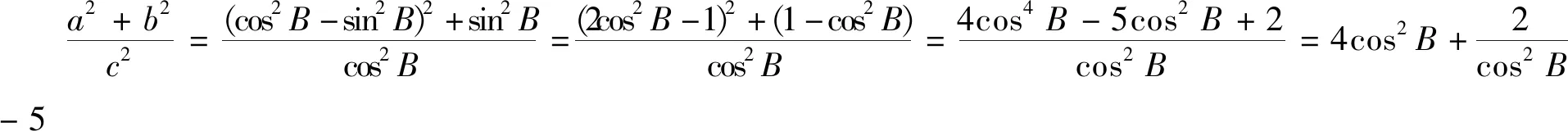
4 數形結合思想
數形結合思想注重“數”與“形”結合,相互滲透,把代數式的精確刻劃與幾何圖形的直觀描述相結合,使代數問題與幾何問題相互轉化,使抽象思維與形象思維有機結合.應用數形結合思想,就是充分考查數學問題的條件與結論之間的內在聯系,既分析其代數意義又提示其幾何意義,將數量關系和空間形式巧妙結合,尋求解題思路,使問題得到快速解決.
4.1 構造直角三角形,尋找邊角關系
高中學習了正余弦定理之后,我們運用定理可以處理斜三角形的問題,但如果在其中特殊的三角形——直角三角形中,尋找邊角之間的關系會更為簡便,故從數形結合思想的角度聯想可以構造直角三角形,幫助我們快速尋找邊角間的關系式.
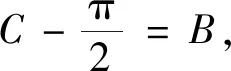

圖1
4.2 利用相似三角形,尋找邊間關系
由兩個三角形相似可以得到邊之間的比例關系,從而據此可以進行邊之間的轉化和化歸,減少變量的個數,將復雜問題轉化為簡單問題處理.

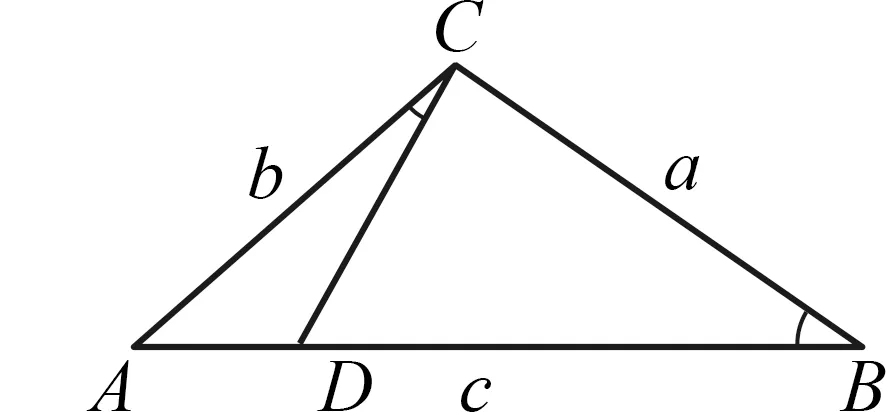
圖2
本題中的三角形可以構造子母三角形,此類模型在2021年全國I卷第19題曾經考查過.這就要求我們在高三數學復習教學中,對于經典高考試題要舍得花時間去研究,要抓住問題本質特征,提煉數學思想,感悟數學方法,方能觸類旁通,舉一反三.
(2021年全國I卷19題)記△ABC的內角A,B,C的對邊分別為a,b,c.已知b2=ac,點D在邊AC上,BDsin∠ABC=asinC.(1)證明:BD=b;(2)若AD=2DC,求cos∠ABC.
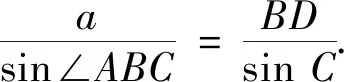
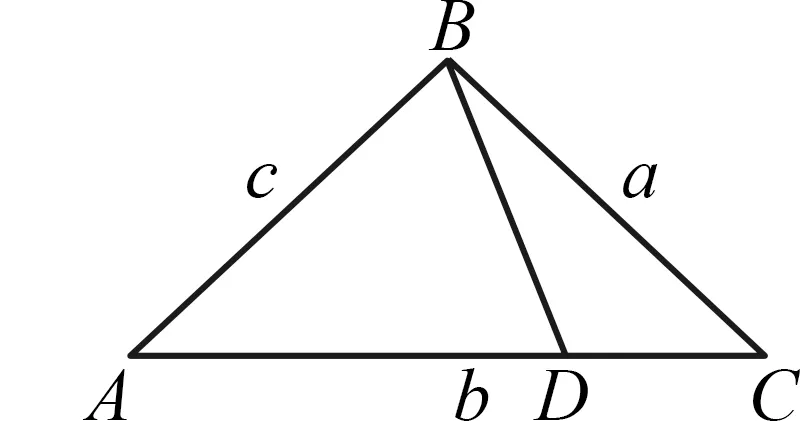
圖3

5 反思與啟示
本題蘊含了多種數學思想方法,從不同的思想視角出發,可以尋找到不同的處理方法,對學生來講就是一種數學能力和內隱的數學素養.要想讓學生在考場上站得高、看得遠,就需要我們在平時的教學中緊緊圍繞數學思想,引導學生根據問題的具體結構,全方位、多角度地觀察和理解問題,通過數學思想來溝通知識間的聯系,進行有效追問,揭示問題、方法的本質,追求一般的思維方法,挖掘方法背后的思想,發揮思想的統領作用,最終使學生能夠從數學思想方法的視角出發,分析和解決問題,并使之成為學生思考和解決問題的一種自覺習慣.[2]
教育部考試中心主編的《高考數學測量理論與實踐(2007年版)》,針對高考對學生理解數學思想方法及應用能力的考查要求,對中學比較重要的思想和方法進行了層次劃分和系統歸類,將數學思想和方法分為三大類.第一類:數學思想方法,主要包括函數與方程的思想、數形結合的思想、分類與整合的思想、轉化與化歸的思想、特殊與一般的思想、有限與無限的思想、或然與必然的思想、算法的思想.這些都是高考必考的重要數學思想方法.第二類:數學思維方法,主要包括分析法、綜合法、歸納法、演繹法、觀察法、實驗法、特殊化方法等.第三類:數學方法,主要指應用面較窄的具體方法,如配方法、換元法、待定系數法等具體的解題方法.[3]這三類之間的關系可以用這樣一句話概括,就是在問題解決過程中人們利用第二類數學思維方法,在第一類數學思想方法的指引下采用第三類具體的數學方法解決問題.簡單來說,方法是“術”,思想是“道”!思想是方法的上位,具有指導意義.
在解題過程中要突出以數學思想方法為指導,分析和研究問題,充分發揮數學思想方法對發現解題途徑的定向、聯想和轉化功能.[4]在解題過程中或者解題結束后還要不斷地總結、歸納解題方法,并加以提煉上升到數學思想的高度,這一過程學生很難自發實現,需要教師的引導和幫助.這也正好體現新課程標準所提出的教師是引導者、合作者的角色.

