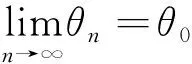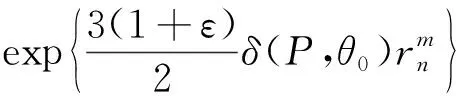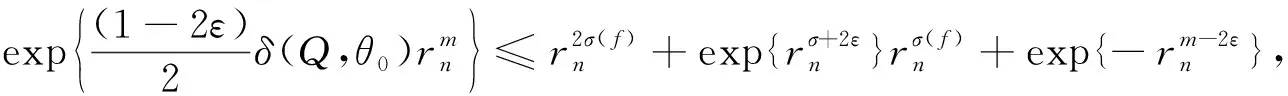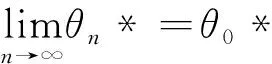二階非齊次線性微分方程解的增長性
徐曉妍,肖麗鵬
(江西師范大學數學與統計學院,江西 南昌 330022)
1 引言和結果
在本文中將使用亞純函數值分布理論中的標準符號{1,2},使用σ(f)表示亞純函數f(z)的增長級,定義為
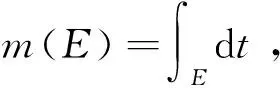
考慮微分方程
f''+e-zf'+Q(z)f=0
解的增長級,其中Q(z)是一個有限級整函數。
Gundersen對于Q(z)是一個超越整函數的情況證明了
定理A[3]若Q(z)是一個超越整函數σ(Q)≠1, 那么方程f''+e-zf'+Q(z)f=0的所有非零解都是無窮級的。
那么在這種情況下就產生了一個問題,方程f''+P(z)f'+Q(z)f=0的系數滿足什么條件時,方程解的增長級才是無窮呢?陳宗煊研究了方程f''+A1(z)eazf'+A0(z)ebzf=0解的增長性,得到了
定理B[4]設Aj(z)(?0)是整函數且σ(Aj)<1,(j=0,1),a,b為復常數且滿足ab≠0和a=cb(c>1),那么方程
f''+A1(z)eazf'+A0(z)ebzf=0
的所有非零解都是無窮級的。
同時他還提出
定理C[4]假設a,b是非零復常數且a≠b,Q(z)是非常數多項式或Q(z)=h(z)ebz,h(z)是非零多項式。那么方程f''+eazf'+Q(z)f=0的每個非零解f都是無窮級的且σ2(f)=1。
在得到了定理B的結果后,陳宗煊研究了方程f''+(A1(z)eaz+D1)f'+(A0(z)ebz+D0)f=0解的增長性,得到了
定理D[4]設Aj(z)(?0),Dj(z),(j=0,1)是整函數且σ(Aj)<1,σ(Dj)<1,a,b為復常數且滿足ab≠0且arga≠argb或a=cb(0 的所有非零解都是無窮級的。 以上結果都是針對一些齊次線性微分方程得到的,那么當方程為非齊次線性微分方程時,在什么條件下方程的解均為無窮級呢?王珺在[5]中給出以下結果。 定理E[5]設Aj(z)(?0),(j=0,1),H是整函數且σ(Aj)<1,σ(H)<1,a,b為復常數且滿足ab≠0和a≠b,那么方程 f''+A1(z)eazf'+A0(z)ebzf=H(z) 的所有非零解都是無窮級的。 f''+(A1(z)eaz+D1)f'+(A0(z)ebz+D0)f=H(z) 的所有非零解都是無窮級的。 用多項式去替代定理E和定理F中的az和bz,方程系數滿足什么條件時,方程解的增長級均為無窮呢?本文研究了這個問題并得到了以下結果。 定理1設Ak(z)(?0),(k=0,1),H是整函數,m(≥1)為整數且σ(Ak) f''+A1(z)eP(z)f'+A0(z)eQ(z)f=H(z) (1.1) 的所有非零解都是無窮級的。 f''+(A1(z)eP(z)+D1)f'+(A0(z)eQ(z)+D0)f=H(z) (1.2) 的所有非零解都是無窮級的。 引理2.1[6]g(z)是有限級整函數,用νg(r)表示g的中心指標,則有 引理2.2[7]設n≥2,fj(z)(j=1,…,n)是亞純函數,gj(z)(j=1,…,n)是整函數滿足 (ⅱ)當1≤j≤k≤n時,gj(z)-gk(z)不是一個常數; (ⅲ)E?(1,∞)是對數測度為有限的集合,當1≤j≤n,1≤h≤k≤n時,T(r,fj)=o(T(r,egh-gk)),(r→∞,r?E),那么fj(z)≡0(j=1,…,n)。 (2.1) e-5πM(r,f)1-C(σ,ζ)≤|f(reiθ)| (2.2) (2.3) 引理2.6[9]設P(z)=(α+iβ)zn+…(α,β是實數,|α|+|β|≠0)為多項式且次數n≥1。A(z)(≡0)為整函數且σ(A) (ⅰ)若δ(P,θ)>0, 則 exp{(1-ε)δ(P,θ)rn}<|g(reiθ)| (2.4) (ⅱ) 若δ(P,θ)<0, 則 exp{(1+ε)δ(P,θ)rn}<|g(reiθ)| (2.5) 其中H2={θ:θ∈[0,2π),δ(P,θ)=0}為有限集。 引理2.7[10]設f(z)是超越亞純函數且σ(f)=σ<∞,H={(k1,j1),…,(kq,jq)}是由不同整數對組成的有限集,且滿足ki>ji≥0(i=1,2,…,q),又設ε>0是任意給定的常數,則 (ⅰ)存在零測度集E1?[0,2π),滿足若φ∈[0,2π)E1,則存在常數R0=R0(φ)>1滿足對所有的argz=φ和|z|≥R0的z及對所有(k,j)∈H都有 (2.6) (ⅱ)存在對數測度為有限的集合E2?(1,∞),使得對滿足|z|?E2∪[0,1]的所有z以及對所有(k,j)∈H仍有(2.6)成立。 (ⅲ)存在測度為有限的集合E3?[0,∞)使得對滿足|z|?E3的所有z以及對所有(k,j)∈H都有 (2.7) 成立。 假設f(z)是方程(1.1)的非零解且σ(f)<∞,我們可以斷言σ(f)≥m。若σ(f) (3.1) (3.2) 成立。根據中心指標的定義知,當r→∞時,νf(r)→∞。由引理2.1知,當r充分大時,有 νf(r)≤rσ(f)+1 (3.3) 由引理2.7中的(ⅱ)知,對所有z滿足|z|=r?E2∪[0,1],其中E2是一個對數測度有限的集合,有 (3.4) (3.5) e-5πM(r,f)1-C≤|f(reiθ)| (3.6) 下面我們將分3種情形討論。 情形1若δ(P,θ0)>0,由δ(P,θ)的連續性知,對充分大的n有 (3.7) 結合引理2.6中的(2.4)知,對充分大的n有 (3.8) 由(3.1)可以得到 (3.9) 下面把情形1分成3種子情形討論。 情形1.1設θ0滿足η=δ(Q-P,θ0)>0,由δ(Q-P,θ)連續性可知,對充分大的n有 同理由引理2.6對充分大的n有 (3.10) 把(3.2),(3.3)和(3.5)代入(3.9)中,對充分大的n有 (3.11) 結合(3.8)得 (3.12) 由(3.3),(3.10)和(3.11)有, 矛盾。 情形1.2設θ0滿足η=δ(Q-P,θ0)<0,由δ(Q-P,θ)連續性和引理2.6知,對充分大的n有 (3.13) 可以注意到此時仍有(3.11)和(3.12)成立,由(3.11)-(3.13)可知,當n→∞時有 即有 這說明當n→∞時,vf(rn)→0,矛盾。 η=δ(Q-P,θ)>0, η=δ(Q-P,θ)<0, 和 (3.14) 成立。由引理2.5的證明過程,易知M(rn,f)≥ (3.15) 取l0充分小,由δ(P,θ)的連續性有δ(P,θ0*)>0,那么就有 (3.16) 把(3.4)和(3.15)代入(3.9)中可得, 再結合(3.14)和(3.16)可以得到, 矛盾。 (3.17) 由(3.1)知當n→∞時, (3.18) 仍把情形2分成3種子情形說明。 (3.19) 將(3.2),(3.4),(3.5)和(3.17)代入(3.18)中得 (3.20) 再由(3.4)和(3.19)知, 矛盾。 (3.21) 由(3.18)得,當n→∞時,有 把(3.2),(3.4),(3.5),(3.17),(3.21)代入上式中,當n→∞時,有 這說明當n→∞時,νf(rn)→0,矛盾。 對于充分大的n, 矛盾。 情形3若δ(P,θ0)=0, 此時再對δ(Q,θ0)的情況進行討論。 矛盾。 情形3.2若δ(Q,θ0)<0,由引理2.6中δ(P,θ)的定義,當P(z)=(α+iβ)zm+…時可以定義 由于am≠0,則δ'(P,θ0)≠0,取點列{zn'=rneiθn'}滿足0<|θn'-θn| (3.22) 由引理2.6即可知,對充分大的n有 (3.23) (3.24) 由(3.4),(3.15),(3.22)-(3.24)知, 上是任意取的,對充分大的rn,由上式可以得到, (3.25) 其中η1(θ)=(1-2ε)δ'(P,θ),η2(θ)=(1-2ε)δ(P,θ)。 對所有的θ∈(θ0,θ0+l0)都有δ(P,θ)>0,因此有 (3.26) 用logf(rneiθ0)來表示對數函數logf(rneiθ)的主值即0≤arglogf(z)≤2π,由于 當rn充分大時,由上式得 log|f(rneiθ)|+2π≥|logf(rneiθ)|≥ 即有log|f(rneiθ)|≥log|f(rneiθ0)|-4π-ξ(rn,θ) (3.27) exp{-(1-2ε)δ(P,θn*)rn} (3.28) 矛盾。 當c<0時,取足夠小的l0使得當θ∈(θ0,θ0+l0)或θ∈(θ0-l0,θ0)時,有δ(Q,θ)<0<δ(P,θ)類似于情形3.2,有(3.25),(3.27),(3.28)成立。Wiman-Valiron理論知,當n→∞時,νf(rn)→0,矛盾。 當0 當c>1時,取足夠小的l0使得當θ∈(θ0,θ0+l0)或θ∈(θ0-l0,θ0)時,有δ(Q-P,θ)<0<δ(P,θ)成立,并且當θn'∈(θ0,θ0+l0)或(θ0-l0,θ0)時,對點列{zn'=rneiθn'}有(3.15)成立。由(3.1)得 類似于情形3.2,有(3.25),(3.27)成立。同樣當n→∞時,νf(rn)→0,矛盾。 定理1證畢。 假設f是方程(1.2)的非零解且σ(f)<∞,我們可以斷言σ(f)≥m。若σ(f) (4.1) 令σ=max{σ(D0),σ(D1)} Dj(z)≤exp{rσ+ε},(j=0,1) (4.2) 情形1若δ(Q,θ0)<0<δ(P,θ0)由引理2.6和δ(P,θ)與δ(Q,θ)的連續性,當n充分大時有 (4.3) 和 (4.4) 由(4.1)得 (4.5) 由(4.2)-(4.4)知,當n充分大時有 和 將(3.2),(3.4),(3.5)代入(4.5)中,當n充分大時,有 這說明當n→∞時,νf(rn)→0,矛盾。 情形2若δ(P,θ0)<0<δ(Q,θ0),由引理2.6和δ(P,θ)與δ(Q,θ)的連續性,當n充分大時,有 (4.6) 和 (4.7) 由(4.1)即有 (4.8) 結合(4.2),(4.6),(4.7)知當n充分大時,有 和 定理2證畢。
2 證明定理所需引理
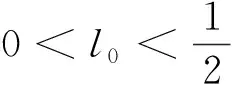
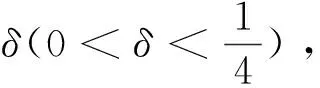
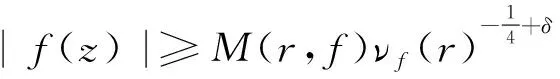
3 定理1的證明
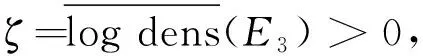
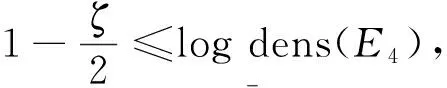
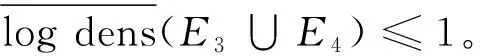

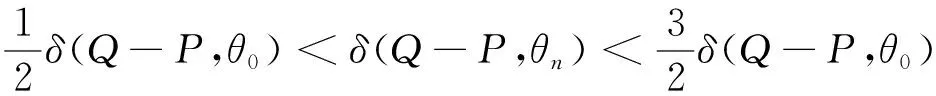
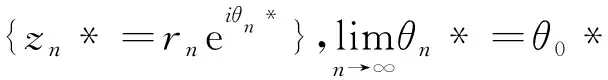
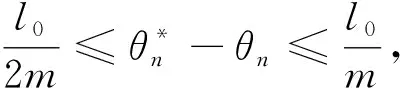
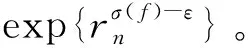
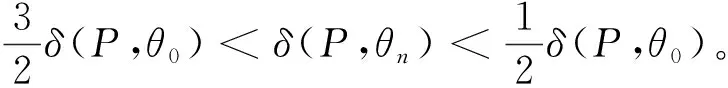
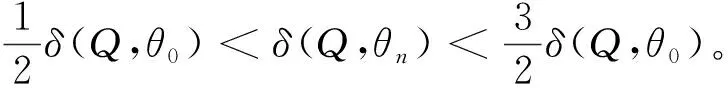
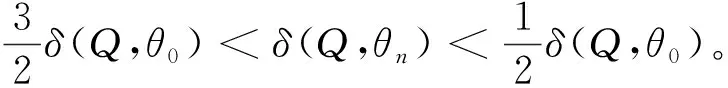
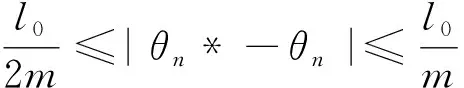
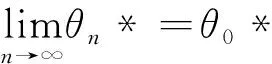
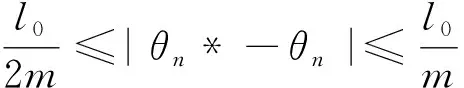
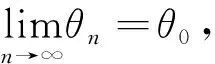
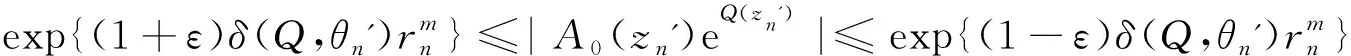
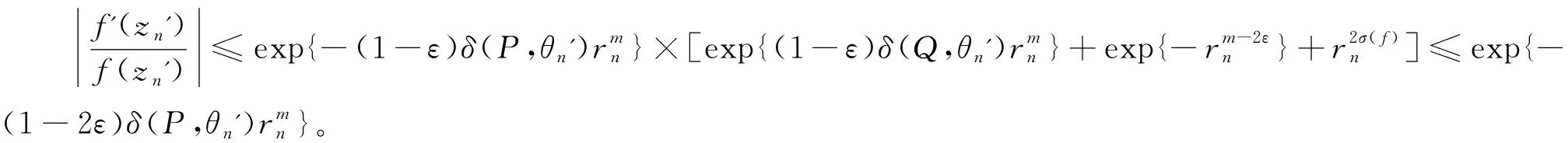
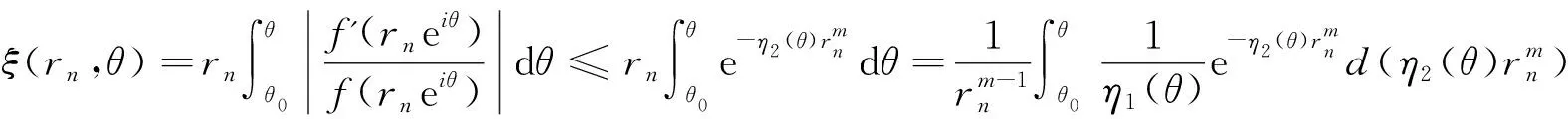
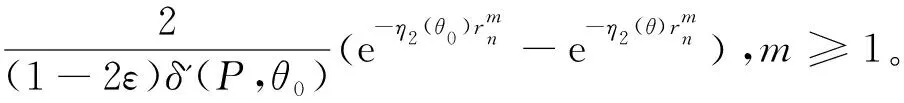
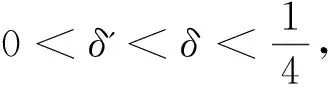
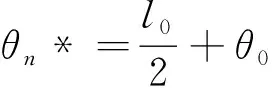
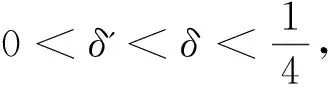
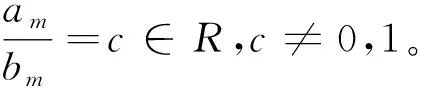
4 定理2的證明