基于變權重組合模型的高速公路路基沉降量預測分析

周智青

(廣西路橋工程集團有限公司，廣西 南寧 530200)

0 引言

高速公路直接帶動了周邊城市發展與經濟建設，是城市與城市之間資源、信息、文化交流交換的紐帶。在高速公路建設過程中，路基是決定公路路面承載能力的關鍵，其質量的優劣直接關系著高速公路行駛車輛的安全。在長期運營過程中，高速公路路面會在載荷剪力作用下出現路面開裂、道路傾斜、局部坍塌等不同程度的問題，其原因在于路基的沉降。為了避免上述問題帶來的安全隱患，能夠在最短時間內獲得精準的路基沉降數據，提高高速公路使用壽命，需要對其進行沉降預測。

由于路基沉降過程受到天氣與人為等多種不確定性因素的影響，在多種因素綜合作用下，不同因素之間相互影響、轉化，無法通過單一因素對其作用進行預測。因沉降量的預測具有一定的復雜性，受到諸多相關科研人員與學者的關注。李亞峰等[1]提出基于改進的集對分析理論的路基沉降組合預測模型；謝杰輝等[2]提出針對濱海高速公路軟基變形規律及沉降預測的應用；呂綠洲等[3]提出高速鐵路路基沉降影響因素分析及模型預測方法研究。眾多學者們通過對不同結構路段路基沉陷規律的分析與總結，將公路路基沉陷形成要素分別對應路基土質結構權重、施工效率權重、路基回填容重權重等4類權重組合的關系，然而這些高速公路沉降預測模型的單一權重組合，很難涵蓋上述一系列權重組合，并且在施工推廣上存在技術下放難度大、精度控制難度高等公開性問題。基于上述原因，提出一種新的、高效的、精準的高速公路沉降預測模型勢在必行。

隨著大數據信息處理技術的高速發展，本文將大數據分析技術中的動態信息分析與多變量組合思想引入高速公路路基沉降預測模型研究當中，根據高速公路路基沉降因素的多元性與不確定性，將傳統因素定權重組合優化為變權重組合，利用變權重因素的時間對應性，實時反映預測量與實際量之間的發展變化與規律，更加準確地對路基沉降量樣本進行函數表達。通過與另外三種預測模型的實例路段路基沉降數據對比，結果表明，基于變權重組合模型的路基沉降預測結果在數值誤差上最小，預測結果的收斂性更好，更加適合路基預測應用的推廣。

1 工程實例分析

根據對我國高速公路路基沉降類型的分析發現，多數沉降屬于路基軟基沉降[4]，基于此類型預測采用限制閾值的權重組合方法對其進行預測分析。

1.1 工程概況

本文預測路基數據選用某高速公路四標段一個典型斷面(k46+ 100)進行分析。該預測路段路基含有部分軟土層，土層之間空隙比均值為1.108，路段包含的十字板強度能夠承載最大剪力為18 kPa，在力學范疇中屬于較差。在路基結構上采用多技術復合施工方案，將粉噴樁固定與堆載預壓進行關聯，二者同時施工完成。其中，粉噴樁長度為6.8 m，樁與樁之間的距離為1.5 m，施工后的路堤整體高度為4.86 m，設計高度為5.6 m。實測時間-沉降曲線如下頁圖1所示。

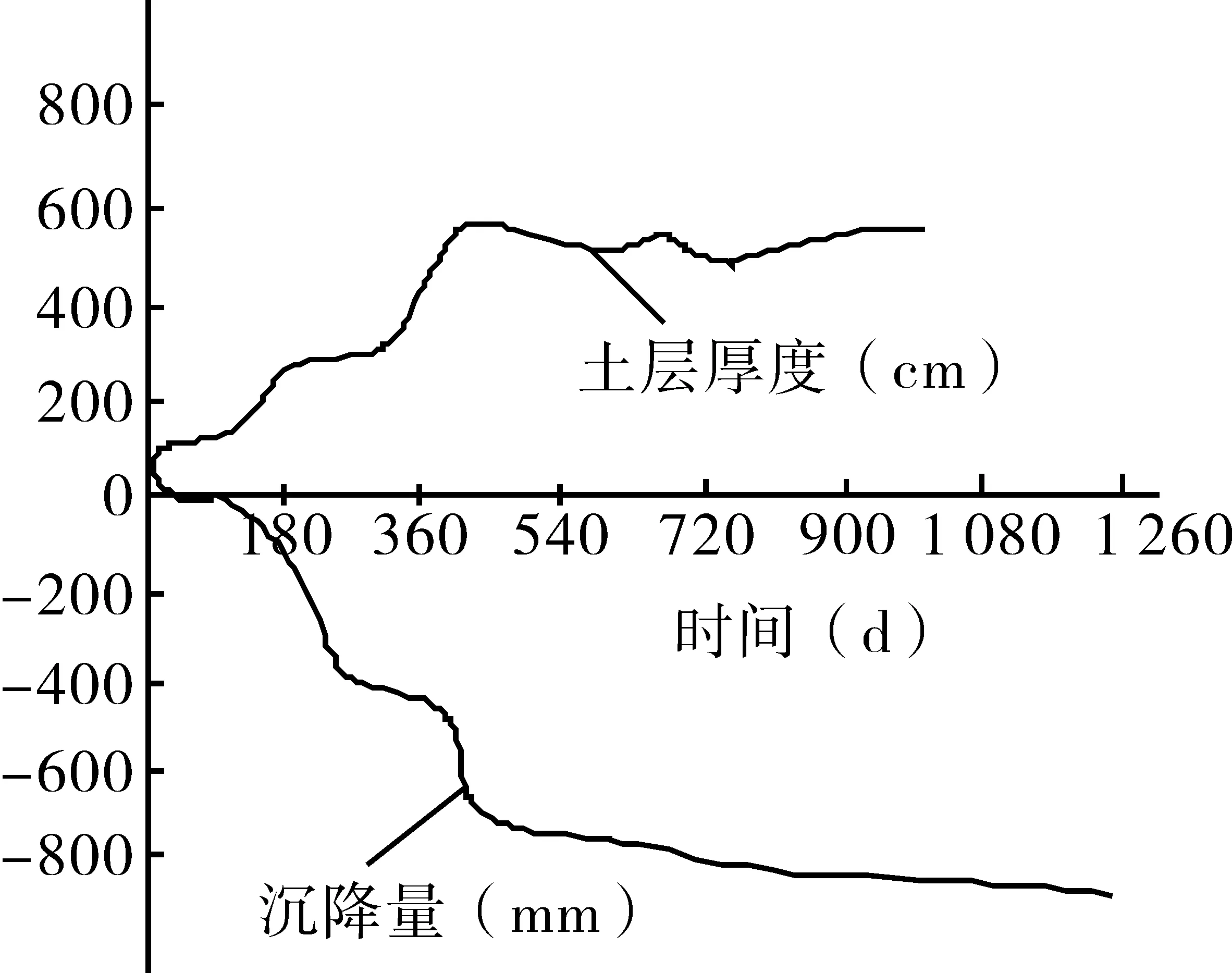
圖1 公路實測時間-沉降曲線圖

1.2 單一權重模型預測

對高速公路相關數據初始信息進行等式轉換，轉換等量系數設定為10[5-7]，在轉換后的數據中，抽取所有滿足堆載預壓期數據，對其進行建模和參數計算。K46+100斷面395～976 d共65個數據，395～586 d對應數據代表堆載預壓期，共計27個數據。對第650～980 d對應的沉降量數據進行預測，預測結果如圖2所示。

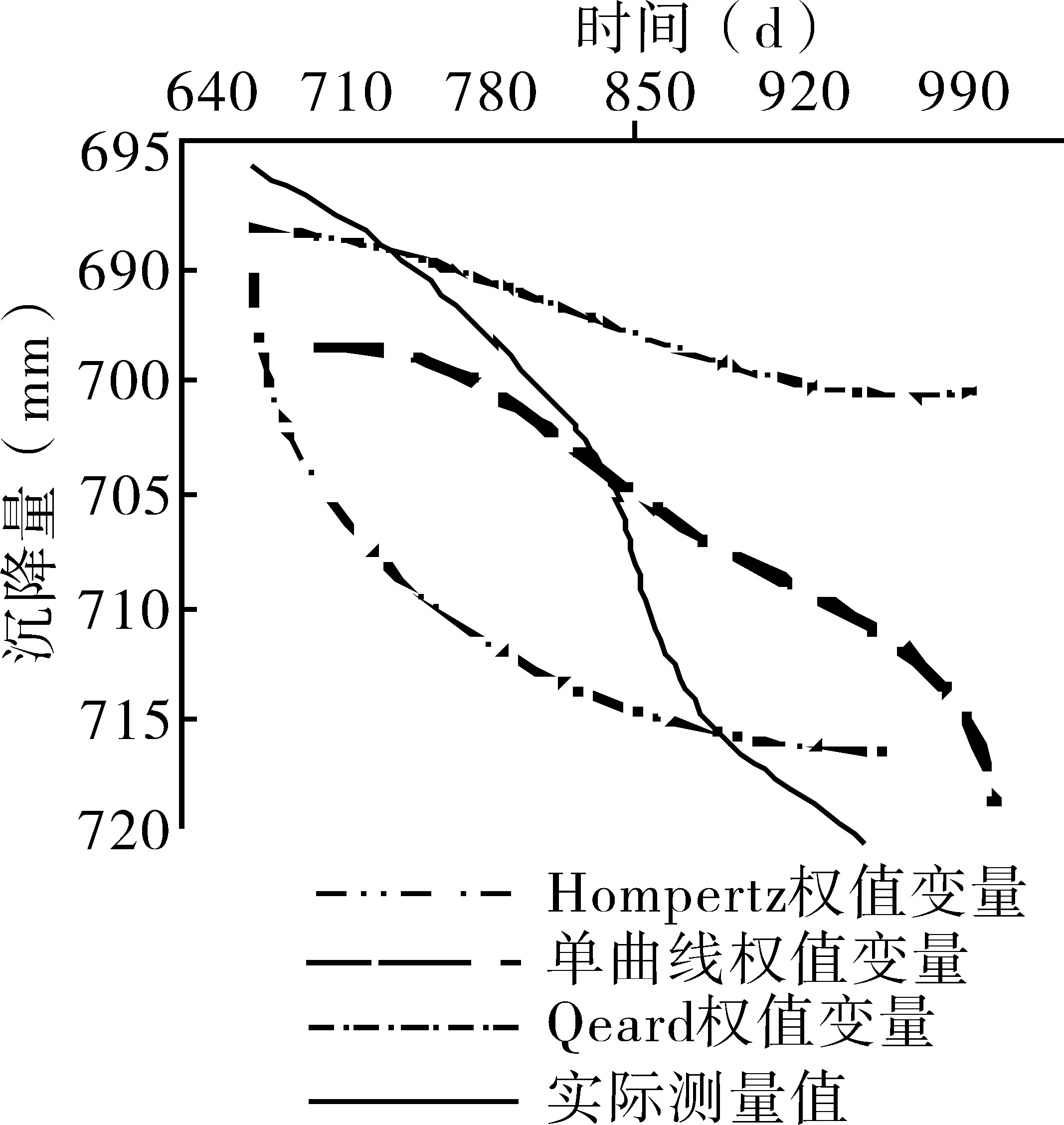
圖2 實際測量值與各種權值變量預測值對比曲線圖

1.3 測試結果

通過對圖2曲線走勢分析可知，三種權值變量對應系數在初期的預測值普遍高于實際測量系數。采用Qeard權值變量與Hompertz權值變量進行高速路徑軟土層工后沉降末期預測時，預測差值較大[8-10]。預測前期各權值變量對應的預測值擬合程度差異較小，隨著時間變量的增加，數據對應的預測變化差異變大，曲線起伏隨之增大，導致預測誤差系數增大，整體權值擬合效果明顯下降，擬合數值普遍減小；除各權值變量預測初期外，單曲線權值預測精準度相較另外兩種權值變量精準度較好，預測曲線整體呈現為“S”形生長。

2 變權重組合模型預測

2.1 變權重組合模型

根據上述工程數據的權重曲線可知，單一權值變量組合方式的不同，其對應的預測結果有所不同。其中，按照權值變量的組合方式可分為定權組合模型和變權組合模型[11]。在變權組合模型中，構成模型的權值系數按照時間變量發展順序進行對應權重組合，以此獲得以時間為依據的權值變量組合函數，對每一時間點的權值預測變化進行相應反映，在時效方面能夠彌補定權組合的不足。當前確定單一權值變量組合方式是建立變權重組合模型的關鍵[12]。

在此之前，有眾多研究人員與相關學者提出多種確定變權重對應權值的方法，而其中多數人認為采用樣本點對應誤差系數最小值為確定準則是最佳解決方案。但是通過多組實踐數據表明，此種方法存在預測結果會隨誤差系數增長而出現異常的問題。此時對求解組合模型的計算難度偏大[13-14]。因此，本文采用樣本點對應誤差系數最小絕對值作為確定準則，以此優化權重系數變量與時間量的對應關系，得到最優正向變權重組合模型：

(1)

其中，上述模型可分為兩種表達形式，分別對應兩種不同的組合情況，具體計算如下：

(1)若位于第k階段m種單一預測權值變量都滿足條件ei，k≥0或ei，k≤0，則對應各單一權值變量位于第k階段的誤差系數均隸屬于同向系數。假設位于第k階段第j種單一權值變量的預測誤差絕對值是其最小系數值，此時對式(1)進行求解計算，可得:

(2)若位于第k階段任意權值系數點的ei，k≥0，其余權值系數點的ei，k≤0，即各單一權值變量的預測誤差互為差異化系數，且屬性互不相同。假設在所有非負誤差系數對應的單一權值變量中，第j1種權值變量組合的預測誤差絕對值最小; 進一步假設在所有負值誤差對應權值變量中，第j2種單一權值變量的預測誤差絕對值最小。則此時對式(1)求解，可得到:

通過上述求解方法可以分別得到不同條件下的單一權值變量在樣本點的組合變權重。

為了更加準確地對公路沉降段進行預測，還需要各單一權值變量在預測點的組合變權重ωi,n+p(i=1，2，…，m;p=1,2,…)。

根據上述兩種求取各單一權值變量在預測點組合變權重的方法，可以推導得到以較少實際樣本數據為實際條件的各單一權值變量在第n+p期的組合變權重，通過計算前n期組合變權重的平均值，來獲得本文所需的變權重組合模型，即:

(2)

2.2 變權重組合模型實例分析

基于變權重組合模型，引入實例數據進行分析。

某高速路基沉降路段的歷史實際測量數據見表1。抽取1～6路段數據作為變權重組合模型的樣本數據，第7路段數據定義為模型預測性能的檢驗數據。

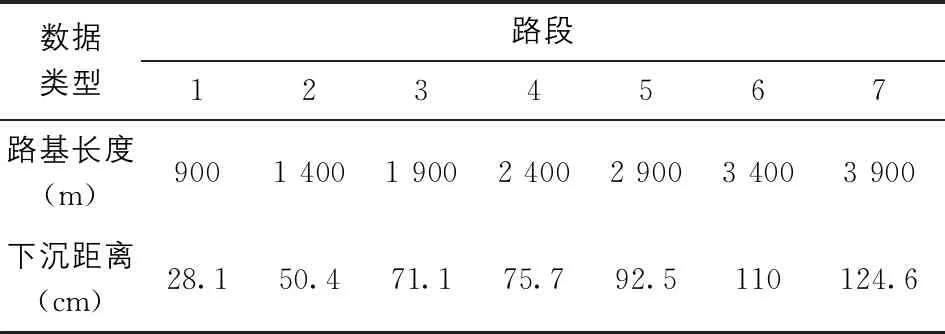
表1 某高速公路路基沉降路段的歷史實際測量數據表

選取表1中第1～6路段數據，作為前文單一權值變量建立模型的基礎數據，同時完成對實際測量公路沉降數據的預測結果(見表2) ，然后通過計算結果得到單一權值變量對應預測模型的不同樣本數據點的預測誤差(見表3)。結合表3數據與計算關系式(1)、式(2)，可進一步計算得到各單一權值變量預測對應的權值組合系數(見表4)。

表2 各權值變量對公路路基沉降的預測結果表

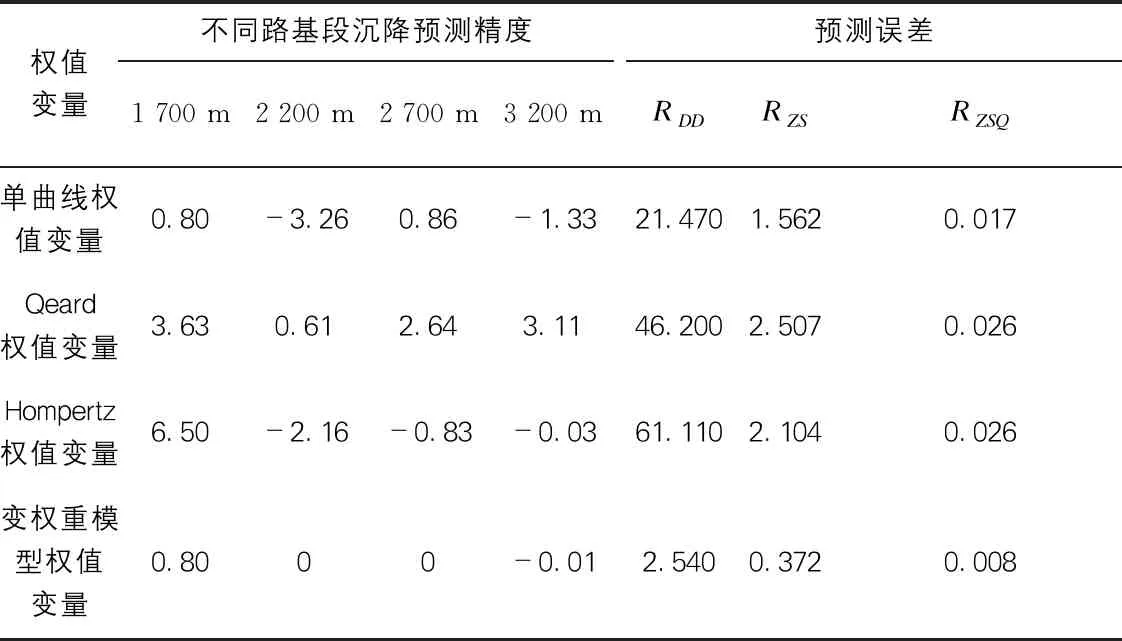
表3 各權值變量的預測精度與預測誤差表

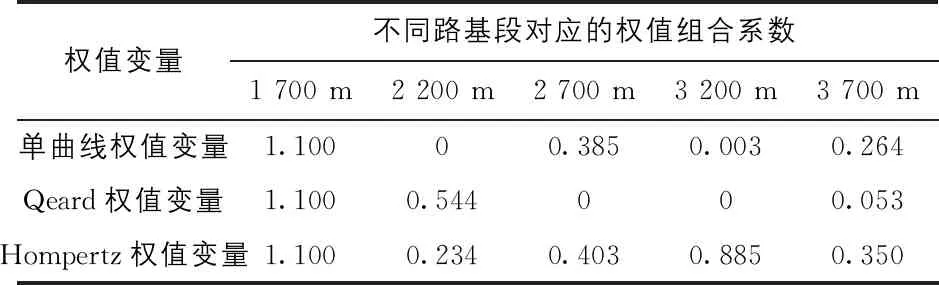
表4 各單一權值變量預測對應的權值組合系數表

考慮到實例數據分析的直觀性，將預測精度判定指標按照組合類別分別對其權重組合模型預測結果的平方系數誤差(RDD)、絕對平均值誤差(RZS)、平均絕對值比值誤差(RZSD)進行計算，計算結果如表3所示。其中，計算值越小對應指標值越小，代表的權重組合模型預測精準度越高。

3 試驗結果分析

3.1 沉降預測誤差對比

依照前文直觀性的設計標準，根據不同預測模型測量結果，將其與實際測量值共同轉換為不同權值變量的高速公路路基沉降預測結果對比曲線圖，如圖3所示。

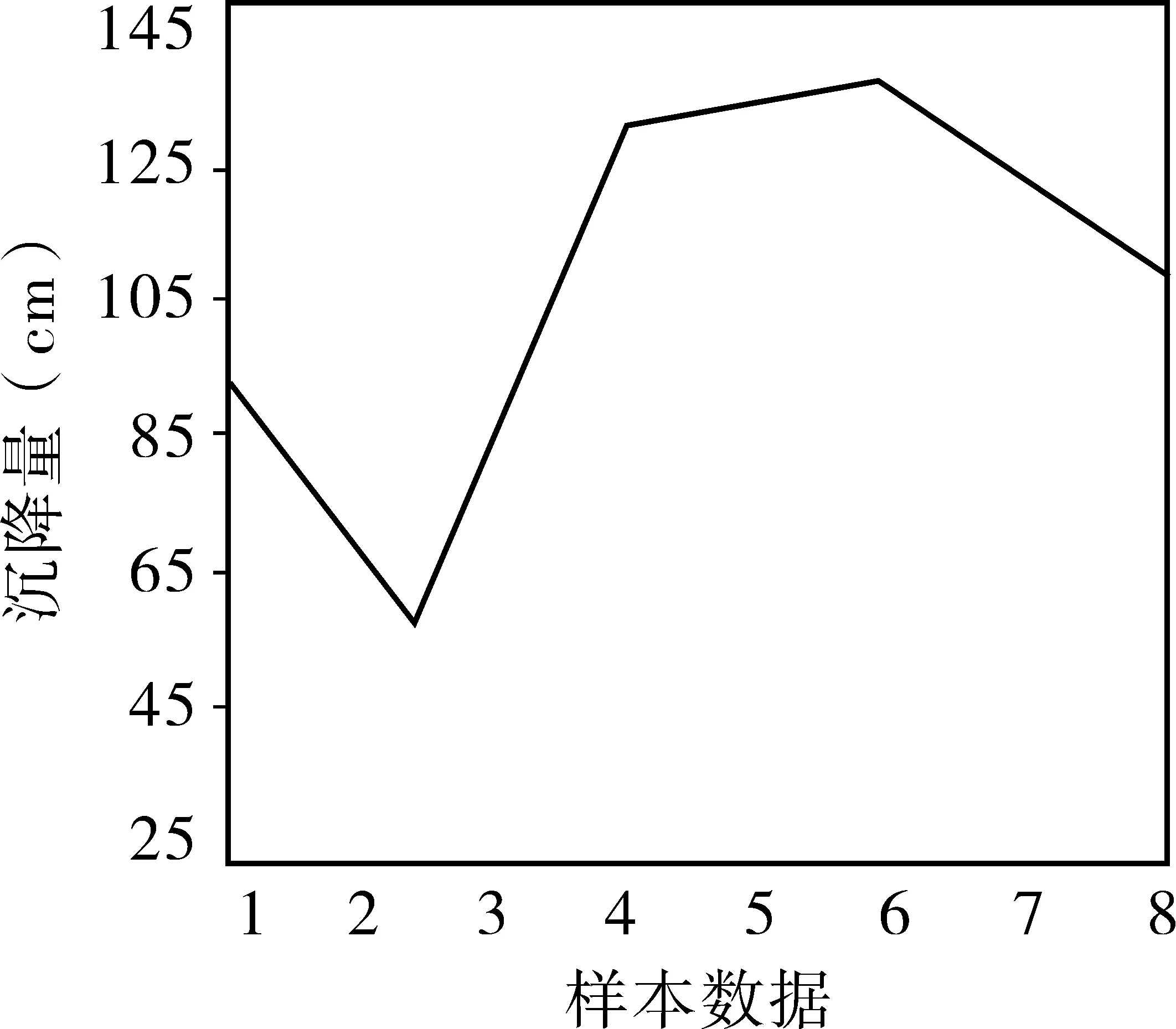
(a)實際測量曲線

通過對圖3數據對比分析發現，采用單一權值變量建立的變權重模型預測結果存在個體系數良好，整體系數異常的問題。因此在經過變權重組合優化后，整體預測值輸出準確性提升明顯，全局系數穩定性良好，預測結果與實際測量結果之間的誤差明顯減小，相較其他權重組合方法預測結果有明顯數據優勢。

3.2 討論

(1)變權重模型預測與其他權重組合模型不同，通過對時間變量對應加權系數的擬合，對應不同時間點下不同樣本點的變化，反映出沉降點的發展趨勢與整體規律。在此種組合過程中，不同沉降數據樣本點擺脫了各種不同約束限制，在整體預測輸出的自適應性與容錯性方面，較其他權重組合預測結果更好。通過本文的變權重組合模型優化后，公路路基沉降預測系數的收斂速度與其對應的權值以及閥值，都得到了相應提升。

(2)基于高速公路路基沉降數據樣本(某高速公路四標段)，利用變權重組合預測模型對高速公路路基的整體沉降數據進行預測，得到較為精準的預測結果，預測結果與實際公路路基沉降測量值之間的誤差系數僅為0.871 2，相較其他權重組合模型預測結果得到的誤差系數更小，數據擬合度更高。

4 結語

針對高速公路沉降問題建立預測模型，是分析路基沉降數據的關鍵。根據高速公路路基地質結構的不同，對應沉降產生原因也有所不同，其中對應的沉降權重系數決定了預測量的精準程度。高精準度的預測模型能夠為災害防控、道路維護提供數據基礎。在保證實際測量條件不變的前提下，通過變權重組合方式建立沉降預測模型，將沉降問題與時間量進行關聯，按照沉降產生的時間順序，實時反映沉降趨勢與規律，最大程度減小預測量與實際測量值之間的誤差。通過與實例中多種權重組合預測模型的對比，證明了變權重組合模型路基預測精準度更好，可為高速公路路基沉降預測提供一種新方法。