地鐵隧道基底飽水風化軟巖動力特性試驗研究

談亦帆,石鈺鋒,徐長節,3,詹剛毅

（1. 江西省建筑設計研究總院集團有限公司，南昌 330013；2. 華東交通大學 江西省巖土工程基礎設施安全與控制重點實驗室，南昌 330013；3. 浙江大學 濱海和城市巖土工程研究中心，杭州 310058；4. 中鐵上海設計院集團有限公司，上海 200070）

隨著地下空間的大量開發利用，城市地鐵已成為現代城市高速發展的產物。然而，地鐵運營期間列車反復荷載作用產生的動力響應會對地鐵的運維造成很大困難。為此，地鐵隧道基底長期變形及預測越來越受到重視，眾多學者對軟土地基在交通荷載作用下的長期沉降研究甚多，而對風化泥質粉砂巖的研究較少。事實上，此類軟巖物理力學性質較差，具有易擊碎、遇水軟化崩解等特點，在長期列車荷載作用下會對隧道結構產生不利影響。因此，研究循環荷載作用下風化泥質粉砂巖的累積變形具有重要工程意義。

列車循環荷載作用下巖(土)體動力變形特性已受到眾多學者的密切關注。Seed等[1]對軟黏土進行循環三軸試驗，研究了循環荷載作用下軟黏土的動力變形規律；Yoshinaka等[2]通過對不同軟巖進行動三軸試驗，研究了軟巖孔隙水壓力和動模量變化規律；Chen等[3]以海洋黏土為對象進行了循環三軸試驗，研究發現，加載頻率越大，黏土的累積應變反而越小。劉飛禹等[4]通過室內動三軸試驗，研究了循環荷載下初始偏移應力、頻率等對軟土動彈性模量衰減的影響，得出頻率對試樣動彈性模量影響較小，初始偏移應力的增加對其動彈型模量影響較大的結論；Tang等[5]對飽和黏土進行循環動三軸試驗，根據累積塑性應變與循環次數的關系曲線特征，提出能夠很好地反映動應變發展的指數型模型；陳成等[6]以泥炭質土為研究對象，開展考慮動應力幅值、靜偏應力等不同因素的不排水動三軸試驗，發現動應力幅值和靜偏應力不僅對其累積塑性應變影響顯著，還會加劇動孔壓的發展；于升才等[7]對飽和黏性土的滯回環形態特征、塑性變形等規律進行了研究，發現隨著循環次數增加,黏性土滯回環由梭形逐漸收縮變成S形，且滯回環高度、寬度逐漸變小，試樣塑性變形大小隨總應變的增大而增大；匡月青[8]對地鐵荷載作用下飽和軟黏土進行動三軸試驗，研究了軟黏土累積塑性應變和動應力—動應變關系特性，并提出了考慮頻率和動應力比的累積應變數學模型；羅文俊等[9]對飽和紅黏土進行循環三軸試驗，研究了動應力比、排水條件等影響因素對紅黏土塑性累積應變和動孔壓的影響，發現隨著動應力比的增大，紅黏土變形曲線由漸穩型向破壞型過渡，不排水條件下的累積應變要大于排水條件下的累積應變；冷伍明等[10]通過大型動三軸試驗，分析粗粒土在圍壓、動應力等影響因素下其累積塑性應變變化規律，結果表明，累積塑性應變及其穩定值隨動應力的增加而增大,隨圍壓的增加而減小；孫靜等[11]研究了多次凍融循環后粉砂土動應力、動模量等動力參數的變化規律；任華平等[12]通過室內動三軸試驗，研究了在飛機荷載作用下荷載頻率和壓實度對粉土道基累積塑性應變的影響，結果表明，壓實度對累積塑性應變及臨界循環應力比均有影響，荷載頻率對加載前期的累積塑性變形發展速率影響較為顯著。

從已有研究可以看出，針對交通荷載作用下巖(土)體材料最主要的研究對象是軟黏土、砂土等，對軟巖的研究較少，對風化軟巖的研究更少且只考慮經過物理改良后作為路基填料的穩定性指標等要求，但水—巖耦合作用下風化軟巖在交通荷載作用下累積變形問題日益突出。筆者以飽水全、中風化泥質粉砂巖為研究對象，分別從動應力幅值、加載頻率等因素條件下開展動三軸試驗，探究全、中風化泥質粉砂巖的主要影響因素和累積變形特性。

1 試驗方法

1.1 試驗設備

試驗采用的儀器設備是英國GDS試驗系統，主要由軸向驅動裝置、圍壓控制器、內壓控制器、反壓控制器、數據采集儀和數據采集系統等主要部分組成。加載方式有正弦波、半正弦波、余弦波等，加載頻率范圍為0～2 Hz；軸向最大加載壓力為10 kN；最大軸向變形為20 mm；應變測量精度為0.000 1；最大圍壓為2 MPa，每個循環周期最多可記錄500個數據點，控制方法有應力控制和應變控制。試驗采用應力控制，巖樣經歷加載—卸載—再加載的過程，在整個過程中，巖樣所承受的塑性應變的累加即為累積塑性應變。

1.2 試驗取樣與制備

試驗共取兩種不同風化程度的軟巖。其中，中風化泥質粉砂巖取自南昌地鐵二號線東延項目某車站現場，采用鉆孔取芯方式取樣，取出來需立即用塑料膜包裹，防止其風干開裂，取樣深度為25～31.5 m。中風化泥質粉砂巖呈暗紅、紫紅色，粉砂質結構，泥質膠結，節理裂隙發育，巖芯以柱狀、長柱狀為主，少量短柱狀，節長一般為5～30 cm，如圖1所示。RQD=80%，采取率95%，錘擊聲悶，屬極軟巖。全風化泥質粉砂巖因風化強烈，巖芯呈半巖半土狀、碎塊狀，鉆孔取芯后無法制備成試驗所需的標準試樣，并且考慮到在盾構施工過程中，盾構機對圍巖擾動很大，因此，全風化泥質粉砂巖采用重塑的制樣方法。巖樣取自地鐵二號線某車站基坑。

圖1 鉆孔取樣圖Fig.1 Drilling sampling

按照《巖石試驗規范》參考引用和《土工試驗規范》參考引用中的規定用磨石機和切割機加工成直徑50 mm，全風化泥質粉砂巖采用分層濕搗法，并控制顆粒級配、最大干密度為1.9 g/cm3和最優含水率為14.5%進行重塑，巖樣的基本物理力學指標見表1，全、中風化標準試樣見圖2。

表1 巖樣的基本物理力學指標Table 1 Basic physical and mechanical indexes of rock samples

圖2 標準試樣Fig. 2 Standard sample

1.3 試驗方案

宮全美等[13]采用不同的正弦加載方式進行室內動三軸試驗，發現用半正弦波加載方式的試驗數據與實測數據更吻合。試驗不考慮列車非勻速狀態下動應力幅值的變化，采用單向等幅半正弦波的加載方式。南昌地鐵列車運行速度為80～100 km/h，列車軸重不大于14 t，根據公式σd=0.26P×(1±0.004V)和ηd=σd/σf(σd、P、V、ηd和σf分別為動應力幅值、列車軸重、運行速度、動應力比和靜極限強度，根據地勘報告資料，全、中風化軟巖靜極限強度分別為0.3、1.5 MPa)得出全、中風化軟巖動應力比，如表2所示。已有研究表明[14]，靜偏應力越大，巖(土)材料達到破壞時所需時間越短，因此，選取0、75、100、150 kPa不同靜偏應力進行試驗(ηs=σs/σf，ηs和σs分別為靜偏應力比和靜偏應力)。圍壓一般根據土體埋深進行計算，即σ3=k0γh，全風化泥質粉砂巖埋深為25～27 m；中風化泥質粉砂巖埋深為27～31.5 m，因此，選取300、450、600 kPa進行試驗。根據前人的研究，通過現場監測得出地鐵列車以不同速度經過時，隧道圍巖會產生低頻（0.4～0.6 Hz）和高頻（2.5～2.8 Hz）兩種頻率。因此，試驗主要加載頻率為1 Hz，且選取0.5、2 Hz兩種工況進行對比分析。

表2 風化泥質粉砂巖試驗工況表Table 2 Test condition table of weathered argillaceous siltstone

試樣放入真空飽和缸中進行預飽和，然后在GDS試驗設備中進行反壓飽和，當檢測值B=Δu/Δσ＞95%時，則認為試樣飽和，最后進行等向排水固結，當超孔隙水壓力消散到等于反壓值時，則認為固結完成，試樣在等壓固結完成后，立即施加靜偏應力和動應力，試樣加載見圖3。

圖3 試樣加載圖Fig. 3 Sample loading diagram

全、中風化軟巖各進行了15組試驗，試驗采用各向等壓固結，即固結應力比為1.0。定義動應力比ηd=σd/σf(σd為動應力幅值，σf為靜極限強度)；定義靜偏應力比ηd=σs/σf(σs為靜偏應力，σf為靜極限強度)，具體工況見表2。

2 試驗結果分析

2.1 動應力比的影響分析

為研究不同動應力比對巖樣累積塑性應變的影響，分別對試驗工況1和工況5進行動三軸試驗。

由圖4（a）、（b）可知，不同動應力比對巖樣的累積塑性應變影響較大。當動應力比分別為0.133、0.167、0.233、0.3時，試樣變形規律呈穩定型，變形規律大致相同；當動應力比為0.4時，試樣變形規律呈破壞型，循環次數達到600次時，試樣變形速率突然增大，其斜率要遠大于加載初期階段，累積塑性應變曲線發展迅猛，最終達到破壞，可知全風化泥質粉砂巖的臨界動應力比為0.3～0.4。另外，穩定型曲線加載前1 000次累積應變占總應變(10 000次)的75%～80%，這是由于全風化軟巖內部結構松散，孔隙數量較多，加載初期巖樣被壓實，累積變形急劇增大。由圖5可知，5種工況均為穩定型曲線，加載前100次累積應變占總應變的85%～95%，相較于全風化軟巖而言，中風化軟巖達到穩定階段所需的循環次數更少且中風化軟巖加載初期應變占總應變比例更大，這是因為中風化軟巖巖芯較完整，內部裂隙數量較少，顆粒之間膠結作用較強，宏觀上表現為抵抗變形能力較強，因此，前幾十次循環次數累積塑性應變曲線就已經趨于平穩。

圖4 不同動應力比下全風化軟巖與加載次數的關系Fig. 4 Relationship between fully weathered soft rock and loading times under different dynamic stress ratios

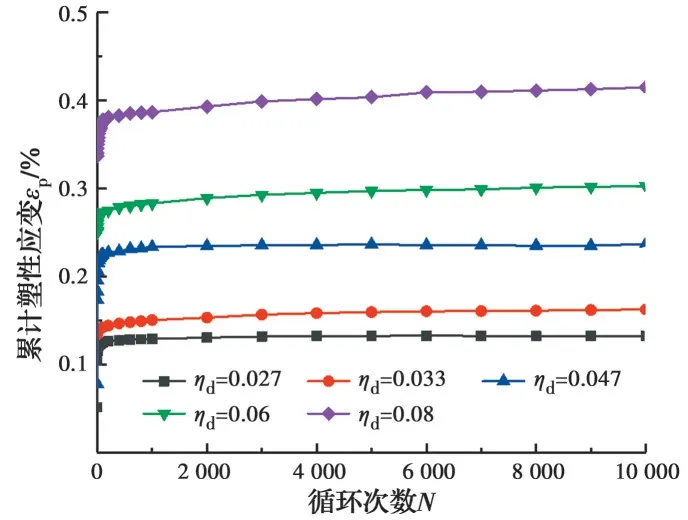
圖5 不同動應力比下中風化軟巖與加載次數的關系Fig. 5 Relationship between moderately weathered soft rock and loading times under different dynamic stress ratios

2.2 靜偏應力比的影響分析

為研究不同靜偏應力比對巖樣累積塑性應變的影響，分別對試驗工況2和工況6進行動三軸試驗。

對于全風化軟巖而言，如圖6所示，當靜偏應力比為0時，巖樣總應變為0.351%，靜偏應力比增大到0.333時，總應變達到0.655%，增幅為86.6%，但累積塑性應變曲線仍為穩定型。當靜偏應力比為0.5時，巖樣總應變高達1.828%，是靜偏應力比為0時的5.2倍，累積塑性應變曲線呈破壞型，巖樣被破壞。可見，當巖樣飽和時，巖樣顆粒之間的結合作用被破壞，導致黏合力損壞甚至被破壞[15]，繼而誘發巖樣內部原生裂隙的發展和次生裂縫的萌發，引起巖樣的損傷，在施加動荷載過程中會加快巖樣變形速率，最終導致破壞。對于中風化軟巖而言，如圖7所示，4種工況下巖樣累積塑性應變曲線均為穩定型。當靜偏應力比從0增大到0.1時，巖樣所對應的總應變從0.101%增加到0.312%，后者是前者的3.1倍。說明靜偏應力對中風化巖樣的影響較全風化巖樣更小，這是由于中風化巖樣結構完整，動強度較大，在循環荷載作用下很難產生較大的變形。

圖6 不同靜偏應力比下全風化軟巖與加載次數的關系Fig. 6 Relationship between fully weathered soft rock and loading times under different static deviator stress ratios

圖7 不同靜偏應力比下中風化軟巖與加載次數的關系Fig. 7 Relationship between moderately weathered soft rock and loading times under different static deviator stress ratios

2.3 圍壓的影響分析

為研究不同圍壓對巖樣累積塑性應變的影響，分別對試驗工況3和工況7進行動三軸試驗。

由圖8可知，不同圍壓下巖樣累積塑性應變曲線均為穩定型。隨著圍壓的增大，全、中風化軟巖累積應變反而越小，其原因是巖樣吸水后，原有的結構特征被完全破壞，重塑過程中巖樣顆粒和孔隙重新排列，導致巖樣裂縫減少[16]，顆粒之間膠結作用增強，巖樣更密實，物理力學指標表現為動強度越大，累積塑性應變越小。相較于不同動應力比和靜偏應力比，改變圍壓對巖樣累積塑性應變影響不大。當圍壓從600 kPa減小到300 kPa時，全風化軟巖的總應變從0.354%增加到0.552%，增幅為56.0%；中風化軟巖的總應變從0.129%增加到0.201%，增幅為55.7%，說明圍壓的改變對不同風化程度軟巖的影響大致相同。

圖8 不同圍壓下風化軟巖與加載次數的關系Fig. 8 Relationship between weathered soft rock and loading times under different confining pressures

2.4 加載頻率的影響分析

為研究不同頻率對巖樣累積塑性應變的影響，分別對試驗工況4和工況8進行動三軸試驗。

由圖9可知，加載頻率越低，全、中風化軟巖的總應變反而越大，其原因是在加載頻率較小的情況下，動荷載作用時間更長，孔壓消散和裂隙發育更快，巖樣累積塑性應變急劇增加。對于全風化軟巖而言，當頻率為0.5 Hz時，加載到10 000次巖樣仍有應變繼續增大的趨勢，由于試驗周期過長，沒有考慮更多循環次數和更低頻率下累積應變的變化規律，后期可考慮增加循環次數和減小頻率的工況；對于中風化軟巖而言，低頻區段內改變頻率對其影響不大，由于試驗設備最大加載頻率為2.0 Hz，因此，高頻區段內改變頻率的影響有待探究。

圖9 不同加載頻率下風化軟巖與加載次數的關系Fig. 9 Relationship between weathered soft rock and loading times under different confining pressures

2.5 孔隙水壓力變化分析

地鐵運營初期，盾構隧道施工擾動引起隧底圍巖的超孔隙水壓力仍未消散，列車長期荷載作用會引起超孔壓減小而導致固結沉降，所以，超孔隙水壓力對地鐵運營期的長期沉降影響需要引起重視。在設定靜偏應力比0.25、圍壓300 kPa、頻率1 Hz的條件下，分析全風化軟巖動應力比分別為0.133、0.167、0.233、0.3、0.4的 超 孔 隙 水 壓 力 的 變 化 規律；在設定靜偏應力比0.05、圍壓450 kPa、頻率1 Hz的條件下，分析動應力比分別為0.027、0.033、0.047、0.06、0.08的孔隙水壓力變化的規律。定義U*為孔壓歸一值，U*=Δμ/σ3，Δμ為超孔隙水壓力，σ3為有效圍壓。

由圖10可知，對于中風化軟巖而言，最大動孔壓為0.293；對于全風化軟巖而言，最大動孔壓為0.42，遠大于中風化軟巖，這是由于全風化軟巖采用重塑制樣方式，其原有內部結構已遭到破壞，顆粒之間膠結作用減弱，在循環荷載作用下，有利于空壓的發展。另外，當全、中風化軟巖從最小動應力比增加到最大動應力比時，動孔壓增幅約為65%，因此，地鐵運營期不僅要關注列車長期荷載作用下的累積變形，還需要著重關注固結沉降。

圖10 不同動應力比下動孔壓比隨循環次數的變化關系Fig. 10 Relationship between dynamic pore pressure ratio and cycle times under different dynamic stress ratios

3 累積軸向塑性應變模型的建立

目前，經驗公式模型主要有對數型[17]和指數型[18]兩大類，未見風化泥質粉砂巖地層的累積塑性應變數學模型。結合風化泥質粉砂巖循環動三軸試驗變化規律和影響因素，本模型采用新累積塑性應變數學模型。

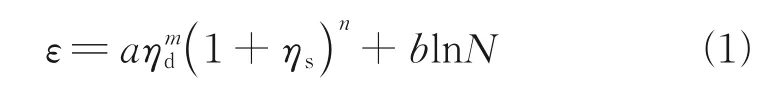
式中：ε為風化泥質粉砂巖累積塑性應變；ηd為動應力比；ηs為靜偏應力比；N為循環次數；a、b、m和n為擬合參數。

通過MATLAB軟件進行編程，采用最小二乘法進行擬合，得出全風化泥質粉砂巖中a、m、n和b分別為0.780 8、2.748 1、12.047 9和0.046 7，R2=0.92，得出中風化泥質粉砂巖中a、m、n和b分別為3.102 2、1.166 1、15.589 1和0.005 6，R2=0.97，兩種風化軟巖擬合結果均較好。圖11、圖12分別為不同動應力比和不同靜偏應力比條件下風化泥質粉砂巖試驗數據和擬合數據的對比。

圖11 全風化泥質粉砂巖試驗數據與擬合數據對比圖Fig. 11 Comparison of experimental data and fitted data of fully weathered argillaceous siltstone

圖12 中風化泥質粉砂巖試驗數據與擬合數據對比圖Fig. 12 Comparison of experimental data and fitted data of moderately weathered argillaceous siltston

4 結論

1）不同動應力比條件下，全風化軟巖在加載1 000次左右開始趨于穩定，其臨界動應力比在0.3～0.4之間，中風化軟巖在加載100次左右開始趨于穩定，并且相較于全風化軟巖，中風化軟巖加載初期的累積應變占總應變的比例更大。

2）動應力比和靜偏應力比越大，兩種風化程度軟巖的累積塑性應變均增大；圍壓和頻率越大，兩種風化軟巖累積總應變均越小，但相較于不同動應力比和靜偏應力比，改變圍壓和頻率對兩種風化軟巖總應變影響不大。

3）隨著動應力比的增大，超孔隙水壓力增大，其趨于穩定所需的時間也越長；相同動應力比情況下，中風化軟巖要遠小于全風化軟巖的超孔隙水壓力。因此，地鐵運營期不僅要關注列車荷載作用下的累積變形，還需要著重關注固結沉降。

4）分析試驗結果數據，提出了考慮加載次數、動應力比等因素的累積塑性應變數學模型，為預測隧道長期沉降提供理論基礎。