橋梁型式對40 m簡支梁磁浮車致動力響應的影響

李小珍,胡啟凱,王渝文,王黨雄

（1. 西南交通大學 土木工程學院，成都 610031；2. 西北工業大學 力學與土木建筑學院，西安 710072）

與傳統的輪軌交通相比，磁浮列車通過電磁力懸浮于軌道上方，不與軌道梁相接觸，具有高速、舒適、便捷、低耗等優點，其應用前景廣闊[1]。中低速磁懸浮列車通過主動懸浮控制產生電磁懸浮力，使磁懸浮列車能夠穩定懸浮并平穩運行，其車橋耦合振動問題涉及磁浮列車、懸浮控制系統和軌道梁3個模塊之間的相互耦合作用[2]。

在磁浮系統的車橋耦合振動方面，已有學者進行相關研究，Deng等[3]提出了高溫超導磁懸浮車—橋耦合系統的6個自由度動力學模型，并模擬了不同條件下的動態響應。Zhao等[4]建立了10個自由度的磁浮列車模型并討論了隨機不規則激勵引起的豎向耦合振動特性。文獻[5-6]探討了懸浮間隙在不同跨度和橋梁剛度下的變化規律。Wang等[7]利用通用機械軟件對高溫超導磁懸浮車—橋耦合系統的動力學性能進行仿真，并對不同速度范圍內的高溫超導磁浮車—橋耦合系統進行了進一步的設計。Han等[8]討論了橋梁質量、剛度和阻尼對磁懸浮列車動力性能的影響。Lee等[9]重點研究了運行速度、軌道不平順、橋跨長度和橋梁阻尼比對懸浮間隙的影響。Milani等[10]基于自適應魯棒控制系統，研究了具有時滯效應、參數不確定性和外部負載的磁懸浮列車運行的穩定性。Zhou等[11]對軌道不平順引起的磁懸浮列車振動進行了調查，提出了一種自適應振動控制方案來降低磁懸浮列車的振動。韓霄翰等[12]研究了軌道梁結構對中低速磁浮車—軌耦合振動的影響。

隨著橋梁建造技術的提高，在靜力技術上，磁浮線路中較大跨度混凝土簡支梁已經日趨成熟，設計者可以設計不同型式的簡支梁來提高其豎向剛度（如箱型梁上梁、并置單線梁等），但其在磁浮列車作用下的動力性能目前未知，且研究較少。筆者在前人研究的基礎上，針對梁軌一體和梁上梁兩種40 m混凝土簡支梁方案，建立精細的磁浮列車—簡支梁系統耦合振動理論模型，深入探討磁浮列車作用下40 m簡支梁的車致動力響應特征，并對不同型式的40 m簡支梁對系統耦合振動的影響機理進行剖析。

1 中低速磁浮列車—橋梁的動力相互作用模型

1.1 中低速磁浮車輛的豎向模型

以LMS中低速磁浮列車為研究對象，主要構件包括車體、二系懸掛、懸浮架等，車體通過二系懸掛與懸浮架連接，每節列車有5對懸浮架，每對懸浮架有4對懸浮電磁鐵，同時，每個懸浮架上有2個二系懸掛與車體相連，圖1為簡化的構造示意圖。

圖1 LMS中低速磁浮列車的簡化示意圖Fig. 1 Simplified diagram of LMS medium-low speed maglev train

實際磁浮列車結構復雜，數值模型不能完全考慮所有部件和連接，因此，對磁浮列車數值模型采用一些必要的假設：數值模型中考慮了主要部件，包括車體、二系懸掛和懸浮框架，除二系懸掛外，這些組件都假定為剛體；將每個懸浮電磁鐵產生的懸浮力簡化為集中力；采用線性彈簧阻尼單元對空氣彈簧進行建模。

車體考慮豎向（zc）、俯仰（βc）2個自由度，每個懸浮架考慮豎向（Zs）、俯仰（βs）2個自由度，因此，每節列車共計12個自由度。根據圖1，作用在車體和懸架上的載荷如圖2所示，其中：Fzij(i=1～5，j=1,2)表示第i個懸浮架上第j個彈簧阻尼力；fsin(i=1～5，n=1～4)表示第i個懸浮架上的第n個懸架力；ds為每個懸浮架上二系懸掛的距離；ls為相鄰電磁力的間距。

根據達朗貝爾原理，磁懸浮車體的豎向和俯仰運動方程為

式中：Mc和Jc分別為車體的質量和俯仰力矩；lxij(i= 1～5, j= 1,2)為車身質心之間的縱向距離。

懸浮架的豎向和俯仰運動方程為

式中：Ms和Js分別為懸浮架的質量和俯仰力矩。

每個彈簧阻尼力可以表示為

式中：Kz和Cz分別為二系懸掛的豎向剛度和阻尼。則車輛的運動方程可寫成

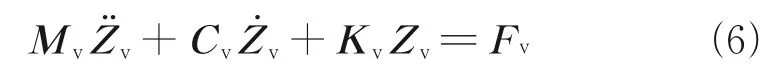
式中：Mv為車輛運動方程的質量矩陣；Cv為阻尼矩陣；Kv為剛度矩陣；Fv為外荷載列向量；Zv為自由度矩陣。

1.2 橋梁系統模型

將軌道結構和橋梁模型視為單個橋梁系統，并使用模態疊加理論[13]進行求解，在外荷載作用下，橋梁的運動微分方程為

式中：m、c、k分別為橋梁的質量矩陣、阻尼矩陣、剛度矩陣；f為作用于橋梁的外荷載（電磁懸浮力）列向量。

利用模態疊加法，橋梁的位移可表示為

式中：φn為橋梁的第n階振型向量；qn為橋梁的第n階廣義坐標。

將式（8）帶入式（7）中，基于振型的正交性，建立橋梁系統模型的解耦微分方程

式中：q?n、q?n、qn為橋梁的n階廣義加速度、速度以及位移坐標；ξn為橋梁的第n階阻尼比；ωn為橋梁的第n階自振頻率；為關于橋梁質量歸一化的橋梁各階振型*

n為經過振型歸一化后的廣義外荷載。在求解橋梁系統運動微分方程時，只需求出系統的固有頻率和作用在橋梁上的廣義外荷載。一般情況下，通過有限元軟件ANSYS對橋梁體系結構離散化，即可得到各種類型的橋梁體系在任意節點處的自振頻率、振型和n階廣義外荷載值。

1.3 PID主動懸浮控制系統模型

中低速磁浮列車通過U形電磁鐵和導軌之間的電磁力支撐車體，如圖3所示。

圖3 電磁鐵懸浮模型Fig. 3 Electromagnet suspension model

由電磁理論[14]可知,電磁懸浮力和懸浮間隙的平方成反比，與線圈電流的平方成正比，其計算公式為

開環的電磁懸浮系統不穩定，即使受到很小的外部干擾都會失去平衡。為了實現穩定懸浮，必須進行主動反饋控制。采用PID主動懸浮控制系統模型，基于位移—速度—加速度反饋的PID主動懸浮控制系統的波動電流Δi(t)可以用懸浮間隙波動值Δc(t)、電 磁 鐵 的 絕 對 速 度Δx??(t)和 絕 對 加 速 度Δx?(t)表示，如式（12）所示。

式中：Kp、Kv、Ka分別為位移、速度以及加速度反饋系數。懸浮間隙波動值為實時懸浮間隙與額定懸浮間隙（8 mm）的差值，然而磁鐵絕對速度信號Δx??(t)一般不能直接測得，需要使用狀態觀測器，借鑒文獻[14]，狀態觀測器的表達式定義為

式中：ξ0、ω0分別為系統狀態觀測器的阻尼和特征頻率，Δc?(t)、Δc??(t)、Δz??(t)、Δz??(t)為在狀態觀測器里重構的狀態觀測變量。

通過拉普拉斯變化求得該系統的傳遞方程為

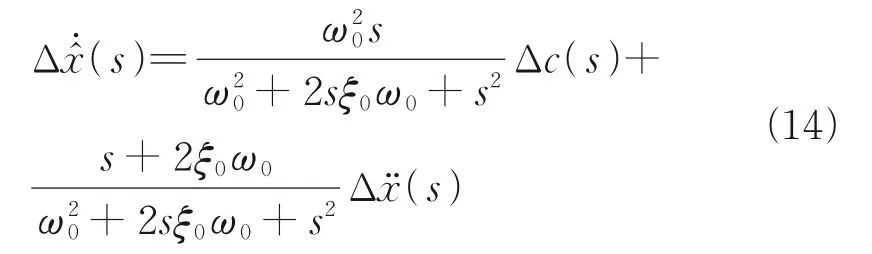
式中：Δx??(s)為狀態觀測器構造的速度反饋變量；s為拉普拉斯變量。

結合式(11)和式(12)可得控制點處的懸浮力為

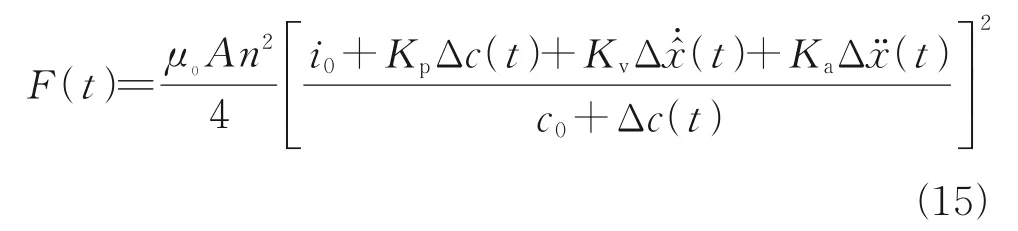
式中：u0為磁導率；i0和c0分別為額定懸浮電流和額定懸浮間隙；A為磁極面積；n為線圈匝數。

通過PID主動懸浮控制，將該懸浮力作用于軌道和磁浮列車的電磁鐵之間，可維持懸浮間隙的穩定，懸浮力與車輛和橋梁的運動狀態密切相關。

1.4 耦合振動模型求解

不同于傳統輪軌，磁懸浮列車在運行過程中沒有輪軌接觸，但軌道不平順會對懸浮間隙造成擾動。為穩定懸浮間隙，電磁鐵與橋梁間的控制器產生電磁力并作用于列車與橋梁，使二者產生振動，加劇了磁浮間隙波動，因此,磁浮列車與橋梁是一個耦合系統。電磁力作為紐帶，將橋梁與車輛的運動聯系在一起，與橋梁及車輛的運動狀態緊密相關，形成磁浮列車—橋梁耦合運動的狀態，如圖4所示。

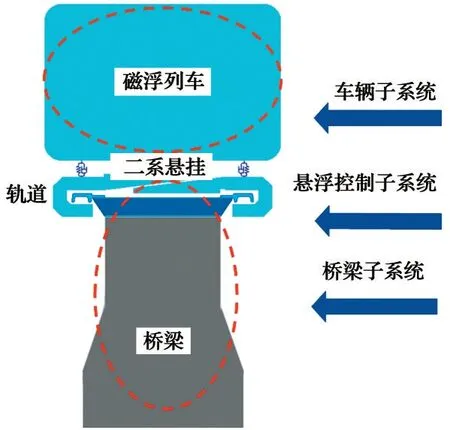
圖4 磁浮列車—橋梁耦合振動系統示意圖Fig. 4 Diagram of maglev train-bridge coupling vibration system

將式（6）和式（9）結合，可得到磁浮列車—橋梁耦合系統的動力相互作用方程

式（16）是一個非線性時變大系統的動力學方程，在求解系統動力學方程過程中，車輛與橋梁系統的等效剛度在車輛運行過程中發生變化，可采用基于Newmark-?積分的分離迭代法求解，將橋梁系統的運動方程與車輛分離，再用Newmark積分法逐步求解，具體可見文獻[15]。

1.5 耦合振動模型的可靠性驗證

基于MATLAB編制磁浮車—橋耦合振動分析程序，聯合有限元軟件ANSYS提供橋梁結構的計算信息。以長沙磁浮試驗中典型的25 m簡支梁作為驗證對象，圖5所示為長沙中低速磁浮列車空載以80 km/h的車速在25 m簡支梁上運行時的仿真與實測曲線對比。

由圖5可以看出，由于未考慮F軌，25 m簡支梁豎向撓度的仿真值剛度較小，撓度較大，但波形相近；簡支梁、車輛和懸浮架的動力響應仿真值與實測值均較吻合，證明了所建立磁浮車—橋耦合振動模型的正確性和仿真分析程序的可靠性。

圖5 實測與仿真對比圖Fig. 5 Comparison diagram of measurement and simulation

2 不同型式40 m簡支梁的車致系統動力響應

2.1 方案

采用梁軌一體方案和梁上梁方案兩種型式的40 m混凝土簡支梁，梁軌一體方案將簡支梁和軌道結合成一體，采用并置箱梁，結構構造簡單，其板件結構尺寸較小，而梁上梁方案將承軌梁置于簡支箱梁之上，采用大箱梁，存在頂板、腹板、翼板和底板等板件，而相比于梁軌一體方案，這些板件尺寸較大，相互間的約束較弱。

2.1.1 梁軌一體方案 簡支梁橋跨度40 m，為并置單線箱梁。梁體采用C50混凝土，跨中截面見圖6。二期恒載為每線22 kN/m。

圖6 梁軌一體方案簡支梁跨中截面（單位：cm）Fig.6 Mid span section of simply supported beam in beam rail integration scheme (Unit: cm)

采用通用大型有限元分析軟件ANSYS建立40 m簡支梁梁軌一體方案動力分析模型，全橋使用板殼單元建模，在簡支梁左側支承處約束所有的平動自由度和繞x軸方向的轉動自由度，在右側支承處約束y軸、z軸方向的平動自由度和繞x軸方向的轉動自由度，如圖7所示。

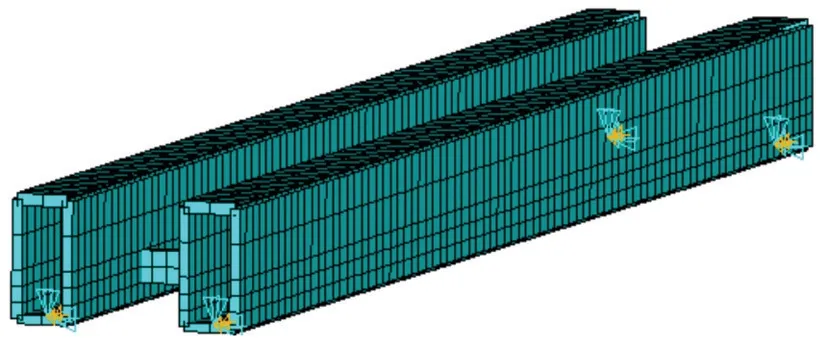
圖7 梁軌一體方案簡支梁ANSYS有限元模型Fig 7 ANSYS finite element model of simply supported beam in beam rail integration scheme

2.1.2 梁上梁方案 梁上梁跨度40 m，為雙線軌道梁。梁體采用C50混凝土，跨中截面見圖8。二期恒載采用每線69 kN/m，其中軌道梁的重量為40 kN/m，實際軌道梁為匹配軌道結構，采用短跨布置，其剛度對箱梁整體剛度貢獻較小，所以將其作為二期恒載加在簡支箱梁上。

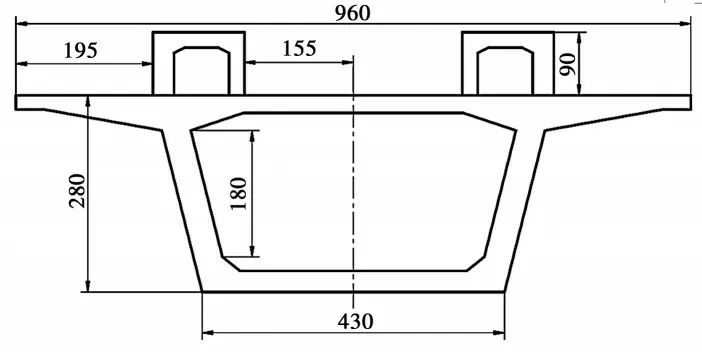
圖8 梁上梁方案簡支梁跨中截面（單位：cm）Fig. 8 Mid span section of simply supported beam in beam on beam scheme (Unit:cm)

同樣地，建立40 m簡支梁梁上梁方案的動力分析模型，全橋也使用板殼單元建模，在簡支梁左側，兩處支承分別約束x軸、y軸、z軸方向和x軸、z軸方向的平動自由度；在右側，兩處支承分別約束y軸、z軸方向和z軸方向的平動自由度，如圖9所示。

圖9 梁上梁方案簡支梁ANSYS有限元模型Fig. 9 ANSYS finite element model of simply supported beam in beam on beam scheme

2.2 模態對比分析

表1分別列出了梁軌一體方案和梁上梁方案下簡支梁的自振特性頻率分析結果，圖10為不同方案中簡支梁典型的模態圖。由表1可知，梁軌一體方案和梁上梁方案的一階正對稱豎彎和一階反對稱豎彎的頻率較為接近，并且梁上梁方案在第15階模態依然發生整體振動，而梁上梁方案在第6階模態就開始出現了局部振動，這是由于梁上梁方案的簡支梁為大箱梁結構，各個板件均較薄弱，根據文獻[16]的研究可知，其較易產生板件的局部振動。

圖10 不同方案典型模態圖Fig. 10 Typical modal diagrams of different schemes

表1 不同方案自振特性對比Table 1 Comparison of natural vibration characteristics of different schemes

2.3 40 m簡支梁的動力響應

在后續分析中，均使中低速磁浮列車在超載的狀態下以最大車速120 km/h通過兩種不同型式的簡支梁，圖11、圖12為兩種型式下簡支梁的跨中豎向最大動撓度和加速度的對比圖。

從圖11可以看出，梁軌一體方案的簡支梁豎向動撓度大于梁上梁方案，最大值分別為5.41、2.75 mm，說明在單線行車的情況下梁上梁方案整體剛度更大。從圖12的時域圖可以看出，梁軌一體方案的橋梁跨中豎向加速度小于梁上梁方案，最大值分別為0.31、0.57 m/s2；從頻域圖可以看出，梁軌一體方案的橋梁振動主要集中在0～5 Hz，主要為低頻振動，優勢頻率為3.01 Hz。除了整體振動外（一階豎彎頻率為3.70 Hz），梁上梁方案還存在明顯的豐富的局部振動模態（主要集中在20～50 Hz），除整體振動外，還表現為高頻振動。結合圖11、圖12可知，梁上梁方案雖然整體剛度較大，但由于在高頻段（20～50 Hz）存在較明顯的局部振動，從而導致豎向加速度在高頻段顯著大于梁軌一體方案。綜合來看，梁上梁方案的振動加速度仍然大于梁軌一體方案。

圖11 簡支梁跨中豎向動撓度對比Fig. 11 Comparison of vertical dynamic deflection of simply supported beams in mid span

圖12 簡支梁跨中豎向加速度對比Fig. 12 Comparison of vertical acceleration of simply supported beams in mid span

2.4 車輛的動力響應

圖13、圖14為兩種簡支梁型式下車體的跨中豎向最大動位移和加速度對比圖。

圖13 車體豎向動位移對比Fig. 13 Comparison of vertical displacement of car body

圖14 車體豎向加速度對比Fig. 14 Comparison of vertical acceleration of car body

從圖13可以看出，梁軌一體方案的車體豎向動位移規律同簡支梁豎向動撓度相似，幾乎為梁上梁方案的2倍，最大值分別為5.17、2.79 mm。從圖14的時域圖可以看出，兩種方案的車體豎向加速度波動規律和數值均相近，最大值分別為0.22、0.20 m/s2；從頻域圖可以看出，兩種方案下車體的振動主要發生在0～15 Hz，梁軌一體方案的優勢頻率為1.09 Hz，梁上梁方案的優勢頻率為7.15 Hz。

2.5 主動控制系統的動力響應

采用基于位移—速度—加速度反饋的PID主動懸浮控制系統來模擬磁浮列車的懸浮控制，圖15為兩種型式下懸浮間隙和懸浮力的對比圖。

圖15 懸浮系統的動力響應對比Fig. 15 Comparison of dynamic response of suspension system

由圖15（a）可知，懸浮系統通過調節電磁懸浮力，使懸浮電磁鐵持續穩定在額定懸浮間隙（8 mm）附近波動，并且波動范圍都較小，單幅波動幅值不超過2 mm，總的波動幅值不超過4 mm。這說明磁浮列車平穩運行時電磁懸浮系統能夠很好地進行主動控制調節，因此，磁浮車體的動位移與橋梁的動撓度數值基本相等。從圖15（b）、（c）可以發現，兩種方案的懸浮力和懸浮間隙的波動規律和數值幾乎相同，并且懸浮力波動值的優勢頻率均為11.14 Hz。

懸浮系統的振動和軌道不平順有關，懸浮系統有自身的優勢頻率，這是固有的屬性，與外界的干擾無關，兩個方案的橋梁型式不同，但軌道不平順相同，結合圖15（c）可知，兩個方案中懸浮系統的優勢頻率相同，其動力響應受橋梁型式影響微弱。

2.6 方案對比

由上述分析可知，和梁軌一體方案相比，梁上梁方案的橋梁剛度更大，變形更小；磁浮列車對低頻振動較為敏感，僅考慮低頻振動時，梁上梁方案的橋梁振動加速度較小，但由于局部振動的影響，總體來看梁軌一體方案的橋梁振動加速度更小；梁軌一體方案是將兩個箱梁用一個個橫隔板連接，其整體性不如梁上梁方案。筆者研究的是40 m簡支梁，在研究更大跨度的簡支梁時，梁上梁方案更優。

由文獻[17]可知，從經濟性角度出發，由于承軌梁不參與結構受力，梁上梁方案材料浪費較多，經濟性較差，而梁軌一體方案梁體體量較小；從施工角度出發，梁上梁方案施工較為復雜，施工精度難以保證，而梁軌一體方案受控因素少，施工更為靈活；從后期維修的角度出發，梁上梁方案維護方便，梁軌一體方案維修較為困難。

綜合橋梁動力響應、經濟性、施工、后期維修等因素，梁軌一體方案更優。

3 不同型式對系統耦合振動影響的機理分析

3.1 簡支梁的波長效應影響

磁浮力對簡支梁結構的激勵頻率的定義如式（14）所示。

式中：v為車輛運行速度，m/s；λ為簡支梁結構振動波長，m；f為周期性不規則引起的激勵頻率，即磁浮力對簡支梁結構的激勵頻率，Hz。磁浮列車的運行速度為120 km/h，激勵頻率和波長的關系如圖16所示，由于梁軌一體方案中簡支梁的頂板和底板寬度較窄，腹板對頂底板的約束較大，所以，梁軌一體方案在低階模態中只有整體振動，局部振動只存在于高階模態，整體振動產生的典型波長為80、40 m（對應表1中的一階正反對稱豎彎）。而梁上梁方案中則存在豐富的局部振動模態，局部振動產生的典型波 長 為40、20、13.33 m（對 應 表1中 的 局 部 振 動模態）。

圖16 簡支梁振動的典型波長Fig. 16 Typical wave length of simply supported beam vibration

軌道不平順特性會影響簡支梁的頻率，磁浮列車對簡支梁的影響是周期性的，當簡支梁變形為規則正弦波時，簡支梁也會產生周期性振動，由于梁上梁方案中存在較多的局部振動，使得簡支梁振動的波長減小。由圖16可知，激勵頻率隨波長的減小而增大，導致梁上梁方案振動加速度幅值更大，所以，簡支梁振動的波長會影響簡支梁本身的頻譜頻率分布特征。

3.2 不同型式的模態影響

由模態對比分析可知，在梁上梁方案中，第6階及之后的模態都出現了局部振動，從而引起的橋梁結構變形中同時存在整體變形和局部變形，文獻[18]指出，中低速磁浮列車中，若考慮F軌的影響，由于其局部振動較為明顯，導致軌道—橋梁系統的位移導納在F軌的局部一階豎彎存在峰值，說明局部振動對橋梁自身變形影響較大，所以，模態的不同會對橋梁變形產生影響；結合圖12的頻域圖可知，由于局部振動發生的頻率較高，和梁軌一體方案相比，梁上梁方案簡支梁的振動主要發生在較高的頻率；結合圖14的頻域圖可知，橋梁的局部振動會反作用于車體。文獻[19]指出，在考慮F軌的局部振動后，車體的豎向振動加速度增大，所以局部振動同時也會影響車體的動力響應，由于局部振動主要存在于高頻中，從而導致梁上梁方案中車體振動的優勢頻率大于梁軌一體方案。

4 結論

建立了考慮主動懸浮控制的中低速磁浮列車—橋梁系統豎向耦合振動模型，針對兩種不同型式的簡支梁，將所建模型進行對比，分析兩種不同方案下40 m簡支梁中低速磁浮車致系統的動力響應，進而探討不同橋梁型式對系統耦合振動的影響機理，得到以下結論：

1）相較于梁上梁方案，梁軌一體方案的橋梁豎向動撓度更大，加速度更小，橋梁振動的優勢頻率分別為3.01、3.70 Hz；梁軌一體方案的車體豎向動撓度大于梁上梁方案，兩種方案的車體豎向加速度相近，車體振動的優勢頻率分別為1.09、7.15 Hz；綜合橋梁動力響應、經濟性等因素，梁軌一體方案更優。

2）懸浮系統有自身的優勢頻率，其動力響應與外界干擾無關，受橋梁型式影響微弱，本文中懸浮系統的優勢頻率為11.14 Hz。

3）梁上梁方案中簡支梁存在豐富的高頻局部振動模態，故存在較密集的短波振動效應，增大了橋梁變形和橋梁與車體的振動優勢頻率。

4）由于橋梁型式不同，簡支梁變形的波長和模態不同，從而通過波長效應、局部振動等影響磁浮列車—軌道—橋梁系統的耦合振動。