車銑復合加工中心動態特性分析

王增，王德倫

（大連理工大學機械工程學院，遼寧大連 116024）

0 引言

制造業是國民經濟的基礎產業，數控機床是國家裝備制造業的基礎裝備和重要代表，加快國家經濟高質量發展和提高綜合國力的重要基石是持續推動高端數控加工技術不斷向前。由于國防軍事裝備、交通運輸載具和信息技術等領域的不斷發展，數控機床的發展趨勢主要集中體現在高生產效率、高加工精度、高可靠性等[1]。

相對而言，機床的加工精度和加工效率與機床本身的靜動態特性相關。本文僅針對機床動態特性進行分析，關于機床靜態特性分析在此不再贅述。對于機床動態特性分析，可以利用動力學分析中基礎的模態分析和諧響應分析得到機床支承件和整機的固有頻率和振型情況[2]。進行動力學分析時，不僅包括機床的主要支承件，而且對于整機的計算也是必須的。進行支承件模態計算時，根據計算得到的固有頻率，機床的一階固有頻率越大，越會遠離機床切削轉速；相對而言，一階固有頻率越小，越容易落入機床切削轉速區，從而使機床產生共振。而機床的整機動力學分析不同于機床整機的靜力學分析，整機動力學分析時必須考慮機床結合面的剛度、阻尼等動力學特性參數，如果只是簡單地與靜力學分析一樣將部件裝配起來就直接分析，就會使得到的分析結果與實際結果之間產生較大的偏差，從而失去參考意義。

當前，隨著計算機技術和有限元技術的迅速發展，有限元方法作為理論建模的重要工具，廣泛應用于各種結構的動力學建模中。Yigit等[3]明確了機床特定頻率內的動態順應性在動態特性分析時尤為重要。Chen Tsung-Chia等[4]利用ANSYS對比分析了不同材料下立柱和主軸箱的靜動態特性。在動態特性方面，與國外相比，國內研究起步較晚，但從國家實施機床重大專項以來發展迅猛，上海交通大學的萬瑩[5]研究了超精密磨床的動態特性和部件間結合面的問題。劉成穎等[6]利用有限元方法分析了臥式加工中心的動態特性。

綜上所述，有限元法在機床的動態特性分析中取得了不菲的成果。但現有文獻對車銑復合加工中心這類機床研究較少，且并未對結合面等效原理和方法進行詳細闡述，本文以DTM-B70車銑復合加工中心為研究對象，使用有限元方法對其動態特性進行深入研究。

1 關鍵零部件動態特性結合面等效原理

將結合面等效為并聯彈簧阻尼系統，在簡諧激振的作用下其動力學方程可寫為

式中：Kn和Cn分別為結合面的動態剛度矩陣和阻尼系數矩陣；xn和x˙n分別為系統各節點位移矩陣和速度矩陣；fn為系統外界激勵載荷。

上述方程的瞬態形式可以寫成以下形式：

則有：

由以上公式可知，結合面的動態剛度與法向面壓、激振源頻率及單位接觸面的振幅有關，并且存在非線性的特點，需要通過實驗確定其各項參數。在DTM-B70車銑復合加工中心的整機動態特性計算中，線軌連接面的參數對整機動態特性的參數影響較大。在缺乏動剛度及阻尼等參數的情況下采用下文中的線軌等效模型，利用彈簧阻尼單元進行等效，在模型中認為3個坐標方向的力矩用6個滑塊的力進行平衡，故單個滑塊不承受轉矩作用，則運動微分方程組為：

2 等效模型的建立

以車銑復合加工中心為研究對象，其主要支承部件的三維模型如圖1所示，建立其有限元模型時，對支承件結合面進行了等效簡化。

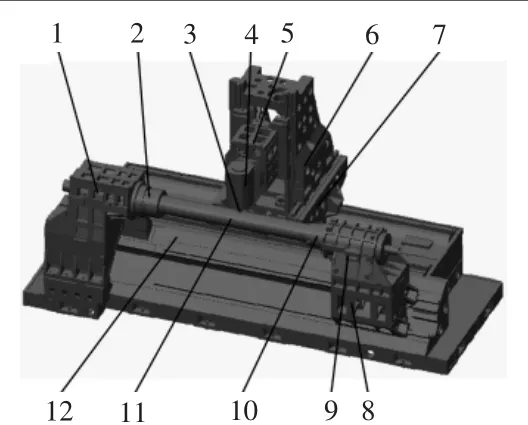
圖1 DTM-B70車銑復合加工中心三維模型

2.1 導軌-滑塊等效

DTM-B70車銑復合加工中心的滑枕-立柱、立柱-床鞍、床鞍-床身、副主軸箱臺架-床身之間為線軌連接，從線軌的結構形式可以看出，線軌連接的剛度主要受導軌與滑塊之間的連接層影響，在模型簡化中，以單個滑塊連接處作為1個子結構單元，對其進行等效。每個滑塊結構中正向、側向均有4個彈簧單元，其關系為并聯，每個滑塊等效為4個正向彈簧單元及4個側向的彈簧單元，如圖2所示。

圖2 線軌結合面有限元計算等效模型

該機床中滑枕-立柱之間的線軌型號為RUE45-EHL-OE-W3-G1-V3，立柱-床鞍、床鞍-床身、副主軸箱臺架-床身之間的線軌型號為RUE55-E-HL-OE-W3-G1-V3，查線軌樣本手冊得其剛度如表1所示。

表1 線軌等效剛度N/μm

2.2 絲杠-螺母等效

DTM-B70車銑復合加工中心的滑枕與立柱、立柱與床鞍、床鞍與床身、副主軸箱臺架與床身之間均為絲杠連接，絲杠在工作時以承載軸向力為主。本文將絲杠軸向等效為沿軸線方向的2根彈簧，將移動件絲杠螺母安裝座及與基礎件絲杠軸承安裝座連接在一起，絲杠和左右軸承座、中間螺母相連，可以看作是2個彈簧的并聯[7]。

根據圖3可列出如下方程：

圖3 絲杠彈簧并聯示意圖

由式（5）可得

式中：F為系統總拉力；F1和F2為單個彈簧拉力；k為絲杠剛度；k1和k2為單個彈簧的剛度；δ為彈簧變形量。

圖4 螺母-絲杠簡化模型

在有限元計算過程中，將螺母和軸承座內圓柱面節點耦合到中心點上。絲杠等效剛度如表2所示。

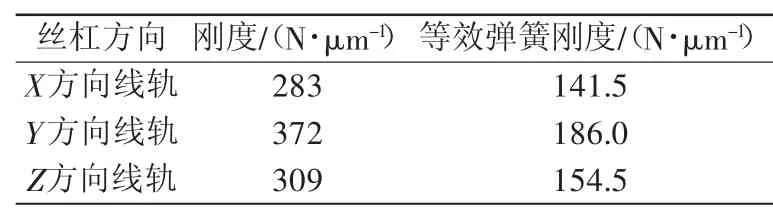
表2 絲杠等效剛度

3 支承件及整機動態性能分析

3.1 支承件模態分析

為了研究機床的固有頻率，使得支承件遠離機床切削轉速，避免機床共振，需對支承件進行模態分析。動力學分析的基礎是模態分析，針對計算結果，設計者可以掌握機床支承件和整機的固有頻率，結合機床實際加工工況，為機床使用提供建議。

進行動態特性計算時，采用第2節所述約束形式進行位移約束，求解該約束狀態下的模態結果，由于本文篇幅有限，僅給出主要部件的網格和前10階模態計算結果。

表3 支承件網格劃分結果

表4 支承件模態分析計算結果Hz

3.2 整機模態分析

基于支承件模態分析，對整機模態進行分析，獲取整機的固有頻率和振型。整機有限元物理模型包括網格劃分和約束模型，如圖5所示。

圖5 DTM-B70整機物理模型

進行求解計算后得到整機前6階模態的固有頻率和振型，如表5和圖6所示。有限元模型中X、Y和Z向分別對應機床坐標系的Z、X和Y向。

圖6 DTM-B70整機模態振型

表5 整機前6階固有頻率和振型

3.3 整機諧響應分析

諧響應分析是指外界激勵作用下，系統各部分的位移響應。根據諧響應分析結果，可以掌握在切削激振力作用下機床整機的抗振性能，從而進一步確定機床薄弱部件。

在該工況下，銑軸銑刀部位的X、Y、Z方向的簡諧力分別設定為1750、2625、4500 N，銑刀對應的工件位置處3個方向的外力分別為-1750、-2625、-4500 N，該簡諧力為極限工況下，依據切削參數計算，得到切削力。根據模態仿真分析得到整機的固有頻率值，將簡諧力頻率范圍設置為0～200 Hz，通過仿真分析得到整機銑刀和工件處在X、Y和Z方向的幅頻響應特性，如圖7所示。

圖7 諧響應分析結果

在銑軸銑刀處，X、Y、Z方向的響應幅值不同，3方向幅值在30 Hz位置附近處于高點，該位置與整機的基頻位置相對應，故機床動態性能主要取決于低階固有頻率，加上根據支承件模態分析結果，可以辨識低階固有頻率對應的主振型是立柱。在工件處，最大幅值出現100 Hz附近，對應整機第8階固有頻率，處于高階固有頻率。

4 結論

根據關鍵零部件動態特性結合面等效原理，介紹了支承件的結合面等效方法，基于支承件結構建立整機的有限元物理模型，分析其動態性能。在動態性能分析中，對關鍵零部件和整機模態分析，得到關鍵零部件的前10階固有頻率和整機的前6階固有頻率和振型，其中立柱的1階固有頻率最低，為78.1 Hz，可知立柱很容易落入機床切削轉速內，從而產生共振；整機由于立柱、床鞍和副主軸箱臺架固定方式的影響，1階固有頻率為29.948 Hz。通過諧響應分析得到，低階固有頻率對機床動態性能的影響較大，且主要是立柱的振型處于低階固有頻率內。故根據動態特性分析，機床立柱為該機床薄弱環節，后續需對立柱進行拓撲優化和參數優化。