一種康復訓練機器人的機構位置逆解

周 燁

(常州劉國鈞高等職業技術學校，江蘇 常州 213000)

據統計，我國有超過1 000萬腦卒中患者，這些患者中幸存下來的大約有75%的患者留下諸多后遺癥，如偏癱、肢體無法正常運動等，其后遺癥嚴重的則會導致生活不能自理[1]。在對后遺癥進行治療和護理的過程中，需對患者進行康復訓練。患者的康復訓練大多依賴基礎醫療器械，隨著機器人在康復醫學中的應用且效果顯著，其應用越來越廣泛，且種類也越來越多[2-3]。

在對康復機器人機構進行設計時，通常有2種方式：一種是已知患者的身體條件并將其轉化為機器人機構的輸入進行正向求解，得出機構的康復訓練執行結果，這種方式也稱為機構的正解；另一種是將患者期望的康復訓練結果作為輸入，對機構進行反向求解，獲得機構的輸入函數，這種也稱為機構的逆解。本文對某一康復機器人機構展開研究，對其機構進行逆解計算。

1 肩關節構型選擇

人體上肢關節分為肩關節、肘關節和腕關節。肩關節是人體上肢關節中最為重要的球窩關節，本文選擇對肩關節康復訓練展開研究。牽引式康復訓練機器人機構可通過牽引人體上肢末端(手部)進行康復運動，完成人體肩關節的運動，從而實現人體上肢肩關節的康復訓練。在機構設計上并聯機構在運動學上具有諸多優點：在運動過程中慣性低、剛度大且負載能力強等，因此成為康復訓練機器人機構設計的首選。并聯機構由靜、動平臺以及運動支鏈組成，綜合考慮人體肩關節的運動性能，同時根據前人的分析可知，3-RRS(為球面并聯機構的簡稱)可實現動平臺上下運動，故將3-RRS球面并聯機構作為實現肩關節構型。

當前學者在機構逆解的算法方面做過較多研究，肖帆在其畢業論文中對復雜多關節工業機器人逆解算法進行了分析和綜述，并對唯一域求逆運動學的方法進行了研究和計算[4]；同濟大學的曾氫菲等對一種多臂協同焊接機器人的運動學進行了逆解，采用的計算方法是基于BP和RBF神經網絡方法，其計算結果表明該方法計算精度較高[5]。本文在綜合前人的研究基礎上結合其研究對象的機構特點，采用矩陣法和閉環矢量法相結合的方法對其進行分析計算，以期獲得機構的逆解。

2 3-RRS肩關節康復訓練機器人機構的運動分析

需進行康復訓練的患者，按日常生活常識當手臂水平位置或者低于水平位置時會由于手臂自身重力而自動下垂，此狀態的機構康復訓練研究不具有實際意義。因此本文以上肢處于水平位置為零度基本位置，以前屈角度為正向角度展開研究，此狀態下上肢手臂的研究最大角度范圍為0°～90°。

將人體上肢簡化為3-RRS機構中的桿件，同時將3-RRS傾斜一定角度就能夠實現肩關節的康復訓練，這也是采用3-RRS機構分析的優點[6-8]。將上肢手臂總長用e表示，并假設康復訓練的患者手臂運動為直線運動，則其掌心(機構終點)的運動軌跡為一弧形，為此掌心的運動起始點、運動終點、肩關節(機構起點)這三者的連線構成一個等腰三角形(見圖1)，其中，e為上肢總長。

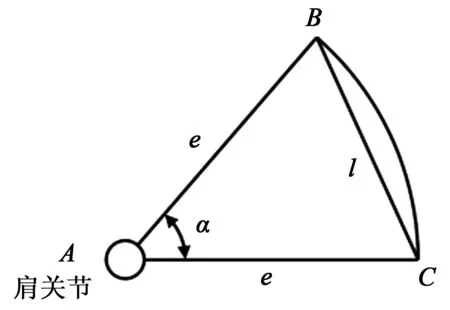
圖1 肩關節運動曲線

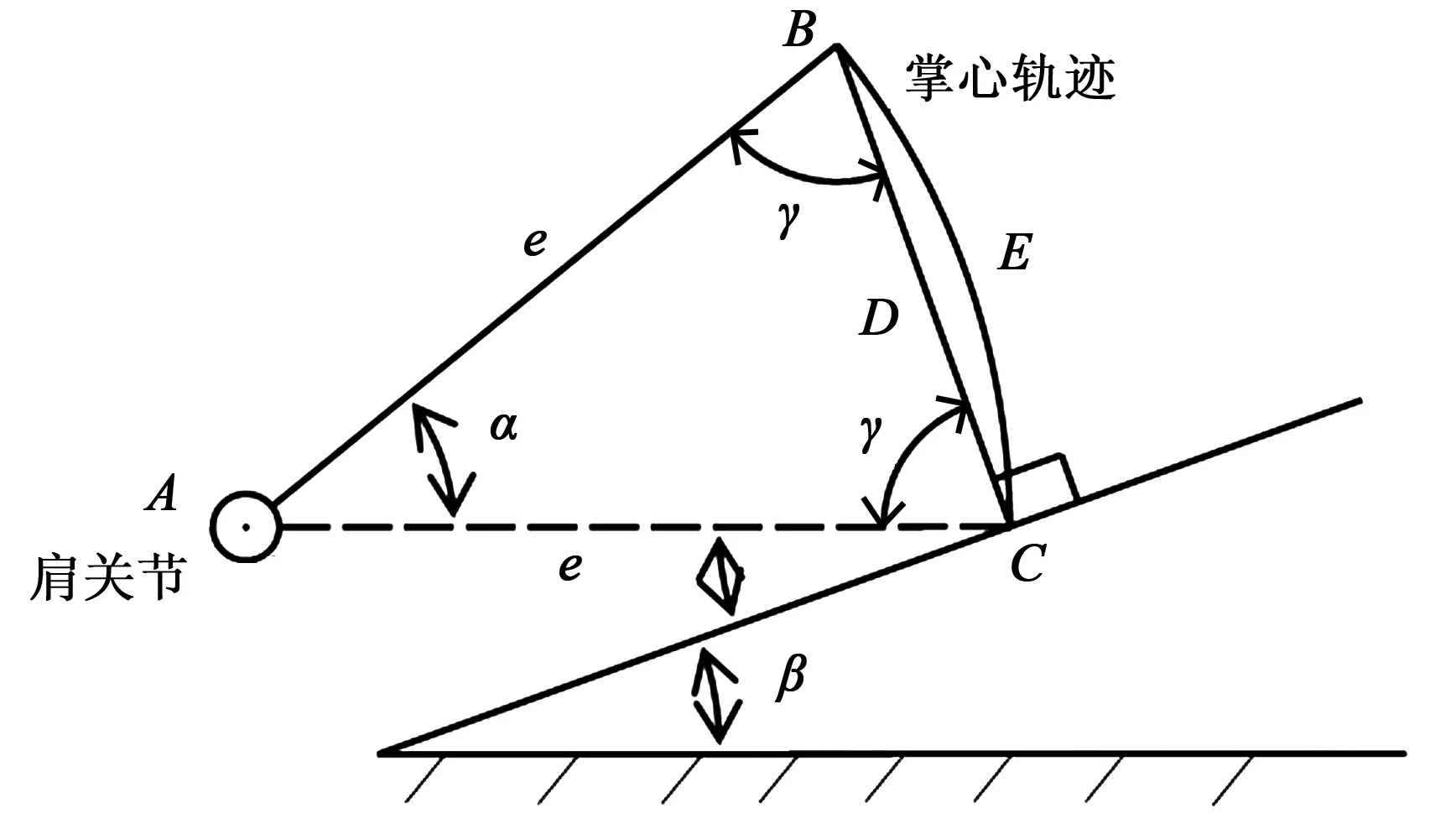
圖2 肩關節運動簡圖

(1)

進一步構建3-RRS機構的運動示意圖如圖3所示，用a表示機構的3條支鏈中的下支鏈長度，用b表示機構的3條支鏈中的上支鏈長度。則在圖3中，根據機構的幾何關系，不難看出存在這樣的關系：角度ψ的取值范圍為0°～180°，即0°≤ψ≤180°。這樣就可以得出桿件l的取值范圍：當ψ=180°時，lmax=a+b；當ψ=0°時，lmin=|a-b|。

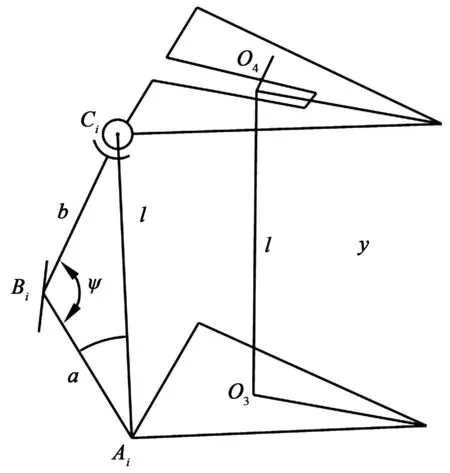
圖3 3-RRS機構運動示意圖

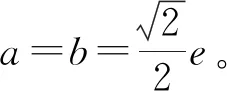
3 康復機器人肩關節機構的位置逆解

將整個求解過程轉化到上述機構中，則并聯機構位置逆解指的是：已知并聯機構運動平臺的位置參數，求解與靜平臺連接的輸入部件的基本條件。本文采用矩陣法和閉環矢量法相結合的方法對3-RRS機構進行位置逆解。

設3-RRS兩個平臺的幾何中心到各端點的距離分別為lO4Ci=r，lO3Ai=R(i=1，2，3)。那么在系統坐標系OXYZ下完成3-RRS并聯機構位置逆解的分析，可根據預知的康復訓練結果反過來求解3個支鏈的具體輸入函數[9-10]。

設底座固定坐標系為O2X2Y2Z2，靜平臺坐標系為O3X3Y3Z3，根據3-RRS機構的應用條件，靜平臺坐標系O3X3Y3Z3繞底座固定坐標系O2X2Y2Z2中X軸旋轉θ角，則坐標變化矩陣T1可表示為：

(2)

矩陣T1表示由底座固定坐標系O2X2Y2Z2向靜平臺坐標系O3X3Y3Z3轉換的坐標變化矩陣。在靜平臺坐標系O3X3Y3Z3中，Ai(i=1，2，3)點的坐標為：

(3)

則Ai在固定坐標系O2X2Y2Z2中的坐標Ai(底)可用下式求解：

Ai(底)=T1·Ai

(4)

以經典的ZYZ型歐拉角(α，β，γ)表示動平臺姿態，c表示cos，s表示sin(下同)。

(5)

用ci、Ci和CO2i分別表示動平臺上球副中心點Ci(i=1，2，3)在局部動坐標系O4X4Y4Z4、靜平臺坐標系O3X3Y3Z3和固定底座坐標系O2X2Y2Z2中的位置矢量。CO4、CO3和CO2分別表示動平臺球副中心點Ci(i=1，2，3)在局部動坐標系O4X4Y4Z4、靜平臺坐標系O3X3Y3Z3和底座固定坐標系O2X2Y2Z2中的齊次坐標矩陣。則有：CO3=T2·CO4，CO2=T1·T2·CO4。

在動平臺坐標系O4X4Y4Z4下，ci點坐標為：

(6)

將式6帶入CO2=T1·T2·CO4中可得：

(7)

因為鉸鏈中心Ai、Bi均為轉動副，所以Ci只能和Ai、Bi在同一個平面內移動，由此列出約束方程如下：

(8)

聯立式7和式8，消除中間變量CiO4(i=1，2，3)的坐標參量，可獲得OO4O3的坐標參量關系方程式：

(9)

為求解動平臺中心O4在底座固定坐標系O2X2Y2Z2中的位置參數，由靜坐標系與底座固定坐標系的變換矩陣T1和O4在靜坐標系O3X3Y3Z3中的位置坐標(XO4O3，YO4O3，ZO4O3)，可得O4在底座固定坐標系O2X2Y2Z2中的位姿參數。

OO4O2i和OO4O3i分別為動平臺中心O4在底座固定坐標系O2X2Y2Z2和靜坐標系O3X3Y3Z3的位置矢量，OO4O2和OO4O3分別為動平臺中心O4在底座固定坐標系O2X2Y2Z2和靜坐標系O3X3Y3Z3的坐標矩陣，則有：OO4O2=T1·OO4O3，同時計算可得：

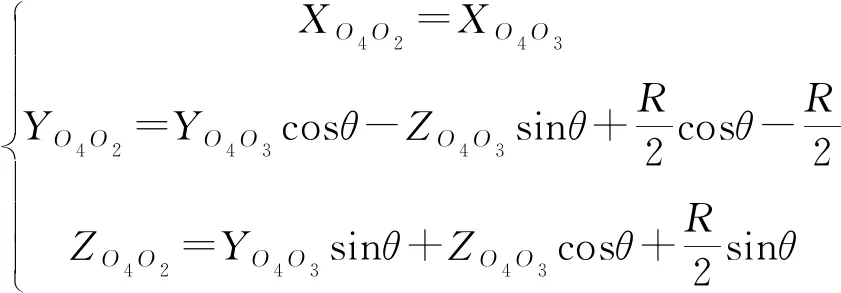
(10)

(11)

由此推出動平臺中心位置的位姿，且得出其位置坐標與靜平臺轉動角度θ之間的關系。

由式5可知，該機構6個姿態參量選取其中任意3個(必須包含ZO4O3)即可確定該機構姿態，在此處取ZO4O3、α、γ為已知參量，則動平臺姿態確定。

根據空間矢量關系，鉸鏈AiCi長度矢量LAiCi可表示為：LO3Ci=LO3Ai+LAiCi，LAiCi=LAiO3+LO3O4-LCiO4。其中，LO3Ci表示O3到Ci的矢量，LO3Ai表示O3到Ai的矢量，LAiCi表示Ai到Ci的矢量，LO3O4表示O3到O4的矢量，LCiO4表示Ci到O4的矢量。

由此，該機構位置逆解即已知ZO4O3、α、γ這3個參量，求解各個支鏈與靜平臺夾角θi1，以及兩支鏈間夾角ψ。

已知動平臺中心的位置坐標和變換矩陣，易得動平臺各個中心點的位置坐標。在三角形AiBiCi中，根據余弦定理，可建立兩支鏈間夾角方程：

(12)

式中，θi1為構件AiBi與靜平臺的夾角；L1i為構件AiBi的長度；L2i為構件BiCi的長度；Li為構件AiCi的長度。求解式12，便可得θi的值。

上述求解便求得了康復訓練機器人機構的桿長、夾角。

4 結語

本文對肩關節康復訓練機器人機構在抽象簡化后進行了運動分析，利用機構的幾何關系和運動關系采用矩陣法和閉環矢量法相結合的方法詳細推導了機構的位置逆解，獲得了康復患者在期望的康復訓練結果下機構3個支鏈的具體輸入函數，即將期望的康復訓練執行動作作為已知條件對機構進行了反向設計，求取了機構的桿長、夾角等參數，其求解結果及分析過程能夠縮短機器人的設計開發周期，且通過計算可以準確地獲得機器人機構桿件的長度，進而為機器人的生產制造提供很好的生產指導，結果具有一定的工程實際應用價值和參考意義。