圖與拓撲關系在建筑生成方法中的應用綜述

李嘉偉 （南京大學建筑與城市規劃學院，江蘇 南京 210093）

1 背景

在計算機輔助建筑設計的研究中，用計算機來進行生成式的設計是比較熱門的話題。基于生成式的設計方法，建筑師可以借助計算機，通過間接的修改設計策略而非直接的修改設計結果的方式，快速大量地獲得建筑設計方案，實現對多種方案的尋優和比較。生成設計工具作為建筑生成設計方法的外在表現，能夠反映生成設計方法的邏輯、操作和結果，也是研究中最重要的部分。生成設計工具通過算法手段，為一類建筑設計問題提供一套固定的求解方法，成為有力的設計輔助工具，助力建筑師在方案設計前期進行方案的快速推敲與篩選，提高設計階段的質量和效率，有效降低設計階段的成本。

圖（Graph）是數學中圖論領域的主要研究對象。圖是由若干給定的頂點及連接兩頂點的邊所構成的圖形，這種圖形通常用來描述某些事物之間的某種特定關系。頂點用于代表事物，連接兩頂點的邊則用于表示兩個事物間具有這種關系。

拓撲關系常被建筑師用作表示建筑設計中各個元素之間的關系。例如，功能拓撲關系圖被用來描述建筑內部功能單元的連接關系。拓撲關系常常以圖作為可視化的載體，我們可以通過圖來研究建筑設計中的拓撲關系問題，進而從這一角度歸納總結形成相關的建筑生成方法。

2 圖與拓撲關系在建筑生成方法中的應用

圖（Graph）源自于圖論，圖論中的圖（G）是由若干給定的節點（V）及連接兩點的邊（E）所構成的一個二元組G=〈V，E〉。可以用圖結構來存儲和使用圖，如圖1。圖結構是一種計算機算法設計中的常用數據結構。它與其他計算機編程中的數據結構（Data Structure）一樣（如鏈表、堆棧、樹結構等），是按照某種順序，對一堆基本數據的封裝方式。

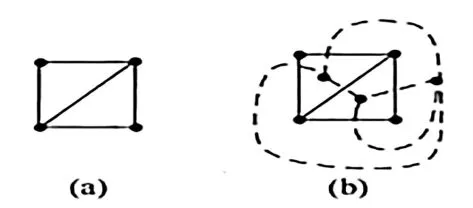
圖1 圖結構與對偶圖（圖片來源：作者自繪）

對偶圖（Dual Graph）是一類特殊的圖，如圖1。它的生成方法是：對于給定平面圖G=〈V，E〉，設G的面為F?，F?，…，F?，當圖G*滿足如下條件時，則圖G*=〈V*,E*〉稱為G的對偶圖。

①對G的每個面F?，內部任選一點v*?∈V*；

②對F?，F?的每一條公共邊界e?，v?*與v?*間有一條邊e?*，并且e?*與e?交于一點；

③當且僅當e?僅是一個面F?的邊界時，v?*有一個環（自回路），e?*與e?相交。

在建筑設計領域中最早開始圖相關的研究是1964年Levin[1]指出了建筑平面布局與圖論兩者之間的關聯。自此之后相關研究逐漸豐富起來。Roth[2]在1988總結了相關研究，將相關研究分類為將圖結構視為關系圖，以及將圖結構視為關系圖的對偶圖這兩個不同的視角。

在建筑設計中，設計師也經常運用泡泡圖來表示建筑各部分之間的關系，可以用圖論中的節點和邊來進行表示，這種類型的圖是屬于將圖結構視為關系圖的視角。在圖結構視為關系圖的視角中，圖結構中的頂點是被視為房間，區域或者是實體，而圖結構中的邊則被視為是房間，區域或者是實體之間的連接關系。

建筑師所常用的平面圖，在簡化掉標注等信息后，也可以在抽象層面上把它視為是一個圖結構。此時這種類型的圖是屬于將圖結構視為關系圖的對偶圖的視角。作為對偶圖，平面圖上墻體或邊界之間的交點被視為是圖結構中的頂點，墻體或邊界則被視為是圖結構中的邊。這個對偶圖所對應的關系圖，就是各個房間或者區域之間的拓撲關系。

基于圖結構進行建筑生成設計的路徑，可以具體分為兩個階段，拓撲階段和幾何階段。在拓撲階段中，主要包括圖結構的整理、復雜圖結構的拆解以及圖結構的二維平面展開這三方面；在幾何階段中，主要是對于抽象圖結構的幾何信息賦予。

2.1 從關系圖視角出發的研究

從關系圖出發的視角，在研究過程中，主要是以圖結構中的節點作為切入，主要需要處理的問題是在幾何階段中，如何在維持現有拓撲關系的情況下，合理的布置節點所代表的房間或區域，同時維持房間或區域的面積屬性。

從關系圖的視角出發的相關研究，思路和方法同質化比較嚴重，基本不會運用圖論相關知識與算法，從關系圖的視角出發的相關研究關注點大多在于對力導向法及其變體形態的發展和優化。

首先是Ruch[3]在1978年，將圖結構中節點的面積作為權值，形成了面積加權的連接圖，并利用這個連接圖，將之轉化為正方形的布局，如圖2所示。這成為了后續從關系圖的視角出發的相關研究的思維起點。

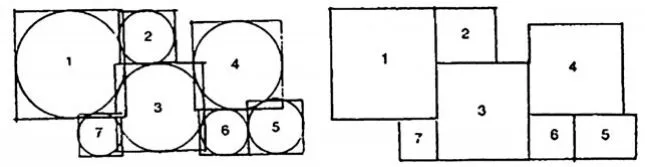
圖2 由關系圖到正方形布局（圖片來源：RUCH J，1978）

Nourian[4]等人參考了 Mitchell[5]的做法，將包含東南西北方位的邊界節點融入原有的只包含房間或區域節點的圖結構的計算，從而得以更好的控制生成結果的朝向。他還使用圖論中的Tutte嵌入（TutteEmbeding）算法[6]，實現了快速將隨意繪制的平面圖進行二維展開，還使用三角剖分的方式窮盡了所有在輸入時沒有明確定義的拓撲連接，拓展探索了隱藏的拓撲解空間。最后基于力導向的結果，如圖3，對圖結構中代表房間的頂點的布置，隨后用Voronoi圖形的原理將房間填滿整個邊界并做了正交規整化的處理，如圖4。Nourian的工作整理和完善整個從關系圖視角的生成方法，并且基于他的工作，開發了Grass?hopper平臺下的SYNTACTIC插件。

圖3 運用力導向法求解功能區的布局（圖片來源：NOURIAN P，2016）

圖4 引入邊界節點的SYNTACTIC插件計算流程（圖片來源：NOURIAN P，2016）

由于圖結構模型數據結構較為復雜，每個頂點與邊之間相關的關聯關系較難以控制，導致在構建、使用和修改圖結構模型時較為繁瑣，郭梓峰[7]基于圖結構與連接矩陣在數據結構上可以相互轉換，選擇使用連接矩陣來構建和修改圖結構，提高了計算效率。郭梓峰也將基于多智能體的圖結構生成方法與格網模型做了結合，從而得到了較為規整化的生成結果。基于三維格網，做了三維空間拓撲關系生成的嘗試。并將生成結果轉化為基于格網的模型，如圖5。

圖5 三維空間拓撲關系生成及形體轉化（圖片來源：郭梓峰，2017）

Egor[8]等人提出的Magneitizing算法，并基于這一算法開發了Grasshop?per平臺下的MAGNETIZING FLOOR PLAN GENERATOR插件。他們不再嘗試以圓形或球體來代表房間或區域節點所占據的空間來參與粒子－彈簧系統的計算，而是改用矩形，如圖6，并且基于格網系統來進行計算，這樣更能滿足生成結果的使用需求。他們也開發了一個基于粒子－彈簧系統生成結果的交通空間生成算法，大大提高了生成結果的可用性。

圖6 MAGNETIZING FLOOR PLAN GEN?ERATOR插件的生成結果（圖片來源：EGOR G等人，2020）

2.2 從對偶圖視角出發的研究

在研究過程中，主要是以圖結構中的邊作為切入，核心要處理的問題是在幾何階段中，如何將只帶有拓撲信息對偶圖的關系與實際地塊或區域形狀相結合。

從對偶圖的視角出發的相關研究，思路和方法相較于從關系圖出發的視角要豐富很多，也沒有形成較為成熟的方法路徑。從對偶圖視角出發的相關研究，大多是通過借鑒圖論方面的研究成果，針對建筑領域中圖結構的應用，提出適合建筑領域要求的特異性方法。

Grason[9]首先將NEWS節點融入到圖結構的計算中去，并且將拆解圖結構形成子圖的思路應用在對于對偶圖的計算當中。研究通過將無方向圖結構中的邊賦予兩種不同的方向，并計算每個節點所接收和發出的邊，由此將圖結構的拆解成x和y方向上的兩個子圖。進而將對偶圖映射成正交矩形剖分如圖7。

圖7 圖結構的拆解與節點所接收和發出的邊的計算（圖片來源：GRASON J，1971）

Roth[10]借鑒和發展了Grason的思路，對于不是完全圖的輸入，利用剖分算法變為完全圖，解決了Grason算法不能處理的情況。然后利用圖結構中的邊，實際上表示與這條邊相關聯的節點在實際幾何圖形中的一個邊緣這個原理，將兩個子圖分別對應成x軸和y軸方向上的墻體，墻體的長度由邊的權重進行定義，進而將完全圖映射成正交式的四邊形房間，從而將可平面圖（a planar graph）轉化為建筑平面輪廓。同時圖中邊帶有長度屬性，可以作為四邊形房間墻體的長度，如圖8。

圖8 X和Y方向的子圖以及對應邊的計算（圖片來源：ROTH J等人，1982）

Shekhawat[11]將圖結構中的節點轉變為矩形，從第一個節點開始與后面的節點進行連接，如果一個節點需要連接兩個或以上的其他節點，那么就將這個節點對應的矩形進行水平或者垂直方向上的擴展，直到最終繪制完全部的節點后，再對圖中空缺的部分，進行額外的填充。這種方法可以看作是對J Roth方法實現的一種變體，如圖9。

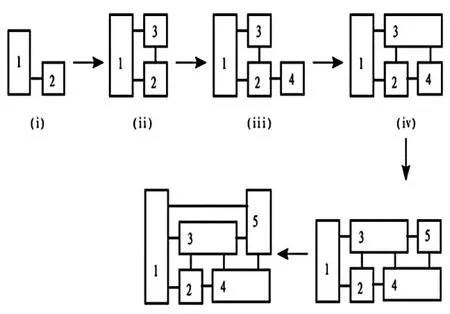
圖9 水平或垂直擴展的示意圖（圖片來源：SHEKHAWAT K等人，2020）

3 結語

對于上述提到的兩種視角，可以做出如下總結，如下表所示。

從關系圖出發的視角，因為關系圖與建筑師常用的平面功能泡泡圖的天然對應關系，所以其實現過程可以很容易被建筑師和使用者理解和想象，從規則復雜程度上來說，較為直觀且不復雜。因此，導致這種視角指導下的具體實現路徑也較為清晰，從一定程度上來說比較單一。由于其求解過程中的迭代屬性，從關系圖出發的視角方法在處理復雜約束條件的情況時（如參與拓撲關系計算的對象變多時），其求解速度下降較為明顯，并且求解結果有時會出現難以收斂的情況。另外，由于代表關系圖中點的元素（如圓形、矩形）的初始位置常常是隨機布置的，所以在對于解空間的搜索效率并不高。最后從泛用性的角度來看，由于過程中許多參數（如吸引排斥力的強度等）常常是需要反復調整的，并且是針對特定約束條件的，導致整個系統的泛用性較差。

對于從對偶圖出發的視角，因為存在從關系圖到對偶圖的轉換過程，常常導致從對偶圖出發的思路相對來說不容易直接進行想象和理解。從規則的復雜程度上來說，相較于關系圖視角下只需要布置頂點這一要素，對偶圖視角需要同時考慮頂點要素和邊要素的布置，因此在規則的復雜程度上較高。在計算的過程中，從對偶圖出發的思路常常會選擇對原本的復雜圖結構進行拆解，降低復雜程度，因此在處理復雜約束條件表現更好。另外因為其很少需要對布局位置進行精確確定，只需確定大概的方位和范圍，所以從效率的角度上來說相對較高，整體的生成過程泛用性也較好，但是從結果的角度看，不確定也導致了結果的均質性。

總的來看，關系圖視角下的探索已經處于較為完善和成熟的狀態，具體的技術實現路徑也基本上大同小異，缺乏本質上的區別。基本實現了從概念原型的開發到實際案例應用的整個流程。并且從關系圖視角出發的前提假設是房間或建筑體量是可以被視為均質的圓形或矩形的，但這個假設本身是否合理值得商榷。而對偶圖視角下的探索還不是十分完善，目前已有的研究是比較偏概念原型方面的研究，缺乏針對實際案例的應用。具體的技術實現路徑上也差異較多，但都受限于對偶圖本身幾何信息的匱乏，導致從結果上看，基本局限于矩形和正交體系。因此，從對偶圖出發的視角要解決的關鍵問題是如何實現抽象拓撲圖映射到實際幾何對象，在這個過程中要豐富和完善缺失的幾何信息。

圖結構與拓撲關系相關研究的兩種思路的分析對比表（表格來源：作者自繪）