立足于核心素養的大單元教學設計策略
——以人教A版必修一“三角函數”單元為例

哈爾濱師范大學教師教育學院 張 萌

1 核心素養培養呼喚大單元教學

新課程標準指出為全面深化課程改革，落實立德樹人的根本任務，提出未來高中數學教學中要重點突出學生核心素養的培養，并確立了六大數學學科核心素養：數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析.數學存在一般性、嚴謹性和應用廣泛性三個特征，而數學核心素養是凸顯出基本特征的思維基礎，是高中數學學習中應培養的思維品質與關鍵能力.數學知識本身的學習應不單單拘泥于知識本身的掌握，更應強調學習者頭腦中數學思維結構的形成，滲透并影響學習者思考問題的方式.因此，高中數學教學需以發展學生核心素養為落腳點進行教學，但是在大多著眼于獨立課時的實際課堂教學中，知識獲取過程中深度學習缺失，數學核心素養的高效發展顯得尤為困難.基于此，以注重知識整體結構、樹立整體性思想為出發點，進行大單元的整體教學就顯得尤為必要了.

2 大單元教學設計理念

大單元教學設計理念可在“碎片化”的課時之間建立聯系，按照知識的邏輯性與系統性逐步實現結構化的教學，突出知識框架的建立，促進知識結構化，使深度學習真實發生.數學核心素養的形成是一個循序漸進的過程，對數學知識本身的熟練掌握，并不代表學生數學核心素養的有效形成.在傳統的課堂教學中，往往將教學重點放在知識點本身，忽略了知識系統的整體性與連續性.因此，需要將對單獨課時知識點的關注，轉為對單元性整體知識的關注，改變知識的碎片化教學，令知識的學習更加系統，如此有益于學生掌握知識內核，發展數學核心素養.

3 教學設計實施策略

大單元教學設計要求我們將重點放在整體單元上，可以是某一知識體系的大單元，可以是教材中的自然單元，而自然單元中的具體課時，將其看作是一個“小單元”.總而言之，確定“單元”的內核便是整體思想，注重系統性與連貫性，突出學習者的學科能力與知識遷移水平的提高.同時需要站在課程標準的角度，基于教材，重整結構，把握學情，梳理單元知識點的明線與暗線，架構單元知識框架，削枝強干[1].

我們將確立下來的“大單元”看作是一個“生態系統”，單元環境下一環扣一環的知識鏈如同“生態系統”中存在的生物圈，它們彼此獨立又相互聯系，突出反應學科的主要觀念、思維方式和本質；并延伸出來小的“生態系統”，它們依托于大“生態系統”并受到制約，又各自存在著特性[2].大單元設計結構與生態系統的形式有著異曲同工之妙，每一個確立下來的大單元均包含著知識“小系統”，每一個系統都具有自身的特征、要突出培養的能力以及暗含的主線，并均服從于大教學的單元目標，最終達到培養學生核心素養的目的.因此，筆者將大單元教學設計策略大致分為四點，思維導圖如圖1所示.

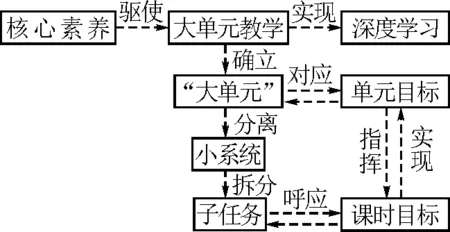
圖1

3.1 梳理單元知識結構，確立核心素養培養

為體現單元教學設計理念的優點，即教學中突出知識的整體性與系統性，讓學生更好地掌握單元知識框架，需要以新課程標準為指南，重新梳理教材的單元知識點，確定以單元為指向的單元目標和各獨立課時指向的課時目標，并結合學生的思維構建特征與心理特征，確立學生所要發展的核心素養.

三角函數隸屬于高中函數主線，因此研究方法應遵循函數的整體研究方法.函數主線的研究首先是整體把握函數概念的來源與延伸，繼而對函數的“共性”性質進行系統研究；結合具體函數深入研究其幾何性質與代數關系，最后利用函數模型解決生活情境中的實際問題.因此，教師教學應結合函數主線的一般研究路徑與課程標準的要求，明確對三角函數“大模塊”的整體設計要求，建立知識小系統[3].利用單位圓建立三角函數的概念；運用幾何直觀與代數運算得到三角函數的各類性質，以及三角函數間的恒等關系；利用三角函數模型解決實際問題；等等.突出發展學生數學抽象、邏輯推理、直觀想象、數學運算和數學建模等數學學科核心素養.

3.2 立足主線削枝強干，制定大單元的小系統

依據本單元教學設計所確立下來的單元目標，遵循此目標與對學生的培養方案，分離單元目標并進行重組，確定含有邏輯依據的小系統，將各個小系統串聯起來，加強知識與方法的聯系和遷移，突出學習者頭腦中知識內核的框架形成[4].

小系統一：突出單位圓暗線，周期性串聯知識.

三角函數中各概念的生成與確立，均離不開單位圓發揮的重要作用.在引入弧度制的過程中，便已經向學生滲透了單位圓，并從單位圓上點的運動規律出發形成三角函數的概念.同角三角函數的基本關系式與誘導公式，以及承接其的三角恒等變換公式，均以單位圓為依托.因此，“單位圓”作為一支暗線貫穿著三角函數的概念及公式學習，同時借助單位圓這一直觀圖形，建立數與形的聯系，以形貫數，以數融形，發展學生直觀想象核心素養.

小系統二：結合經驗與明暗線，性質歸為大概念.

以三角函數的定義為出發點，對三角函數的一系列性質的研究，可模仿基本初等函數的基本性質的研究路徑.結合單位圓與三角函數的周期性這一特點，從單位圓上任意一點出發，明確各類三角函數的圖象，并借助圖象深入獲得三角函數更多的延伸性質.因此在對子任務的設計上，將三角函數的各類性質看成一個整體模塊，以單位圓為載體，以三角函數圖象為橋梁，逐層遞進滲透三角函數的性質.將性質看作一個系統的同時，貫通瑣碎的知識點形成性質模塊，并從中深入探究，選取適當的研究方法，發展學生直觀想象、數學運算等核心素養.

小系統三：深化三角函數模型，加強核心素養的發展.

數學建模是對現實世界中的問題進行抽象解析后，合理地運用數學方法解決實際問題.由于三角函數本身就具有區別于其他函數的顯著性質——周期性.于單元初始引入現實中大量的周期變化現象，為解釋這些現象并解決問題，就需要用不同于以往的函數進行刻畫，進而導出周期特性強的數學模型——三角函數.本單元對學生數學建模核心素養的培養，要引導學生經歷實例，分析問題，建立三角函數模型，解決典型的周期變化的實際問題，并在滲透建模思想、發展數學建模核心素養的同時，加強與其他學科的聯系，發展學生的跨學科素養.

3.3 拆分單元小系統，確立系統子任務

子任務的確立與設計均服務于小系統，受小系統主題的制約，并立足于核心素養，實現單元教學目標.子任務確立后可與課時目標銜接，并利用信息技術手段以及跨學科聯系，加強對單元框架以及研究路徑的掌握.

對于小系統一，以周期性和與之對應的具有旋轉對稱周期性的單位圓為主線，單刀直入提出問題并探究，直截了當引出概念.設置任務一：建立周期大情境，引出弧度新概念.立足于三角函數的周期性，并以圓周運動為周期現象變化規律的載體，以此利用幾何直觀引入弧度制的學習，并以小任務為指引確立課時目標.依據系統設置任務二：周期變化引概念，單位圓建立聯系.以弧度制滲透的單位圓為基礎，受特殊變化規律的周期性指引，從實際問題的要求出發，利用單位圓上點的坐標與三角函數建立聯系，將教學重點放在把握周期性與三角函數的本質上，實現現實問題數學化的過程，提升學生對概念的掌握程度.設置任務三：定義出發新探究，溝通幾何建聯系.從三角函數的定義出發，以數形結合為手段，得出三角函數的各類性質，突出圓的幾何性質的直觀反應，依次銜接與概念有關的各類三角函數的關系式.合理設置對單位圓上點坐標的探究活動，運用幾何關系得出三角函數的一系列基本關系式，加強內在聯系.最后設置任務四：幾何性質代數化，對稱出發探公式.依據單位圓及其對稱性，改變單位圓中任意角終邊的位置，探究角的終邊上點的坐標變化，從而將變化規律進行抽象，實現幾何特征代數化，完成誘導公式的學習.

對于小系統二，將三角函數的一系列性質看作一個整體模塊，根據函數主線研究性質的一般路徑，進行教學設計.在掌握三角函數性質的基礎上，掌握研究性質的一般思想與方法.首先設置任務一：動態關聯生圖象，舊有思路得性質.根據小系統一中單位圓的引導，由單位圓上特殊點對應生成圖象中的特殊點，并充分利用信息技術，將單位圓上點的變化與三角函數圖象上的點實現對應，得到三角函數的圖象.如此加強知識的聯系，單位圓的應用不僅能突出本章知識點之間的緊密聯系與系統性，更能突出性質來源的直觀性，加強對知識點的理解.其次設置任務二：正切性質聯定義，總結經驗破難點.正切函數性質的研究較正余弦函數難度更大，更難尋找切入點.因此需從定義入手，結合研究函數圖象與性質的經驗，將定義與已研究的部分性質加以聯系，進一步借助圖象運用數形結合思想探究其他性質.然后設置任務三：旋轉對稱生公式，類比推導成系統.任何公式都不是孤立存在的，因此公式的推導要從根源入手，如此可減少公式證明的繁瑣流程，加強公式證明的一般性.從圓的旋轉對稱性與三角函數間的緊密聯系入手，設計開放式探究，讓學生進行自主思維活動形成公式.而后類比兩角差的余弦公式的研究思路，推導出其余公式，突出公式內部的系統性，使得公式與三角函數的性質聯系更緊密.最后設置任務四：基于公式等變換，換元逆向重思想.承接三角函數性質的研究，重點放在公式的應用上，以需求為基點，呼喚公式的誕生，并重點關注變換目標，明確目的，重視變換過程.突出換元、化歸等數學思想方法的應用，發展學生數學運算、邏輯推理等核心素養[5].

對于小系統三，為突出數學建模思想的滲透，加強學生對數學建模的理解，并為高等數學打好基礎，培養綜合應用知識解決問題的能力.初步設置任務一：具體圖象引思考，初步總結新思路.從勻速圓周運動入手，滲透數學建模意識，與單位圓的旋轉對稱性建立聯系，加強知識的連貫性和系統性.以三角函數的圖象和性質為基礎，改變三角函數解析式的形式，運用信息技術手段對形如“y=Asin(ωx+φ)”的函數設置探究活動.設置任務二：動態直觀顯意義，信息技術重探究.結合勻速圓周運動模型，將對函數圖象的具體探究與函數解析式緊密聯系起來，運用信息技術更加直觀地呈現圓周運動與函數解析式的關聯性，并引導學生進行自主總結，在探究活動中突出數學建模思想.最后設置任務三：跨越學科樹模型，解決問題培能力.此任務重在從模型出發培養學生解決實際問題的能力，引入跨學科情境，在實際問題的催化下，加強對三角函數周期性模型的使用，并將整個探究活動的重點放在學生的自主學習中，體會模型的特性，提高數據整理與總結能力，在培養學生數學建模核心素養的同時，發展跨學科素養.

3.4 構建測評系統，突出教學設計目的

由于大單元教學設計重在突出單元知識的系統性、課時知識間的銜接性以及模塊知識間的整體性，實施起來并不容易，故而設置適當的測評體系就尤為重要.評價反饋環節首先需對基于單元目標下的學生核心素養的培養情況進行檢測，在檢測的同時加強學生對單元知識結構框架的掌握，深入知識系統.教師需細致觀察學生知識能力與水平能力的提升情況，對確定的單元教學設計環節進行適時地修改，及時將定位不明確的教學設計回歸正位，形成知識網絡，達到內容形式交融、方法素養滲透的最終教學目的，發展學生數學核心素養.

4 結語

最后，在新課改的需求下，立足于培養學生數學學科核心素養的教學設計理念變得越來越必要.大單元教學設計突出對學生能力與核心素養的培養.學生核心素養的不斷提升，不僅對單元知識點的掌握具有莫大的益處，在未來的學習之路上同樣大有裨益.因此，立足于學科核心素養的大單元教學設計是學科教育落實立德樹人、發展素質教育、深化課程改革的必然要求，也是學科核心素養扎實落地的關鍵路徑.對大單元教學設計的學習不能停歇，探索也要永不停止[1].