基于范希爾幾何水平理論的平面與平面垂直的教學設計

哈爾濱師范大學教師教育學院 錢月瑩

1 范希爾幾何思維水平

20世紀50年代，荷蘭學者范希爾夫婦提出了幾何思維發展理論，并劃分為5個水平，被稱為范希爾理論.根據學生理解和幾何知識把思維水平分為以下5個層次.

水平1：視覺.兒童在面對圖形時，可以大致地區分出圖形的差異，但不能具體指出圖形的類別.

水平2：分析.圖形的外觀以及相似之處，學生是可以總結出來的，也能據此解決一些簡單問題，但不能建立其中的聯系.

水平3：非形式化的演繹.通過學習，學生理解圖形所具有的性質以及概念等，但不能對此進行邏輯推理.

水平4：形式化演繹.這個階段的學生建立起知識之間的聯系，并能進行推理，了解“定義”“公理”“定理”“性質”的內涵與外延.

水平5：嚴密性.學生能在不同的公理下嚴謹地建立定理，以分析比較不同的幾何系統，如歐式幾何和非歐氏幾何系統的比較[2].

根據幾何思維的5個水平，范希爾夫婦提出了學生思維水平進階(即從一個水平到下一個水平的發展)的5個教學階段.

階段一：學前咨詢.通過交流的形式，教師了解學生儲備的基礎知識，學生知道本節要學習的重點內容.

階段二：引導定向.通過簡短的問答交流，教師要根據學生的自身發展水平安排本節的教學任務，使學生明白幾何學習的方向和方法.

階段三：闡明.教師利用專業的術語講解本節的重點內容，學生要調動自身的儲備知識理解本節的概念、命題等.

階段四：活動.教師在此階段中不斷激發學生的學習興趣，使學生通過解決不同的問題，夯實本節重點內容.

階段五：整合.學生自己整合本節所學的內容，豐富自身的知識儲備，構建完整的公理化系統.

范希爾理論中教學設計的主要目的是促進學生幾何思維水平的提高，特別是培養學生空間想象、解決問題等能力[3].

2 “平面與平面垂直”教學設計

本節課主要按照“背景-二面角(定義、表示、度量等)-特例(直二面角)-兩平面垂直”的順序進行安排，并把重點放在兩個平面垂直的研究上[4].

2.1 階段一：學前咨詢

學生通過前面的學習已經有了一定的知識積累，在探索中學到的研究思路也為本節課的學習打下了堅實的基礎.因此，教師在講授新課之前回顧“線面平行、面面平行、線面垂直”的研究路徑是極其重要的.

問題1通過前面的學習，我們已經研究了幾種空間線面位置關系.你認為接下來要研究什么位置關系呢？應該遵循怎樣的研究步驟呢？

學生活動：研究平面與平面垂直的位置關系.應該遵循直線與平面垂直的研究步驟.

追問：我們是怎樣研究直線與平面垂直的呢？你能總結出這幾種位置關系研究步驟的共同點嗎？

學生活動：都遵循“現實背景-位置關系的定義、表示-判定-性質”的研究路徑.

設計意圖：引導學生回顧之前的內容，為接下來要講授的“平面與平面垂直的判定”作鋪墊.在這個過程中，最重要的是研究方法的展現，教師可以通過類比的思想方法帶領學生在新課學習中逐步完善知識系統，為“平面與平面垂直的判定”的研究指明方向.

2.2 階段二：引導定向

問題2在研究空間垂直關系時，線線垂直是研究的基礎.在平面幾何中，為了研究線線垂直，引入了角的概念，當直線與直線的夾角為90°時，則稱兩直線垂直.為了定義空間兩個平面互相垂直，需要先定義“空間中兩平面的夾角”.類比平面幾何中線線垂直時夾角的定義，我們應該如何定義空間中兩平面的夾角呢？

學生活動：在教師的引導下，學生逐步體會到要研究兩個平面相交的位置關系，需引入二面角的概念，進而研究“平面與平面垂直”.

追問：該如何定義二面角呢？

師生活動：教師帶領學生思考二面角的研究思路，并向學生展示圖書翻頁，從生活中的實例出發，由學生自主概括出二面角的概念，教師要規范學生的作圖方式及符號表示.

圖1

二面角：如圖1所示，從一條直線出發的兩個半平面所組成的圖形叫做二面角，這條直線叫做二面角的棱，這兩個半平面叫做二面角的面.棱為AB，面為α，β的二面角記作二面角α-AB-β.有時為了方便，也可在α，β內(棱以外的半平面部分)分別取點P,Q，將這個二面角記作二面角P-AB-Q.如果棱記為l,那么這個二面角記作二面角α-l-β或二面角P-l-Q.

問題3在生活中，室內溫度較高時，我們會說“把窗戶打開點，讓風吹進來”，這是指什么角大一些？二面角與平面中的角都是具有大小的，應如何度量二面角的大小呢？

學生活動：學生在教師的引導下回顧平面幾何中異面直線所成的角、直線與平面所成的角，都是由“平面角”推出來的.學生有所啟發，意識到“二面角”可以轉化為“平面角”進行度量.

追問1：二面角的平面角具有哪些性質呢？與“線面角”的平面角有什么關聯之處嗎？

學生活動：它們具有相同的性質.棱是連接兩個半平面的“橋”，平面角的頂點應位于棱上.角的兩邊分別位于兩個半平面內，并且與棱的位置關系是唯一確定的.

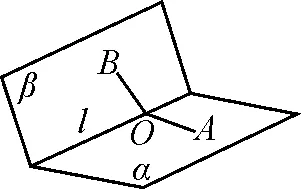
圖2

二面角的平面角：在二面角α-l-β的棱l上任取一點O，以點O為垂足，在半平面α和β內分別作垂直于棱l的射線OA和OB，則射線OA和OB構成的∠AOB叫做二面角的平面角(如圖2).

追問2：二面角的平面角有什么性質呢？

師生活動：教師帶領學生歸納出以下幾點性質.(1)角的頂點在棱上，角的兩邊分別在兩個半平面內，角的兩邊分別與棱垂直；(2)二面角的平面角大小與點O在棱l上的位置無關；(3)平面角是直角的二面角叫做直二面角，二面角的平面角θ的取值范圍是0°≤θ≤180°.學生要對這幾點性質反復推敲，增強印象.

設計意圖：二面角的概念與角的概念具有很強的類比性，通過生活中的實例引入，將學生的直觀認知推向理性認知，帶領學生把二面角轉化為平面角進行度量，并讓學生自主歸納出二面角的平面角的性質，加強學生對知識的理解，構建完整的知識體系.

2.3 階段三：闡明

問題4類比空間兩條直線相互垂直的定義，你能給出平面與平面垂直的定義嗎？

學生活動：教師起到輔助作用，讓學生類比出平面與平面垂直的定義.

圖3

面面垂直：兩個相交平面構成的二面角是直二面角，則稱這兩個平面互相垂直.平面α與β垂直，記作α⊥β(如圖3).

設計意圖：通過給出二面角的定義及性質，為平面互相垂直的定義作鋪墊，引發學生探索性思考，進而使學生感受到數學定義的形成是具有過程性、科學性的，增強學生的邏輯推理能力，開發直觀想象能力.

問題5研究了兩個平面相互垂直的定義，在此基礎上，應該研究什么呢？

學生活動：應該研究平面與平面垂直是如何判定的.

追問1：在蓋房子時，工人們都會測量墻面與地面是否垂直.由此，他們會用一根系有重物的線來檢測，若細線與墻面是緊貼的，則墻面與地面是垂直的，否則是不垂直的.這種測量方法運用了什么原理呢？

學生活動：學生以小組的形式討論，得到結論，即如果墻面經過地面的垂線，那么墻面與地面垂直.

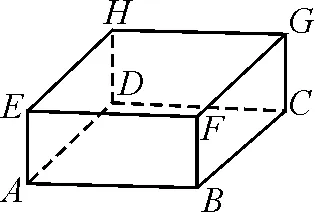
圖4

追問2：這種結論在長方體中是否也成立呢？如圖4，在長方體ABCD-EFGH中，怎樣證明平面ABCD垂直于平面ABFE呢？

學生活動：在長方體中也是成立的.平面ABFE經過平面ABCD的一條垂線AE，所以平面ABCD垂直于平面ABFE.

經過師生討論，總結出兩個平面垂直的判定定理：如果一個平面過另一個平面的垂線，那么這兩個平面垂直.(即線面垂直?面面垂直.)

設計意圖：從建筑師傅砌墻的生活實例入手，向同學們拋出要證明的問題，激發學生的興趣，讓學生由表及里，發現數學的核心內容，培養數學思維.

2.4 階段四：活動

學生對本節知識已有了一定的了解，但把重點內容應用到實例中，以及更深層面的學習，仍存在一些欠缺.因此，要設置例題，夯實學生的基礎.

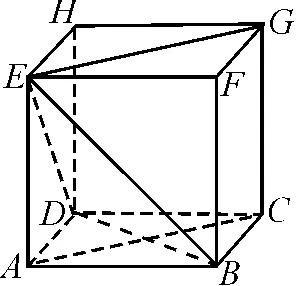
圖5

例如圖5所示，在正方體ABCD-EFGH中，求證：平面EBD⊥平面ACGE.

證明：在正方體ABCD-EFGH中，AE⊥平面ABCD，BD?平面ABCD，

∴AE⊥BD.

又∵BD⊥AC，AC∩AE=E，

∴BD⊥平面ACGE.

∵BD?平面EBD,

∴平面EBD⊥平面ACGE.

設計意圖：本例題與本節課所學的重點知識密切相關.要證明面面垂直，首先要找到線面垂直，這是一個思維轉化的過程.發揮學生的主體作用，促使學生體會數形結合在解決數學問題中的重要作用.

2.5 階段五：整合

問題6通過本節課的學習，你都收獲了什么？

追問1：怎樣才能測量出二面角的大小？兩上平面垂直的定義是什么？怎樣用符號和圖形表示？兩個平面垂直的判定定理是什么？是怎么得到的？

學生活動：小組進行討論，回答追問1的問題.

(1)二面角，二面角的平面角的定義，兩個平面垂直的定義，兩個平面垂直的判定定理(線面垂直?面面垂直).

(2)數學思想方法：類比、轉化、降維.空間位置、數量關系→平面位置、數量關系[5].

設計意圖：學生學習完本節知識，可能存在部分概念掌握不全面的情況，需要及時查缺補漏.這個階段，要讓學生自主回答，充分體現學生的主體性，并讓學生體會類比、轉化等思想方法，培養數形結合、邏輯推理、思維轉換等能力.

3 總結

平面幾何與空間幾何知識，對于學生來說都是較難理解的.學生缺乏直觀想象、邏輯推理等能力，只是簡單了解公式、定理等，并沒有學會其中的思想方法.依據范希爾理論進行“平面與平面垂直的判定”的教學設計，教師能更好地了解學生的思維發展現狀，設計出科學合理的教學方案，培養學生的創新能力以及應用意識.