高等數學創設 初等數學解決
無錫市太湖格致中學 何 勇
在一些高考數學試題或模擬題的設置中,以創新情境等方式來巧妙設置,利用高等數學的知識來創設或應用,是新課標高考數學命題的一常見命題方式與創新亮點,倍受各方關注.此類創新應用問題,合理滲透初等數學與高等數學之間的聯系,實現中等教育與高等教育之間的合理有機過渡與無縫銜接.
1 創新定義類問題
利用高等數學中一些概念、名稱、相關知識等的初等數學化創新定義,通過初等數學知識來重新簡單定義高等數學問題,結合合理推理論證或數學運算,實現用初等數學知識解決創新問題的目的.
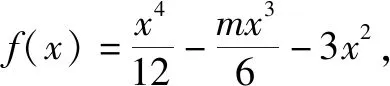
A.4 B.3 C.2 D.1
分析:根據題目條件中給出的“凸函數”的創新定義,通過對給定的函數f(x)進行二次求導,結合二階導函數在給定區間上的不等式恒成立進行等價轉化,變換主元,將二次不等式恒成立問題轉化為一次不等式恒成立問題,結合一次函數的圖象與性質來確定變量的取值范圍,進而確定區間“寬度”的最大值.

根據“凸函數”的定義,當|m|≤1時,f″(x)=x2-mx-6<0恒成立,等價于當|m|≤1時,關于m的一次函數h(m)=x2-mx-6<0恒成立.
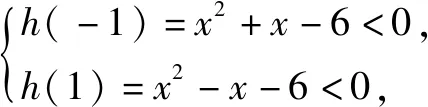
從而b-a的最大值為2-(-2)=4.
故選擇答案:A.
點評:借助高等數學中的“凸函數”進行創新定義,結合初等數學中一些基本初等函數的求導與運算,綜合函數與方程、函數與不等式的轉化與應用,利用函數的圖象與性質實現問題的突破與解決.以創新定義的形式來實現高等數學知識與高中基本初等函數之間的鏈接.
2 公式應用類問題
利用高等數學中一些定理、性質、公式等的初等數學化表示,結合初等數學知識來展開與構建,合理利用推理論證或數學運算,實現借助高等數學知識簡單快捷解決一些初等數學問題的目的.
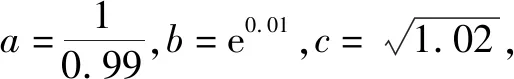
A.a>b>cB.b>c>a
C.b>a>cD.c>b>a
分析:根據題目條件,合理聯系條件中分式、指數式、根式等對應的泰勒公式,利用泰勒公式的展開式所對應的關系式的結構特征,快捷解決對應代數式的大小比較問題.
解析:根據泰勒公式,得
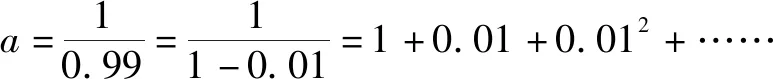
由上各展開式的關系,可知a>b>c.
故選擇答案:A.
點評:借助高等數學中的泰勒公式,利用泰勒公式的展開,并結合三個代數式在泰勒公式條件下的進一步轉化以及相應的結構特征,可以簡單快捷地比較大小.泰勒公式是高等數學中的內容,是高中數學知識的拓展與課外提升部分,是高中數學競賽中的知識點.
3 步驟分解類問題
利用高等數學中一些解題步驟、技巧策略等的初等數學化分解,在初等數學背景下按部就班,通過初等數學知識來合理推理論證或數學運算,實現用初等數學知識解決高等數學問題的目的.
例3(福建省莆田市2022屆高中畢業班第二次教學質量檢測數學試卷·12)(多選題)意大利數學家卡爾達諾(Cardano. Girolamo,1501—1576)發明了三次方程的代數解法.17世紀人們把卡爾達諾的解法推廣并整理為四個步驟:
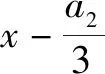
第二步,利用公式x3+y3+z3-3xyz=(x+y+z)(x+ωy+ω2z)(x+ω2y+ωz)將x3+px+q因式分解;
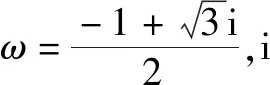

某同學利用上述方法解方程8x3-12x2-42x+55=0時,得到y的一個值:-1+i,則下列說法正確的是( ).
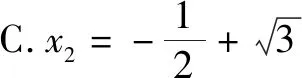
分析:根據題目條件,結合卡爾達諾的三次方程代數解法的四個步驟的說明與理解,按部就班,逐一展開與分析,綜合復數的四則運算加以計算與處理,進而確定對應說法的正確性.

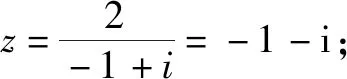
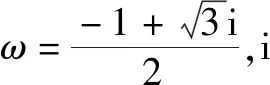
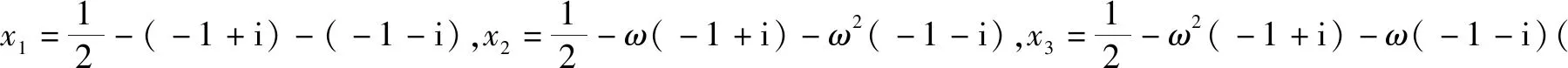
綜上分析,故選擇答案:ABC.
點評:借助高等數學中卡爾達諾的三次方程代數解法的步驟分解,結合數學運算、代數式的變形、因式分解以及復數的四則運算等的綜合應用.此類問題涉及高等數學中的一些解題步驟的初等數學分解,關鍵就是按照說明按部就班,綜合推理論證或數學運算加以解決.
通過高等數學中的某個數學概念的初等化定義或初等化應用、某個定理公式的展開與應用、某個解題步驟過程的初等化分解等創新設置,實現高等數學知識初等化,借助定義的理解、公式的應用、步驟的分析等加以拓展,從而實現相關知識在內涵與外延上的突破,考查學生的閱讀理解能力、推理論證能力等,也對學生后續進入高校學習所具備的基本能力加以合理區分與選拔.

