在數學思想方法的指導下構建高效復習課堂
甘肅民勤縣教師進修學校 運其書
近幾年來,高考已將數學思想方法的考查作為一項重點內容,為此,在高三復習階段應重視學生數學思想方法的滲透,化思想為動力,化方法為能力,構建高效數學課堂.筆者在高三復習階段做了一些嘗試,取得了一些效果,以期拋磚引玉,共同成長.
1 復習基礎,優化認知結構
基礎知識的復習和鞏固是高三數學復習的一項基本任務,是學生成績提升的前提保障.在復習基礎知識時,應注意揭示和總結重要的數學思想方法,進而使基礎知識更加豐富、生動,從而激發學生的復習熱情,促進復習效率提升[1].
例如,在復習指數函數y=ax和對數函數y=logax時,應滲透分類討論思想,引導學生關注底數a分為a>1和0 很多數學知識間存在著一定的關聯性,為了知識間可以更好地溝通和聯系,在梳理知識時就要滲透數學思想方法,發揮其紐帶的作用,幫助學生科學地建構知識體系,進而優化學生認知結構,提升學生綜合素質. 函數思想作為重要的數學思想,不僅在解決函數問題時有著重要的應用,而且也有效地溝通了方程和不等式,為此,將三者合理地聯系與轉化,極大地豐富了原有認知,有利于知識的遷移和轉化.另外,運用數形結合思想將函數圖象與方程、不等式的解緊密相連,有利于實現數學知識的優化和整合,有利于解題效率的提升. 因此,在高三階段,要重視數學思想方法的滲透和提煉,進而將不同模塊的知識通過聯想和轉化進行有效的重組,逐漸建立系統的、全面的認知體系,進而提高學生的綜合應用能力. 解題教學是高三復習階段的重點課型,通過解題反饋的信息及時查缺補漏,可有效提升學生解題能力.解題過程實質就是通過合理的聯想和轉化將題設信息與結論建立聯系,運用分類討論、數形結合等數學思想進行加工和分析,進而逐漸縮小題設信息和結論的差異,找到合適的切入點,高效求解問題[2].在解題過程中合理運用數學思想方法是解題的關鍵,有利于解題策略的優化,有利于解題效率的提升. 分析:本題若從代數的角度求解,不僅計算比較復雜,而且容易出現思維障礙,仔細觀察式子特征不難發現其與兩點間的距離公式息息相關,為此通過挖掘題設的幾何意義,運用數形結合思想將代數問題幾何化,從而為順利求解帶來了便利. 通過解題過程容易發現,靈活應用數形結合思想使代數問題幾何化,進而應用平面幾何的相關知識順利地求解了問題,培養了學生數形建模能力. 很多數學問題都存在一定的規律,若不關注規律,很容易將思維引入死胡同,不僅難以求解,而且容易挫傷學生的學習信心.例2的求解過程是先從特殊出發,發現了隱藏于結論中的一般規律,通過充分聯想推理出了f(x)+f(1-x)=1.通過特殊到一般的轉化,學生的思維豁然開朗,解題思路也應運而生. 例3若不等式(lgx)2-(2+m)lgx+m-1>0對|m|≤1恒成立,求x的取值范圍. 分析:觀察題設信息,學生易于將不等式看成關于lgx的二次不等式,但求解時不僅需要分類討論,而且運算復雜,即使能夠求解也需要較長時間,顯然這種方法是不可取的,為此需要另辟蹊徑.既然將lgx看成未知難以求解,是否可以將其視為已知呢?將常量和變量進行轉化,將不等式轉化為關于m的一元一次不等式,于是構造函數f(m)=(1-lgx)m+[(lgx)2-2lgx-1],這樣將主參換位有效地規避了繁瑣的討論,使其轉化為常規問題,此時求解x就變得簡單方便了. 可見,在面對復雜的數學問題時,合理轉化可以實現化繁為簡.在高中數學教學中滲透數學思想,可以有效地避免思維定式給解題帶來的局限性.有時候通性和通法不適宜問題求解時,要學會變通,及時轉換思路,這樣往往可以收獲意外的驚喜. 數學問題是千變萬化的,在解題過程中靠死記硬背不僅學得累,而且很難提升解題效率.若想既快又準地解決問題,就要重視培養思維的變通性,即當固定方案行不通時,需要重新觀察和挖掘題設信息,通過聯想和分析知識點間的相關性,尋找最優解決方案[3].要完成這一過程需要注意訓練以下幾種能力. (1)觀察 解題首先要通過觀察提取有價值的信息,進而通過對信息的整合找到解題的合理切入點.數學條件和數學關系或顯性或隱性地蘊含于題目中,要想解決問題就要依據題目的結構特征,通過深度觀察和剖析,找到問題的本質特征,進而確立解題思路.在解題時切勿急于求成,要善于從整體去觀察和解讀.如果看到題目就解,解不下去再更換思路,這樣將嚴重影響解題效率.為此,解題時要進行細致、透徹地觀察,厘清問題的來龍去脈后再求解,這樣可使解題更高效. (2)聯想 聯想是通往成功的必經之路.眾所周知,高中數學題目是復雜的,在解決一個問題時往往會涉及到很多內容,而這些內容的聯系往往并不明顯,通過觀察找到題設的特征后,應用聯想將這些相似、相關的內容串聯起來,形成一個較為完善的思維脈絡,靈活應用所學知識進行遷移和轉化,巧妙解決問題. (3)轉化 轉化是解決數學問題的法寶.大多數學問題都是在轉化中完成的,例如,當遇到比較復雜的問題時常將其進行拆分,將其轉化為較為熟悉的、簡單的問題,進而化繁為簡;當遇到比較抽象的內容時,常與生活實踐相聯系,從而在具體的情境中進行聯想和轉化,使問題化抽象為具體.當然還有化未知為已知,化新知為舊知,等等.總之,在解題時要通過合理聯想尋求轉化關系,才能高效解決問題. 數學思想方法蘊含于不同的基礎知識之中,應用于不同的數學問題之中.若想讓學生明晰和領悟數學思想方法的價值,在教學中就應對數學思想方法進行及時的總結和歸納,進而通過提煉和概括強化學生對數學思想方法的認識. 例如,以數列為例,在推導等比數列求和公式時,分類討論q的值,體現了分類討論思想;在解決數列遞推問題時,常常需要應用等價轉化思想;等等.同時,在解題時還需要應用換元法、配方法等重要的數學方法.通過有效的提取,讓學生抓中解題的重點和核心,進而為合理轉化提供必要的前提. 當然,在復習階段還可以設置專項訓練,以數學思想方法為主線將相關知識進行串聯,進而在深刻領悟數學思想方法重要價值的同時,促進思維能力的不斷提升. 總之,在教學中要引導學生關注數學思想方法,使之成為優化學生認知結構,發展學生思維能力,提升學生分析問題和解決問題能力的法寶.2 鞏固練習,提升解題能力
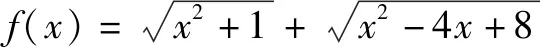
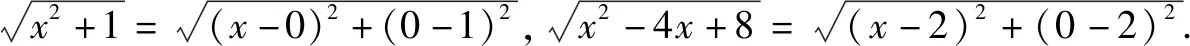
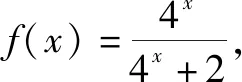
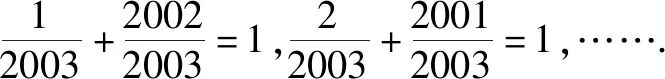
3 歸納總結,深化思想

