數學教學中滲透數學思想的幾點體會
新疆昌吉州育林中學 成東平
中學數學中的數學思想有公理化的思想,符號化的思想,等等.一般認為,在中學數學教學中,應使學生學會和熟悉的數學思想有:化歸與轉化的思想,函數與方程的思想,分類討論思想,數形結合的思想.在中學階段進行數學思想教學,有兩條基本途徑,即第一條是逐步滲透,第二條是強化訓練.下面重點談一談筆者在滲透數學思想方面的一些體會.
1 充分挖掘數學思想,在教學中進行滲透
理論教學與解題教學是中學數學教學的兩條主線,數學思想的教學應貫穿于這兩條主線之中[1].由于學生對數學思想從了解到認識,從理解到掌握應用,需經歷較長的時間,而且解題教學更側重于數學思想的應用,因此我們必須把數學知識的教學過程作為滲透數學思想的主渠道,充分挖掘教材中基礎知識部分蘊含的數學思想,盡可能創造較多的機會展現數學思想,以便學生在掌握知識的同時,逐步感知、理解數學思想的真諦.
例如,立體幾何中多面體與旋轉體直觀圖的畫法,其實是借助于平面圖形來刻畫空間圖形,通過“展開圖”將柱體、錐體、臺體的側面置于某平面,把空間曲面的面積轉化為平面圖形的面積來計算……這些看似平淡的內容,無不體現著轉化思想——空間問題平面化,教學中若因其簡單而忽視,就會失去滲透數學思想的良機.
2 精心設計教學過程,使數學思想滲透其中
滲透,即依附其上,隱含其中.滲透是指教者有心,學者無意的方式,是一個根據教學內容,反復、逐步進行的過程.滲透數學思想不是簡單地給學生灌輸一些名詞,數學思想的滲透應自然貫穿于教學過程之中,讓學生在獲取知識、掌握方法的過程中自然地受到數學思想的熏陶,達到一定火候后經老師點撥逐漸形成關于數學的基本觀點——數學思想[2].因此,教師應精心設計教學過程,充分暴露知識的發生、發展過程和解題探索過程中的思維軌跡,并引導學生積極參與這一過程,讓學生在參與中親身感知數學思想.
例如關于“祖暅原理”的教學,筆者設計了如下的教學過程.首先問學生以前學過哪些幾何體體積的計算公式,接著提出問題:“現有一塊形狀不規則的小石塊,你如何才能測得其體積?”當學生通過探究,得出“將小石塊投入盛水的量筒里,觀察水面升高了多少,計算出升高部分水的體積”的解決方法后,又提出問題:“這一解決問題的過程中蘊含了一種很重要的數學思想,你能說出它是什么嗎?”有的學生說阿基米德定律,有的學生說體積相等原理……雖答不到點子上,但大多有一種比較樸素的認識,在此基礎上老師適時點撥:將不規則小石塊的體積求解問題,轉化為圓柱體積的問題,此即化歸思想.之后,又拿出一把撲克牌,將其疊堆成長方體形狀再扭曲變形成斜平行六面體,讓學生思考變形前后體積是否相等,提出祖暅原理,不僅使化歸思想貫穿于探索問題的思維過程之中,而且使學生明白了祖暅原理的作用,為其后體積公式的推導留下伏筆.
3 揭示數學方法內涵,深化對數學思想的理解
數學思想源于數學知識和數學方法,在教學中揭示數學方法的內涵,既可以使學生對運用數學思想處理問題的具體操作方式得到更多的了解,也可以讓學生從思想的高度認識數學方法,深化其對數學思想的理解.
4 有計劃、有步驟地實施滲透
要滲透數學思想,必須深入分析教材,逐一析出各部分內容中蘊含的數學思想,并根據學生的實際知識層次、認識水平制訂出一個切實可行的計劃,何時、何處滲透何種思想,確定滲透的側重點,充分挖掘教材潛力,反復多次進行滲透,使學生在一系列的潛移默化中逐步領悟數學思想.
例如,在“復數”的教學中,有著滲透化歸思想的良好條件.因此,在此單元的教學中,筆者將化歸與轉化思想的滲透作為數學思想教學的側重點,在具體教學方式上,除在復數的概念、復數的表示形式、復數的運算等內容中逐步滲透化歸思想外,還利用一題多解突出對學生進行化歸意識的培養.比如課本中有這樣一道題:“已知z1,z2∈C,z1z2=0,求證z1,z2中至少有一個是0.”引導學生從下面幾種思路去解答.
思路1:設復數的代數式.設z1=a1+b1i,z2=a2+b2i(a1,b1,a2,b2∈R).
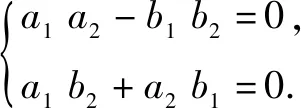
思路2:取模法.由z1z2=0,得|z1||z2|=0.
所以z1,z2至少有一個為0.
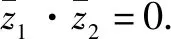

故z1,z2中至少有一個為0.
通過這三種解法的歸納,學生不難發現其相同的思想實質——復數問題實數化,而無論是“代數形式”“取模法”,還是“共軛法”都是化歸的手段.一題多解使學生對化歸思想有了較為充分的認識.
滲透,是數學思想教學的初級階段,當學生已初步形成數學思想時,就應當提供條件讓其在數學活動的實踐中進一步去領會、去掌握[3].比如,學生在解題時總是將分式問題整式化、無理問題有理化、多元問題一元化、復數問題實數化、空間問題平面化……,在這一系列具體實踐中,學生一旦悟出未知化已知、復雜化簡單的規律其實就已初步具備了化歸與轉化的思想.從這個意義上講,滲透與應用是數學思想教學的兩條基本途徑,關于如何在應用中強化學生對數學思想的認識,作為數學思想教學的另一側重點,在這里筆者不作敘述.

