考慮關節摩擦的剛柔耦合機械臂末端抖動模擬與分析
管戀哲,張振山,崔國華,潘穎
(上海工程技術大學機械與汽車工程學院,上海 201620)
0 前言
機器人作為一種典型的機電一體化產品,在現代生產生活中有十分重要的作用,其應用場景不但涉及汽車、機床等工業領域,而且在航空、醫療以及家政服務等方面也應用廣泛[1-2]。但在焊接、裝配、去毛刺等操作過程中,其末端容易發生抖動[3],從而導致機器人實際的運動性能與期望的高精度運動性能相比還有較大的差距[4]。為了滿足輕型制造任務等需要[5],對機器人的末端抖動進行研究十分必要。其中,機器人關節摩擦的存在會影響機器人控制系統的質量,從而造成系統動蕩。對于做軌跡追蹤的機械臂來說,當突然改變速度方向時,摩擦會造成機械臂較大的追蹤誤差和出現極限環振蕩[6];對于低速工作的機械臂來說,摩擦力矩的存在會造成其產生爬行現象及追蹤滯后[7],機械臂工作所需的驅動力矩大約有20%消耗在克服摩擦阻力上[8]。
山顯雷、程剛[9]以3SPS+1PS并聯機構為研究對象,基于牛頓-歐拉法,通過選取動平臺上球鉸鏈所在位置點的運動學參數作為中間變量,建立了考慮關節摩擦且具有顯式形式的動力學模型,并驗證了所建模型的有效性,所得模型可用于并聯機構的摩擦補償控制研究。段書用等[10]以六軸串聯機械臂為研究對象,基于擬非線性摩擦模型與斯特里貝克效應,建立了機械臂關節非線性摩擦模型,研究了摩擦模型對末端運行軌跡的影響,結果表明:在關節角速度較低時摩擦對末端軌跡的非線性影響較大,反之影響較小;關節2對末端軌跡影響較小;關節3和4對機械臂末端軌跡影響較大。杜志江等[11]以某機械臂的高速軸與低速軸為研究對象,提出一種同時考慮摩擦、間隙和遲滯的綜合建模方法,并將所建立的模型在MATLAB/Simulink中進行了驗證,結果表明所建立的模型可以有效仿真出實際關節的各種非線性特性。劉才山等[12]針對重力場下作大范圍回轉運動的柔性梁與一固定斜面發生斜碰撞的情況,基于假設模態法與剛柔耦合效應的多柔體系統動力學建模理論,提出了考慮摩擦作用的多柔體系統的點-面碰撞模型,為解決具有變拓撲結構的多體系統動力學問題奠定了理論基礎。劉福才等[13]以二自由度機械臂為研究對象,建立了考慮摩擦和不考慮摩擦情況下機械臂的動力學模型,并采用PD算法對兩種情況下的動力學模型進行仿真研究,結果表明:摩擦對控制機械部運動的驅動力以及軌跡追蹤精度所產生的影響與重力密切相關,與重力大小呈正相關。
傳統的多體系統動力學研究主要圍繞多剛體構件進行,但隨著現代機械化及工作精度要求的提高,考慮剛性運動及其運動變形之間的耦合作用的彈性動力學問題,已成為目前的研究熱點[14]。僅運用剛體動力學或彈性力學都無法準確描述構件的剛性運動及彈性變形之間的耦合作用[15],故運用剛柔耦合體進行動力學仿真更接近真實情況。
本文作者采用虛擬樣機軟件ADAMS和有限元分析軟件ANSYS聯合建立一種六自由度串聯機械臂的剛柔耦合模型,并進一步考慮關節摩擦,對機器人進行動力學仿真,從而分析了單關節摩擦與多關節摩擦對機器人末端抖動的影響,為研究機器人的振動特性和設計改進提供了參考。
1 剛柔耦合振動模型的建立
基于ANSYS和ADAMS建立的剛柔耦合機械臂模型原理圖如圖1所示。用SolidWorks建立機構的實體模型,然后導入到ADAMS中;在ADAMS環境下給實體定義材料屬性、添加約束、施加驅動,在后處理過程中可列出各個構件所受的外加載荷、約束反力和慣性力;通過ANSYS對其進行受力分析以尋找薄弱環節,并將薄弱環節離散成小網格,然后進行模態計算;計算的模態中性文件以MNF(模態中性文件)形式重新導入ADAMS里替換剛性體,最終建立整個系統的剛柔耦合模型。

圖1 基于ANSYS和ADAMS建立的剛柔耦合機器人模型原理 圖2 剛柔耦合機器人模型
在進行六自由度串聯機器人振動規律的研究時,把與機器人末端抖動關系密切、變形較大的部件采取柔性化處理,即把機器人大臂、小臂及腰關節考慮為柔性體,其余變形量小且與機器人末端抖動聯系較少的部件仍處理為剛體。圖2所示為剛柔耦合機器人模型。
2 關節摩擦對機器人末端抖動的影響
2.1 單關節摩擦對機器人末端抖動的影響
圖3—圖8所示為各關節單獨存在摩擦時機械臂末端的加速度響應,從圖3中可以得出:當機器人各關節都不存在摩擦的理想狀態下,在機器人的整個運行工況中,其末端的抖動基本在±10 m/s2的范圍內波動,且波動的頻率相對較低。圖4所示為關節1存在摩擦時機器人末端抖動加速度響應情況,可知:在機器人運行0~1 s內其末端抖動最為劇烈,在±10 m/s2范圍內波動,1 s后,機器人末端抖動加速度響應明顯降低,并在后續運動過程中趨于平緩。圖5所示為關節二存在摩擦時機器人末端抖動加速度響應,可知:當機器人關節2存在摩擦時,機器人末端抖動頻率高,且抖動幅值大,在0~1 s其末端抖動在±125 m/s2范圍內波動,1~4 s內機器人末端抖動幅值顯著增加,且在-335~475 m/s2范圍內波動,4 s后,機器人末端抖動幅值突然減小,且趨于平緩,其抖動幅值在±168 m/s2范圍內變化。圖6所示為關節3存在摩擦時機器人末端抖動加速度響應情況,可知:機器人在0~1.17 s內末端抖動劇烈,抖動頻率高,且在0.49 s時其末端抖動幅值最大,為506 m/s2(圖中未示出);在0.49 s之后,末端抖動逐漸減小,且在1.17 s后在0上下小范圍波動,此時機器人末端抖動基本可以忽略不計。圖7所示為關節4存在摩擦時機器人末端抖動加速度響應情況,可知:關節4對機器人末端抖動的影響較小,0~1 s內抖動幅值在-6~9 m/s2范圍內變化,1 s后機器人末端抖動幅值減小,且抖動頻率也較小,在±2.5 m/s2范圍內變化。圖8所示為關節5存在摩擦時機器人末端抖動加速度響應情況,可知:機器人末端抖動幅值基本穩定在±6 m/s2范圍內變化,且波動頻率較低。

圖3 無關節摩擦時機器人末端抖動情況

圖4 關節1存在摩擦時機器人末端抖動情況
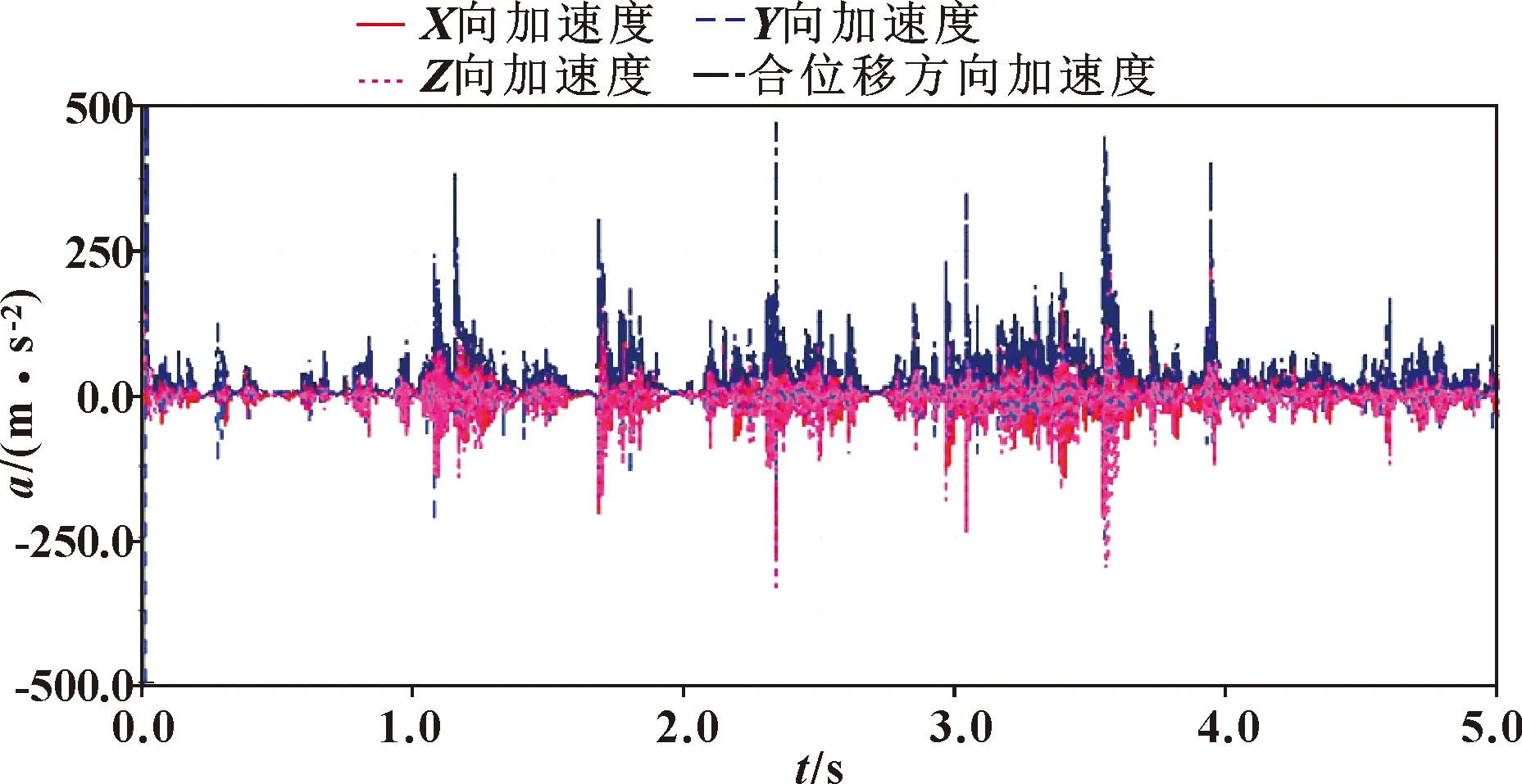
圖5 關節2存在摩擦時機器人末端抖動情況

圖6 關節3存在摩擦時機器人末端抖動情況
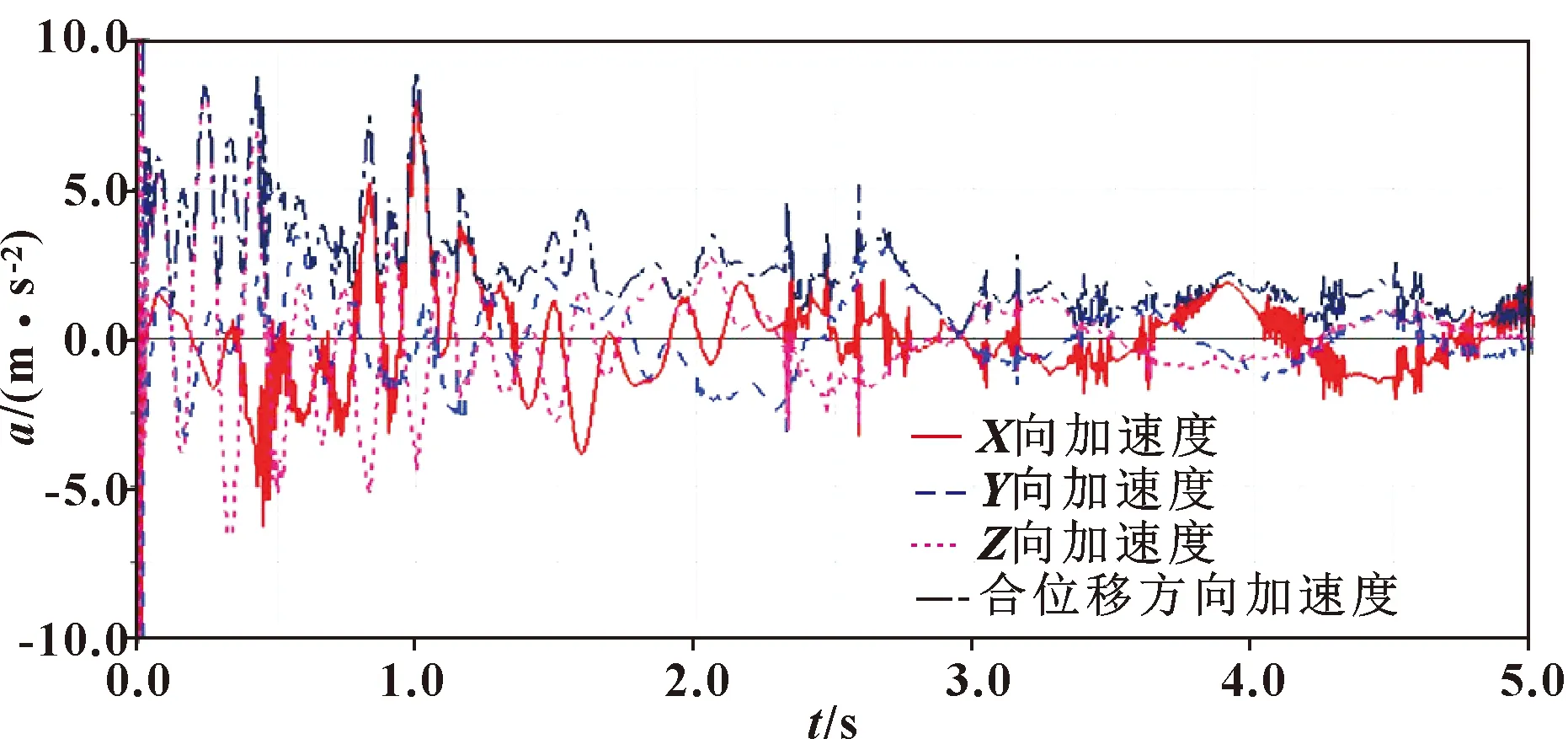
圖7 關節4存在摩擦時機器人末端抖動情況

圖8 關節5存在摩擦時機器人末端抖動情況
綜上所述:機器人關節1、關節4、關節5存在關節摩擦時,對機器人末端抖動幅值的影響較小;而關節2、關節3存在關節摩擦時,機器人末端抖動幅值發生劇烈變化,且抖動頻率也會顯著增加。機器人運動過程中,關節摩擦無法避免,其對機構的運動有顯著的影響。關節摩擦不僅會造成能量損耗,同時也會對機器人的動力學特性造成影響。由于關節2與關節3對機器人末端抖動影響較大,故將進一步考慮兩個關節摩擦同時存在的情況下,機器人末端的抖動情況。
2.2 多關節摩擦對機器人末端抖動的影響
圖9所示為所有關節同時存在摩擦時機器人末端抖動加速度響應情況,可知:在0~1.57 s時段內,機器人末端抖動幅值小;在1.57 s之后,機器人末端抖動劇烈,抖動幅值整體在-1 200~1 790 m/s2內變化。結合圖3可得:所有關節同時存在摩擦,會加劇機器人末端抖動。

圖9 所有關節存在摩擦時機器人末端抖動情況
圖10所示為關節2與關節3同時存在摩擦時機器人末端抖動加速度響應情況,2.096 5~2.2 s時段內機器人抖動最劇烈,抖動范圍為-560~900 m/s2;其次為3.3~3.7 s時段,抖動范圍為-336~650 m/s2;而在其余時段,機器人末端抖動幅值趨于平穩,基本在±50 m/s2附近變化。結合圖5、圖6可知:當關節2與關節3同時存在摩擦時,機器人末端抖動幅值明顯減小。主要是由于關節摩擦的存在造成了系統的能量損耗,從而造成了機器人加速度幅值的減小。

圖10 關節2和關節3存在摩擦時機器人末端抖動情況
3 摩擦因數大小對機器人末端抖動的影響
為進一步研究關節2與關節3的摩擦力大小對機器人末端抖動的影響,設置摩擦因數分別為0.07、0.1、0.13,其他參數值相同的情況下,對剛柔耦合機械臂系統進行動力學仿真分析。
3.1 關節2摩擦因數大小對機器人末端抖動的影響
圖11—圖13分別為關節2摩擦因數為0.07、0.1、0.13時機器人末端抖動情況。由圖11可知:當摩擦因數為0.07時,機器人末端抖動加速度幅值最大為1 723 m/s2,工作時段基本在±540 m/s2附近波動。由圖12可知:當摩擦因數為0.1時,機器人末端抖動加速度幅值最大為470 m/s2,且整體抖動相對平穩,基本保持在±350 m/s2內變化。由圖13可知:當摩擦因數為0.13時,機器人末端抖動加速度幅值最大為574 m/s2(圖中未示出),整體抖動范圍為±392 m/s2。綜上分析,當關節2摩擦因數為0.1時機器人末端抖動表現最弱。

圖11 關節2摩擦因數為0.07時機器人末端抖動情況
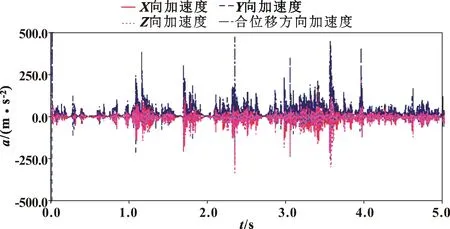
圖12 關節2摩擦因數為0.1時機器人末端抖動情況

圖13 關節2摩擦因數為0.13時機器人末端抖動情況
3.2 關節3摩擦因數大小對機器人末端抖動的影響
圖14—圖16分別為關節3摩擦因數為0.07、0.1、0.13時機器人末端抖動情況。可得:摩擦因數的改變,只引起了0.99~1.18 s時段內機器人末端抖動幅值的極小變化。故可得出機器人關節3摩擦因數的改變幾乎不會引起機器人末端抖動幅值的改變。

圖14 關節3摩擦因數為0.07時機器人末端抖動情況
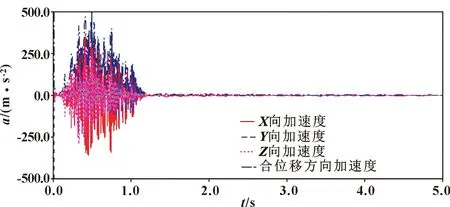
圖15 關節3摩擦因數為0.1時機器人末端抖動情況
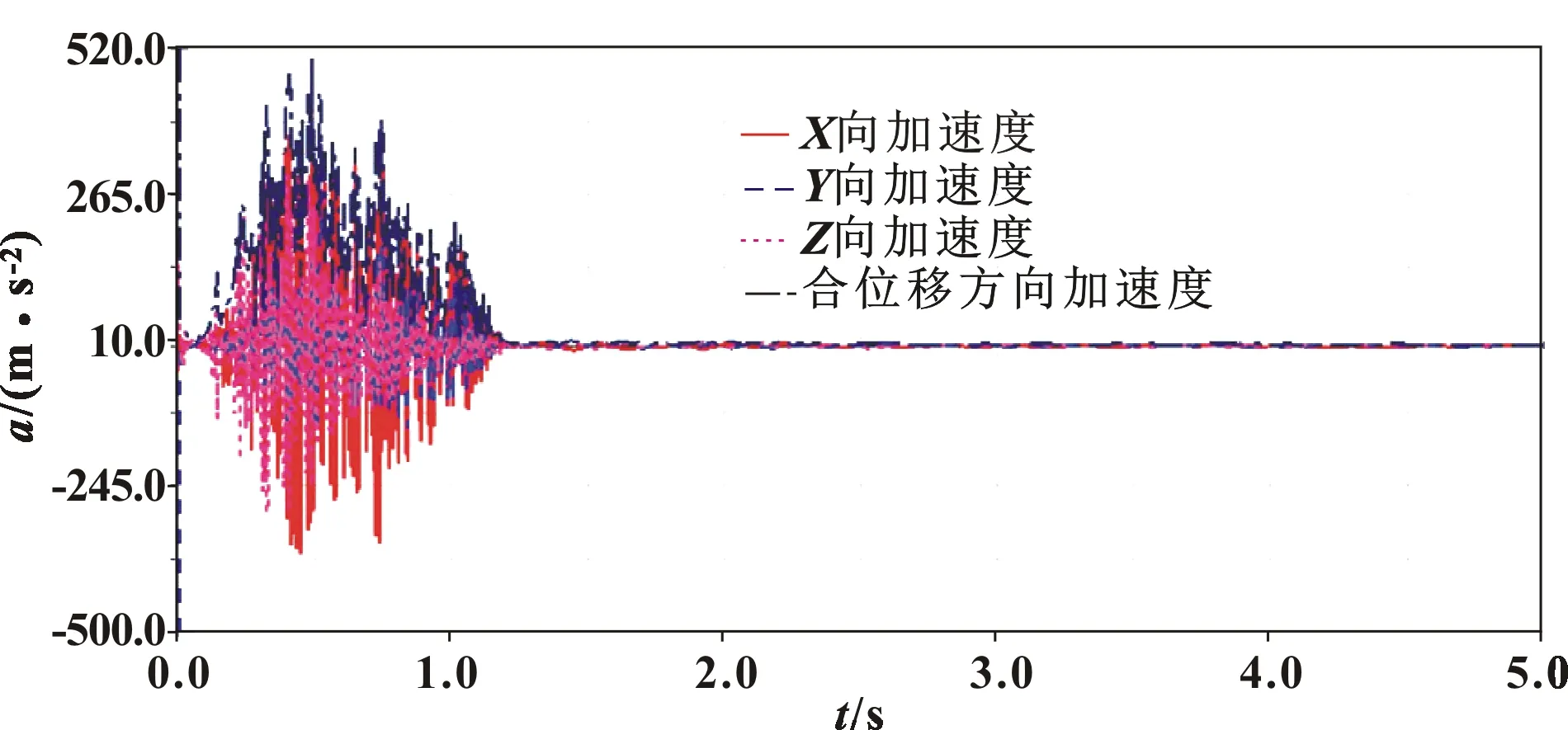
圖16 關節3摩擦因數為0.13時機器人末端抖動情況
4 結論
利用ADAMS和ANSYS聯合仿真建立六自由度機械臂的剛柔耦合模型,對其進行動力學仿真,分析單關節摩擦與多關節摩擦對機器人末端抖動的影響,得出以下結論:
(1)該六自由度串聯機械臂實際工作過程中,關節2、關節3存在摩擦時對機器人末端抖動的影響最顯著。
(2)機器人所有關節同時存在摩擦時,會加劇機器人末端抖動情況。但當只有關節2和關節3同時存在摩擦時,機器人末端抖動情況得到明顯改善,抖動劇烈時段大大縮短,抖動幅值也明顯降低。
(3)隨著摩擦因數的增大,機器人末端抖動幅值隨之減小,但機器人末端抖動幅值不會隨著摩擦因數的增大而無限度減小,摩擦因數只有在一定的范圍內進行取值,機器人末端抖動才會得到有效改善。關節2摩擦因數為0.1時機器人末端抖動表現最弱。但關節3摩擦因數的改變幾乎不會引起機器人末端抖動情況的變化。

