基于壓痕應變的不銹鋼材料拉伸性能參數計算方法

薛 河，路景智，賈宇磊，王 雙，王 正

(西安科技大學機械工程學院，西安 710054)

0 引 言

工程結構中的許多部件都是通過焊接技術連接起來的，如核電壓力容器及管道等；焊接工藝的特點使得焊接接頭成為工程結構的薄弱區域[1]，并且焊接接頭區域的力學性能會呈現出不均勻的特點[2]，這就對局部材料力學性能的獲取提出了更高的要求。通過傳統力學試驗獲取材料力學性能時，需要在待測部位進行破壞性取樣，且取樣區域較大，難以對焊接接頭局部不同區域的力學性能進行準確分析[3]。微納米壓痕試驗作為一種無需取樣的技術，因具有操作簡單、執行速度快、破壞性小等優勢，已逐步成為測試在役設備材料力學性能的重要方法[4-5]。

微納米壓痕試驗起源于材料的硬度試驗[6]，經發展和改進后被用于測試材料的硬度與彈性模量[7-8]。20世紀80年代初，HAGGAG等[9-10]提出了在被測材料同一點處進行多次加卸載循環的自動化連續球壓痕(ABI)測試技術。近年來，連續球壓痕測試技術被廣泛用于測試金屬材料的力學性能[11-13]。有學者通過連續球壓痕試驗測試了壓力容器用鋼的拉伸性能參數，并通過與拉伸試驗結果進行對比驗證了該方法的可行性與準確性[14-16]。關凱書等[17]通過引入損傷理論獲得了連續球壓痕試驗的塑性表征參數。瞿力錚等[18]采用三維建模方法對典型冪硬化金屬的連續球壓痕試驗進行模擬，并對影響拉伸性能計算結果的因素進行了分析。此外，XUE等[19]采用連續球壓痕試驗結合有限元反演分析，開發了一種獲得不銹鋼材料在不同伸長率下應力-應變關系的方法。目前，連續球壓痕測試技術主要通過擬合無量綱方程來計算材料拉伸性能參數，但由于加卸載過程中材料凹陷/凸起對壓痕響應參數的影響，計算誤差較大。

為了建立更為準確的材料拉伸性能參數計算方法，作者利用ABAQUS軟件建立三維有限元模型模擬連續球壓痕試驗過程，通過單一變量模擬分別建立彈性模量、屈服強度、應變硬化指數與殘余壓痕應變的關系；在125組不銹鋼拉伸性能參數組合下對連續球壓痕試驗進行有限元模擬，建立了基于殘余壓痕應變的不銹鋼材料拉伸性能參數計算方法。

1 連續球壓痕應變測試原理

在平面應力場中，當壓頭壓入被測材料時材料因受力而發生變形，由這種變形行為產生的應變變化被稱為壓痕應變增量。當被測材料的力學性能發生變化時，壓頭壓入產生的壓痕應變增量也會具有不同的變化規律。因此，可以利用壓痕誘導產生的壓痕應變增量對材料拉伸性能參數進行求解。如圖1所示，將電阻應變片粘貼于試樣表面，在應變柵軸線中心處控制壓頭沿垂直于試樣表面方向以一定的速率進行加卸載，每次加卸載構成一個循環；在每次加卸載循環過程中，通過位移傳感器與應變記錄儀實時記錄不同壓入深度下的壓痕應變增量。建立連續球壓痕試驗有限元模型，模擬得到壓痕應變增量與材料拉伸性能參數之間的對應關系，借助有限元反演分析將壓痕應變增量轉化為材料的拉伸性能參數。

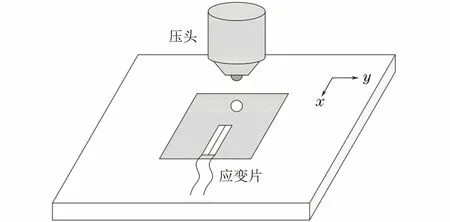
圖1 壓痕應變測試示意Fig.1 Diagram of indentation strain measurement

對于大多數不銹鋼材料而言，其彈塑性行為可以用冪律方程近似描述為

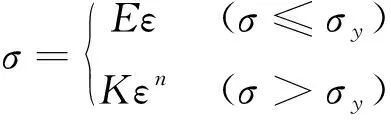
(1)

式中：σ為應力；E為彈性模量；K為強化系數；n為應變硬化指數；σy為屈服強度；ε為總應變。

當σ>σy時，式(1)可改寫為

(2)

式中：εp為超過屈服階段后不可恢復的塑性應變。

2 有限元模擬

采用ABAQUS軟件建立三維有限元模型模擬連續球壓痕應變測試過程，由于試樣結構及所受載荷具有對稱性，故建立1/4模型。考慮到應變測試的準確性，模型中試樣尺寸設為10 mm×10 mm×3 mm，球形壓頭的直徑為1 mm。壓頭材料為碳化鎢，其彈性模量遠大于被測材料，在壓入過程中不會發生變形，因此將其設置為剛體。

在壓入過程中，試樣的變形主要發生在與壓頭接觸的區域，而在遠離壓頭的區域卻幾乎沒有變形。采用C3D8R網格單元進行網格劃分，對靠近壓頭部位的網格進行細化，如圖2所示，最小網格尺寸為0.025 mm，從而保證壓痕應變測試局部區域的響應精度。對于非接觸區域，網格單元尺寸隨距壓頭距離的增加逐漸增大。

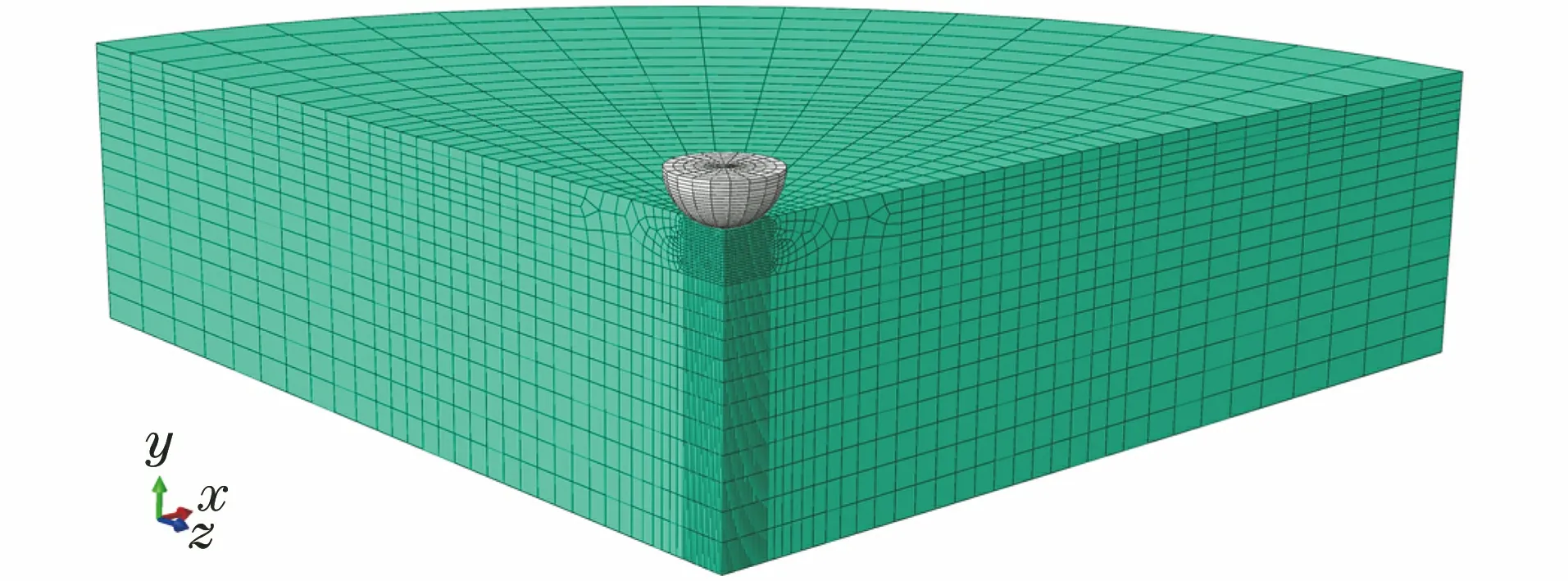
圖2 有限元模型及網格劃分Fig.2 Finite element model and mesh generation

邊界條件設置為試樣底面完全固定，在對稱面上施加對稱性約束；對壓頭參考點施加位移載荷，使壓頭只能沿垂直于試樣表面的方向進行移動。設置5次加卸載循環，第一次循環時壓入深度h為0.10 mm，第2次為0.15 mm，直至最大壓入深度為0.30 mm，加載過程為準靜態過程。材料模型選擇Hollomon冪硬化本構模型，遵循Von Mises屈服準則。

金屬材料具有彈塑性特性，在壓頭卸載之后會發生一定程度的彈性恢復。設置了單一變量試驗組，具體不銹鋼材料拉伸性能參數如表1所示。參考GB/T 24179-2009，選擇距壓痕中心3 mm處作為殘余壓痕應變的測試點，采用有限元模型模擬加卸載過程，得到每次加卸載循環后測試點處的殘余壓痕應變，分析殘余壓痕應變的變化規律。

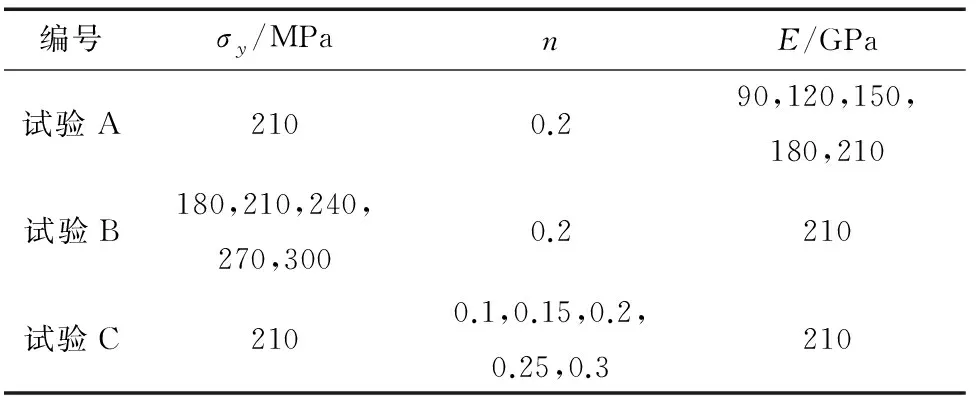
表1 有限元模擬用不銹鋼材料拉伸性能參數

3 基于殘余壓痕應變的材料拉伸性能參數計算方法

3.1 彈性模量與殘余壓痕應變的關系

由圖3可以看出：當屈服強度與應變硬化指數為定值時，相同壓入深度下，彈性模量越大，殘余壓痕應變越小，彈性恢復能力越強；殘余壓痕應變與彈性模量的對數之間存在良好的線性關系，其線性擬合相關系數R2為0.999，擬合公式為

lnεr=a1lnE+a0

(3)

式中：εr為殘余壓痕應變；a0，a1為擬合系數。

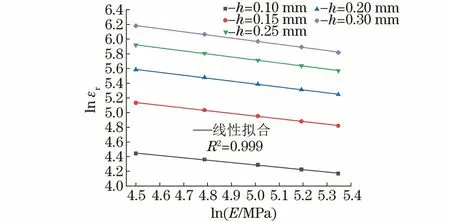
圖3 有限元模擬得到不同壓入深度下殘余壓痕應變和彈性模量的對數關系Fig.3 Logarithmic relationship between residual indentation strain and elastic modulus at different indentation depths by finite element simulation

3.2 屈服強度與殘余壓痕應變的關系

由圖4可以看出：當彈性模量與應變硬化指數為定值時，相同壓入深度下，隨屈服強度增加，殘余壓痕應變增大，說明材料發生變形后保留塑性變形的能力增強；不同壓入深度下屈服強度與殘余壓痕應變的對數同樣具有明顯的線性關系，線性擬合相關系數為0.999，擬合公式為

lnεr=b1lnσy+b0

(4)

式中：b0，b1為擬合系數。

圖4 有限元模擬得到不同壓入深度下殘余壓痕應變和屈服強度的對數關系Fig.4 Logarithmic relationship between residual indentation strain and yield stress at different indentation depths by finite element simulation

3.3 應變硬化指數與殘余壓痕應變的關系

由圖5可以看出：當彈性模量與屈服強度為定值時，相同壓入深度下，應變硬化指數越大，殘余壓痕應變越大；不同壓入深度下殘余壓痕應變的對數與應變硬化指數呈冪律關系，擬合相關系數為0.999，擬合公式如下：

lnεr=c2n2+c1n+c0

(5)

式中：c0，c1，c2為擬合系數。

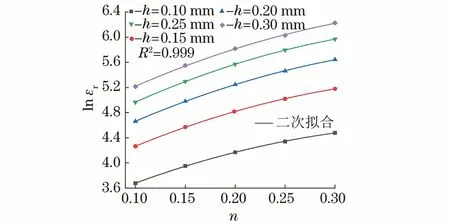
圖5 有限元模擬得到不同壓入深度下殘余壓痕應變對數和應變硬化指數的關系Fig.5 Relationship between logarithmic residual indentation strain and strain hardening exponent at different indentation depths by finite element simulation

3.4 材料拉伸性能參數計算方法的建立

結合式(3)～式(5)，即可建立殘余壓痕應變與彈性模量、屈服強度和應變硬化指數的關系式：

lnεr=alnE+blnσy+cn2+dn+e

(6)

式中：a，b，c，d，e為擬合系數。

在試驗參數范圍，即彈性模量90～210 GPa、屈服強度180～300 MPa、應變硬化指數0.1～0.3范圍內，共有125種不同拉伸性能參數組合。在每組拉伸性能參數下進行5次加卸載連續球壓痕試驗的有限元模擬，得到不同壓入深度下的殘余壓痕應變。采用式(6)對材料拉伸性能參數和不同壓入深度下的殘余壓痕應變進行擬合，得到不同壓入深度下的擬合系數，如表2所示；將這些系數代入式(6)，再代入由連續球壓痕試驗測定的材料殘余壓痕應變，即可反演計算得到材料的拉伸性能參數。

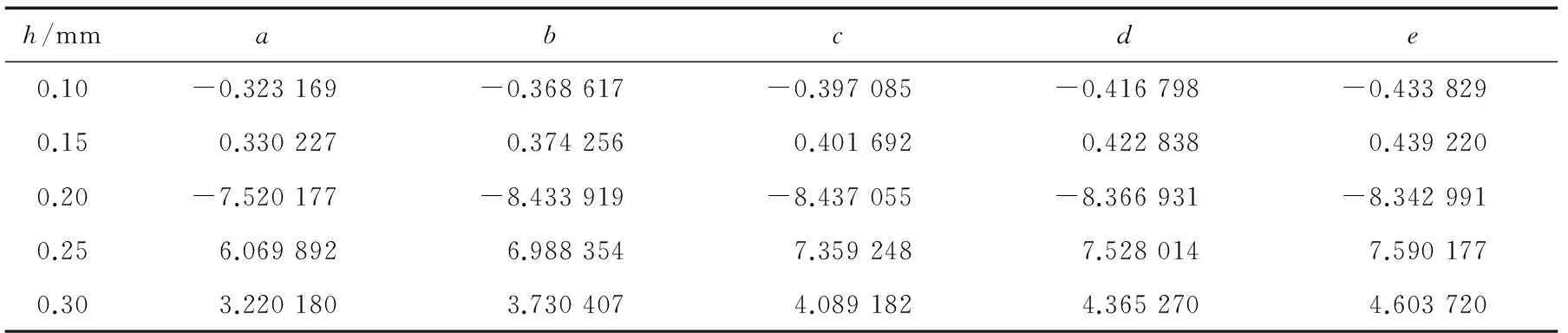
表2 不同壓入深度下的擬合系數

4 試驗驗證

以山西太鋼不銹鋼有限公司提供的316L不銹鋼薄板為研究對象。按照GB/T 4340.1-1999，在卷板機上將316L不銹鋼薄板軋制成2 mm厚的薄板試樣，再利用線切割法加工成板狀拉伸試樣，尺寸如圖6所示。利用PLD-50型疲勞拉伸試驗機進行單軸拉伸試驗，拉伸速度為2 mm·min-1，進行3次重復試驗，取3次試驗結果的平均值作為材料拉伸性能參數。試驗測得316L不銹鋼的彈性模量為205.2 GPa，屈服強度為248.8 MPa，應變硬化指數為0.136 0。

圖6 板狀拉伸試樣尺寸Fig.6 Dimension of plate-shaped tensile sample

為避免試樣翹曲對試驗結果造成影響，截取板狀拉伸試樣的標距段，鑲嵌后進行表面拋光處理，直至試樣表面沒有明顯劃痕，在其表面粘貼BX120-3AA型應變片。將粘貼有應變片的試樣放置在剛性支座上，確保試驗載荷垂直于試樣表面，在改造的UTM2000型電子萬能試驗機上進行連續球壓痕試驗，壓入過程采用位移控制，下壓速度為0.1 mm·min-1，共進行5次加卸載過程，卸載率為50%，整個加載過程為準靜態，每次加卸載循環時的壓入深度與有限元模擬時一致，即第一次循環時壓入深度為0.10 mm，第2次為0.15 mm，直至最大壓入深度為0.30 mm。利用DH3818Y型靜態應變測試儀實時監測試樣表面的應變，記錄不同壓入深度下壓痕產生前后的應變差值(即殘余壓痕應變)，共進行3次連續球壓痕試驗取平均值。將不同壓入深度下的殘余壓痕應變代入式(6)，反演計算得到316L不銹鋼的拉伸性能參數并取平均值。由計算結果可知，316L不銹鋼的彈性模量為208.3 GPa，屈服強度為252.7 MPa，應變硬化指數為0.135 7，與拉伸試驗結果的相對誤差分別為1.50%，1.57%，0.22%。相對誤差均保持在2%以內，說明基于殘余壓痕應變的不銹鋼材料拉伸性能參數計算方法可以滿足工程需要。

5 結 論

(1) 建立連續球壓痕試驗三維有限元模型，通過單一變量法模擬得到不銹鋼材料殘余壓痕應變隨彈性模量增加而降低，隨屈服強度或應變硬化指數的增大而提高；殘余壓痕應變分別與彈性模量和屈服強度存在對數線性關系，殘余壓痕應變對數與應變硬化指數之間存在冪律關系。

(2) 根據由單一變量法得到的各關系式，建立不銹鋼材料的殘余壓痕應變與彈性模量、屈服強度和應變硬化指數關系式，在125組不同不銹鋼材料拉伸性能參數下進行連續球壓痕試驗有限元模擬，擬合得到基于殘余壓痕應變的不銹鋼材料拉伸性能參數計算公式。通過連續球壓痕試驗測定得到316L不銹鋼的殘余壓痕應變，再反演計算得到的彈性模量、屈服強度、應變硬化指數與拉伸試驗結果的相對誤差分別為1.50%，1.57%，0.22%，相對誤差均保持在2%以內，說明基于殘余壓痕應變的材料拉伸性能參數計算方法可以滿足工程需要。