廣義河床流體模型方程單調遞減扭狀孤波解的漸近穩定性

張 坤， 汪成偉， 張衛國

（上海理工大學 理學院，上海 200093）

1 問題的提出

廣義河床流體模型方程

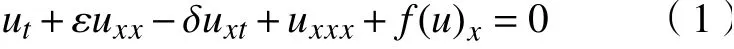
是一個重要的模型方程，其中，δ ≥0，f(u)=βup+1，p為任意的正整數，常數 β ＞0。 不難發現，當p=1時，式(1)即化為河床流體模型方程

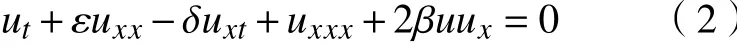
方程(2) 源自于兩相流體模型的研究[1-5]。當ε=δ=0，p=1時，方程(1)即化為KdV 方程[6]

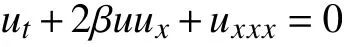
當 δ =0，p=1時，方程(1)可以化為KdV-Burgers方程[7-12]

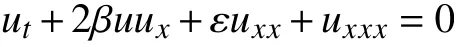
當 δ =0，p=2時，方程(1)可以化為MKdV-Burgers方程[13-16]

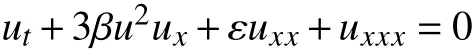
文獻[3-5]用數值分析法研究了方程(2)在條件

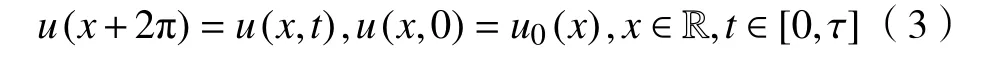
下的周期初邊值問題，文獻[3-4]的研究證明，對周期初邊值問題(2)和(3)采用通常的差分方法及Galerkin 有限元法得到的差分格式是不穩定的。為此，文獻[4]利用特殊技巧給出了其在空間方向上的一個半離散穩定的差分格式。文獻[5]用穩定化有限元法的思想，對問題(2)和(3)在一定條件下給出了一種全離散的穩定的差分格式，并用能量法證明了該差分格式的非線性穩定性及收斂性。

若 耗 散 系 數 ε,δ 滿 足 ε+cδ ＜-λ0(ε+cδ ＞λ0)，則方程(2)有唯一的單調遞減(遞增)扭狀孤波解；

若耗散系數 ε ,δ 滿足- λ0＜ε+cδ＜0(0＜ε+cδ＜λ0)，則方程(2)有唯一的衰減振蕩解。

文獻[17] 求出了在耗散作用較小(即|ε+cδ|＜λ0)時，方程(2)衰減振蕩解的近似解，且給出了近似解與真解的誤差估計。但文獻[17]并沒有研究當 ε+cδ ＜-λ0時方程(2)單調遞減扭狀孤波解的穩定性。

受文獻[17]的啟發，本文將研究廣義河床流體 模 型 方 程(1) 在 耗 散 系 數 ε,δ滿 足ε+cδ ＜-λ?(λ?待求) 時，單調遞減行波解u(ξ)的存在性，以及其是否具有漸近穩定性的問題。

2 方程(1) 單調遞減扭狀孤波解的存在性

運用平面動力系統的理論[19-21]來研究方程(1)在ε+cδ ＜-λ?情況下單調遞減行波解的存在性。

設方程(1) 具有行波解u(t,x)=u(ξ)=u(x-ct)，則u(ξ)滿足

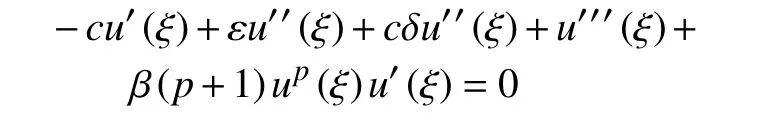
其中，c為波速。對上式關于 ξ積分一次，可得

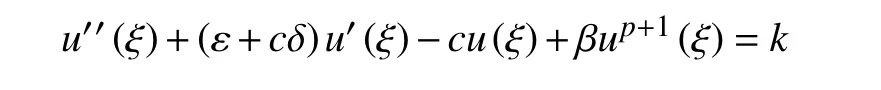
這里的k是積分常數。由于本文主要研究的是系統的耗散效應，假設所研究的行波解滿足

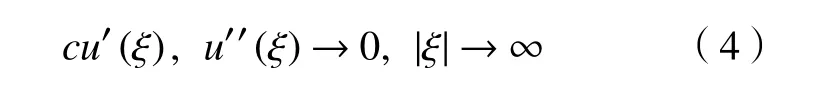
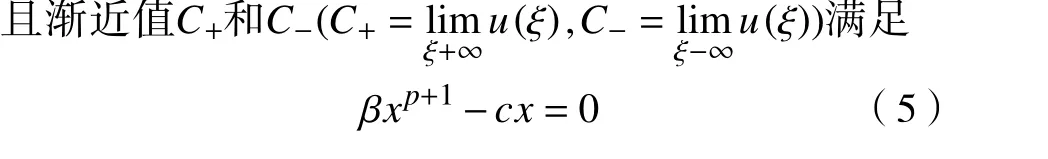
由此，在假設式 (4) 和 式 (5)條件下，方程(1) 的行波解滿足

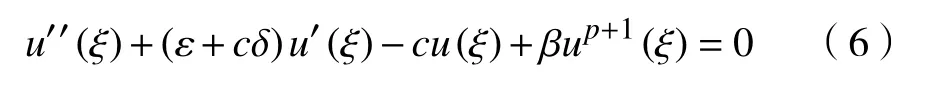
在接下來的討論中，始終假設方程(1)的行波解滿足式(4)和式(5)。

令x=u(ξ)，y=u′(ξ)，則方程(6)等價于如下平面動力系統:

由于方程(6)的有界解對應于系統(7)的有界軌線。 因此，可以通過研究系統(7)的有界軌線及其性態來研究方程(6)的解及性態。

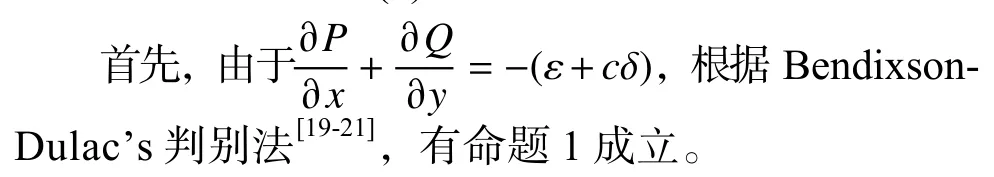
命題1 當 ε+cδ ≠0時 ，系統(7) 在 (x,y)平面上不存在閉軌線和具有有限個奇點的奇異閉軌線。進而當 ε+cδ ≠0時，方程(1)不存在周期波解和鐘狀孤波解。

在平面 (x,y)上，系統(7)的有限遠奇點的個數依賴于代數方程f(x)=βxp+1-cx=0 。 記x0=0，x1=(c/β)1/p，x2=-x1。 對于f(x)=0的實根，有以下結果：

a. 若c＞0， 當p為 偶數時，方程f(x)有3 個不同 的 實 根x0，x1，x2； 當p為 奇 數 時，方 程f(x)有2 個不同的實根x0，x1。

b. 若c＜0， 當p為 偶數時，方程f(x)僅有1 個實根x0； 當p為 奇數時，方程f(x)有2 個不同的實根x0，x1。

由于系統(7) 在c＜0且p為偶數時只有1 個奇點，故在 ε+cδ ≠0情況下方程(1)不存在有界行波解，所以，將不考慮這種情況。

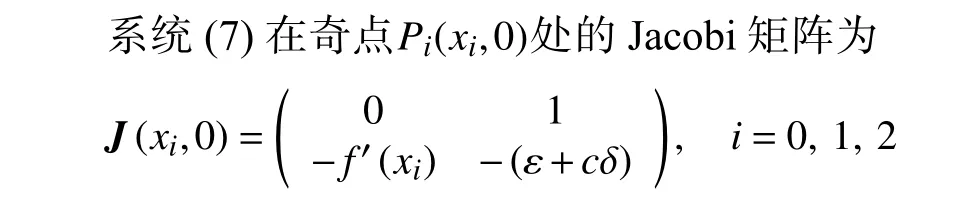
因 此，J(xi,0)的 行 列 式 即 det(J(xi,0))等 于f′(xi)，i=0, 1, 2。 用 Δi表 示特征方 程在Pi(xi,0)處 的判別式，Δi=(ε+cδ)2-4f′(xi)，i=0, 1, 2。 從而可知Δ0=(ε+cδ)2+4c，Δ1=(ε+cδ)2-4pc； 如 果p為 偶 數，則有 Δ1=Δ2。

接下來運用平面動力系統的理論和方法[19-21]討論系統(7) 奇點的類型，并給出在條件ε+cδ ＜0下的全局相圖。

在條件ε +cδ ＜0 下 ，由于d et(J(0,0))=f′(0)=-c，易 知 當c＞0時 ，P0為 鞍 點；當c＜0且 Δ0＞0時，P0為 不穩定的結點；當c＜0且 Δ0＜0時 ，P0為不穩定的焦點。奇點Pi的類型如下所示：

a. 若c＞0， 當p為 偶數時，由于det(J(xi,0))=f′(xi)＞0 ， 當 Δ1＞0時 ，Pi(i=1,2)為 不 穩 定 的 結點；當 Δ1＜0時 ，Pi(i=1,2)為不穩定的焦點。當p為奇數時，由于 det(J(x1,0))=f′(x1)＞0， 當Δ1＞0時 ，P1為 不穩定的結點；當 Δ1＜0時 ，P1為不穩定的焦點。

b. 若c＜0， 當p為奇數時，系統(7)有2 個奇點P0(0,0)和P1(x1,0)。 又 因 為det(J(x1,0))=f′(x1)＜0， 故P1為鞍點。

用Poincare 變換對系統(7) 作無窮遠奇點分析，易知在y軸的正負2 個方向上有一對無窮遠奇點A1和A2。 其 中，A1位 于y軸 的 正 半 軸，A2位于y軸的負半軸。當p為偶數時，點Ai(i=1, 2)周圍存在1 個雙曲型區域；當p為奇數時，點Ai(i=1, 2)周圍存在1 個拋物型區域。此外，Poincare 圓盤的圓周為軌線。

根據上述定性分析，可以得到系統(7) 在ε+cδ ＜0條件下的全局相圖，如圖1 所示。

由圖1 可以得到命題2。

命題2 設 ε +cδ ＜0。 若c＞0，p為偶數，系統(7)存在2 個異宿軌線L(P1,P0)和L(P2,P0)(圖1(a)和(b))；當p為 奇 數 時，無 論c＞0或c＜0，系統(7) 均 存 在1 個 異 宿 軌 線L(P1,P0)或L(P0,P1)(圖1(c)～(f))。

由于平面動力系統中的同宿軌和閉軌對應于相應非線性發展方程的鐘狀孤波解和周期波解，異宿軌對應于扭狀孤波解或振蕩行波解等。因此，由命題2 和圖1 可以得到定理1 和定理2。

定理1 設 ε+cδ ＜0， 若c＞0，p為偶數，方程(1)有2 個有界行波解(對應于圖1(a)和(b)中的異宿軌線L(P1,P0)和L(P2,P0)) ；當p為奇數時，無論c＞0或c＜0，方程(1) 均有1 個有界行波解(對應于圖1(c) ～ (f)中的異宿軌線)。

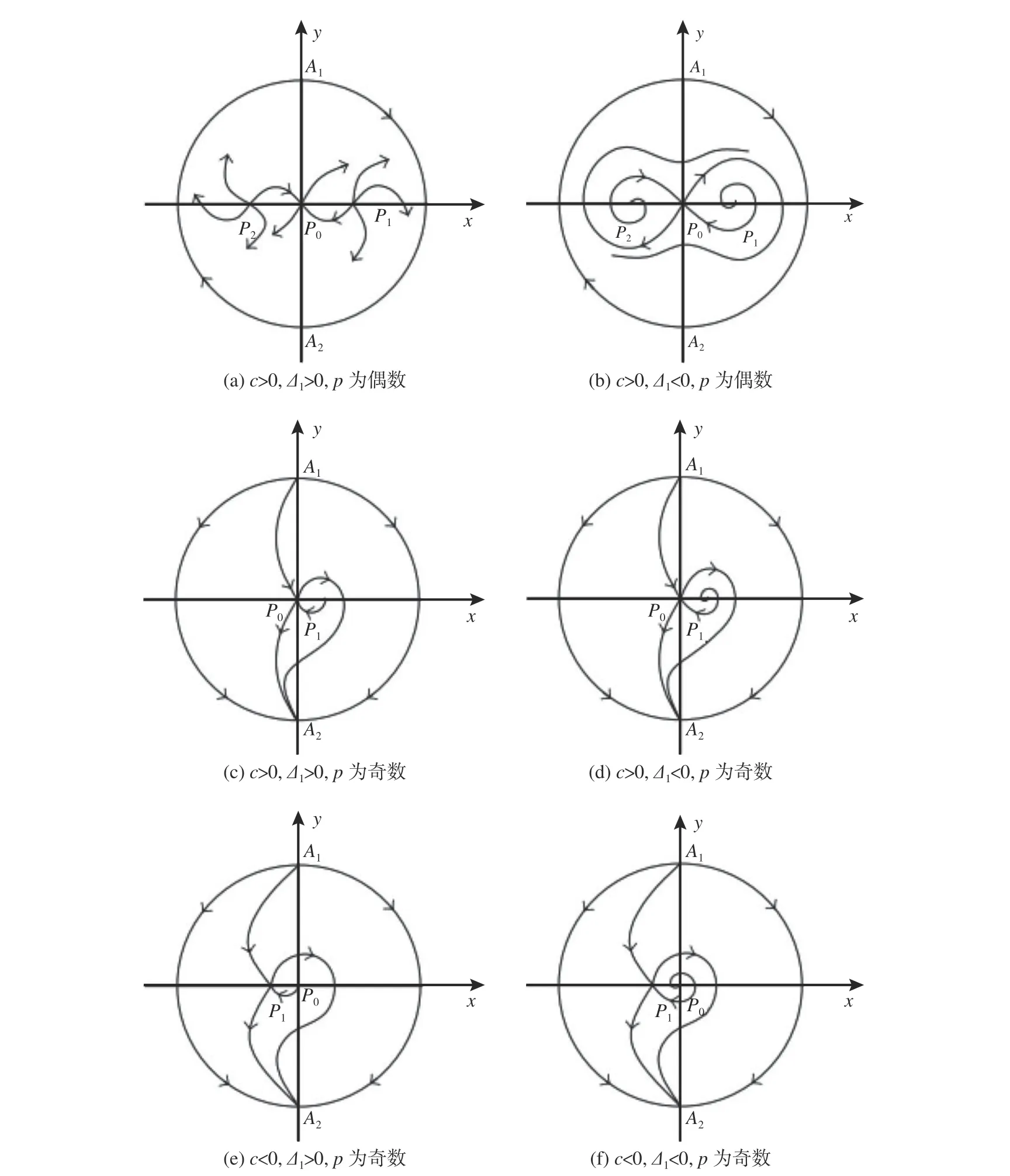
圖1 ε +cδ<0時的全局相圖Fig.1 Global phase diagrams when ε+cδ<0

現給出方程(1)的有界行波解受耗散作用影響的有關結論。

由于行波解u(ξ)在 沿x軸運動時其形狀與波速保持不變，不失一般性，假設 ξ ?1=0 或ξ1=0，則定理2 的結論b 所描述的振蕩行波解的性態如圖2所示。

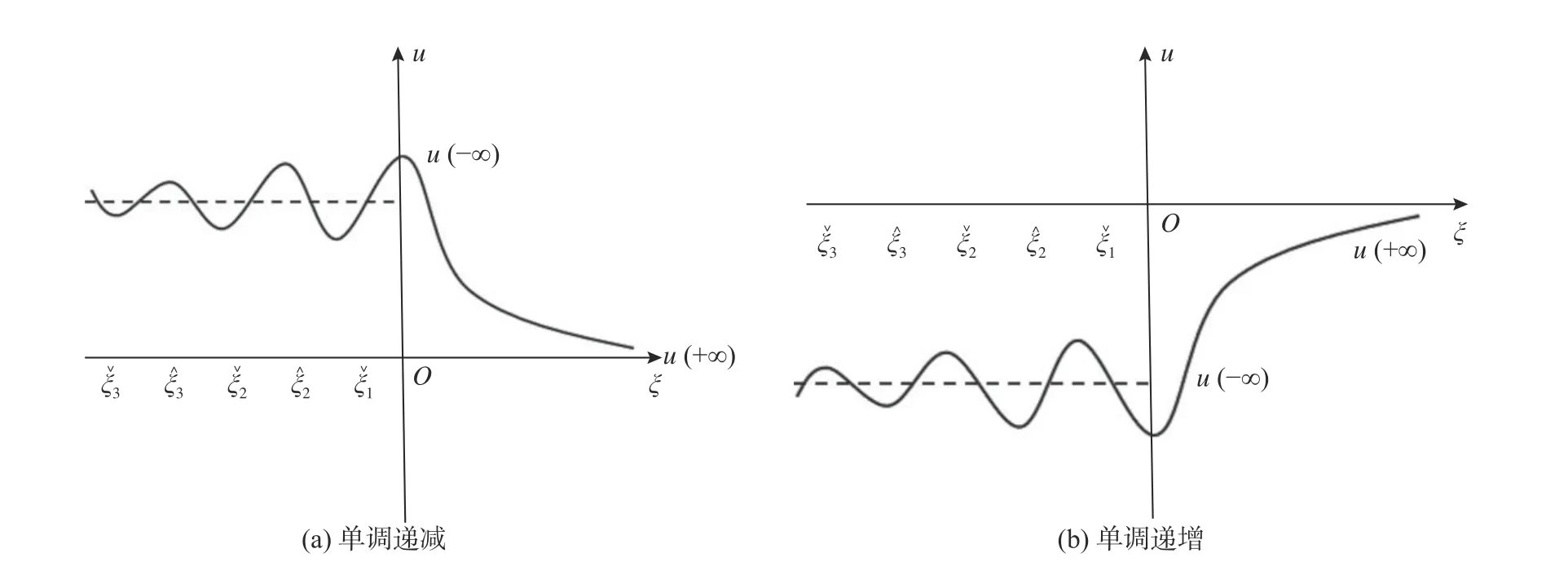
圖2 c >0,-2 <ε+cδ<0時的振蕩行波解示意圖Fig.2 Schematic diagramsofoscillatory travelingwavesolutionswhen c＞0,-2 <ε+cδ<0

3 廣義河床流體模型方程扭狀孤波解的重要性質

故存在常數C，使得

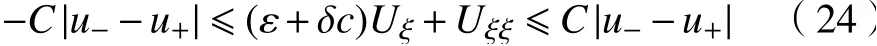
現將式(24)兩邊同乘 e(ε+δc)ξ，有

4 單調遞減扭狀孤波解漸近穩定性定理

考慮方程(1)的初值問題，初值條件為

將式(31)對 ξ進行積分，并令積分常數為0，則有

定理4 的證明可分成擾動方程初值問題(32)和問題(34) 解的整體存在性和漸近穩定性兩部分。先給出初值問題(32)和問題(34)解的整體存在性。

定理5 假設 Φ0∈H2， 則存在與u±無關的常數μ1,γ1(γ1≤γ0) 和 正 常 數C1， 使 得 當 |u--u+|≤μ1和N0=‖Φ0‖H2+‖Φ0ξ‖H1≤γ1，初 值 問 題(32) 和 問題(34)的解 Φ在X(0,∞)中是全局唯一存在的，且對任意的t∈[0,∞)滿足

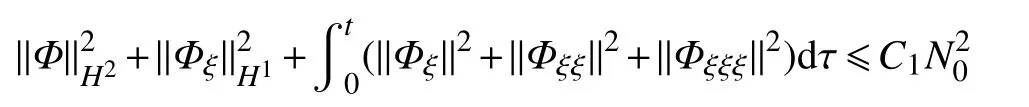
其中， Φξ由 式(31)定義， Φ0ξ為其初值。

為證明定理5，需要在局部解存在性的基礎上給出一致先驗估計。關于初值問題(32) 和問題(34)的解的局部存在性，有命題3。

命題3 (局部存在性) 假設N0≤γ0，則存在正常數T0(γ0)使 得問題(32) 和問題(34) 有唯一解Φ ∈X(0,T0)，且滿足

命題3 可以利用Galerkin 方法或不動點定理按標準方法進行證明(可參考文獻[25-26]等)。這里由于篇幅限制，省略證明過程。

在以下的推理過程中將用到2 個不等式，現以引理的形式給出。

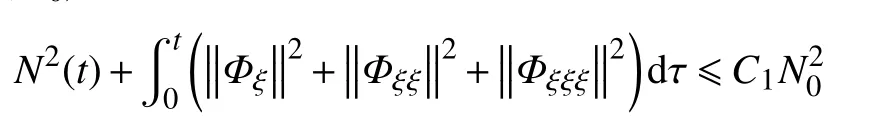
故式(37)可寫為

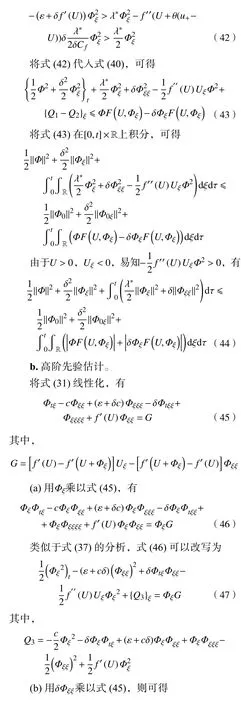
綜合不等式 (55)～(58)，對式(54)右端有下列估計：

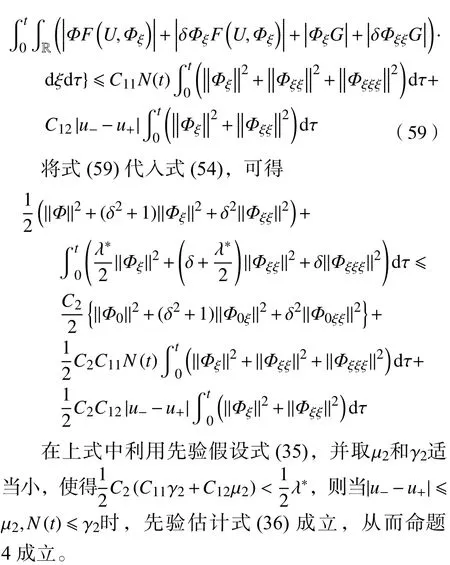
現在已經得到了初值問題(32) 和問題(34)的解的局部存在性和一致先驗估計。在此基礎上，通過連續性討論來證明定理5。

現給出定理4 的證明。

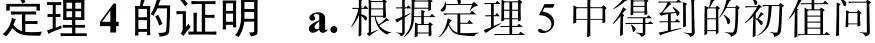
故定理4 得證。

通過以上對定理4 的證明，可得出廣義河床流體模型方程(1)的單調遞減扭狀孤波解具有漸近穩定性。