求解柔性流水車間調度問題的粒子群優化算法

范雅男，逄煥利

(長春工業大學 計算機科學與工程學院， 吉林 長春 130102)

0 引 言

車間調度問題[1](Job Shop scheduling， JSP)是對資源和時間路徑進行整合分配達到實際生產需求的過程。流水車間調度問題[2]是生產制造業中極其重要的規劃問題，一般該類問題的研究任務數都需要大于3，被證明是NP-hard問題。在智能生產制造業高速發展的背景下，車間的柔性生產越來越受到重視，柔性流水車間調度問題[3](Flexible Flow Shop scheduling Problem， FFSP)已成為實際生產調度問題研究領域的新熱點，對提高企業生產效率具有重要意義。

粒子群算法(Particle Swarm Optimization， PSO)[4-5]的突出優點在于容易實現，收斂效率較高，涉及到的可調整參數比較少。它可以利用實數進行編碼，算法結構不復雜的同時又適用于多個領域，既適合做理論研究，也能應用到具體的工程問題中。因此，PSO算法得到了各領域研究者的廣泛關注，在被提出后的短短幾年內便產生了許多科研成果，成為熱門的研究方向，并且被應用到許多工程領域。

目前對FFSP問題的研究主要集中在采用精確算法、元啟發式算法[6]、啟發式算法[7]方向上。如Ihong Kuo等[8]將全新的編碼方式和個體更新方案融入PSO算法中以求解FFSP問題。 Marichelvam M K等[9]對布谷鳥搜索算法進行優化，將改進的算法應用于HFSP問題的求解。田野等[10]將多種元啟發式方法混合后用于PFSP問題的求解。裴小兵等[11]提出的一種基于NEH的混合螢火蟲算法在解決含有多個目標的置換流水車間調度問題時效果良好。景會成等[12]針對搜索效率低、容易收斂于局部最優解等問題，采用模擬退火算法、粒子群算法、遺傳算法三種算法融合的方式對FSSP問題進行求解。

文中將禁忌策略和粒子群算法相結合形成一種新的優化算法，并將其應用于FFSP問題的求解。采用NEH算法產生初始種群，并引入非線性自適應慣性權重因子和擾動因子。最終通過仿真對比實驗的分析結果驗證了所提算法的有效性。

1 問題描述

柔性流水車間調度問題可以描述為：n個待加工工件Ji(i=1，2，…，n)在m臺機器Mk(k=1，2，…，m)上進行加工，每個工件包括一道或多道工序Oij(j=1，2，…，Pi)。任何工件的每次操作都必須遵循相同的機器順序。FFSP存在以下假設：開始時刻所有的機器都可以執行加工操作；各工件的每個操作可以在相應階段上選擇任意一臺并行處理機進行加工；工件中的任一操作每次只能在一臺機器上執行；每臺機器在任何作業上一次只能執行一次操作；機器上的操作一旦開始，就不得終止。文中涉及的模型參數見表1。

表1 模型參數表

問題目標是調配工件的加工處理順序以及機器調度方案，使得最大完成時間指標達到極小。因此該問題的數學公式描述如下：

minCmax=maxCmin;

(1)

Cijk=Sijk+tijk;

(2)

Sijk=max{S(i-1)(j-1)k+t(i-1)(j-1)k,Ci(j-1)(k-1)}；

(3)

Ck=Ci′j′k′。

(4)

式(1)為提出模型的目標函數；式(2)表示工件操作完成時間由開始處理時間和處理過程花費時間的總和；式(3)表示某工件上一個操作的完成時間，該機器上一次操作的處理完成時間決定了該工件開始處理的時間；式(4)表示某機器的處理完成時間為它上面最后一個操作的處理完工時間。

2 改進粒子群算法設計

2.1 編碼與解碼

采用基于工序和機器的編碼方式。假設一個3×3問題解決方案是{1，3，2，1，2，1，2，3，2，3，1，3，2，1，2，1}，前半部分用來判斷各工序的先后加工順序，后半部分用來選擇各工件操作的加工機器。{1，3，2，1，2，1，2，3}為工序調度，其中最前面的 “1”代表工件1的第一道工序O11，第二個“1”代表工件1的第二道工序O12，依此類推。{2，3，1，3，2，1，2，1}為機器分配部分與工序調度相匹配，其中“2”代表操作O11被分配到機器2上進行處理，“3”代表操作O31被分配到機器3上進行處理，依此類推。解碼為編碼的逆過程可以確定各工件在機器上的加工順序。

2.2 種群初始化

傳統粒子群算法對種群進行初始化時采用隨機策略，但隨機策略面對大規模實際組合優化問題時效果不好，并且會使初始種群中粒子的質量降低。因此，文中采用NEH啟發式算法生成初始種群，該算法假定在所有加工機器上總加工時間大的工件會獲得更高的優先權。具體步驟為：

1)n個工件在加工機器上的加工時間總長按照由大到小的順序進行排列;

2)取前兩個工件調度，使其最大流程時間達到最小;

3)從k=3到n,將第k個工件插入到k個可能的位置,求得最大流程時間。

2.3 粒子尋優操作

粒子速度和位置更新公式為：

vij(t+1)=ωvij(t)+

c1r1(pbestij(t)-xij(t))+

c2r2(gbestij(t)-xij(t))+d,

(5)

xij(t+1)=xij(t)+vij(t+1),

(6)

式中:vij(t)----粒子速度;

xij(t)----粒子位置；

pbestij(t)----粒子的個體最優位置;

gbestij(t)----粒子的群體最優位置；

ω----慣性權重系數；

d----擾動因子；

c1、c2----學習因子；

r1、r2----(0，1)之間的隨機數。

2.4 自適應慣性權重系數

在PSO算法中慣性權重至關重要，它擁有平衡局部勘探和全局勘探的能力。因此，文中采用非線性的、自適應的慣性因子調整方式，迭代開始階段算法在解空間內的尋優能力增強，不容易陷入局部極值，加快算法后期的收斂速度。

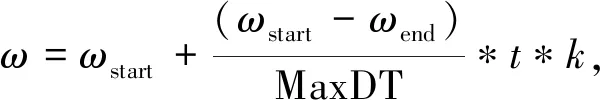
(7)

k=rand+Ε(0.5),

(8)

式中:t----當前迭代次數;

MaxDT----算法允許的最大迭代次數;

Ε(0.5)----平均值為0.5的指數分布;

rand----(0，1)之間的隨機數。

ωstart通常取0.9，這使得在迭代初期算法擁有比較好的勘探能力，能夠擴大搜索范圍。ωend一般取0.4，隨著迭代次數的不斷增加，算法的開發能力逐步增強，這促使粒子加速向全局最佳值逼近。慣性權重ω的曲線如圖1所示。

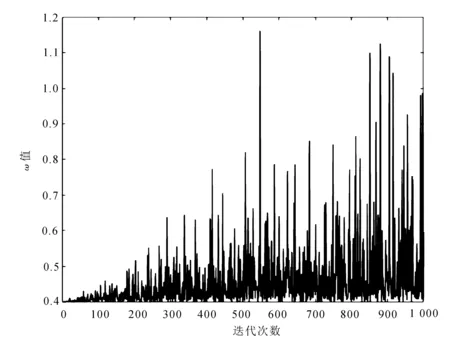
圖1 慣性權重ω的曲線

2.5 擾動因子

經典PSO算法在尋優階段容易陷入局部極值，為此在原速度更新公式中加入了擾動因子d，進而促使粒子在解空間中繼續進行搜索。將擾動因子d設置為一個二進制變量，它取0的概率比較大。當粒子在種群中呈聚集狀態時，擾動因子可以將其打散，防止算法收斂于局部最優值；當種群中的粒子呈分散狀態時，算法受擾動因子的影響較小，可以忽略。

2.6 禁忌搜索

禁忌搜索算法[13](Tabu Search， TS)對局部搜索算法的優化，它能夠避免傳統的局部搜索算法因粒子重復搜索固定區域(方向)而造成粒子收斂于局部極小值。通過建立禁忌表來記錄被禁止的局部極小點，使粒子更新時繞開這些點。并通過破禁準則釋放一些在禁忌表中的點，保證多樣化、有效地探索。

文中引入一種基于位置相似度的禁忌搜索策略[14]，并將它與粒子群算法相結合。對于N維空間中有位置x1=(x11，x12，…，x1N)和位置x2=(x21，x22，…，x2N)，那么位置相似度可表示為λ=N′/N，其中N′為位置x1和位置x2中可行解數值相同的維數。首先建立一個長度為l的禁忌表，用以記錄粒子在搜索過程中所到達的位置。并根據位置相似度閾值更新禁忌表，規則如下：每當粒子抵達全新的位置時，粒子都與禁忌表中的每個記錄做λ計算，超過相似度閾值的位置則被放棄，而小于閾值的粒子所在的位置將加入到當前迭代的候選解隊列中，計算適應度值并更新禁忌表。

2.7 算法流程

采用TIPSO求解FFSP的詳細流程如下：

1)設置算法的基本參數。給定問題規模，迭代次數M，學習因子c1和c2，種群規模N，禁忌表長度。

2)種群初始化，禁忌表初始化。結合NEH算法初始化種群。

3)判斷粒子是否在禁忌表中。若在禁忌表中則執行5)，否則執行4)。

4)更新禁忌表，計算適應度值,并更新個體和種群最優(將目標函數作為適應度評價指標)。

5)利用式(5)、式(6)指導種群中粒子速度以及位置更新。

6)判斷是否達到終止標準。若達到條件，則將最優位置輸出；若不滿足,則重新執行3)。

改進粒子群算法流程如圖2所示。

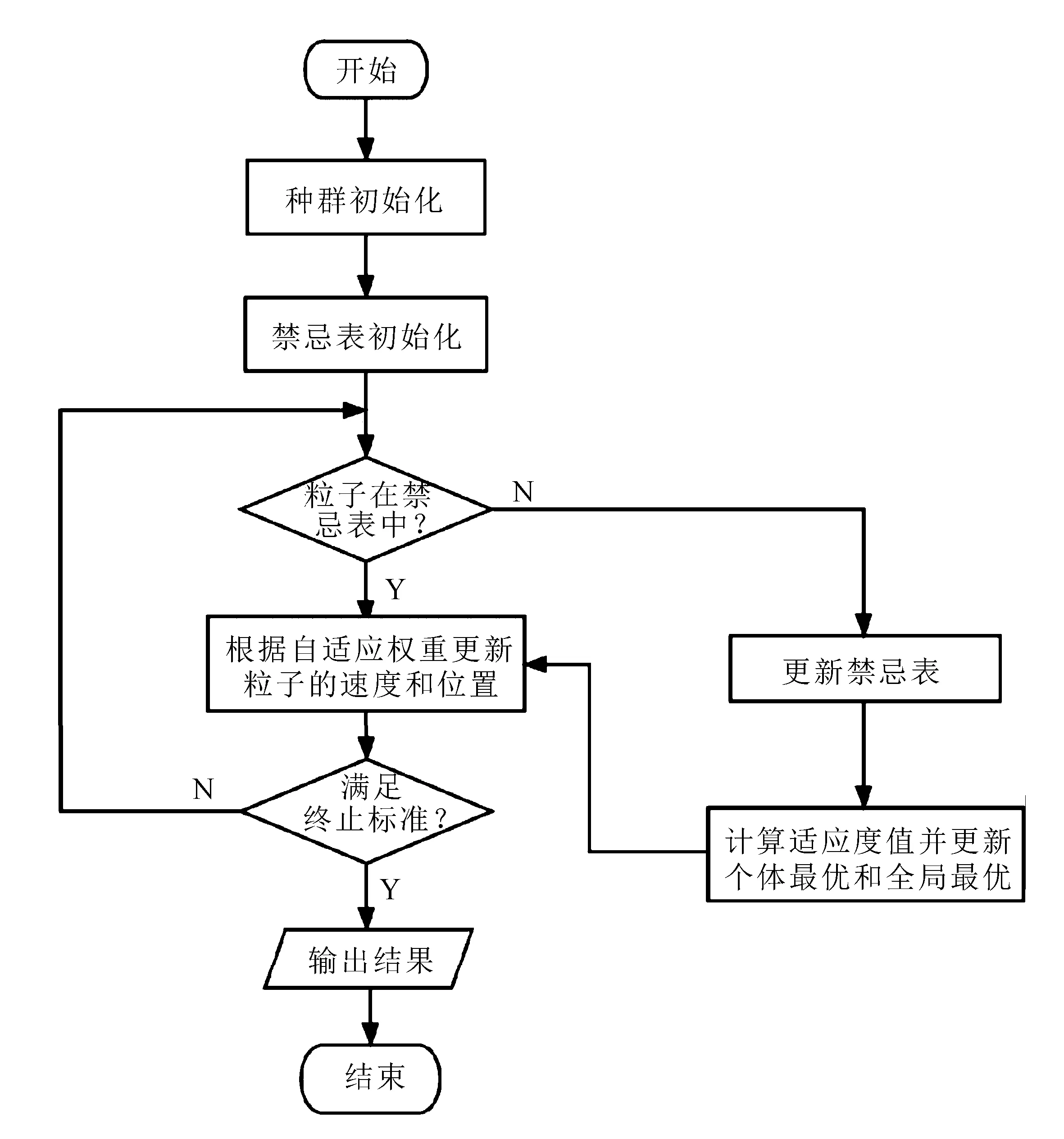
圖2 改進粒子群算法流程

3 仿真結果與分析

為驗證文中提出的改進算法有效性，以Matlab2016a為開發環境，分別使用標準粒子群算法、改進型算法[14]和文中提出的算法在 LA01[15]、FT06[16]、FT10[16]三個不同規模的問題進行了實驗仿真。

算法參數設置如下：粒子個數N=50，LA01、FT06問題規模相對來說比較小，所以最大迭代次數設置為MaxIter=500，FT10問題復雜規模大，其最大迭代次數設置為MaxIter=1 000，學習因子c1=c2=2，ωmin=0.4，ωmax=0.9，禁忌表長度l=2，禁忌閾值η1=0.85，η2=0.95。

TIPSO算法在FT06問題上的最優調度方案如圖3所示。

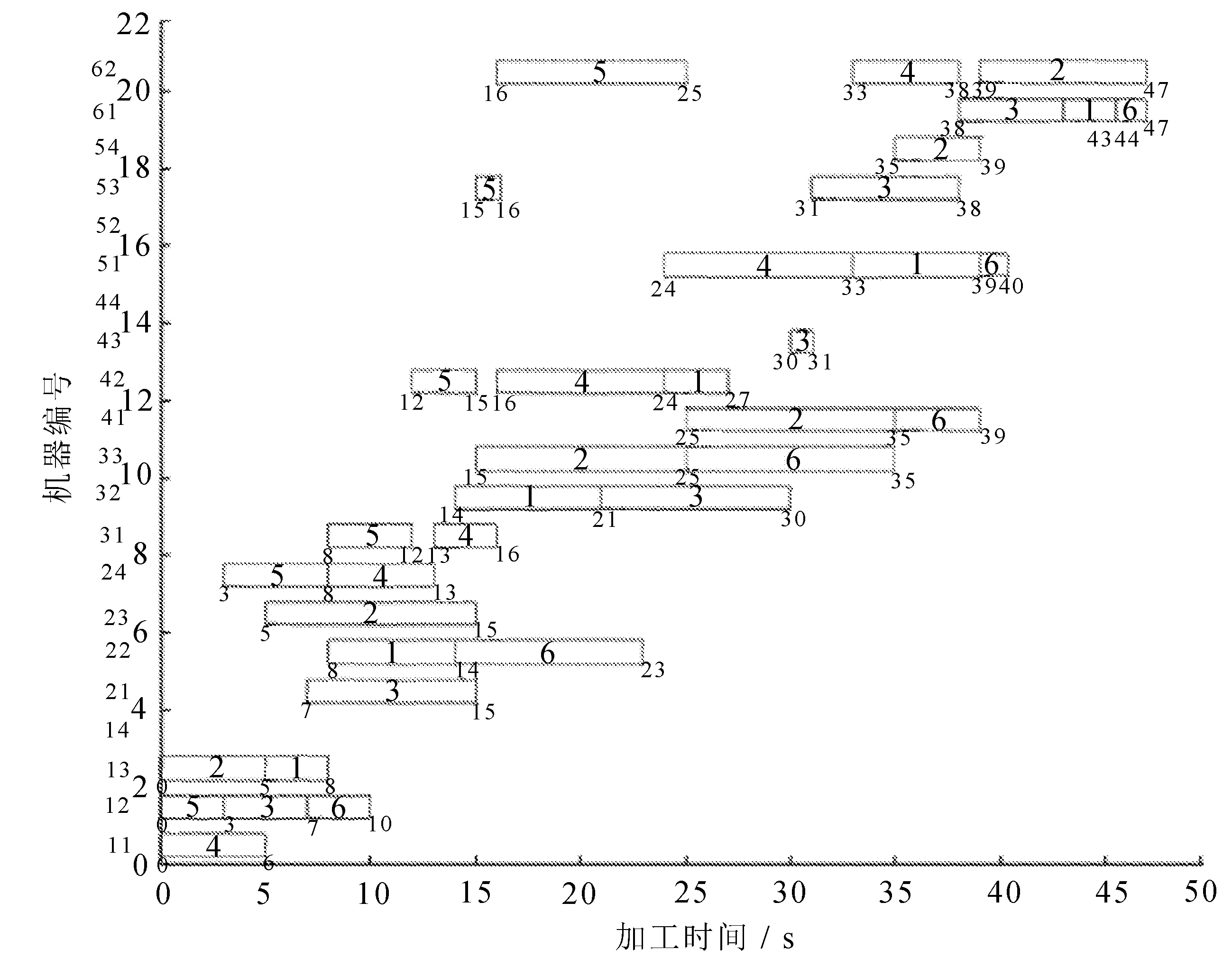
圖3 最優甘特圖

由圖3可知,最短完工時間為47 s。

標準粒子群算法、改進型PSO算法[14]和禁忌粒子群優化算法(TIPSO)求解FT06基準算例、LA01基準算例、FT10基準算例的收斂結果對比圖，分別如圖4～圖6所示。

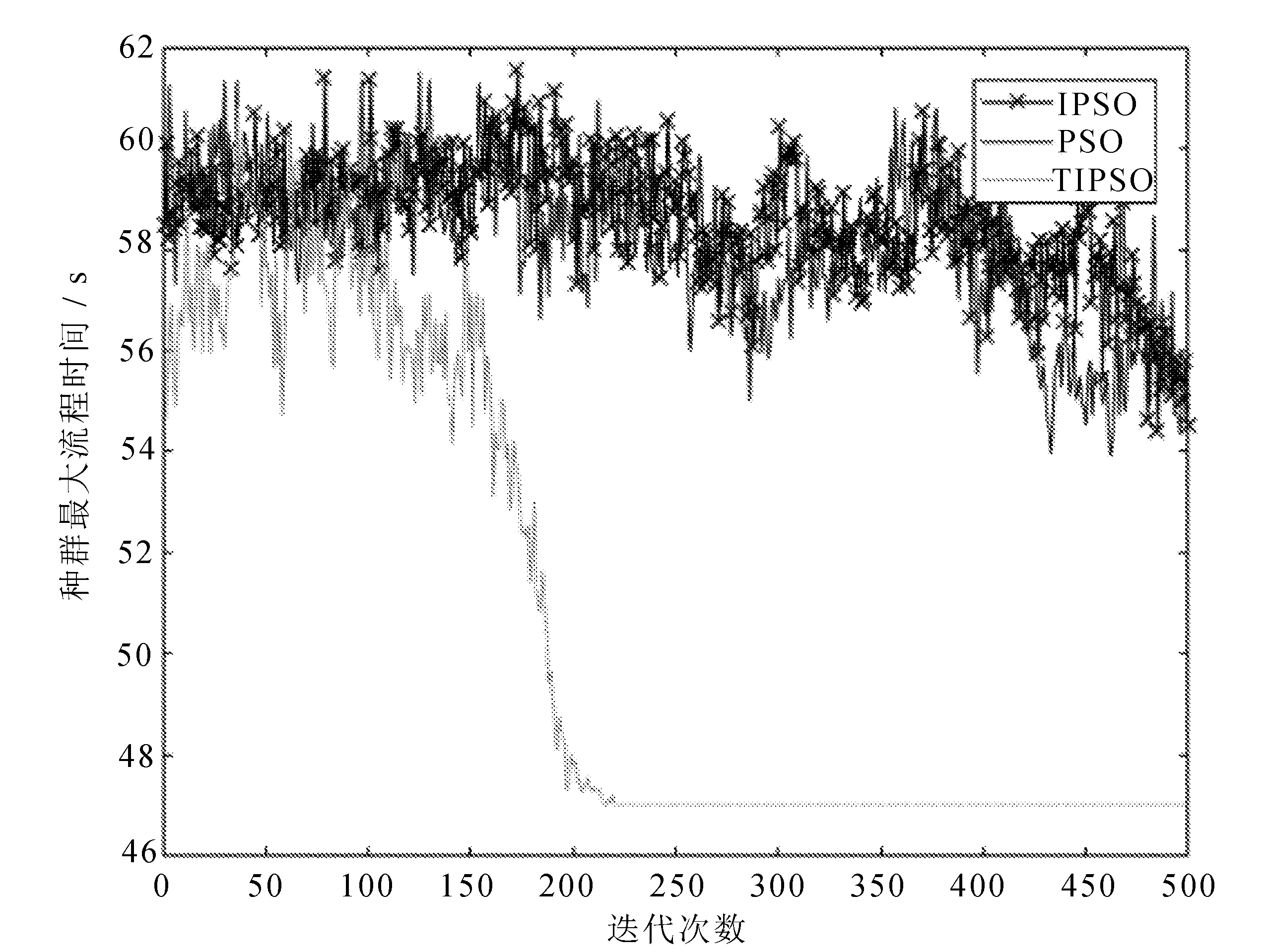
圖4 收斂速度對比圖(FT06)

圖5 收斂速度對比圖(LA01)

圖6 收斂速度對比圖(FT10)

由上圖可知，TIPSO可以求出FT06算例的最優解47、LA01算例的最優解453和FT10算例的最優解706，其他兩種算法均找不到最優解。在搜索后期TIPSO得到的種群最大流程時間比較短，說明TIPSO算法具有較優的收斂性能，而且TIPSO算法在面對大規模問題時表現依然良好。這是因為TIPSO 算法結合禁忌搜索策略對種群的初始化、權重因子進行了改進，保證了算法初始種群的多樣性，更接近全局最優解，并且收斂效率也更好，而擾動因子的引入能夠幫助跳出局部最優解，繼續在解空間內進行搜索。

4 結 語

設計了一種禁忌粒子群優化算法，在求解FFSP問題時表現出良好的性能。將基于位置相似度的禁忌策略和粒子群算法結合起來，自適應慣性權重因子和擾動因子的加入，可以有效地避免粒子過早收斂的情況，幫助粒子提高其全局搜索能力，同時將NEH 啟發式算法引入種群的初始化中，提高了粒子種群的多樣性，可以幫助算法在較短時間內收斂于最優解。最后通過仿真實驗證明了該算法的可行性與有效性。