分布式協(xié)同干擾對防空雷達的壓制效能仿真

蔣東旭，蔣路華，謝登召

(中國船舶集團有限公司第八研究院，江蘇 揚州 225101)

0 引 言

防空雷達作為空中信息情報獲取的重要手段，承擔著對來襲空中威脅的探測、跟蹤、目標識別和火力引導等任務(wù)，在國土防御中扮演著重要角色[1-3]。隨著電子信息技術(shù)的發(fā)展，防空雷達抗干擾水平不斷提高，傳統(tǒng)的電子干擾手段已很難對其取得理想的干擾效果[4-6]。在此背景下，分布式協(xié)同干擾應(yīng)運而生。分布式協(xié)同干擾是以有人、無人平臺為載體，通過掛載不同的任務(wù)載荷而發(fā)展起來的一種新型作戰(zhàn)樣式[7-8]。其中無人平臺由于雷達截面積(RCS)小，因此可飛抵敵方縱深，實施抵近干擾，從而掩護有人平臺遂行作戰(zhàn)任務(wù)。分布式協(xié)同干擾不僅可以大幅提升干擾效能，而且在干擾敵方雷達的同時不會影響己方其他設(shè)備的正常工作。

目前，對防空雷達的分布式干擾，程彥杰等人[9]通過仿真計算，研究了不同配置情況下的探測威力和暴露區(qū)，得出了不同干擾條件下雷達探測區(qū)域的變化和特點。于家傲等人[10]研究了不同干擾無人機編隊對預警機探測效能的影響，周武等人[11]研究了無人機掩護突防時對雷達的分布式干擾策略。這些研究對于分布式干擾壓制區(qū)的計算均采用簡單的疊加，而對于集群作戰(zhàn)下的分布式協(xié)同干擾，這種方法往往是不適用的。盡管何俊等人[12]研究了對機載轟瞄雷達的多站協(xié)同干擾壓制區(qū)的計算，但文章針對的是要地防空作戰(zhàn)背景下對來襲飛機的干擾，數(shù)學模型不適用于多機協(xié)同對敵防空雷達的干擾。

針對上述問題，本文開展了分布式協(xié)同干擾對防空雷達的壓制效能研究，從分布式干擾的數(shù)學模型出發(fā)，建立了基于空間功率合成理論的分布式協(xié)同干擾方程，并在此基礎(chǔ)上進行數(shù)值仿真，對壓制效能進行分析研究。

1 分布式干擾下的干擾建模

為了便于分析建模，先建立如圖1所示的單干擾機干擾防空雷達示意圖[13]。

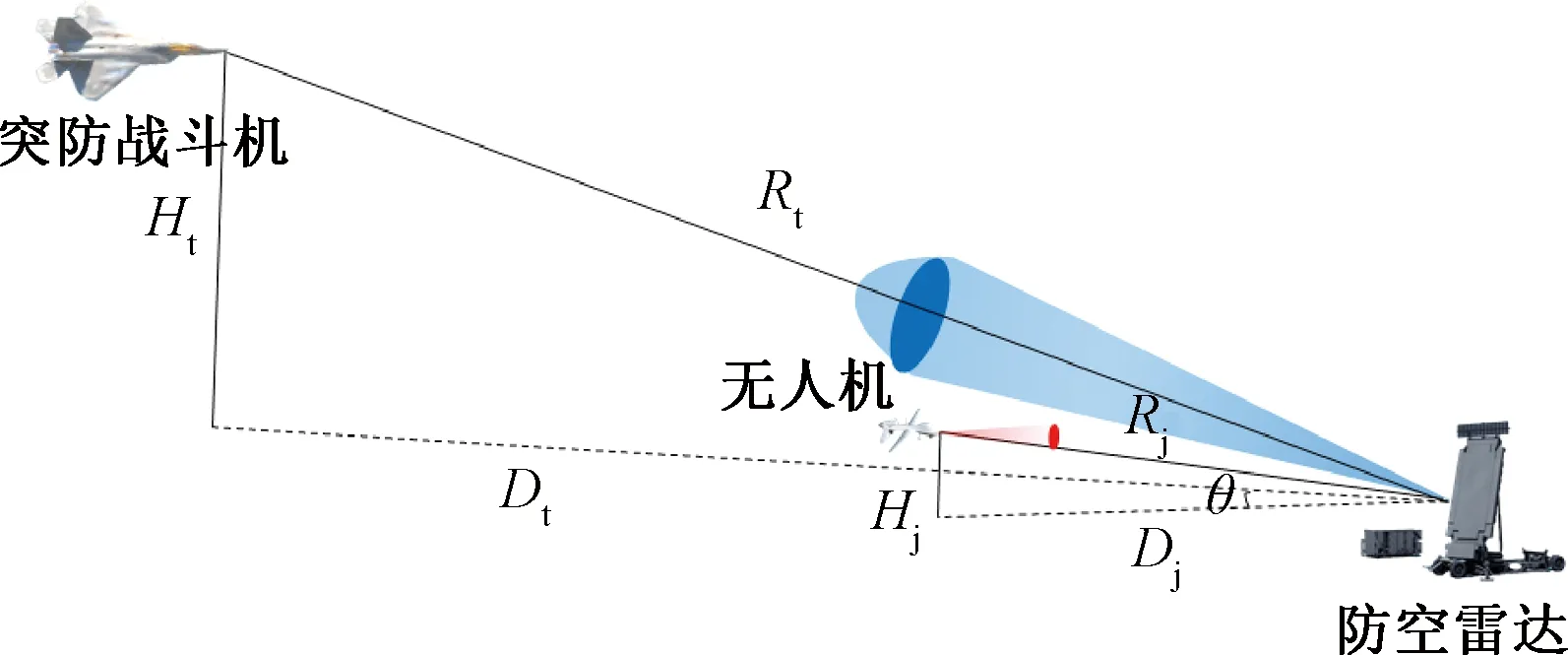
圖1 單干擾機干擾防空雷達示意圖

載有干擾機的無人機與雷達的直線距離為Rj，水平距離為Dj，飛行高度為Hj，突防飛機與雷達直線距離為Rt，水平距離為Dt，飛行高度為Ht。當防空雷達天線主瓣對準目標探測時,到達雷達接收機的有用目標信號功率Prs為[14]：

(1)

式中：Pt為雷達發(fā)射功率；Gt為雷達天線發(fā)射增益；Gr為雷達天線接收增益；λ為雷達發(fā)射電磁波波長；σ為目標反射截面積；Lr為雷達系統(tǒng)損耗。

進入雷達接收機的干擾信號功率Prj為：

(2)

式中：Pj為干擾機發(fā)射功率；Gj為干擾天線發(fā)射增益；Gr(θ)為干擾機方向上雷達天線接收增益；γ為干擾信號與雷達系統(tǒng)極化失配引起的損耗；Lj為干擾信號在干擾機和進入雷達內(nèi)部后的射頻傳播損耗；Δfr為雷達接收機帶寬；Δfj為干擾信號帶寬。

根據(jù)干擾方程可以得到：

(3)

式中：Kj為壓制系數(shù)。

因此可以得到壓制距離計算公式如下：

(4)

式中：Gr(θ)是雷達在干擾機方向上偏轉(zhuǎn)θ角度的增益。

根據(jù)上式可以求出壓制區(qū)域。

對于如圖2所示的由多個無人機群實施的分布式干擾，這些無人機在空中采用半圓弧型布陣，并且通信和信號同步滿足要求。結(jié)合上述建模，可以得到n部干擾機(信號互不相關(guān))分布式干擾的干擾方程為：

(5)

通過上式可以得到n部干擾機(信號互不相關(guān))的分布式干擾壓制區(qū)。

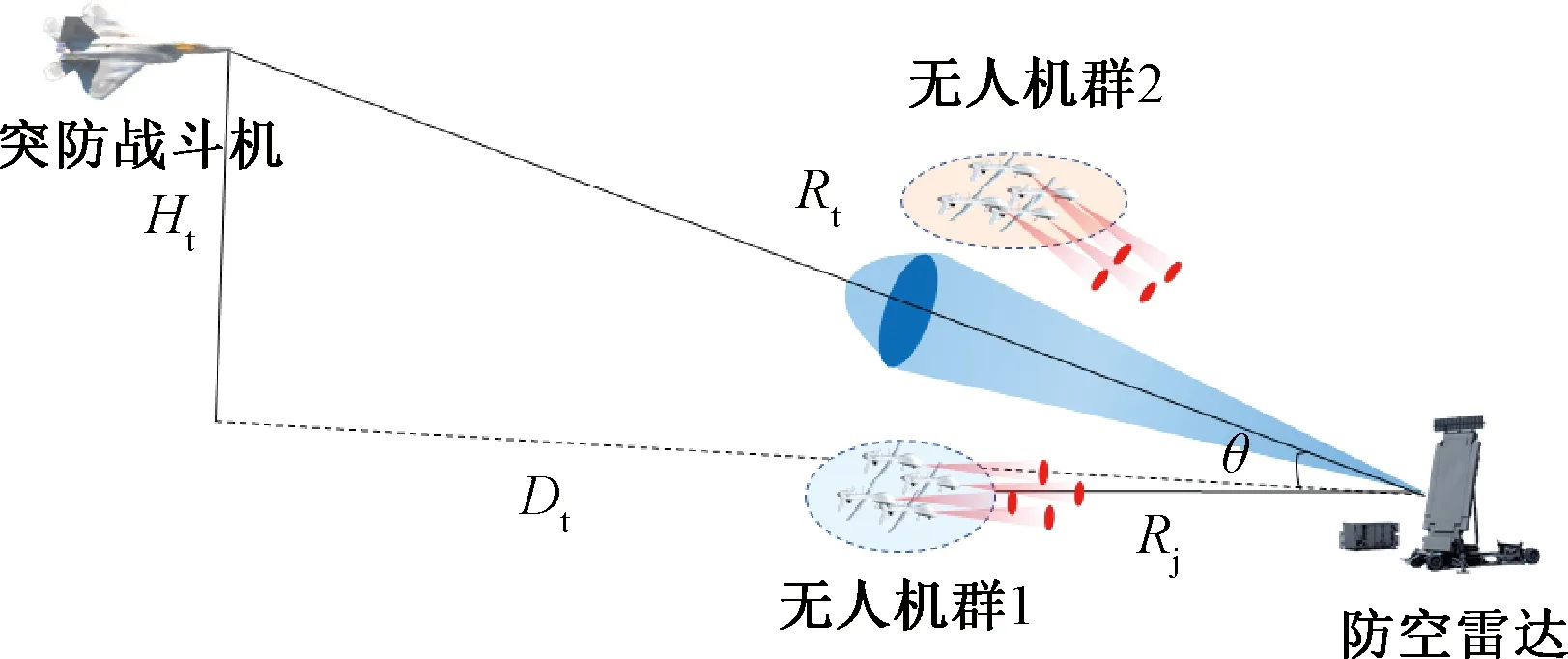
圖2 對防空雷達的分布式干擾示意圖

2 分布式協(xié)同干擾下的干擾建模

在分布式干擾時，通過控制各干擾信號的相位關(guān)系，可以獲得分布式協(xié)同干擾的信號空間功率合成，使各干擾信號在預定的交叉區(qū)域合成足夠強的功率。因此，分布式協(xié)同干擾下的有效壓制區(qū)的計算不宜采用簡單的直接疊加法。為此，對上一節(jié)的建模過程進行優(yōu)化，首先基于空間功率合成理論計算多干擾站在防空雷達處的合成功率，然后給出分布式協(xié)同干擾的整體干擾方程，最后根據(jù)該干擾方程求得分布式協(xié)同干擾的有效壓制區(qū)。

設(shè)防空雷達共接收到M個干擾機發(fā)射的干擾信號，第i(i=1,2,…,M)個干擾機的干擾信號可寫成用其幅度與相位表示的一般形式，具體表達式為：

(6)

式中：φi為第i個干擾信號到達機載轟瞄雷達處的相位。

可得其到達機載轟瞄雷達處的信號功率為|Xi|2=Pri，則此時合成信號的形式為：

(7)

則合成信號功率為：

(8)

當|φi-φj|=0時，得到最大的信號合成功率，其表達式為：

(9)

當各干擾站到達功率相等時，即Pri=Prj，上式為：

(10)

因此，在分布式干擾時，信號合成功率最大可為單干擾機干擾功率的M2，其中M為參與合成的干擾機數(shù)量。

通常無人機集群由于受通信間距的限制，各無人機之間的距離較小，相對于其與防空雷達的距離基本可以忽略不計，為此，每個無人機集群可以被看做一個整體進行考慮。對于有L個無人機集群，每個無人機集群內(nèi)部無人機數(shù)量為M，則可以得到分布式協(xié)同干擾下的干擾壓制區(qū)：

(11)

式中：P′ji為M架無人機集群的合成功率。

3 分布式協(xié)同干擾下的數(shù)值仿真

根據(jù)上述理論分析，在對被突防戰(zhàn)斗機、防空雷達和無人干擾機各項參數(shù)設(shè)置的基礎(chǔ)上開展數(shù)值仿真，參數(shù)取值如下：Pt=300 kW，Gt=Gr=35 dB，每個無人機群內(nèi)部無人機的取值根據(jù)任務(wù)需求和干擾任務(wù)載荷能力來選，本文取值為10，這些無人機的干擾載荷完全相同，也即發(fā)射功率和天線增益一樣，其中Pj=2 W，Gj=10 dB；戰(zhàn)斗機的RCS為σ=5 m，考慮常規(guī)的壓制干擾，因此壓制系數(shù)Kj取6 dB，忽略其他損耗等帶來的影響，Gr(θ)以某防空雷達方向圖的擬合方向圖進行，其方向圖如圖3所示。

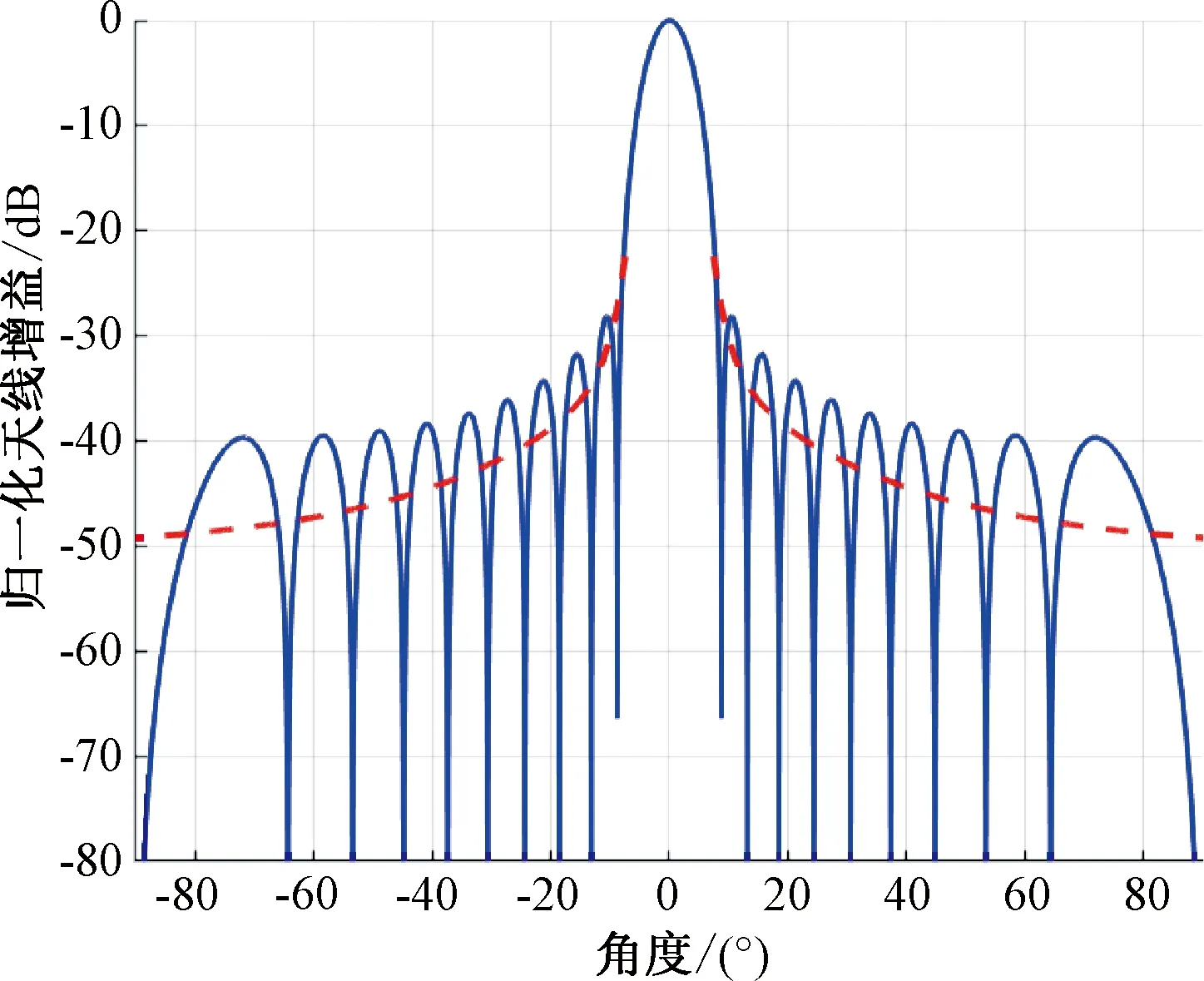
圖3 某雷達天線方向圖及其擬合

圖4～圖6分別為單個無人機群、2個無人機群和3個無人機群的分布式協(xié)同干擾前后的壓制區(qū)。其中單個無人機群位于0°處，Rj為30 km;2個無人機群情況下，無人機分別位于±10°處，Rj均為30 km；3個無人機群情況下，無人機分別位于0°和±10°處。

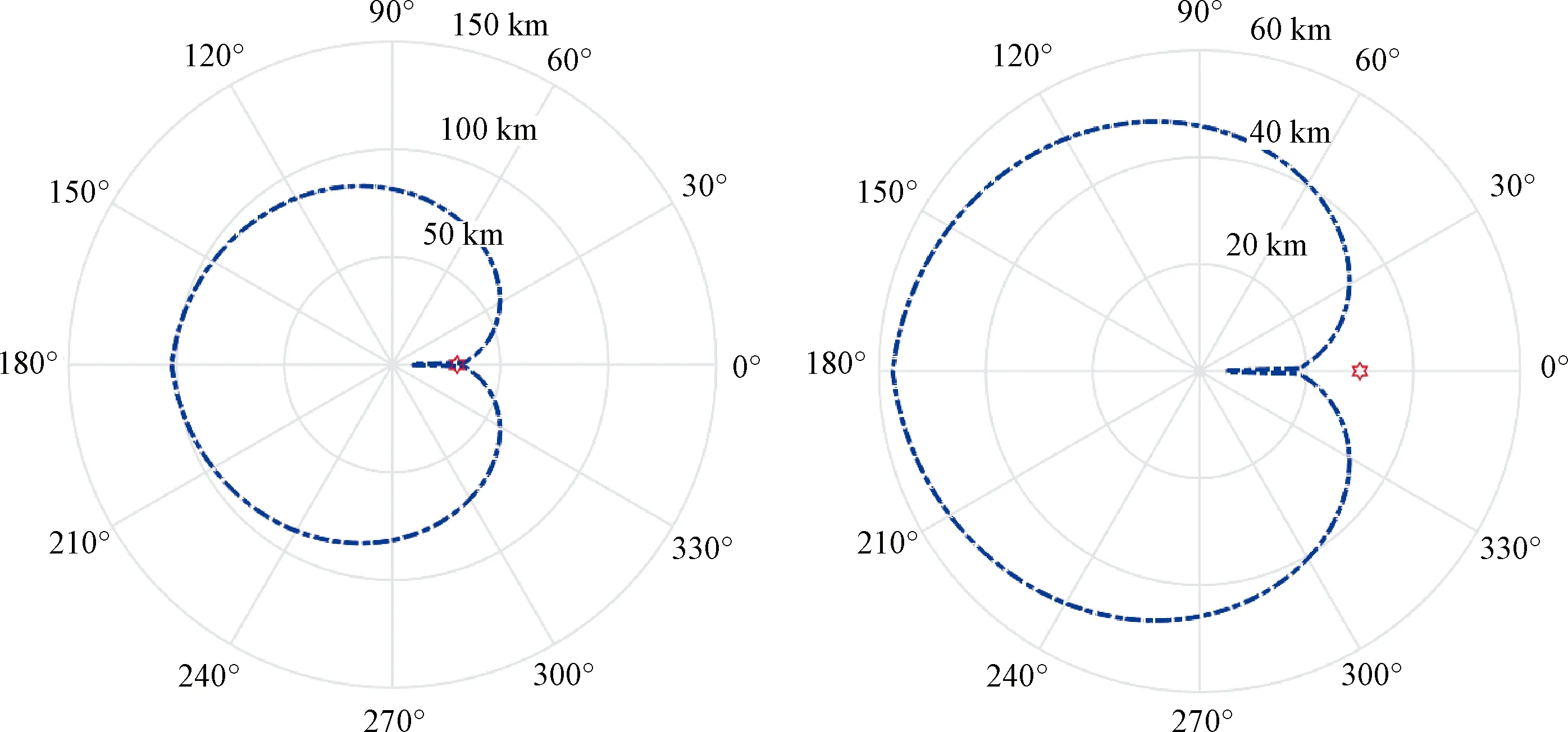
圖4 單個無人機群分布式協(xié)同干擾前后的壓制區(qū)

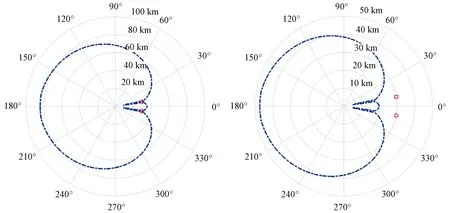
圖5 2個無人機群分布式協(xié)同干擾前后的壓制區(qū)

圖6 3個無人機群分布式協(xié)同干擾前后的壓制區(qū)

由圖4～圖6可以看出，在采用分布式協(xié)同干擾前，單個無人機群干擾的壓制區(qū)邊界為100 km。隨著干擾機群數(shù)目的增加，雷達的燒穿距離逐漸縮小。當干擾機群為3個時，雷達的燒穿距離小于80 km。當這些無人機群的干擾通過協(xié)同實現(xiàn)空間功率合成，單個無人機群干擾的壓制區(qū)邊界縮小至57.4 km。而3個無人機群分布式協(xié)同干擾下的壓制區(qū)邊界為43.4 km，并且隨著干擾機群數(shù)目增多，干擾扇區(qū)也越來越大。為此，在對防空雷達進行干擾時，可以通過無人機群的干擾協(xié)同降低對單平臺任務(wù)載荷的功率需求。

圖7為不同干擾角度對防空雷達壓制區(qū)的影響，選取的角度分為為：0°與±5°、0°與±15°和0°與±25°。

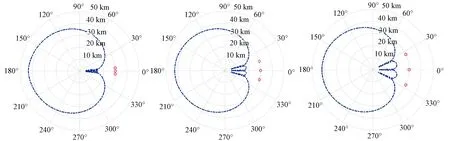
圖7 不同干擾角度對防空雷達壓制區(qū)的影響

由圖7可以看出，隨著無人機群與雷達之間夾角的增大，干擾扇區(qū)會逐漸增大，從最初的不到10°增大至30°；但也會帶來扇區(qū)內(nèi)雷達燒穿距離的變大，從最初的15 km增大至20 km。干擾扇區(qū)的增大有利于突防飛機的掩護，但雷達燒穿距離的增大將不利于掩護干擾機的突防。因此在實際作戰(zhàn)時，需要根據(jù)突防任務(wù)的具體情況，合理部署無人干擾機用以獲得最優(yōu)的干擾掩護區(qū)。

4 結(jié)束語

本文針對分布式協(xié)同干擾計算模型過于簡單、無法適應(yīng)當前協(xié)同作戰(zhàn)的效能分析，提出基于空間功率合成理論的分布式協(xié)同干擾，并對其進行了理論建模和數(shù)值仿真。仿真結(jié)果表明，對于單個無人機群，協(xié)同前干擾的壓制區(qū)邊界為100 km；而通過協(xié)同后，壓制區(qū)邊界縮小至57.4 km，并且增大干擾機群之間的夾角，干擾扇區(qū)隨之增大。文章內(nèi)容對于未來協(xié)同突防的研究具有重要意義。